基于光电编码器的永磁球形电动机转子方位测量系统*

吴凤英， 魏章波， 席金强

(天津理工大学 天津市复杂控制理论与应用重点实验室，天津 300384)

0 引 言

球形转子的方位参数是构成永磁球形电动机[1]姿态、速度和转矩闭环控制系统的重要组成部分。目前解决球形转子方位测量问题的方法主要有基于非接触光电测量原理的图像处理法、基于磁场分布的霍尔元件、基于机械连接的测量方法[2]。图像处理方法需要在球形转子表面绘制图形，同时需要较高的计算能力要求，测量周期长[3]。霍尔元件方法需要对球形转子形成的磁场分布有准确的模型，同时也需要进行相关计算[4]。基于机械连接的方法测量简单，速度快，但测量装置需要附件连接转子输出轴，结构较为复杂[5]。

本文以三自由度永磁直流球形电动机为研究对象，利用3个增量式光电编码器组合测量的方式，通过硬件电路实现对脉冲的倍频、鉴相、可逆计数和存储，将计数值以串行方式传输到单片机，计算出表示转子方位的欧拉角后，由串口发送到电机闭环控制系统中作为反馈信号，并在液晶显示器(liquid crystal display,LCD)上实时显示。系统试验得到表示球形转子方位的欧拉角参数，分析了该系统的性能，并对系统测量结果进行验证。

1 永磁球形电动机结构

球形转子方位测量装置的机械结构中，采用O型框作为平衡框的外框，采用C型框作为平衡框的中框，采用球形转子作为内框， O型框可以绕安装支座旋转；C型框可以绕O型框正交轴旋转；转子可以绕C型框正交轴旋转。

三个光电编码器分别安装在支座与O型框连接处、O型框与C型框连接处和C型框与转子输出轴处。

2 系统设计

2.1 系统整体设计

系统采用3个光电编码器组合测量三自由度球形电机转子方位，系统整体结构框图如图1所示。

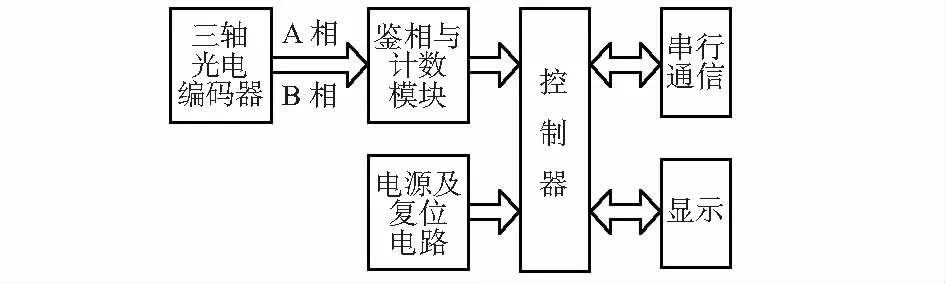
图1 系统整体结构框图

设计的方位数据参数必须经过光电编码器检测、倍频、鉴相、可逆计数、数据转换和存储、显示、串口传输等过程，数据处理过程中，为了实现系统较高的实时性和可靠性，倍频、鉴相、可逆计数、数据转换和存储过程易于硬件实现，而显示和串口传输过程较为复杂，所以用软件方法[6]实现。

2.2 硬件设计

系统整体硬件框图如图2所示。加减计数电路用3片74HC193级联组成，其工作的条件是CU和CD中一个输入脉冲时，另一个必须为高电平。而编码器输出的A,B 2路脉冲不能直接输入到计数器，所以,对这2路脉冲先进行鉴相，同时通过鉴相电路也可以判断出电机的正转和反转。鉴相电路用1个D触发器和2个与非门组成，同时将光电编码器产生的A,B 2相脉冲经过异或门逻辑可使编码器测量精度提高2倍。考虑到1个编码器计数电路就有12路输出，3路同时工作导致单片机I/O口数量不够，所以,采用并行输入串行输出芯片(74HC165)，3路12位数据被锁存并以串行方式传输到单片机，同时降低了硬件复杂度。

图2 系统整体硬件框图

2.3 软件设计

软件是在Keil开发环境下采用C语言完成的，此程序主要实现初始化、数据锁存、计算欧拉角、显示和传输数据等功能。采用3个定时器中断设定1 s标志位采集3路计数脉冲，计算出欧拉角后在LCD12864液晶上显示出测量结果。同时通过RS—232串口把测量到的球形电机方位数据发送到计算机，由计算机完成球形电机的闭环控制。

3 系统性能分析

3.1 球体方位描述方法

本系统采用物理连接的方法检测球形转子的方位参数，即用现有的方位测量传感器来测量，而参数越多，所需要的传感器数量也会增加。所以，从实用性方面考虑，采用较少参数的欧拉角描述法表达永磁球形电机的转子方位的基本物理参数。

永磁球形电动机的球形转子具有刚体属性，根据欧拉旋转理论，空间刚体的任何一次姿态变化，都可以用绕运动刚体自身坐标系或者参考坐标系坐标轴的3次旋转复合而成[7]。因此，刚体的姿态可以用3个角度唯一描述。欧拉角表示法中的zyx型利用3个独立角度参量描述了球形转子绕坐标系3个正交轴旋转的运动。采用这种欧拉角表示法可以采用3只角度传感器分别测量3个正交轴方向的角度，故本设计采用zyx型欧拉角描述球形转子的方位。zyx型欧拉角坐标系转换示意图如图3所示。

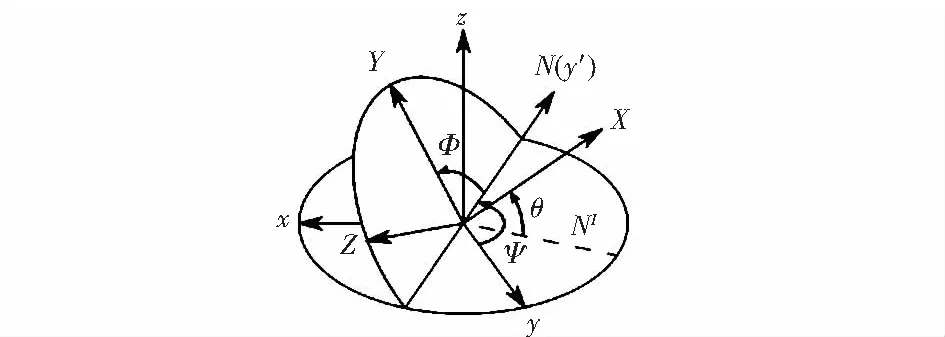
图3 zyx型欧拉角坐标转换示意

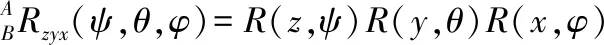
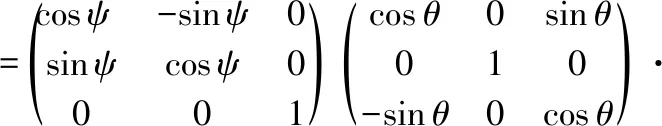
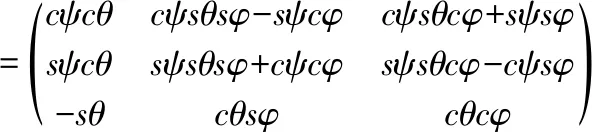
式中s=sin,c=cos，下文中也按照此规定表示。角度ψ,θ,φ为表示转子方位的广义欧拉角。

3.2 误差模型

依靠3个光电编码器组合测量转子方位时，测量数据往往会有微小的方位测量误差存在，这些误差可由微分变化来表达。在定子坐标系{T}绕矢量f的微分旋转dθ的变化表示为Rot(f-dθ)，则用微分旋转表示微分变化T+dT=[Rot(f-dθ)]T，即

dT=[Rot(f-dθ)-I]T=Δ·T

(1)

Δ=[Rot(f-dθ)-I]

(2)

式中T为齐次变换矩阵，I为单位矩阵，Δ为对定子坐标系的微分旋转变换矩阵。

绕矢量f的微分旋转dθ等价于分别绕x轴、y轴和z轴的微分旋转δx,δy和δz。计算式(2)，得

(3)

3个光电编码器组合测量误差对球形转子方位测量精度的影响本质上是转子坐标系内的微分运动，设理想状态下的球形转子方位是余弦矩阵R，实际测量得到的球形转子方位是Ts，则由误差矩阵TΔ来描述

TΔ=Ts-R

(4)

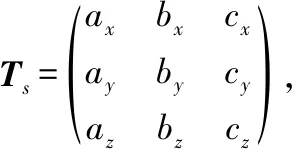
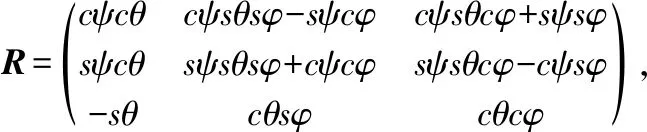
ax=cψcθ+(cψsθsφ-sψcφ)δz-(cψsθcφ-sψsφ)δy

ay=sψcθ+(sψsθsφ+cψcφ)δz-(sψsθcφ-cψsφ)δy

az=-sθ+cθsφδz-cθcφδy

bx=cψsθsφ-(sψcφ-cψcθ)δz+(cψsθcφ+sψsφ)δx

by=sψsθsφ+(cψcφ-sψcφ)δz+(sψsθcφ-cψsφ)δx

bz=cθsφ+sθδz+cθcφδx

cx=cψsθcφ+(sψsφ-cψcθ)δy-(cψsθsφ-sψcφ)δx

cy=sψsθcφ-(cψsφ-sψcθ)δy-(sψsθsφ+cψcφ)δx

cz=cθcφ+sθδy-cθsφδx

3.3 性能参数

1)测量范围：该测量系统由于受机械壳体的限制，转子输出轴绕整个圆周360°自旋运动和20°范围内的侧倾运动，故欧拉角ψ,θ,φ的测量范围分别为：-360°≤ψ≤360°,-20°≤φ≤20°,-20≤θ≤20°。

2)线性度：因为3只光电编码器安装在球形转子的输出轴，与电机同轴转动，所以，该测量系统欧拉角的输入与输出成线性关系。

3)分辨率：设3只光电编码器转动一圈输出的脉冲个数分别为N1，N2和N3，且硬件电路实现了二倍频设计，所以，A，B，C 3个光电编码器的输出分辨率分别表示为RA=2π/2N1,RB=2π/2N2,RC=2π/2N3。

4 实验验证

在本系统中，考虑到传输过程需要处理的数据量少，且运算简单，指令条数不多，不需要处理能力突出的处理器，故采用STC12C5A60S2单片机。

由于本系统中的永磁球形电机最高设计转速为500 r/min，且选用了12 MHz频率的晶振，因此，光电编码器响应频率应大于2 048×500/60=17.06 kHz，外部输入计数脉冲的最高频率为12×1 000/24=500 kHz。同时该球形电机的结构限制了编码器的结构尺寸，只用于实验室环境，所以，采用2个半空心轴编码器ZKP3808—001G—1024—BZ3—5L和1个全空心轴编码器IHA6012—008G—1024BZ3—5L。3个编码器均为1 024脉冲差分输出，频率响应100 kHz，最大转速3 000 r/min，且接线表相同。

测试1ψ,θ,φ分别单独变化情况下的测试。

测试2ψ,θ,φ2个角度组合变化情况下的测试。

测试3ψ,θ,φ3个角度同时变化情况下的测试。

由于自转角输出轴法兰和O型机械框架固定激光测距仪较为方便，故ψ和θ的实际角度由激光测距仪测量得到，O型机械框架对应的角度φ由量角器测量所得，整个验证实验装置如图4所示。

图4 球形转子测量系统

所有的实验都从零位标定开始，将激光测距仪放置在O型框上，调整机械框架使测距仪显示0°，即O型框处于水平位置。再通过量角器或直角尺使C型框处于90°位置，即O型框架和C型框架处于正交的状态。此时即为零位状态，零位标定完成。

激光测距仪测试距离为0～40 m，内置电子角度传感器，角θ便可直接测量，角ψ则通过测量随转子输出轴自转后在实验室墙面扫过的直线距离与激光长度计算得到。由于实验室条件限制，只能验证90°以内的自转角ψ，且激光长度为10.00 m。将验证实验测量数据记为标准值，编码器测量数据记为测量值，每种类型数据连续测量10次后取算术平均值，所有的测试内容和每个参数的最大测量误差如表1所示。

表1 验证实验测量数据及误差

由表中测量最大误差可以看出，对于测试1，在测试范围内，欧拉角θ,φ的测试结果比欧拉角ψ的测试结果更精确。在测试2中，最大测量误差表明ψ,θ,φ两两组合变化的测量是彼此独立的。在测试3中，欧拉角ψ,θ,φ同时变化时，3个欧拉角的测量误差在合理的范围内。

将测距仪放置在电机法兰处，轻调转子输出轴，当LCD上的角度跳变1°，测量激光在10 m处墙面扫过的距离为0.127 m，代入弧长公式即可近似计算出测量系统测量到电机转动1°时，实际则转动1.36°，测量结果较为准确。

5 结束语

设计了一种基于3个光电编码器组合测量的永磁球形电动机转子方位测量系统，经实验验证表明：该方法不仅电路简单，而且实现了较高的精度，可靠有效，既为下一步实现永磁球形电机闭环控制奠定了基础，又与非接触测量方法的测量结果进行对比，为相关的方法提供有效的验证手段。