多元主体下有源配电网规划方案协同评估研究

冯磊

（云南电网有限责任公司电网规划建设研究中心，昆明 650011）

0 前言

随着电力市场的发展，配电网规划愈渐成为复杂的非线性决策过程，与此同时分布式电源、储能、电动汽车的接入使得传统配电网逐步向有源配电网转变，配电网规划中涉及的各投资主体都对规划方案提出了更高的要求，如何综合各方利益对有源配电网规划方案进行科学全面的评估成为当前亟需解决的问题。

目前，国内外已有一些对于有源配电网可靠性以及环境效益的评估研究成果报道。文献[1]在计及分布式发电效益成本的基础上，构建了考虑节能减排指标的主动配电网低碳优化模型。文献[2-3]分别使用序贯蒙特卡洛模拟法、点估计法对含分布式电源的主动配电网进行可靠性评估。文献[4]综合考虑配电公司与分布式电源投资商的利益，构建了主动配电网多目标规划模型。文献[5-6]分别针对终端电力用户和电网企业，从安全性、优质性和高效性等方面对双方需求进行了探讨，构建了反映智能电网体系中用户需求和电网企业需求的评估指标体系，但未考虑环境效益指标及设备投资主体。文献[7]计及了用户参与度对主动配电网经济价值的影响，结合技术及经济指标对主动配电网实际案例进行了协调评估。文献[8]构建了含分布式电源的城市配电网规划方案评价指标体系，采用层次分析法对方案进行综合评价，但未考虑参与投资的多利益主体。以往配电网规划方案评估研究主要集中于采用合适评估方法协助同一利益主体获取综合最优的规划方案，如层次分析法[9]、熵权法[10]、逼近理想点法[11]、数据包络法[12]等，鲜少有计及电力市场环境下多利益主体进行协同评估的研究。

本文建立了有源配电网规划方案评价指标体系，并对有源配电网规划过程涉及的各利益主体进行了指标划分。针对单个主体，采用带有层次分析法（Analytic Hierarchy Process,AHP）约束锥的超效率数据包络线（Super-Efficiency Data Envelopment Analysis, SEDEA）交叉评估法进行方案的优选排序；针对多元主体，建立了基于满意度和一致性的专家权重优化模型。最后以我国某地有源配电网三种待选规划方案为例对本文所构建的指标体系及评估方法进行验证分析。

1 有源配电网规划评价指标体系

根据有源配电网的技术特性以及相关部门对电网规划、运行性能的要求[13]，从可靠性、安全性、经济性及技术发展性等方面建立有源配电网规划方案评价指标体系。

1.1 评价指标体系构建

结合传统配电网规划评估指标，将有源配电网规划方案评价指标集划分为可靠性、安全性、经济性及技术发展性四类，其中技术发展性指标包含环境及用户类指标。构建有源配电网规划方案评价指标体系如图1所示。

图1 有源配电网规划方案评估指标集

考虑到有源配电网规划过程中涉及多利益方，将投资主体划分为四类：配电企业、DG投资商(Distributed Generation Owner,DGO)、EES投资商(Electrical Energy Storage Owner,EESO)以及需求侧集成服务商(Demand Response Aggregator,DRA)。根据参与投资的不同主体对图1中的指标集进行划分，得到考虑不同利益主体的有源配电网规划方案评价指标体系，如图2所示。

图2 考虑多元利益主体的有源配电网评价指标体系

1.2 评价指标计算方法

基于建立的有源配电网规划方案评价指标体系，对诸如系统平均停电频率、停电持续时间等传统评价指标和分布式电源渗透率、低碳收益等技术发展性指标进行计算。

1.2.1 传统评价指标

1.2.1.1 可靠性指标

采用系统平均停电频率、系统平均停电持续时间及系统供电可靠率衡量系统供电可靠性水平。具体计算公式参考文献[14]。

采用重要负荷供电可靠率、重要负荷缺供电量指标衡量负荷可靠性水平：

1）重要负荷供电可靠率SAIUIg

规定时间内重要负荷节点g的有效供电总时间与要求的总供电小时数之比：

式中：ug为负荷点g的平均停电持续时间（h/年）DG/EES接入点供电可靠率SAIUIdg/SAIUIees与SAIUIg计算原理类似，篇幅限制不再具体讨论。

2）重要负荷缺供电量CAIDIg

规定时间内由于系统故障而使重要负荷节点g损失的电量：

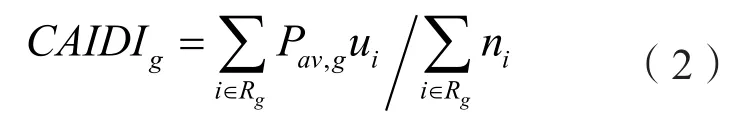
式中：Rg为重要负荷节点g的位置集合；Pav,g为重要负荷节点g的平均负荷值(kW).ni为负荷节点i的用户数。

参考文献[14]中基于对偶抽样蒙特卡罗法计算含DG的主动配电网的可靠性指标。

1.2.1.2 安全性指标

1）系统整体安全性指数ISI

结合文献[15]中对配电网安全性指标的分析，提出系统整体安全性指数ISI。通过计算系统在“N-1”条件下不同重要程度负荷的转移率来定量评价有源配电网整体的供电安全性水平。

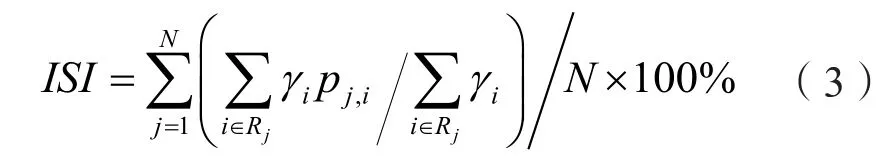
式中：N为系统中可能会发生故障的元件总数；Rj为第j个元件故障影响的负荷节点集合；γi表示负荷等级因子，γi∈{1 ,2,3,5}，分别表示三级、二级、一级和特级负荷；pj,i表示在第j个元件故障时负荷i成功转供的概率，pj,i∈[0,1]。

2）系统停电风险指数ENSRI

考虑重要程度不同的负荷节点、负荷等级因子γi，系统停电风险指数ENSRI可定义为：

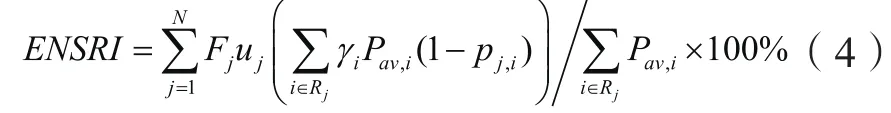
式中：uj为系统中元件j的平均停电持续时间(h/年)；Rj为元件j故障后影响的负荷节点位置集合；Fj为元件j的不可靠度，Fj= 1−e−λj Pav,i为负荷节点i的平均负荷值(kW).

1.2.1.3 经济性指标

1）配电企业投资VGC

配电企业投资包括投资成本与系统运行费用。投资成本包括线路扩容、主动控制系统、电力电子与通信系统三部分；而系统运行费用则包含系统设备维护、网损、DG、EES及电网购电的相关成本。

2）DG、EES、DSM投资成本VDG/EES/DSM

计及DG、EES以及DSM的投资成本：

式中：V1为DG投资年费用，V2为DG年运行费用。类似地，可得VEES/DSM的计算公式。

3）配电企业的年平均经济收益WGC

配电企业的经济收益主要来自延缓投资和售电收益：

式中：Wsd，Wyh，Wins分别为配电企业的平均售电收益，延缓投资收益以及规划前配电企业的原始收益（万元）；cav，，分别为平均售电电价（元/kWh）以及单位容量DG/EES对应的年等效缓建价（元）；,分别为节 点i上DG机组的额定装机容量（MW）及EES装置的额定蓄电量（kVAh）；RDG,REES表示系统中DG节点/EES节点位置集合；M为配电企业的总售电量（MWh），其计算公式如下：

式中：T为所研究时段持续时间（h）；为时段t内负荷节点i处DG/EES/DR及外部电网向系统的注入（充放电）功率（MW）；为馈线的网络损失功率（MW）。

4）DG投资商的经济收益W：DG投资商的经济收益来自售电收益：DG

式中：Tmax为DG的年利用最大小时数；cDG为DG对应的上网标杆电价（元/kWh）；cbt为新能源并网补贴电价（元/kWh）。类似地，可得到EES投资商经济收益WEES与需求侧集成投资商经济收益WDR。其中求解WDR中的cDR应为配电企业向需求侧集成服务商购买可中断服务的价格（元/kWh）。

5）DG运行效率ηDG

式中：PΣDG表示其余电源注入配网的有功功率；同理，可得到EES的运行效率指标表达式。

6）系统对DG的综合利用能力ξDG

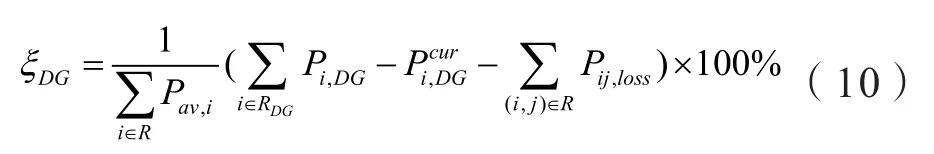
式中：为最优潮流下节点i处DG机组的功率削减值（MW）；Pi,DG为负荷节点i处的DG出力（MW）；Pij,lossPij,loss为线路ij上的功率损耗（MW）。

1.2.2 技术发展性指标

1.2.2.1 环境类指标

1）分布式电源渗透率：选取能量渗透率作为分布式电源渗透率的评价指标，定义为分布式电源全年提供的电量占系统负荷全年耗电总量的百分比。

2）低碳收益指标WC：有源配电网低碳收益主要考虑有能源终端收益与电能配送收益：

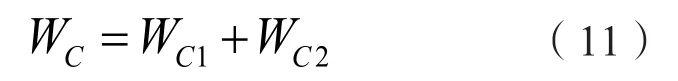
其中，WC1/WC2分别为终端能源环节/电能配送环节的低碳收益，定义为：

式中：εc,coal为主网的碳排放系数（kg/gce）；ccoal为主网单位电量对应的煤耗（gce/kWh）；ηloss为系统网损的预期降低率。

1.2.2.2 用户类指标

用户类指标包括阶梯电价实行用户比例及需求响应参与用户比例指标，反映电网与用户之间的信息互动能力及用户电价响应能力水平，可根据规划方案基本数据得到。

2 单主体有源配电网规划评估

基于有源配电网规划方案评价指标体系，采用带有AHP约束锥的SE-DEA交叉效率评估方法对各个待选规划方案的投资利用率进行分析，从而获得单主体下有源配电网规划方案的优劣排序和方案偏好。

2.1 AHP约束锥构建

层次分析法采用相对标度将决策主体的判断标量化，通过求解判断矩阵得出各指标的权重[16-17]。本文根据层次分析法构建AHP约束锥[18]的流程如下：

1）输入及输出指标规范化：以图1有源配电网规划方案评估指标集为研究对象，将隶属于主体k的成本型指标作为输入指标，收益型指标作为输出指标，得到m个输入指标xki(1 ≤i≤m)及s个输出指标ykj(1 ≤j≤s)。采用式（14）对输入及输出指标值进行规范化处理：

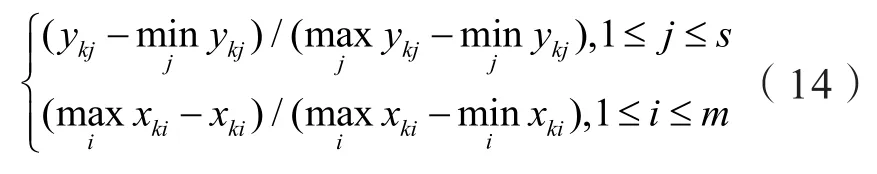
2）求解输入及输出指标的9标度判断矩阵：各决策主体根据9级标度法分别对xki及ykj之间的重要性程度进行打分，构建输入输出9标度判断矩阵按AHP方法对矩阵进行一致性校验，一般取一致性比率C.R＜0.1认为判断矩阵的一致性可以接受。

3）求取输入及输出指标权重：根据指标体系的层次关系，自上而下求解每层指标相对于总目标的权重，得到具有输入及输出指标权重向量及

4）构建AHP多面闭凸锥：设分别为输入输出判断矩阵的最大特征值，令构造指标的AHP偏好约束锥矩阵以及AHP多面闭凸锥：

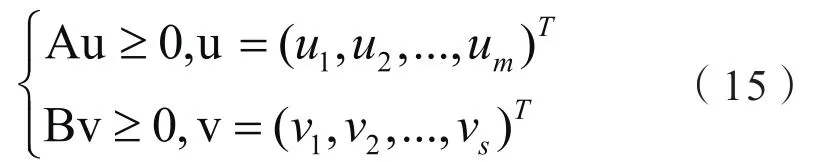
2.2 SE-DEA交叉效率评估方法

数据包络分析法是研究同类型生产决策单元(Decision Making Unit，DMU)相对有效性的有力工具[19-20]。对于n种有源配电网待选规划方案，定义方案k的效率评价指数ekk为其总输出与总输入比值：

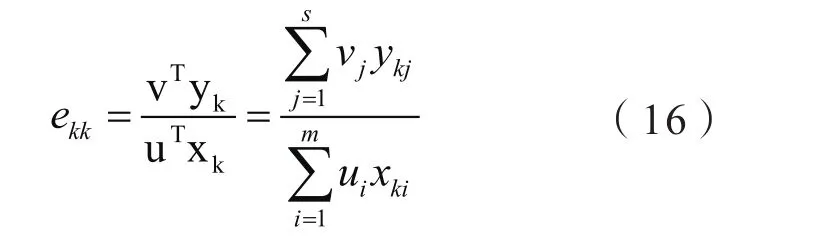
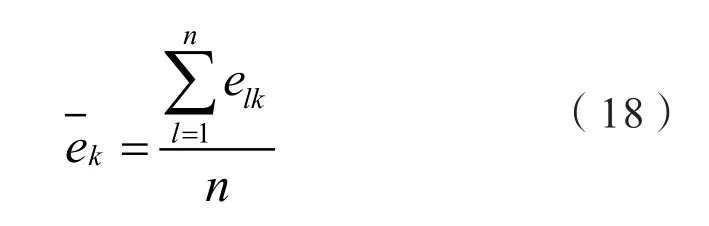
根据交叉效率值的大小即可对有源配电网规划方案进行决策排序，取交叉效率值最大的规划方案为最优方案。

当决策单元数目相对于输入与输出指标总数目较少时经常会出现若干单元的的情形，无法判断方案优劣。因此，采用超效率DEA模型（SE-DEA）对交叉效率矩阵的对角元素进行改进：

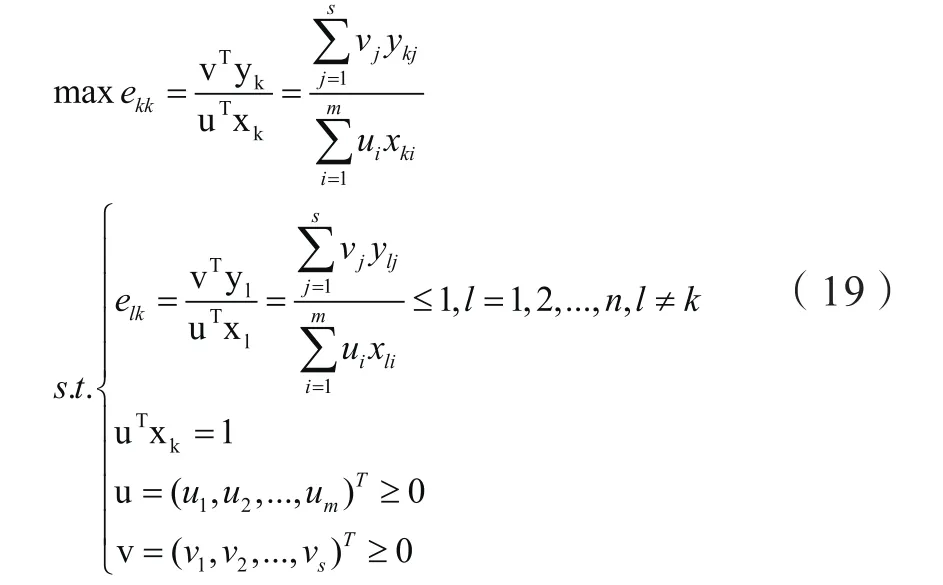
2.3 AHP约束锥SE-DEA交叉效率评估

将AHP约束锥纳入SE-DEA交叉效率评估模型中：

求解上式即可得出各规划方案的输入及输出指标向量以及超效率值。带有AHP约束锥的SE-DEA交叉效率评估模型构建流程如图3所示。

图3 带有AHP约束锥的SE-DEA交叉效率评估模型构建流程图

3 多元主体有源配电网规划协同评估

在电力市场环境下，为实现有源配电网规划投资群体利益最优，需构建信息交互、权重调整的协同评估机制，从而使具有不同偏好的利益主体做出一致性较高的方案选择。

3.1 多元主体协同评估问题描述

假设有源配电网规划建设有k个投资决策主体参与，协同评估的专家群体为K{dm,m=1,...,k}，备选的规划方案集为P{bn,n=1,...,p}。为第t轮决策者m的专家权重，∈ (0,1)且有根据第t轮的专家权重及其对规划方案的偏好信息，集结得到群决策的方案权重，通过对专家权重λm的自适应调整获得最终方案权重向量R=[r1,r2,...rp]T，选择最优的有源配电网规划方案作为决策结果。

3.2 多元主体协同评估流程

1）多元主体偏好信息一致化：假设有源配电网规划方案的主体m提供p个规划方案的偏好信息：满足将偏好信息化为互反判断矩阵Hm=[hij]p×p，hij=ei/ej。

2）群体偏好信息集结和基于灰色关联度的满意度函数：对各专家的偏好信息矩阵进行一致化处理后，得到k个对于规划方案集P的互反判断矩阵[A1,A2,...,Ak]，其中将其最大特征值对应的特征向量归一化可求出主体m对p个方案的权重向量则群体偏好通过WAA集结算子[21]得出

式中，a*ij表示群体认为方案bi优于bj的程度。同理可得有源配电网方案集中各方案的权重向量

以群偏好为参考序列，个体偏好为比较序列，衡量各规划评估专家对于结果的满意度及群偏好与个体偏好的一致度，构建基于灰色关联度的满意度函数：

a根据专家个体偏好矩阵Am与群体偏好矩阵 A*，计算关联系数矩阵

式中，η∈[0,1]为分辨系数。

b对于有源配电网规划决策主体dm，计算个体偏好于群体偏好的灰色关联度：

c构建基于灰色关联度的专家个体满意度函数，如图4所示。

图4 满意度函数

因此基于灰色关联度的个体满意度函数Ym(lm)可表示为：

d基于满意度和一致性的专家权重优化

为了在专家个体权重可变范围内获取一致性和满意度最优的规划方案，构建如下优化模型：

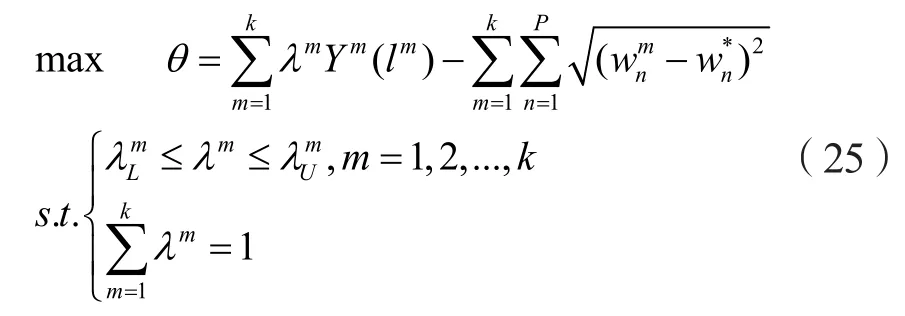
式中：目标函数θ的第一项最大化个体专家对群决策方案的满意度，第二项最小化专家意见偏好与群决策偏好的距离，λ0为专家初始权重。

4 算例分析

以我国北方某实际待建区域为例，结合本文建立的评价指标体系对有源配电网相关规划方案进行综合评估。

4.1 算例参数

待规划电网电压等级为10kV，预计规划年最大负荷20MW，年用电量1.27×105MWh，电网已有1座110/10kV变电站，92条规划可选线路以及22个负荷节点，如图5(a)所示。该地区初步拟定的3个有源配电网规划建设方案如图5(b)(c)(d)所示。

图5 待规划的区域及待选规划方案

4.2 评价指标计算

根据2.2节各项指标计算方法，得到各规划方案的评价指标结果。

4.3 规划方案综合评估

4.3.1 单主体下规划方案评估

4.3.1.1 配电企业

方案3的系统整体安全系数指标偏离约束区间，不满足配电企业的规划要求，因此将方案3从待选方案集中剔除。对弹性指标进行带有AHP约束锥的SE-DEA交叉效率评估如下：

1）将隶属于配电企业的弹性评估指标集分为C41输入及C32/C43/C52输出指标，并根据式（14）进行规范化处理；

2）收集专家偏好信息，采用AHP法得到各指标主观权重向量w =[0.1522,0.6847,0.1631]T；

3）构造输出指标的AHP约束锥矩阵：

4）计算得到各规划方案的交叉效率值

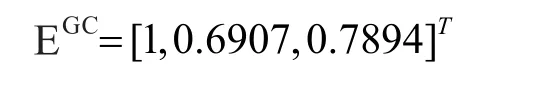
根据结果可知，面向配电企业的方案排序为方案1＞方案3＞方案2，方案1与3较方案2具有更优的投入产出水平，但由于方案3有刚性指标偏离约束区间，因此修正后排序为方案1＞方案2（方案3剔除）。

4.3.1.2 DG/EES投资商与DSM集成商

由于对应刚性指标校核均满足约束，因此对弹性指标进一步评估：

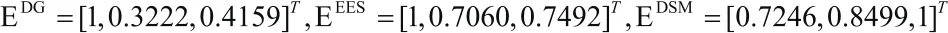
各主体对应的弹性评价指标均为单投入单产出指标，因此可按各主体总投资成本与总经济收益的比值得到不同方案下的投资利用率：根据结果可知，面向DG/EES投资商时的最优方案为方案1，面向DSM集成商时的最优方案为方案3。综合面向配电企业的方案评估结果，可知在考虑多元主体的差异性需求时，规划方案的排序结论可能不一致，因此难以应用一个简单的排序结果来兼顾不同利益主体的需求。

4.3.2 多元主体下规划方案协同评估

2）收集各主体专家的偏好信息，形成4种主体下对3种方案的互反判断矩阵Hm：

3）得到初始群体偏好信息矩阵A*,0，归一化后得到初始方案权重向量w0：

4）取分辨系数η=0.9，根据各主体偏好矩阵Am与群体偏好矩阵A*,0，计算关联系数初始矩阵Fm和各主体与群体的灰色关联度初始矩阵L0：

5）设置满意度函数及满意值区间[0.85,0.93,1.0]，对专家个体权重进行优化计算，得到一致性和满意度最优的群体偏好矩阵A*、各主体满意度向量Y及各方案的最终权向量W：

由W可知，采用有源配电网规划方案多主体协同评估方法得到的方案排序为方案1＞方案2＞方案3，配电企业及EES投资商对于排序的满意度较高，而DG投资商及需求侧集成商对于排序的满意度较低，但仍可接受，因此选取方案1作为兼顾多主体利益需求的有源配电网最优规划方案。

由结果可知，在本文的专家权重设置前提下，由于配电企业的专家初始权重较高（0.557），使其在协同评估过程中起主导作用，在其他主体的满意度允许区间内，群偏好向配电企业的偏好靠拢。

5 结束语

本文建立了有源配电网规划方案的评价指标体系，并分别从单主体与多元利益主体的角度提出了综合主客观因素的评估方法，算例表明面向多元主体的协同评估可以获得兼顾各个主体利益的规划方案。主要得出结论如下：

1）文中所提评价指标体系计及了有源配电网的主要技术特征，并对规划过程涉及的各利益主体进行了指标划分，可从不同主体的角度对规划方案的性能进行全面有效的评价。

2）当某主体的专家初始权重设置较高时，其在协同评估中将会起主导作用。然而，随着未来分布式可再生能源和储能等技术的发展，各利益主体的专家权重和满意度区间将会发生变化，最终的评估结果亦会随之改变。

由于配电网规划过程中涉及的不同主体初始专家权重构成复杂，后续应考虑投资成本、运营角色以及国家政策等因素的影响，对初始专家权重进行进一步的研究分析。此外，由于有源配电网中的需求侧响应机制复杂，如何在评估指标及计算方法中有效计及不同类型的柔性负荷和不同激发机制的需求侧响应亦值得未来进一步讨论。