计及负荷匹配度扶贫地区光伏电站多目标规划

刘宝林，王芳，李小双

（1.云南电网有限责任公司电网规划建设研究中心，昆明 650011；2.天津楚能电力技术有限公司，天津 300384）

0 前言

村级光伏扶贫电站一般安装于配电线路的末端，电网网架结构较为薄弱，电网供电能力不足，存在断电、限电问题。扶贫光伏的接入在一定程度上改善线路末端的供电能力，缓解了电网末端单一电源的问题[1]。

然而，由于扶贫光伏电站接入点多且较为分散、技术规范性差，分布式光伏的随机性、波动性较强，大量扶贫光伏接入也增加了电力系统运行的风险，光伏出力的不确定性极易导致配电网电压越限，是影响光伏接入配电网的主要问题之一。文献[2]对分布式光伏发电对配电网电压的影响进行了分析，研究了光伏大小、接入位置和负荷大小等影响电压变化的因素，提出了电压越限的解决方案。文献[3]针对高渗透率下的光伏接入，考虑到光伏出力与负荷的不平衡问题，采用利用光伏系统逆变器的控制措施缓解并网节点的电压越限。文献[4]提出了一种考虑静态电压稳定约束的DG规划模型，模型考虑了DG接入对于静态电压稳定裕度的影响。文献[5]提出了一种考虑电压稳定裕度的配电网光伏规划方法，规划模型基于多场景考虑了光伏出力和负荷的匹配程度。

以上文献的分析表明，光伏接入对于配电网运行的影响和区域负荷特性密切相关，当光伏出力和负荷特性匹配程度较高时，可以实现良好的就地消纳效果，不易产生电压越限；反之则会危及配电网运行。

同时，光伏电站规划过程中应充分考虑电站建设经济性的影响，科学配置扶贫光伏并网带来的配电网配套投资，减少无效投资或冗余投资。在贫困区县和国家扶贫开发工作重点地区，利用村集体未利用土地建设小型分布式光伏电站，确保贫困户每年获得稳定的收入。光伏电站建成后的良好收益将有助于提升投资方的后续建设积极性，从而有效推进精准光伏扶贫项目。文献[6]在保障分布式发电商利益的前提下，以配电公司收益最大化为目标，考虑系统安全约束，构建了分布式发电接入后有源配电网的综合投资规划模型。文献[7]所构建模型的目标函数是配电网建设成本与运行费用最小化，采用改进的免疫克隆算法作为求解方法。文献[8]建立了分布式电源社会福利最大化和利润最大化两目标模型，采用多目标算法进行了求解。文献[9]考虑光伏接入对于延缓配电网改造的作用，建立了包括延缓网络改造收益、缺电成本和购电成本等。

因此，在当前国家对于光伏发电建设规模和项目管控愈加严格的背景下[10]，本文综合考虑光伏出力和负荷匹配程度以及光伏电站建设收益，提出了一种适用于扶贫地区光伏电站多目标规划方法。从配电网运营者(Disco)的角度出发，将光伏出力和负荷的匹配度作为一个规划目标，以限制光伏接入对于配电网安全运行的影响；从分布式电源投资商(DGO)的角度出发，将光伏电站扶贫综合效果作为另一个规划目标，体现扶贫地区光伏电站建设的经济性，从而保证扶贫地区规划方案总体最优。

本文首先基于序列运算理论建立了光伏出力和负荷序列模型；其次，提出光伏出力和负荷匹配度的评估方法，以配电网安全运行作为约束条件；再次，提出了光伏电站扶贫综合效果计算方法。在此基础上，利用NSGA-II和TOPSIS算法归纳了多目标模型的求解流程；最后，在典型场景下验证了规划方法的有效性。

1 序列运算的光伏和负荷概率模型

目前，对于光伏出力的建模方法有基于历史光强概率分布抽样的时序模型、光伏出力Beta分布抽样和半不变量法等。考虑到时序抽样方法计算量较大，而半不变量方法准确性较差，本文采用序列运算理论建立光伏出力和负荷概率模型，其具有计算速度快，概率分布精确等优点[11]。

序列是指定义在数轴上非负整数点上的一系列数值，将其表示为a(i)，且i=0,1,...,Na，对于所有i＞Na，a(i)=0。而i=Na，且a(Na)≠0 时，Na即为序列a(i)的长度。为了描述某些随机变量的概率分布特性，并通过序列间的运算来对一个或多个随机随机变量进行处理，定义了概率性序列及其运算，以求解多个随机变量之间的联合分布[12]。

概率性序列的定义为：对于长度为Na的序列a(i)，若0≤a(i)≤1(i=0,1,...,Na)，且a(i)(i=0,1,...,Na)之和为1，则a(i)为一个概率性序列。

1.1 光伏出力的序列化模型

对于满足两参数Beta分布光照强度，其概率密度表达式为：

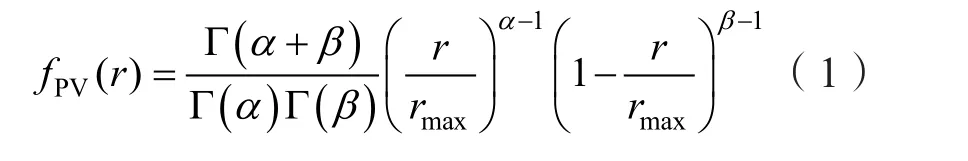
式中：r和rmax分别表示仿真周期内的实际光强和最大光强；Γ为Gamma函数；α和β为Beta分布的形状参数，可由不同场景下的光照均值和方差得到。式（1）对应的累计分布函数为：

假定光伏出力和光强满足以下线性功率关系：

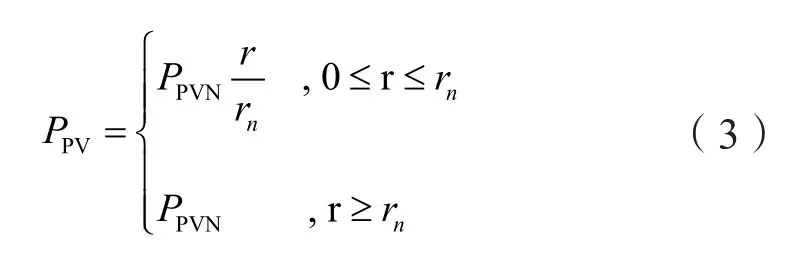
式中：PPVN为光伏阵列的额定功率，rn为额定光强。将序列的离散化步长设置为ΔP，则光伏出力的概率性序列为：

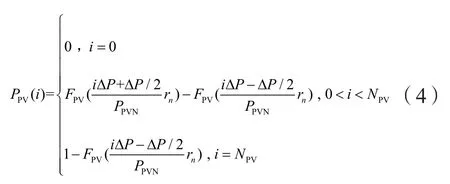
式中：NPV为光伏出力序列长度，NPV=PPVN/ΔP。通过式（1）至（4），即将光伏出力离散为概率性序列。

1.2 负荷序列化模型

负荷的概率特征可以采用正态分布进行描述，表示为PL～N(μ, σ2)，其中μ为负荷期望值，σ为方差，对其概率密度函数进行积分，可得到其累计概率分布函数为：

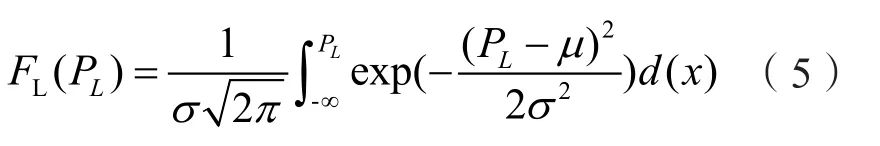
将负荷序列离散化步长设置为ΔPL，则负荷的概率性序列如式（6）所示：

式中：NL为负荷序列长度，NL=PL/ΔPL。

2 光伏出力和负荷匹配度评估模型

光伏出力和负荷的匹配程度将对区域配电网的运行产生较大影响，因此，在光伏电站选址定容过程中，需要考虑光伏电站和当地负荷匹配程度的影响。本文把相关矩阵法[13]和序列运算理论结合，建立反映光伏出力和负荷匹配程度的评估模型。

假定所评估的系统中共有m个相关的随机变量p1,p2,...,pm，将其记为向量P=(p1,p2,...,pm)。向量P中的a个元素变量表示光伏电站的出力，其均服从Beta分布，分别为p1,p2,...,pa；有m-a个元素变量表示负荷大小，其满足正态分布，分别为pa+1,pa+2,...,pm。变量pi和pj的相关系数为ρij，f(pi)和F(pi)分别为变量pi的概率密度函数和累计概率密度分布函数（i,j=1,2,...,m）。

根据等概率转换原则[14]，将向量P转化为标准正态随机向量Y=(y1,y2,...,ym),相应的元素变量yi和yj之间的相关系数为ρyij。

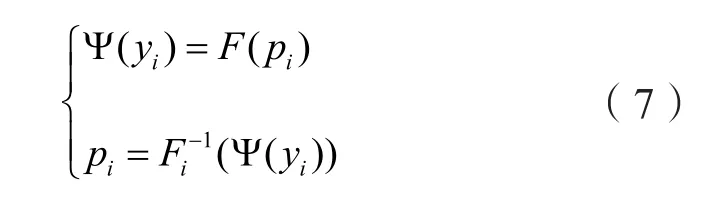
式中：ψ(yi)为yi的标准正态分布累计分布函数；F-1

i为累计分布函数的反函数。根据相关系数的定义，可得到转换前后的随机变量之间的函数关系为：

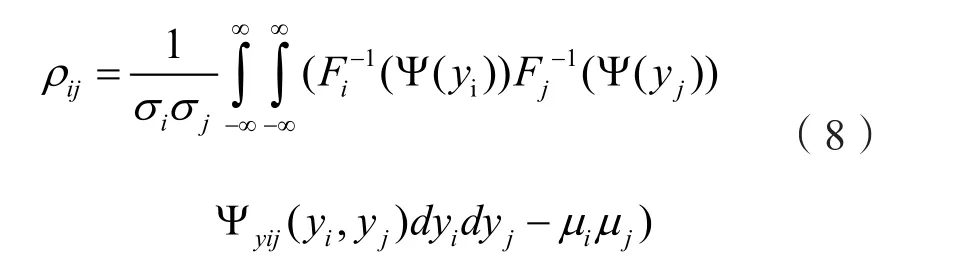
式中：ψyij表示标准二元正态分布的概率密度函数，其相关系数为ρyij。

Y的协方差矩阵Cy为：

基于Cholesky分解将Y转换为互相独立的标准正态分布随机向量，将其按照式（10）所示进行分解：

式中：BT为分解得到的下三角矩阵，由式（11）即可实现向量Y到标准正态随机向量H的分解。

结合序列运算理论，对标准正态随机向量H进行处理。在序列运算中，对于长度分别为Na和Nb的概率性序列，两序列的卷和运算定义为：

式中：x(i)为联合概率分布序列，其序列长度Nx=Na+Nb；i=0,1,...,Nx。则对于相关性矩阵H，结合序列运算理论将其各元素进行归一化处理。

假定准备规划的光伏电站总数为a，该区域负荷总数为b，则第l个光伏电站(l=1,2,...,a)的出力序列和第k个负荷点(k=1,2,...,b)之间的匹配度可以归一化处理表示为：

式中：H(l,k)为归一化矩阵中第l行第k列的元素。

对于共有a个光伏电站的一组规划方案，将其总负荷匹配度最大作为一个规划目标：

同时，为保证光伏电站接入后不会越严重危及配电网运行，设置以下约束条件：

2.1 节点潮流约束

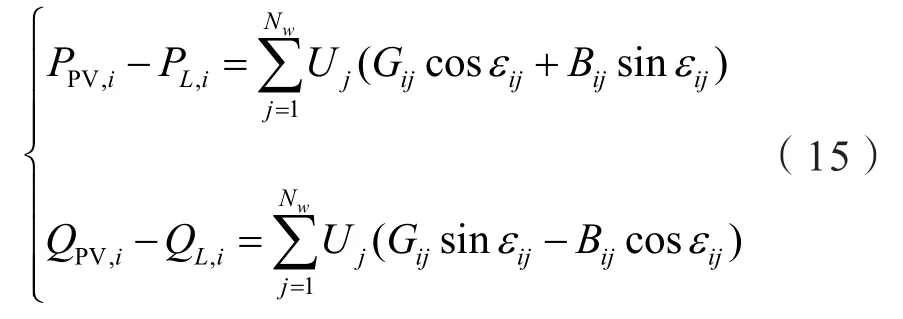
式中：PPV,i和QPV,i分别为节点i处光伏的有功和无功出力；PL,i和QL,i分别为节点i处有功和无功负荷；Ui为节点电压大小；Gij和Bij为线路导纳；ε为节点电压相角差；i和j均为配网中某节点。

2.2 节点电压运行约束

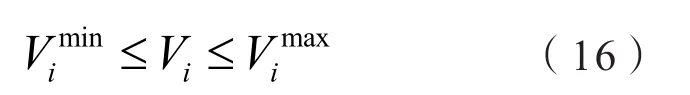
式中：和为配网节点i电压的上下限。

2.3 支路双向潮流约束

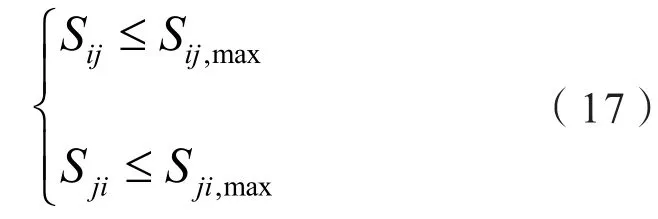
式中：Sij和Sji分别为支路ij正向和反向传输功率；Sij,max和Sji,max分别为支路ij正向和反向传输极限功率。

2.4 分布式电源安装位置约束

式中：NPV为实际接入的光伏电站数目；NPV,max为由于政策或管理原因所允许接入的光伏电站数目上限。

3 光伏电站扶贫综合效果计算

光伏电站的运行收益直接影响着投资商后续建设的积极性，良好的投资收益可以有效提升投资商的后续建设意愿，从而推动光伏发电在全社会范围内的推广。因此，本文主要从配电网投资商(DGO)的角度出发，以下计算其综合收益。

在光伏电站运行期间，综合考虑其各类型收益，将综合收益最大作为一个目标函数：

式中：Noper为光伏电站运行年限；Sele为电站运行年限内的总售电收益；Srel为由于光伏电站接入所导致的配电网可靠性改善所获得的收益；Ccon为光伏电站建设成本；Coper为电站运行成本。

3.1 总售电收益

光伏电站通过向用户售电获取收益，该部分收益Sele收益计算如下：

式中：Ny表示光伏电站在第y年的有效运行小时数；NPV表示光伏电站数目；Δt为单位时间仿真步长；PPV,y,t,d表示第y年的第t个时段的第d个电站的功率；pele为单位电量价格；λy为第y年的折现率，其计算方法如下：

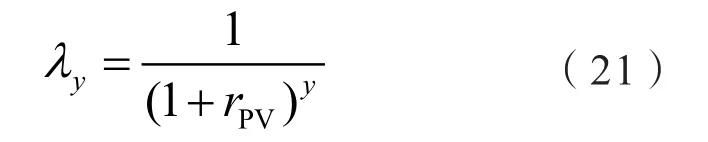
3.2 改善扶贫区域配电网可靠性收益

在配网发生故障时，光伏电站可通过孤岛运行为区域负荷供电，提高了供电可靠性。此时，认为电站可通过配电网公司或用户获得额外收益，该部分收益Srel计算如下：

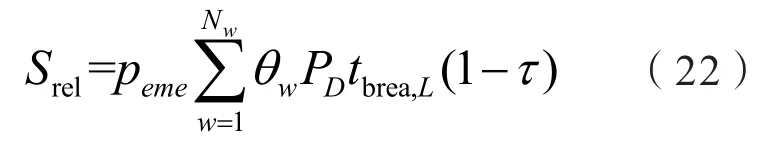
式中：peme为紧急供电情形下单位电量的额外价格；NL为负荷点数目；θL为第w个负荷点的年平均停电频率和平均停电市场；PD为光伏电站孤岛运行期间负荷的平均需求功率；tbrea,L为第L个负荷点的平均停电持续时间；τ为停电期间形成孤岛供电失败的概率。

3.3 光伏电站建设成本

光伏电站投建成本如式（23）：

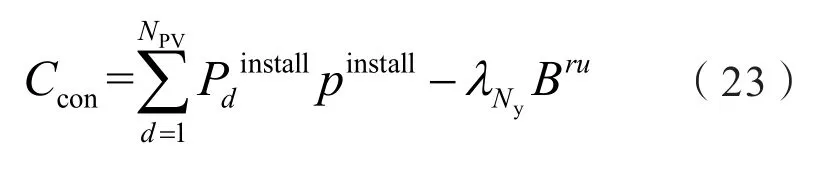
式中：为第d个光伏电站的装机容量；pinstall为单位光伏容量的装机成本；Bru为光伏电站设备回收残值，其只在电站运行的最后一年计入收益。

3.4 运行维护费用

电站运行期限内的运行维护费用计算如下：

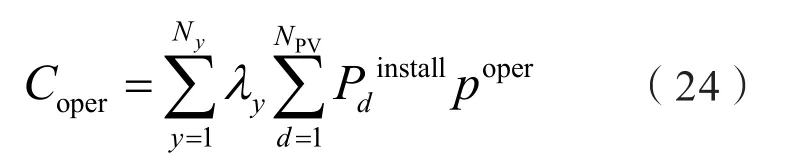
式中：poper为单位光伏机组容量的运行维护成本。

4 基于NSGA-II的多目标求解方法

在多目标协同优化问题中，多个目标函数很难同时达到最优，目前典型的多目标求解方法有DEA方法、加权系数法和Pareto前沿[15]等。其中，Pareto前沿可以直观的展现各个规划方案之间的优劣关系，从而有助于做出最优决策。本文采用NSGA-II算法求解Pareto前沿，结合TOPSIS排序方法对Pareto前沿进行排序，以期得到最优规划方案。

4.1 NSGA-II算法

NSGA-II即为带精英策略的非支配排序的遗传算法，其通过快速非支配排序降低了计算复杂度；同时采用精英保留策略避免了父代中优良个体丢失；其引入了拥挤度和拥挤度比较算子，保证了种群多样性，保证解可以扩展到整个帕累托域。具体求解流程如下：

图1 NSGA-II方法求解流程

4.2 TOPSIS排序方法

利用NSGA-II多目标算法完成多目标求解得到Pareto前沿后，采用TOPSIS排序方法对Pareto前沿进行排序，选取最优规划方案。

TOPSIS排序法的基本原理是从Pareto前沿中寻找各项指标函数的最优值，将其定义为“理论最优解”，同理定义“理论最劣解”。检测评价对象与“理论最优解”和“理论最劣解”的距离来进行排序。当某评价对象既最靠近最优解又最远离最劣解，则认为该方案是最优规划方案。

TOPSIS排序算法的计算流程如下[17]：

1）原始数据归一化处理：

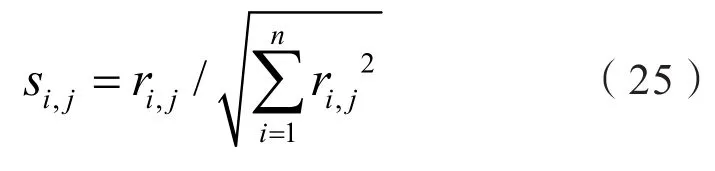
式中：ri,j、si,j为第i组规划方案的第j个目标函数在归一化前后的值，n为Pareto前沿中解的个数，此处即为将负荷匹配度目标和扶贫综合效果目标进行归一化；

2）寻找各项目标函数归一化后的最优值和最劣值，得到“理论最优解”(q1,q2,...,qn)，其中qi为所有si,j中的最优目标函数(i=0,1,...,n)。同理得到和“理论最劣解”(e1,e2,...,en)为对应的最劣目标函数值；

3）计算所有解与“理论最优解”和“理论最劣解”之间的距离：

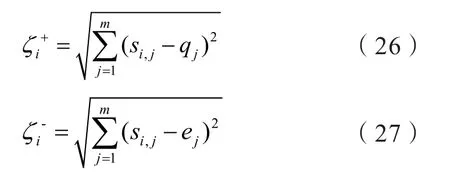
4）按照式（27）计算所有规划方案的理想度，对其排序得到最优解：

5 算例分析

5.1 场景设置

以IEEE 33节点作为算例场景进行测试，节点电压标幺值范围为0.95-1.05，为体现光伏出力和不同特性负荷的匹配度，将20-23和31-33设置为工业负荷，节点7-10和15-18为商业负荷，其余为居民负荷，各类负荷曲线详见文献[18]。

负荷年增长率设置为3%，规划年限为15年，电站残值率为10%，贴现率为5%，光伏平均投资成本为4元/W，运维成本为0.25元/W，上网电价为0.43元/kw·h,政府补贴电价为0.42元/kw·h。支路正向潮流上限为10kVA，反向潮流上限为4kVA，各负荷点的可靠性参数参考文献[19]。

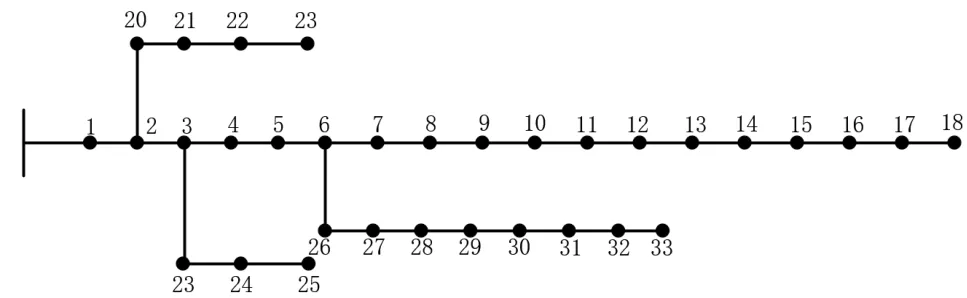
图2 IEEE 33节点测试线路

所建设光伏电站数目最大为4座，NSGA-II算法种群数目为150个，最大进化代数为100代，交叉概率为0.8，变异概率为0.2。

5.2 固定渗透率下规划结果

定义渗透率是指光伏出力与装机容量的比值，将光伏出力渗透率为0.8，通过4.1节算法流程进行求解得到Pareto前沿，结果如图3所示。

分析该图可知，当所规划光伏电站的出力和负荷匹配度较高时，其对于配电网安全运行的影响相对较小，可保证配电网安全运行，最大总体匹配度约为0.65，此时DGO的综合年收益约为400万元；当DGO综合年收益较大时，光伏电站和负荷匹配度较低，电站对于配网安全运行可能产生较大隐患，最大综合年收益约为2500万元，此时的总体匹配度约为0.04。因此，负荷匹配度和扶贫综合效果难以同时达到最优，需要在两个规划目标之间寻找平衡。

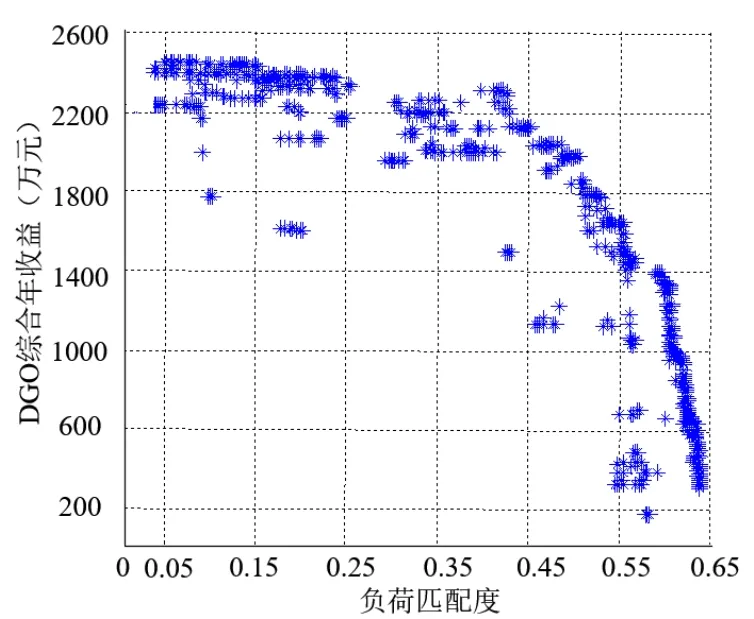
图3 Pareto前沿求解结果

通过4.2节的TOSIS排序方法，对帕累托前沿进行排序，将理想度排名前3的规划方案展示如表1。

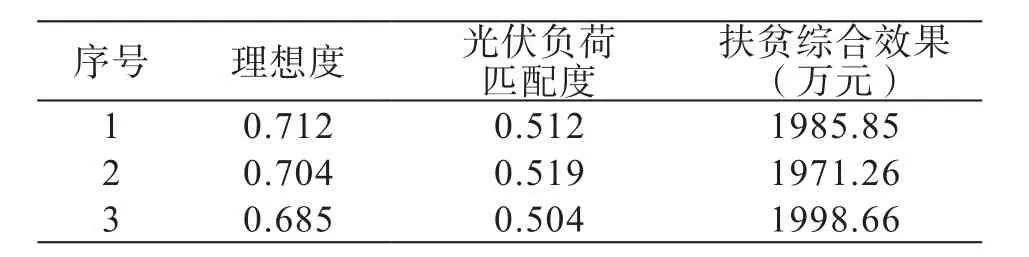
表1 理想度较高的规划方案

表1中，方案2的光伏负荷匹配度最高，但是规划收益较低；方案3的综合年收益最高，但是光伏负荷匹配度相对较低；方案1的两个规划目标均居中，但是经算法排序，该方案为相对最优规划方案，其理想度为0.712，具体投资建设方案可结合当地对于经济发展和配网运行的实际需求进行选取，方案1的具体规划结果如表2所示。

表2 最优方案规划结果

对最优规划方案进行分析：从负荷特性来看，光伏电站建设的负荷节点主要为工业和商业负荷，主要是由于工业和商业负荷白天负荷较重，和光伏出力特性相对较为一致，而居民负荷主要集中在夜间和光伏出力匹配度较差；从接入位置来看，主要集中在线路末端，是由于线路末端建设光伏电站对节点电压具有良好的抬升效果，减少了电压越限的可能性。

5.3 不同渗透率下结果分析

5.2 节对固定光伏渗透率下的规划结果进行了分析，考虑到光伏出力的不确定性，对不同出力渗透率下的最优规划结果进行对比，结果如表3所示。

表3 不同渗透率下的规划方案对比

分析不同渗透率下的最优规划方案可知，对于光伏渗透率的设置会影响光伏电站规划结果：光伏渗透率较高时，对于光伏出力的预计偏向于保守，最优规划方案的光伏和负荷匹配度较高，DGO综合年收益逐渐下降；反之，当光伏出力渗透率较低时，所评估的负荷匹配度较低，但是DGO预计年收益较大。因此，实际规划方案需要在配网安全运行和经济收益之间寻找平衡。

6 结束语

由于大量扶贫光伏接入，光伏出力不确定性极易导致配电网电压越限。基于扶贫光伏接入对于配电网运行的影响和区域负荷特性密切相关，本文提出了一种计及负荷匹配度的光伏扶贫村级电站多目标规划方法，主要工作如下：首先，基于序列运算理论建立了光伏出力和负荷模型；其次，将相关矩阵法和序列运算理论结合，提出了光伏出力和负荷匹配度计算方法；再次，建立了光伏扶贫电站的综合收益计算模型；最后，基于NSGA-II和TOPSIS算法对多目标规划模型进行了求解，验证了规划方法的有效性。分析结果表明，光伏扶贫电站的规划方案需要在负荷匹配度和经济收益之间寻找平衡，同时，不同地区的光伏出力渗透率会对规划结果产生较大影响。