具有不对称非线性项平面系统周期解的存在性∗(上)

马 田 田

(首都师范大学,北京 100048)

1 前言及主要结论

考虑平面系统

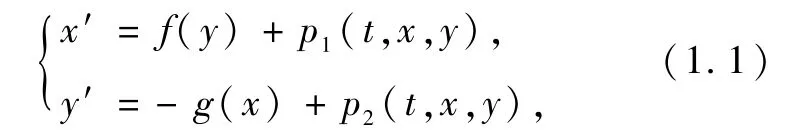
其中f,g∶R→R连续,pi∶R3→R(i=1,2)连续且关于第一个变量t是2π周期的.

系统(1.1)可以写成如下形式

周期解的存在性.假定下面的非对称条件成立,

和

这里a±,a±,b±和b±都是正常数.若存在正整数n使得

和

文献[10]证明了系统(1.3)至少存在一个周期解.关于其它相关的结果可见[3,7,8,12-15].

本文在新的条件下研究系统(1.1)周期解的存在性.假定g满足条件

f在无穷远处满足非对称条件,

和

另外,假定存在常数M0＞0使得

(h4)对任意t,x,y∈R,有|pi(t,x,y)|≤M0,(i=1,2).

本文将借助于时间映射来研究系统(1.1)周期解的存在性.令

τ(c)通常称为时间映射.文献[5,6]深入研究了映射τ的性质.记

应用连续性定理[2],本文证明了以下结论：

定理1.1假定条件(hi)(i=1,…,4)成立.若存在一个正整数n使得不等式

定理1.2假定条件(hi)(i=1,…,4)成立.若不等式

成立,则系统(1.1)至少存在一个2π周期解.

若存在正常数a,b使得

可以得到如下结论：

推论1.3假定条件(hi)(i=1,4,5)成立.若存在正整数n使得不等式

至少存在一个2π周期解,这里y+=max{y,0},y-=max{-y,0}.

注记1.4推论1.3推广了[6]中的结果.文献[6]证明了若存在一个正整数n使得不等式

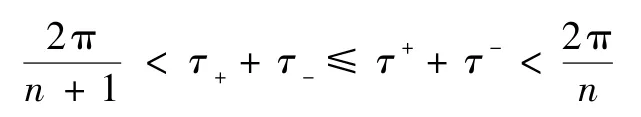
成立,则Duffing方程

至少存在一个2π周期解.因为方程(1.6)等价于系统x′=y,y′=-g(x)+p(t),故有f(y)=y.这样a=b=1,从而因此,条件(τ2)正好是[6]中的条件.

2 一个连续性定理

本文将应用[2]中的连续性定理证明系统(1.1)周期解的存在性.为方便起见,下面先介绍这一定理.

考虑系统

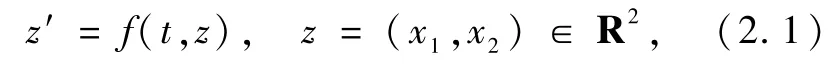
这里f∶R3→R2连续并且对任意(t,z)∈R3,f(t+T,z)=f(t,z).将系统(2.1)嵌入到含有单参数λ∈[0,1]的方程族

其中F∶R3×[0,1]→R2连续,并且对任意(t,z,λ)∈R3×[0,1],有

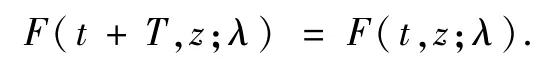
另外,F满足

定理2.1(连续性定理)[2]假定下列条件成立,

(1)存在正常数r0使得对于z′=f0(z)任意T周期解z(·),都有|z|∞≤r0,这里

(2)对任意r≥r0,dB(f0,B(0,r),0)≠0,其中

(3)对任意r1≥0,存在r2≥r1使得对于系统(2.2)的任意T周期解z(·)(λ∈[0,1]),

(4)对任意正整数n,存在rn＞0使得对于系统(2.2)的任意T周期解(λ∈[0,1]),n(z)=这里n(z)表示周期解z(·)的旋转数.则系统(2.1)至少存在一个T周期解.

3 基本引理

考虑含有单参数λ∈[0,1]的平面系统

令(x(t),y(t))=(x(t,x0,y0,λ),y(t,x0,y0,λ))表示系统(3.1)满足初始条件(x(0),y(0))=(x0,y0)的解.在本节中我们总是假定条件(hi)(i=1,…,4)成立,记

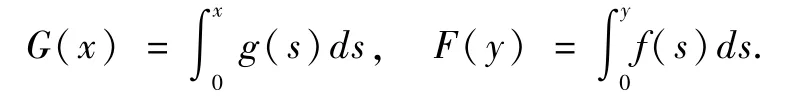
下面给出系统(3.1)柯西问题解的大范围存在性.由参考文献[16]可得如下引理.

引理 3.1[16]系统(3.1)的任意解(x(t),y(t))在整个t轴上有定义.

由文献[17]中定理6.5的证明可知下面的弹性性质成立.

引理 3.2对任意R1＞0,存在R2＞R1使得下面的结论成立,

引理 3.3[16]存在R0＞0使得当时,θ′(t)＜0,t∈[0,2π].

引理 3.4假设条件(τ0)成立.设{(xj(t),yj(t))}是系统(3.1)的一个2π周期解序列,其旋转数n(xj,yj)=k(k是一个固定的正整数),j=1,2,…,并且

引理 3.5假定引理3.4的条件成立.则有