填土地基强夯有效加固深度的数值模拟研究

罗玮

(长沙市规划勘测设计研究院，湖南 长沙 410007)

1 引 言

强夯法是一种最普遍的地基处理方法。强夯法因其具有施工快速、效果显著且设备简单的特点而被广泛运用在人工填土，砂土，粉土等地基土的加固处理，虽然强夯法发展较快，但仍然缺乏成熟的理论，施工过程中主要以经验为主，或通过试夯来确定施工参数。其中有限加固深度对于控制施工质量起着至关重要的作用，有效加固深度就是在强夯作用下地基土的强度得到显著提高并能满足工程需要的加固深度，通过总结前人的理论，主要存在以下计算方法：

(1)Menard经验公式：

(1)

式中：De为有效加固深度；M为夯锤质量；H为夯锤落距。

(2)后来学者们通过研究又对Menard经验公式进行了修正，称为Menard修正公式：

(2)

式中：α为修正系数。

(3)张利洁等[1]提出了如下计算公式：

(3)

式中：h为强夯有效加固深度；△h为夯沉量；e0和e分别为强夯前后孔隙比。

(4)左名麒[2]提出有效加固深度公式：

(4)

式中：rs为有效加固深度；k一般为3～5；W为夯锤质量；H为夯锤落距；vp为纵波波速；α为土体能量吸收系数。

由于强夯法所处理的地基土十分复杂，且不同施工参数也会产生影响，仅运用理论计算公式存在很大的局限性。而在数值模拟分析时，可以针对不同的地层以及施工方法输入其对应参数，使模拟更接近实际情况，其模拟结果也更为精确。

基于这一认识，本文运用数值模拟分析方法对填土地基的有效加固深度进行研究，并提出回归方程，对于强夯有效加固深度的估算具有一定的参考价值和指导意义。

2 强夯碰撞数值分析理论

2.1 土体本构模型

强夯作用下，地基土产生了弹塑性变形，因此本文采用的是弹塑性本构关系[3]：

{dσ}=[Dep]{dε}

(5)

式中：dσ为应力增量；dε为应变增量；[Dep]为弹塑性矩阵。

(6)

式中：[D]为弹性矩阵；f为屈服函数；g为塑性势函数；A为加工硬化模量。

2.2 土体动力平衡方程

为研究强夯动力响应，本文采用改进拉格朗日格式法，得到的土体动力平衡方程[4]为：

(7)

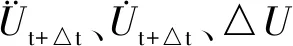
2.3 强夯冲击荷载模式

专家学者们通过实测整个夯击过程，得到的应力波只有一尖峰，未出现明显的第二波峰，作用时间仅为 0.04 s～ 0.2 s。吴铭炳[5]等将这种瞬态荷载简化成三角形。因此本文也将夯击能作用过程简化为三角形，如图1所示。

(9)

(10)

(11)

s=2rE(1-μ2)

(12)

式中：Pmax为锤底接触最大动应力(MPa)；v0为夯锤落地的速度(m/s)；m为夯锤质量(kg)；r为夯锤半径(m)；s为弹性常数；E为变形模量；μ为泊松比。

3 强夯碰撞建模

本文以强夯碰撞数值分析理论为基础，运用数值模拟软件ANSYS/LS-DYNA，通过建模并结合有限元法对强夯过程进行模拟。

本次模拟对象为泉塘(三期)安置小区填方区的强夯加固项目，为减少计算量和计算时间，在不影响结果的情况下，将夯锤和土体各取1/2按轴对称条件进行建模。

对于夯锤模型，其弹性模量为 2.04 GPa，密度为 7.80 t/m3；对于地基土模型选择弹塑性模型一双线性随动模型，其物理力学参数如表1所示。

地基土的参数 表1

图2 夯锤和土体模型

研究中选用的夯击能分别为100 T·m、150 T·m、200 T·m、250 T·m和300 T·m。为节省篇幅，本文仅选用150 T·m和300 T·m的模拟结果进行分析，其他夯击能分析原理和过程基本一致，不再赘述。

4 数值模拟结果及其分析

4.1 夯击能为150 T·m时数值模拟分析

图3为夯击能为150 T·m时的土体中各点竖向位移的等值云图。

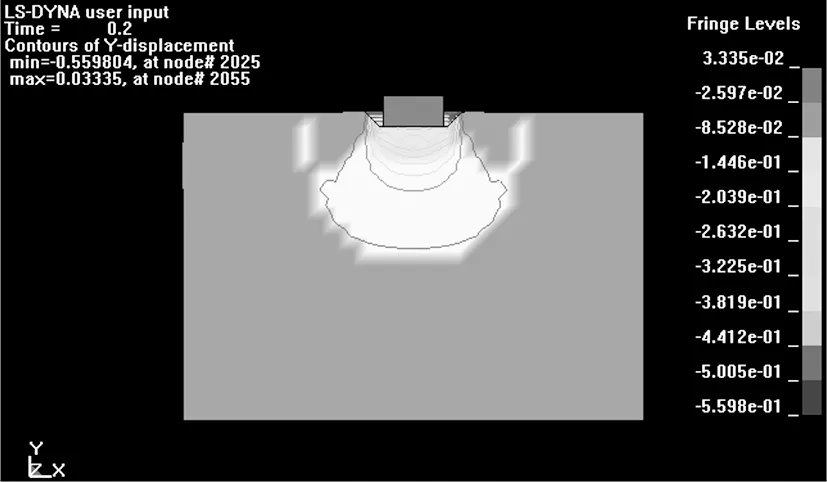
图3 土体竖向位移等值云图(150 T·m)

夯锤底部中心线以下不同深度处的竖向位移数据，如表2所示。

土体竖向位移数据汇总表(150 T·m) 表2

为更加直观，将表2中的数据绘制成变化曲线，如图4所示。

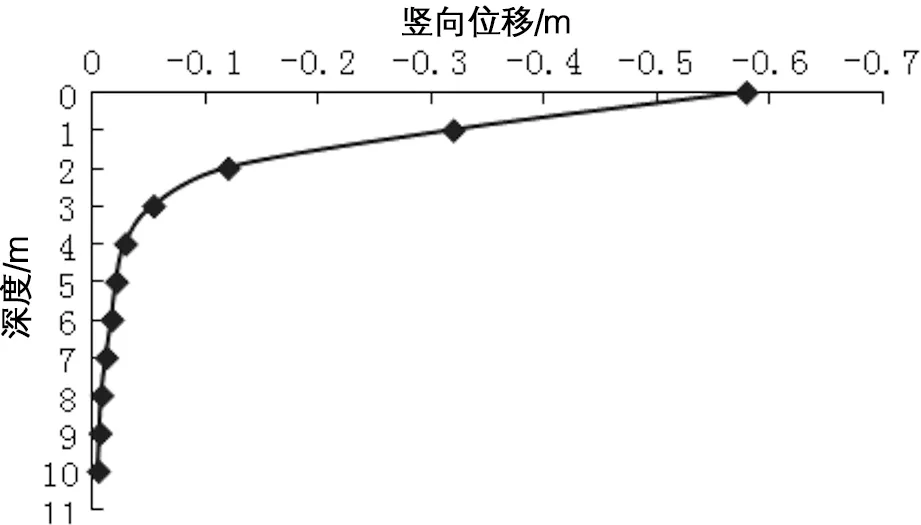
图4 土体竖向位移随深度变化曲线(150 T·m)

根据图4可知，随着深度的增加，土体竖向位移逐渐衰减。竖向位移在 4 m深度内衰减幅度较大，在 4 m以下深度衰减幅度急剧减小。

参考王铁宏[6]书中提到的有效加固深度判别标准：有效加固深度一般为土体竖向变形量为地表夯沉量5%的深度，下同。

通过分析表2中数据可知，以地表夯沉量 0.58 m的5%即 0.029 m的计算点深度为强夯有效加固深度的界限值，对表2使用内插法，可得到强夯有效加固深度约为 4.0 m。

4.2 夯击能为300 T·m时数值模拟分析

图3为夯击能为300 T·m时的土体中各点竖向位移的等值云图。

图5 土体竖向位移等值云图(300 T·m)

夯锤底部中心线以下不同深度处的竖向位移数据，如表3所示。

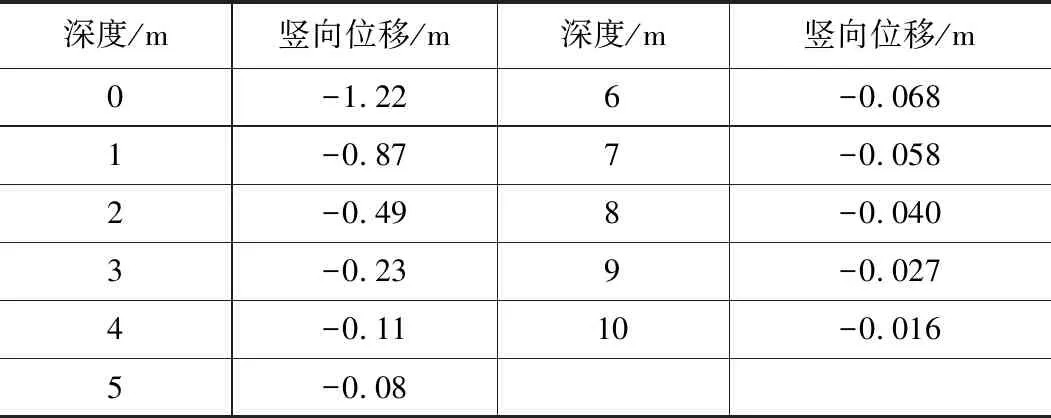
土体竖向位移数据汇总表(300 T·m) 表3

为更加直观，将表3中的数据绘制成变化曲线，如图6所示。

图6 土体竖向位移随深度变化曲线(300 T·m)

根据图6可知，随着深度的增加，土体竖向位移逐渐衰减。竖向位移在 5.5 m深度内衰减幅度较大，在 5.5 m以下深度衰减幅度急剧减小。

通过分析表3中数据可知，以地表夯沉量 1.22 m的5%即 0.061 m的计算点深度为强夯有效加固深度的界限值，对表3使用内插法，可得到强夯有效加固深度约为 6.71 m。

4.3 不同夯击能模拟结果综合分析

本文仅选用了150 T·m和300 T·m的模拟结果，其他夯击能分析原理和过程基本一致，直接引用其模拟结果进行以下分析。

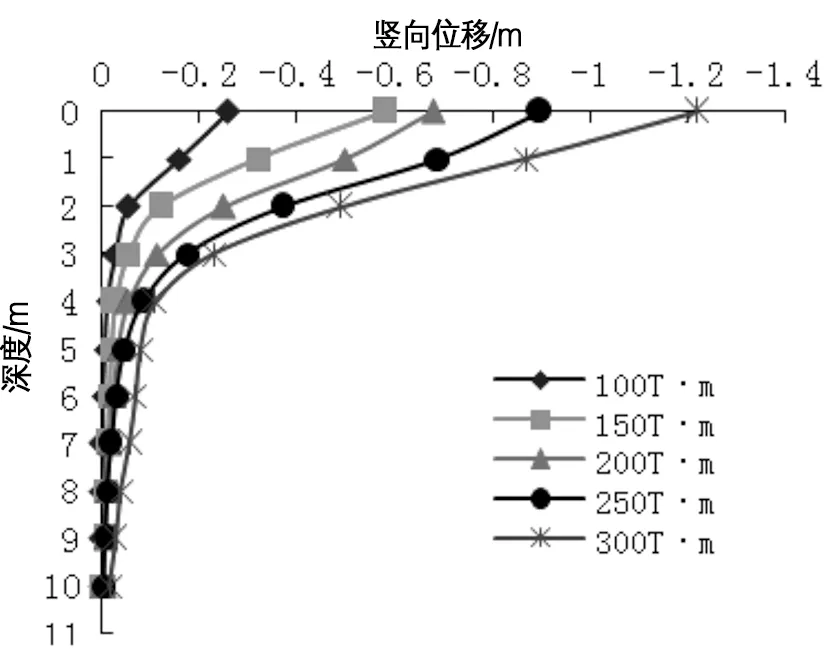
图7 不同夯击能竖向位移随深度变化曲线

从图7中可知，同一深度处的竖向位移随着夯击能的增大而增大，并且在 4 m深度内，土体中竖向位移急剧变化，说明此深度范围内土体受不同夯击能的影响较明显。

通过以上分析，得到不同夯击能的有效加固深度如表4所示。

夯击能与有效加固深度关系表 表4

通过表4可知，强夯的有效加固深度随着夯击能的增大也随之增大，根据表4的数据绘制有效加固深度曲线图并得出拟合曲线，如图8所示。

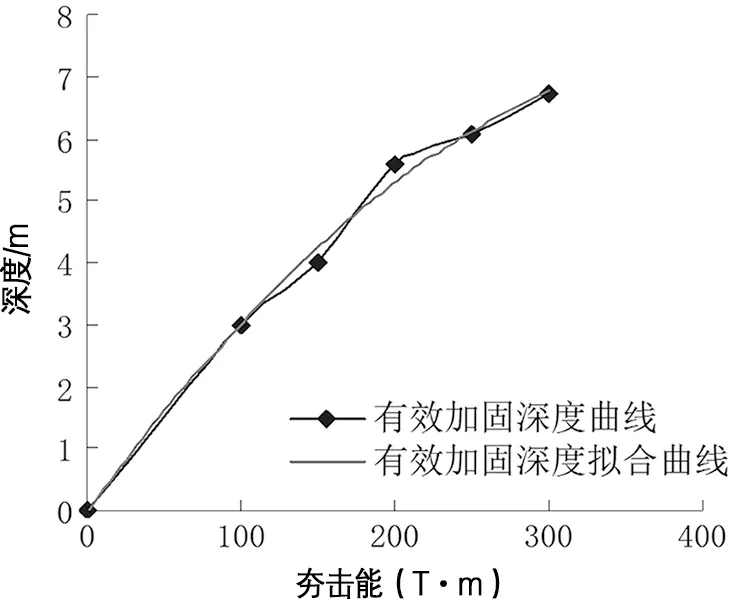
图8 有效加固深度曲线及拟合曲线

根据拟合曲线，通过计算分析可以得到强夯有效加固深度的回归方程为：

H=-4×10-5E2+0.0334E-0.0346

(13)

式中：H为有效加固深度；E为单击夯击能。

5 工程实例分析

本文选取某安置小区强夯工程(夯击能为150 T·m)的原位测试和室内试验数据进行分析，该项目地基土为素填土，主要成分为碎石土、砂土，局部含黏性土。

为进一步验证数值模拟的正确性，本节将通过分析强夯前后地基土的动探击数和压缩模量变化得出实际工程的有效加固深度，同时将夯击能代入回归方程得到计算的有效加固深度，将两者进行对比，分析是否存在差异。

5.1 动力触探试验

为了确定素填土层加固效果，在强夯前后分别进行了动探试验，其统计结果如表5所示。

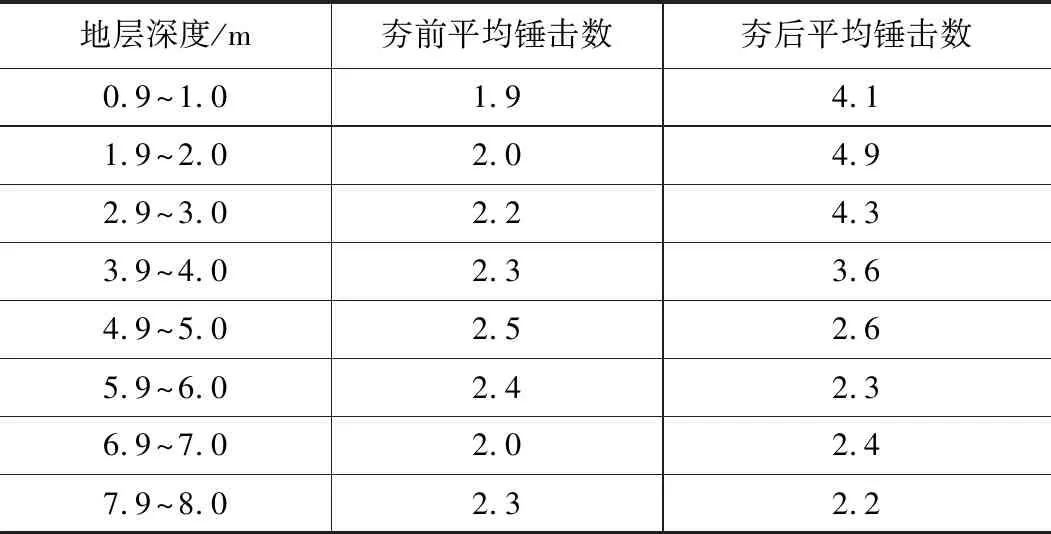
强夯前后地基土动探击数统计表 表5

根据表5作出动力触探N-H曲线图，如图9所示。

通过表5和图9可知，地基土表层深度1 m范围内因存在比较松散的浮土，并未达到最大动探击数。而深度接近 2 m时，动探击数最大，说明此深度加固效果最好。通过对比强夯前后的动探击数可以发现：夯后动探击数是夯前动探击数的1倍～2倍，1 m～5 m深度范围内动探击数变化显著，说明此深度内加固效果最好；而 5 m以下击数交替变化且相差不大，说明加固效果不显著。综上所述，地基土的有效加固深度约为 5 m。

图9 N-H曲线图

5.2 室内土工试验

通过钻探取样，得到强夯前后室内土工试验数据，以压缩模量为例进行分析，如表6所示。

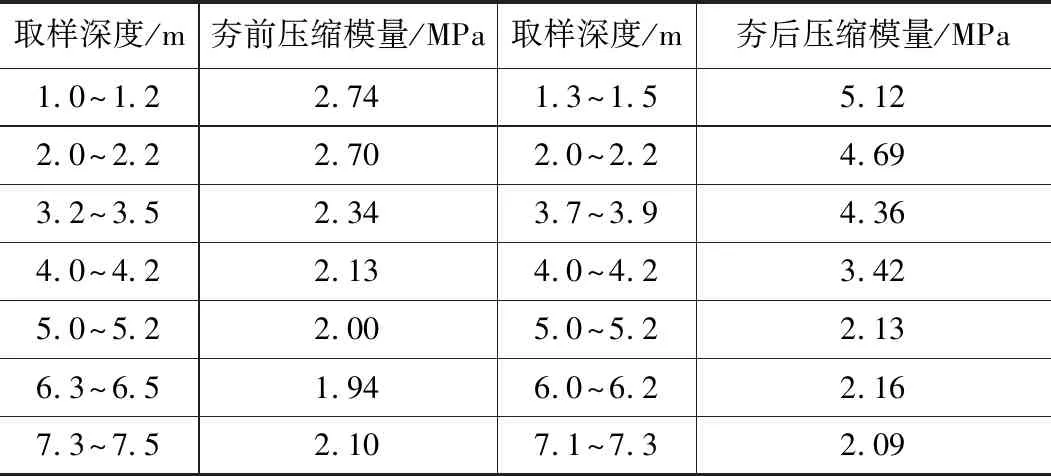
强夯前后压缩模量变化统计表 表6

根据表6作出强夯前后压缩模量随深度变化曲线，如图10所示。

图10 强夯前后压缩模量随深度变化曲线

通过表6和图10可知，5 m深度内土体强度得到了显著提高，5 m深度以下土体压缩模量在强夯前后变化不明显。强夯前后土体的压缩模量在约 5 m深度处基本一致。综上所述，地基土的有效加固深度约为 5 m。

根据以上试验数据综合分析可知，某安置小区强夯工程(150 T·m)实际的加固深度约为 5 m。现将夯击能E=150 T·m代入回归方程：

H=-4×10-5E2+0.0334E-0.0346

计算得到加固深度H=4.1 m。

由于该公式是根据单次夯击能数值分析所得，而实际工程中需经过多次夯击，因此根据回归方程计算的结果较实际工程要稍小，说明数值模拟的结果是基本准确的。

6 结 论

本文主要通过数值模拟分析方法对填土地基强夯有效加固深度进行了研究，并与实际工程进行了比较，得到了如下结论：

(1)以数值分析理论为基础，运用ANSYS/LS-DYNA软件模拟强夯精度较高，能得出地基中各点的动反应数据，具有较高的可靠性，对强夯设计施工具有参考价值和指导意义。

(2)针对不同夯击能，同一深度处的竖向位移随着夯击能的增大而增大，并且在 4 m深度内，土体中竖向位移急剧变化，说明 4 m以内土体受强夯影响较明显。

(3)强夯有效加固深度的回归方程为：

H=-4×10-5E2+0.0334E-0.0346

(4)本文结合工程实例，综合分析了强夯前后地基土的动探击数和压缩模量的变化，得出实际工程的有效加固深度，并与数值模拟得到的加固深度进行对比，根据回归方程计算的结果较实际工程要稍小，说明数值模拟的结果是基本准确的。