带形状参数的双三次G1连续DP曲面

李尚蔚，金虹媛，程晓旭

曲面拼接问题是曲线曲面设计的一个基本问题.经典的曲线曲面包括Bezier曲面、NURBS曲面等，英国几何设计专家Ball提出一种有理三次曲线，被称为Ball曲线.该曲线有类似于Bezier曲线的一些性质，且在保形上以及在求值和升降阶计算上优于同次Bezier曲线；进一步研究结果有 Wang-Ball曲线［1］和 Said-Ball曲线［2］，前者虽然具有线性计算时间复杂度，但却不是全正基（Normalized Totally Positive，NTP）生成的，后者虽然是由NTP基生成的，但其计算时间复杂度却不是线性的，但是有理分式的引入又带来了诸多缺陷，如计算复杂、求积分不方便、求导次数增加等［3］.基于该问题，Delagado和Pena提出了一种新型参数曲线［4］，被学界称为DP曲线，该曲线不但在数值计算上具有稳定性、在算法上具有线性的计算时间复杂性而且是由具有保形性的NTP基生成的；但是DP曲线缺少形状参数调整的功能.为了达到调整形状的效果，可通过设置形状参数来构建形状可控的曲线曲面［5］.本文以带形状参数的三次DP曲线为基础，运用张量积方法构造带形状参数的DP曲面，推导出G1连续条件，给出了一个可以自由调节曲面的方法，使曲面调节更为灵活.

1 带形状参数的DP曲面

1.1 带形状参数的双三次DP曲面的定义

定义1 给定4个控制顶点Pi∈Rn（n=2，3；i=0，1，2，3），对于t∈［0，1］，定义曲线为含形状参数α，β的三次扩展DP曲线，简称带形状参数三次DP曲线［5］.

定义2三次多项式基函数Di(t)

其中，参数α∈［-0.5，1］，β∈［-1，1］，当参数α=0，β=0，该曲线退化为三次DP曲线.

1）曲线W2(t)、W1(t)与满足G0拼接，位置连续的充要条件W1(1)=W2(0)，即b3=p0.

2）曲线G1连续条件，若两条带形状参数的三次DP曲线W2(t)、W1(t)不但满足位置连续，而且在拼接点处具有同向的一阶导矢，即给定 4×4 个控制网格顶点Pi,j（i,j=0,1,2,3），运用张量积方法构造带两个定义3参数的双三次DP曲面

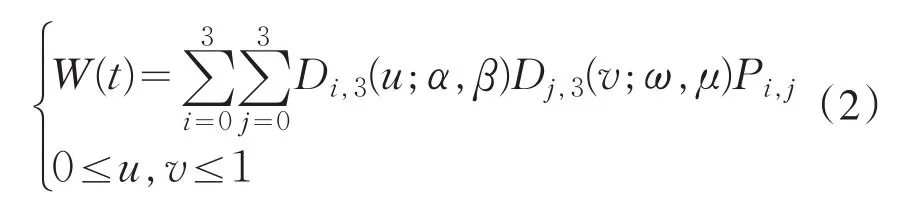
是 [0,1]×[0,1]上的带参数DP曲面，式（2）中形状参数分别是α，β，ω，μ.α,ω∈ [-0.5,1]，β,μ∈[-1,1]，其中，Di,3(u;α,β)，Dj,3(v;ω,μ)是（1）中所定义的基函数.

1.2 带形状参数的双三次DP曲面的G1拼接条件

带形状参数的双三次DP曲面为

首先要求满足G0连续条件，即

然后要求满足G1连续条件，即要求曲面片在拼接边界处有公共的切平面，曲面片在边界上的法矢方向是连续的.因此，

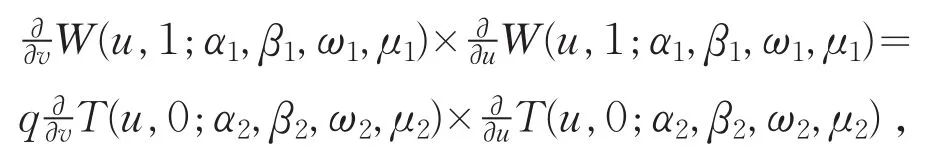
式中，q为大于0的常数.

计算曲面片的跨界切矢，并将式（3）代入得

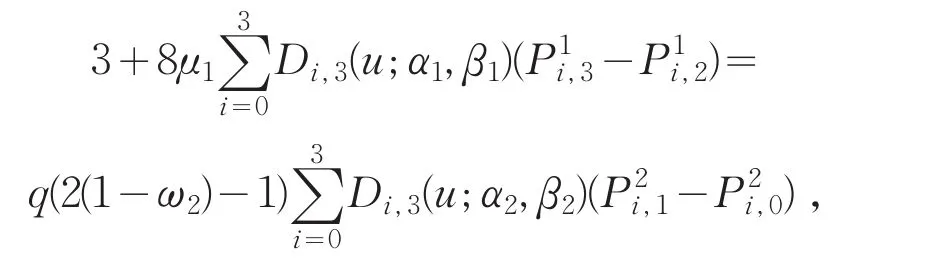
因此，当2张相邻的带参数三次DP曲面W(u,v;α1,β1,ω1,μ1)与T(u,v;α2,β2,ω2,μ2)满足以下条件且同时成立时:

W(u,v;α1,β1,ω1,μ1)与T(u,v;α2,β2,ω2,μ2)在公共边界处满足G1连续拼接条件.

1.3 带形状参数的双三次G1DP曲面拼接步骤

以带参数三次DP曲面u-u方向的G1连续拼接为例，G1连续拼接步骤为:

步骤1:任意给定一个初始曲面W(u,v;α1,β1,ω1,γ1)和控制网格顶点Pi,j.

步骤3:任意给定形状参数ω2和常数f＞0，然后在步骤2的基础上根据（4）可得出曲面和控制网格顶点

步骤 4:任意给定曲面T(u,v;α2,β2,ω2,μ2)剩余的控制顶点和（i=0，1，2，3）形状参数可以随意给出，这样W(u,v;α1,β1,ω1,μ1)与T(u,v;α2,β2,ω2,μ2)在公共边界处实现的G1连续拼接.

带形状参数的双三次DP曲面光滑拼接效果图如图1所示.

图1 带参数三次DP曲面G1连续拼接

2 数值实例

图2 函数z=sin的图形

图3给出了“摇椅”曲面造型的实例.在工业设计上，分别生成摇椅底部和摇椅靠背两部分，图3（a）摇椅底部是以256个点为基础构造DP曲面，图3（b）摇椅靠背是以384个点为基础构造DP曲面，然后进行拼接形成图，图3（c）为摇椅曲面.

图4给出了“床单平铺面”曲面造型的实例.分别以床单的4个部分面，总计4096个点，构造DP曲面，还原床单平铺图.

图3 摇椅曲面造型图

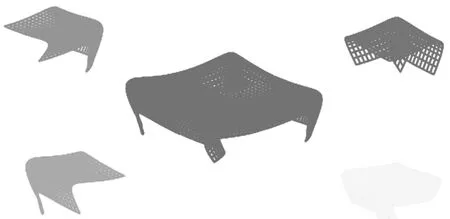
图4 床单平铺图

3 结论

本文构造了一种带形状参数的三次DP曲面，分析了该曲面的基本性质，该曲面不仅保留了Bezier曲面的类似的形状，同时满足了具有形状可调性，而且研究了满足一定条件时，曲面可达到G1连续，数值实例表明了本文方法的有效实用性，可以用来设计不同的曲面.