复杂本质安全电路容性放电引燃特性研究

王振龙，吴冬妮

（凯里学院 大数据工程学院，贵州 凯里 556011）

本质安全电路的火花放电是由于电路在运行过程中触点开闭或绝缘损坏造成的短路而引起的，放电的过渡过程极短，放电产生的火花能量是引爆可燃性气体的有效能源[1-4]。已有的研究成果都是针对单纯的电阻元件、电感元件或者电容元件的本质安全性能进行试验研究得到的，工程设计人员利用点燃曲线来判定电路的点燃能力，为避免复杂的试验验证提供了可行性。本质安全电路中，电感元件和电容元件同时存在的情况是经常出现的[5-6]，且由于分布参数(分布电感、分布电容)的存在，严格意义上的纯电感电路或者纯电容电路是不存在的。由于单一性质电路(纯电感电路等)的放电过程各不相同，其临界点燃曲线也是互不关联，因此不能从这些临界点燃曲线来判断出复杂电路的本质安全性能[7-11]。为此对复杂本质安全电路的火花放电过程、放电的点燃能力以及评价方法进行研究。

1 电感-电容电路的一般形式

通常将集中电感元件和集中电容元件并存的电路定义为复杂本质安全电路，电感与电容元件共存电路如图1。电路在工作状态下，电容元件和电感元件都有能量的存储，这些能量在发生故障时将会释放到放电间隙而发生危险，因此研究电感、电容元件共存电路的火花放电原理对保证电路的本质安全性能十分重要。图1电路中BK为放电间隙，其位置设置代表了电路故障发生火花放电的一般情况。在触点断开的过程中，由于转换方式、储能元件参数的不同，放电的性质和过程也是不同的，因而影响到电路元件中存储能量向放电间隙释放的程度。在电路参数一致的条件下，不同的放电形式的点燃能力也是不同的。

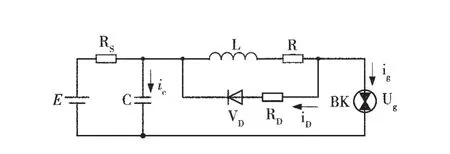
图1 电感与电容元件共存电路

分析电路的放电过程来看，当电路参数不满足振荡条件时，可将电路转化为简单的、单一元件的放电形式来研究。这种放电机理和过程比较简单，此处不做分析。

当电路中的电感元件和电容元件的参数满足振荡条件时，可以预见到，此时的火花放电过程将变得非常复杂，元件参数、元件的初始状态以及火花产生的环境等诸多因素，都会对放电的过渡过程和火花的点燃能力产生影响。由于火花试验装置本身对试验参数的限制[12-13]，使得这类电路的试验研究变得非常困难，试验过程及结论在可以查阅的文献中也鲜有提及。

2 电容性点燃的放电特性

图1中的电感元件及其并联的泄放二极管回路可由能量等效方法折算为单一的等效电感，将图1的电路进一步简化，混合本质安全电路的一般形式如图2，图中包含等效电感和电容2个储能元件。

图2 混合本质安全电路的一般形式

电容电感复合电路发生容性点燃时的电弧电压保持最小建弧电压基本不变[14-16]，由克西霍夫定律得图2的电路方程：

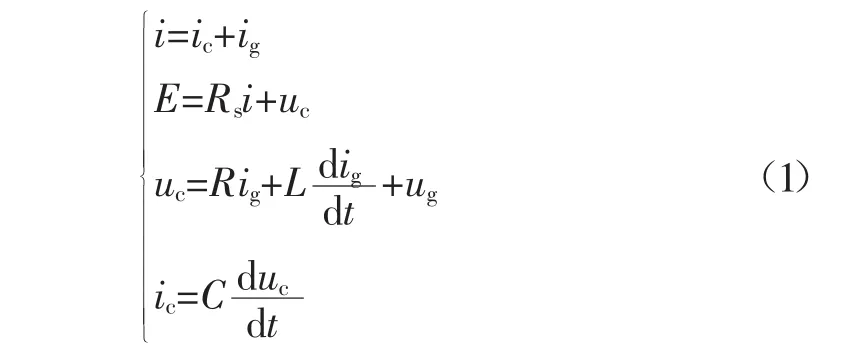
由式（1）得的二阶微分方程：

式中：E、i为电源的电动势和电流；uc、ic为电容C上的电压和电流；ug、ig为泄放二极管上的电压和电流；t为时间；Rs为电源内阻；R为等效电阻；C为等效电容；L为等效电线。

当B＞（A/2）2满足的条件时，电路处于振荡状态。对于含有较大电感的电路，电弧能量主要来自电感，而且LC谐振回路本身具有很高的阻抗，因此，电源对电弧能量的贡献可以忽略，电阻RS可以视为无穷大。进而得到谐振条件：

微分方程的通解：

3 电容为储能元件谐振电路模型

在电容元件的数值相对电感元件较大的条件下，如果发生触点的闭合，则电路状态的转换伴随着以电容元件为主的放电现象。

3.1 放电电流模型的建立

电容C在放电前已经被充电到电源电压E，在放电初始的瞬间，可以认为uc（0）=E；而此时电感元件中流过的火花电流为0，电路中电容为唯一的储能元件。

确定系数c1：

当 t=0时，由式（4）得到：

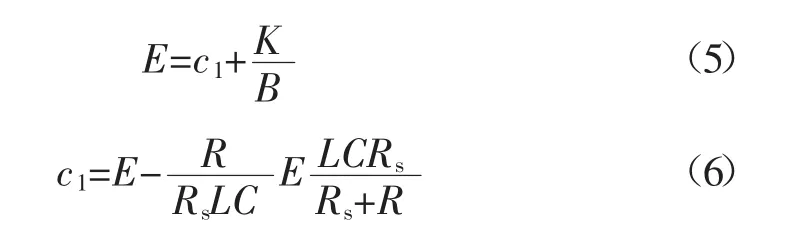
化简得：

确定系数c2：

当t=0时，电容元件中流过的火花电流为0，因此 u′c=0。由式（4）得：

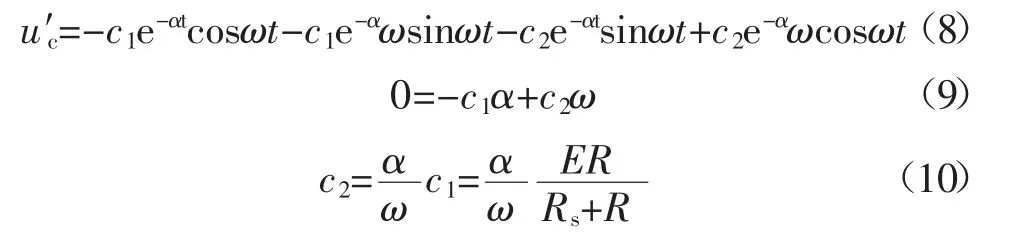
由式（1）得：ig=i-ic，i=（E-uc）/Rs，ic=Cu′c，从而得到放电电流的函数表达式为：

考察式（12）可以看出，表达式的前一项与电源电压、电源内阻和电路电阻有关，因此这部分电流是从电源流向放电间隙的那部分火花电流；表达式的后一项与电容、电感等元件参数有关，是放电电流的主要组成成分。

3.2 放电电流模型分析

满足谐振条件的电感-电容混合电路闭合时的放电电流模型如式（12）。表达式的前半部分为电源对放电电流的贡献，后半部分电流大小以及变化规律是由电容元件和电感元件决定的，表达式的参数构成也反映了放电电流的构成与实际情况相符合。

1）电源对放电电流的影响。由于电感—电容电路在电路断开过程中放电的复杂性，因此难以从放电电流的表达式判断其极值的大小。可以借助仿真软件的帮助来分析对比电感-电容电路放电的规律。复杂电路放电电流仿真波形如图3（电路参数：E＝18 V，Rs=R=30 Ω，L=1 mH，C=6 μF）。在图3 的仿真曲线中，实线为电弧电流的完整波形，虚线为忽略式（12）中前1项后，仅由后1项得到的放电电流波形。从图3中实线的仿真波形可以看出，电弧电流是从0开始急剧上升，在时间左右达到峰值。而后，放电电流随时间的增长而下降，下降速度相对上升阶段明显减慢，虚线的下降速度略大于实线的下降速度。在时间左右，二者的放电电流值几乎相等。由于电感元件的存在会限制电流的变化速度，电流的上升速度和电容、电感元件本身的特性有关。对比两曲线可以看出，电源对电弧电流的贡献很小，基本可以忽略，电弧能量主要来自电路中的储能元件。由于电路所选的电感元件和电容元件参数数值较大，所以放电持续的时间较长。

2）电容元件对放电电流的影响。保持电路其它元件的参数不变（E＝3 V，Rs=R=30 Ω，L=1 mH），改变电容的取值，得到的电容的变化对电感-电容电路放电电流的影响（图略）。随着电容容量的增加，放电电流的上升速度和最大值都迅速增大，由于电弧电压保持最小建弧电压基本不变，所以放电功率呈现随着电容的增大而增加的趋势。

图3 复杂电路放电电流仿真波形

3）电感元件对放电电流的影响。电感-电容混合电路中，假定在电路发生状态切换的瞬间只有电容存储能量的条件下，保持电路中其它元件的参数不变（E＝18 V，Rs=R=30 Ω，C=6 μF），改变电感的取值，得到的电感变化对电感-电容电路放电电流的影响（图略）。随着电感的增加，放电电流的上升趋势放缓，放电电流的最大值也随之减小。电感元件有阻碍通过其内部电流发生突然变化的作用，随着电感的增大，这种阻碍作用势必得到加强，因此电流的上升趋势和最大值将呈下降的趋势。

3.3 放电功率模型的建立

单一电容元件储能的复杂电路（电路中同时存在集中电感元件）在故障状态下的放电瞬变过程中，在火花形成的初始阶段即形成固定的火花电压ug=11 V，在触点接触的瞬间到建立固定火花电压的持续时间非常短，因此可以认为这个固定的火花电压是瞬时建立的。

火花的瞬时功率P为：

将式（12）代入式（13）即可得出功率表达式。

火花的平均功率Pm为：

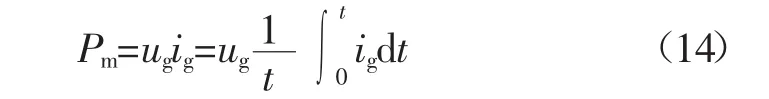
将式（12）与代入式（14）得：

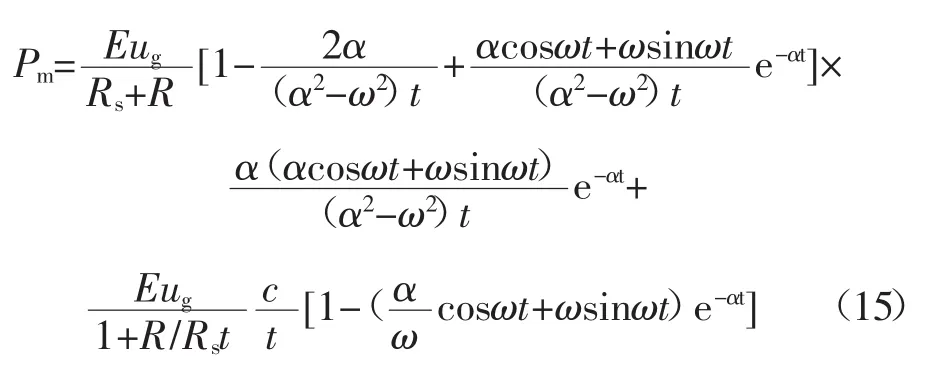
3.4 放电功率模型分析

火花的瞬时功率与放电电流一样，是确定复杂电路的安全性能很重要的依据，反应了电路储能元件在故障时的点燃能力。

为了研究电路中储能元件参数的变化对放电功率的影响，首先改变电路中电容元件的大小，同时保持电路其它元件的参数不变 (E＝18 V，Rs=R=30 Ω，L=1 mH)，得到的电容变化后放电功率对比（图略）；然后改变电感元件的大小，同时保持电路其它元件参数不变(E＝18 V，Rs=R=30 Ω，C=6 μF)，得到的电感变化后放电功率对比图（图略）。

从仿真波形可以看出：放电火花的功率随着电容元件参数的增大而增大，而且电容参数越大，功率的增加越大，这是因为电容中存储能量的不同而引起放电功率的变化；放电火花的功率随着电感元件参数的增大，其放电功率反而呈下降的趋势，这是因为电感越大，对电流的阻碍作用越大，能够减缓电路能量的释放速度。

4 结语

1）分析复杂本质安全电路放电的原理和过程，得到了混合本质安全电路的一般形式。当电路参数不满足振荡条件的情况下，可将电路转化为简单的、单一元件的放电形式来研究。当电路中的电感元件和电容元件的参数满足振荡条件时，通过数学分析得到了谐振电路容性放电条件下的放电电压、放电电流和放电功率的计算模型。

2）复杂电路火花放电的能量主要来自电路中的储能元件，电源电压对放电电流、放电电压的影响可以忽略。

3）满足谐振条件下的容性点燃过程中，随着电容容量的增加，放电电流的上升速度和最大值都迅速增大，火花放电功率也呈现增加的趋势，而且电容参数越大，功率的增加越大，所以电容容量是影响火花放电的主要因素。

4）随着电感感抗的增加，放电电流的上升趋势放缓，放电电流的最大值也随之减小，其放电功率也呈下降的趋势，电感越大，对电流突变的阻碍作用越大，能够减缓电路能量的迅速释放，有利于提高电路的本质安全性能。