一种简化的16QAM软解映射算法∗

兰 霞

（中国西南电子技术研究所 成都 610036）

1 引言

随着卫星和天线技术的发展，卫星影像的分辨率不断提高，海量数据需要传输。然而，每个通信设备的可用带宽是有限的，面临如此庞大信息量的传输需求，频谱资源变得十分宝贵，频谱利用率需要大幅度提高。为了解决信道带宽有限和海量数据传输量之间的矛盾，正交幅度调制（QAM）综合了ASK与PSK的优点，有效缓解数传设备中带宽受限的矛盾，其中，高阶调制方式16QAM一个码字可以携带4bit的信息，在相同带宽的情况下能够有效提高频谱利用率，因此，16QAM调制方式被广泛应用于卫星数传系统中［1～3］。

高阶调制方式可以提高信息传输率，但是采用高阶调制方式的数传系统对于信道的质量要求很高，需要较高的信噪比（SNR）才能够获取令人满意的通信质量，为了克服系统性能对于信道质量的强依赖性，卫星传输领域中往往将高阶调制技术与信道编码技术相结合，既能够获得较高的编码增益，又能够有效地提高频谱的利用率，大大改善通信性能，达到传输高质量海量数据的目的，保障数据的可靠传输。空间咨询委员会（CCSDS）标准推荐的信道编码技术低密度奇偶校验码LDPC7/8是接近香农容量的好码，由于其奇偶校验矩阵的稀疏性，可以克服计算复杂度的问题，具有高速译码能力，可以改善系统的传输效率，便于硬件的实现［4～8］，但是在LDPC迭代译码时需要信号比特的“软信息”输入，即解调之后的软输出数据，而不是简单的硬判决输出。“软信息”的优劣对于整个系统的性能起着关键性的作用，错误的“软信息”会导致译码结果错误，不能够实现信道纠错码的功能。对数似然比（LLR）算法是用于高阶调制方式下求解软信息的常用算法，该算法公式中涉及较多的指数与对数运算，运算量大复杂度高，不适用于工程实现，因此，简化16QAM高阶调制方式下的软信息求解算法是十分必要的。

本文提出了一种简化的16QAM软解映射算法，该算法根据接收信号在单位坐标系中的幅度值进行简单的加法和减法运算，实现对16QAM解调信号4个bit的软判决。比较传统的对数似然比LLR算法，采用本文提出的简化算法可以大大降低运算复杂度，便于FPGA实现，满足16QAM调制方式下LDPC译码性能要求。

2 一种简化的16QAM软解映射的算法实现

2.1 16QAM高阶调制方式

高阶调制方式16QAM是一种正交幅度调制方式，将两路独立的IQ信号用两个相互正交的载波调制而成，在复平面上的表达式为

其中，sI和sQ分别为调制信号的I路分量和Q路分量，(sI，sQ)的大小决定了调制信号16QAM在复平面星座图中的坐标点，方形星座图一般采用格雷码映射方式［9～10］，如在16QAM调制方式中，每一个符号4bit中有两个bit是坐标象限一致的，常用的16QAM星座图映射如图1所示，星座图中的符号对应的比特从高位到低位为(b0b1b2b3)。

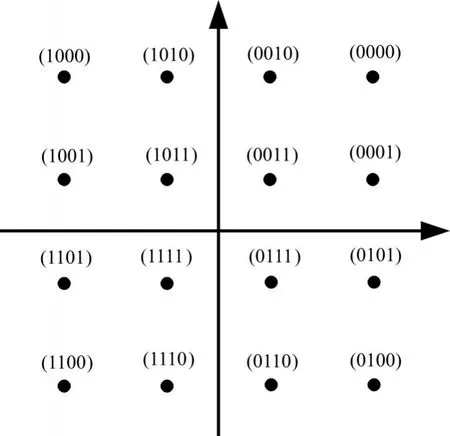
图1 16QAM调制信号星座图

从上述星座图可以看出，采用16QAM高阶调制方式，星座图中的每一个符号可以携带4个bit信息，在带宽受限的条件下，采用16QAM高阶调制方式可以提升传输速率，满足卫星数据量大的数传要求，频谱率得到大大的提高。

经过高阶调制16QAM调制的信号是通过高斯信道之后，接收端接收端接收的信号为

其中rI和rQ分别为接收信号的I路分路和Q路分量，接收信号是由发送端的信号s加上方差为σ2的高斯白噪声n之后的信号，即

式（3）中的噪声变量n也同样有I路和Q路两个分量，两个分路是独立同分布的随机变量。

2.2 LLR算法

接收端将接收信号解调之后只是得到了IQ两个符号的解调信息，在复平面星座图上为坐标点(rI，rQ)，然而后续的数据处理需要知道16QAM调制方式携带的4个bit的软信息，根据最大后验概率准则，16QAM映射比特bi的对数似然比函数值［11～12］为该比特的软信息值，具体定义为

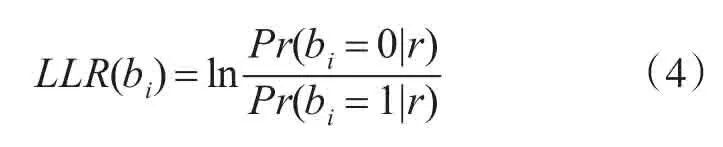
在高斯白噪声信道中，发送信号的每一个码字是等概率的。对于每一个比特分量bi，它的发送信号集分为两个部分，其中是bi为0对应发送信号的集合，是b为1对应发送信号i的集合，数学表达式如下：

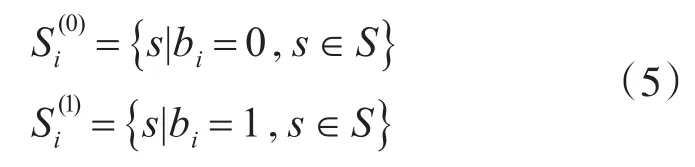
图2 16QAM星座图中各个比特对应和的集合

与图1中16QAM星座图映射相对应的Si(0)和两个集合分布图如图2所示，图2中的4张图分别对应16QAM调制方式中的4个比特(b0b1b2b3)，

根据概率计算公式，式（4）中比特bi的对数似然比为

式（6）需要大量的指数运算过程，为了减少指数运算的复杂度，利用近似准则［13～15］式（6）可以计算为

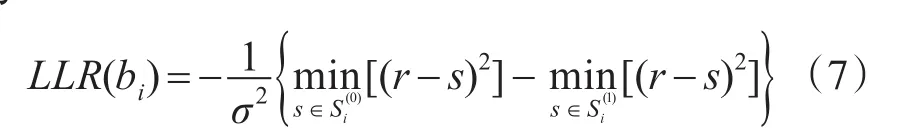
相比于计算式（6），式（7）简化了指数运算的复杂度，但是在计算每一个比特的LLR对数似然比值的时候，都要通过计算接收信号的幅度值与星座图中坐标点的距离值，并且寻找包含0点集合和包含1点集合中的最小值，可以看到，该方法的计算量和计算复杂度也较高，不适合工程应用。

2.3 简化的16QAM软解映射算法

在工程实践应用中，FPGA实现时需要简单快捷的运算方法，式（7）中的运算公式还是过于复杂，因此，本文提出了一种简化的16QAM软解映射算法。

从图2中可以看出，16QAM星座图中的各个比特的各个取值集合有一条或者两条明确的分界线，这些分界线有坐标轴或者垂直于坐标轴，垂直于坐标轴的分界线设置为 x=±c和 y=±c，c点在16QAM星座图中的分布图如图3所示，c的值在下文会分析如何求解。

图3 c点在16QAM星座图中的分布图

同样地，根据比特b2和b3在16QAM星座图中的分布特性及其对称特性，利用分界线的位置关系，可以定义比特b2和b3的软信息计算公式如式（9）：

其中，参数λ是相减运算的幅度补偿。由于在高速数传工程中需要采用高阶调制方式高码率的信道编码方式LDPC编码等，然而，LDPC迭代译码性能的高低依赖于接收信号的软信息，因此，幅度相减运算之后，使得幅度有一定的偏差，会造成译码性能受到很大的影响。实际上，在工程应用中λ取整数时，也就是幅度值简单的几次累加而已，运算简单方便。

由于坐标轴的对称性，可以只观察第一象限，分界线点c的值是第一象限的4个比特点的中心点即四个点的均值，如图4所示，则c=(rI1+rI2+rQ1+rQ2)/4。

图4 星座图中第一象限点的分布图

然而，在实际的工程项目中，星座图中的点是受到噪声污染的接收信号r=s+n，其中n是均值为0方差为δ的高斯白噪声，根据高斯白噪声的0均值特性，见推导公式（10），同样可以通过接收的信号幅度做一个统计分析求均值即可得分界点c的值。

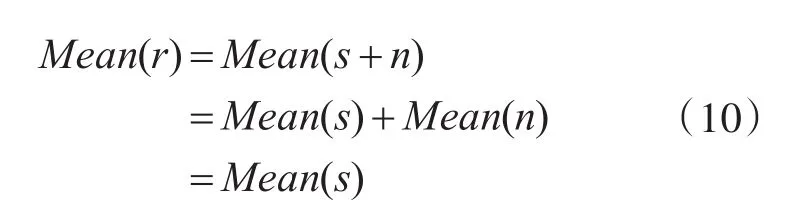
根据式（10）可以看到，虽然接收信号受到了噪声的污染，但是采用该信号作为原始信号s的均值估计是可行的，因此，在实际的工程应用中，直接统计接收信号的均值就可以估算分解点c的值。具体工程实现框图如图5所示。

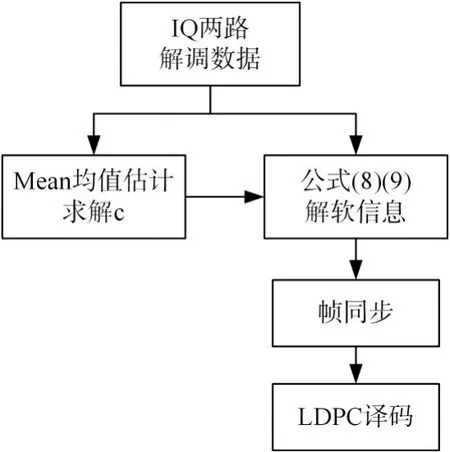
图5 16QAM调制方式下LDPC译码流程

总之，本文提出了一种简化的16QAM软解映射算法，该算法根据接收信号在单位坐标系中的值进行简单的加法和减法运算，实现对16QAM解调信号的4个bit的软判决。比较传统的对数似然比LLR算法，采用本文提出的简化算法可以大大降低运算复杂度，便于FPGA实现，并且满足16QAM调制方式下LDPC译码性能要求。

3 实验与分析

3.1 复杂度分析

高阶调制方式可以提高信息传输率，但是采用高阶调制方式的数传系统对于信道的质量要求很高，为了克服系统性能对于信道质量的强依赖性，卫星传输领域中往往将高阶调制技术16QAM与信道编码技术相结合，道编码技术低密度奇偶校验码LDPC7/8是接近香农容量的好码，它在迭代译码时需要信号比特的“软信息”输入，对数似然比（LLR）算法是用于高阶调制方式下求解软信息的常用算法，但是，该算法公式中涉及较多的指数与对数运算，运算量大复杂度高，不适用于工程实现。

然而，本文提出的16QAM软解映射简化算法可以大大降低运算复杂度，采用简单的6次加减法运算就可以计算出16QAM解调信号的4个bit的软信息。与传统的LLR算法及其近似算法比较如表1，从表1可以看出，本文提出的算法大大降低了运算复杂度，减少逻辑运算分析，利于工程实现。

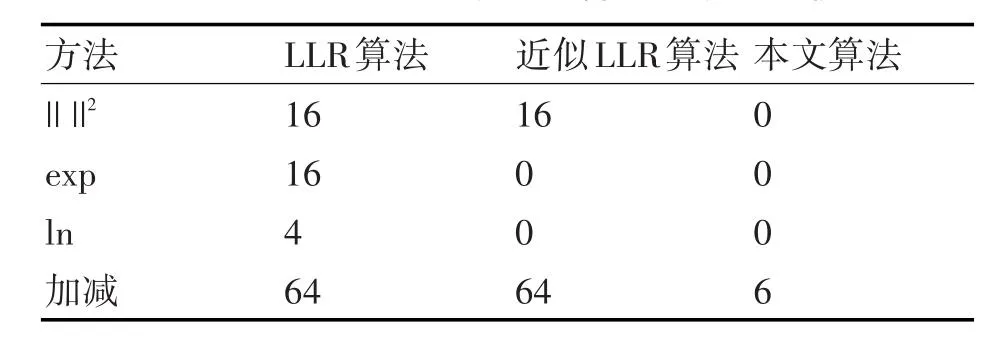
表1 16QAM求解软信息算法复杂度比较

3.2 工程实现

本文提出的16QAM软解映射简化算法已经被应用在工程项目中，如图6，是某个工程项目中16QAM调制方式下LDPC7/8译码结果，在不同的信噪比下的LDPC译码性能的误码率统计值。根据图6的统计分析可以看到，采用本文提出简化算法求解软信息用于LDPC迭代译码，可以满足工程应用中LDPC7/8的译码性能要求。

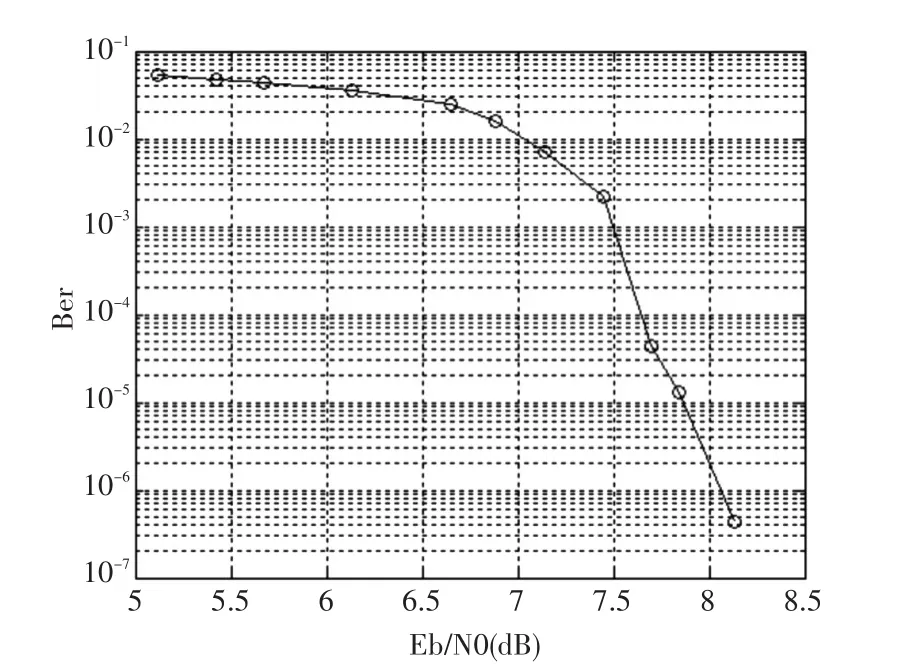
图6 16QAM调制方式下LDPC7/8译码性能统计曲线

4 结语

本文提出了一种简化的16QAM软解映射算法，实验结果表明，该方法用于高速数传工程项目中实现16QAM调制方式下LDPC7/8迭代译码，满足海量数据传输目的，大大提升频谱利用率。该方法能够显著减少16QAM解软信息的硬件资源，并且性能满足高速数传的实际需要，便于工程的实现。