多正交信号水下导航系统位置校准的CRLB研究∗

郭锦标 张 森

（海军工程大学 武汉 430033）

1 引言

随着海洋开发的不断发展，对水下导航定位设备的需求越来越高。基于单信标的水下导航系统由于其实用性和经济性等优势受到越来越多的关注和研究。

多正交信号水下导航系统［1］通过一个信标同时发射一组正交信号，使得接收端接收到信号就可以解算出自身位置，系统由水下的声学设备和船上的信号处理设备及GPS等组成，如图1所示。

由于在布放水下信标时，只能获得信标的概略位置，其在水下的精确位置不得而知。接收端需要获知信标的精确位置，以此修正解算值。信标的位置信息是导航系统位置解算的必须数据，因而通过校准获得水下信标的地理坐标是多正交信号水下导航系统的一项关键技术。

校准航迹的选择直接影响位置估计的效果。国外超短基线系统技术比较成熟，生产设备的公司中，Sonardyne公司采用“⊕”字型的校准航迹［2］，而IxSea公司的Posidonia采用“8”字型的校准航迹［3～4］进行数据获取，至于他们为何选择这样的航行轨迹，我们不得而知。而在国内，最早由唐秋华等［5］提出超短基线定位系统的校准算法，它是将安装校准的三个旋转角度偏差和三个位移偏差等效作参数估计问题，在最小二乘准则下估计各个量的值，并对其进行优化，但其并未提到校准航迹的选择问题。之后的校准研究都是基于这个方法而进行改进，2005年喻敏在研制长程超短基线时提出了校准数据采用航船绕行方式获取［6］，2007年郑翠娥［7］在USBL的水下平台对接应用中提出了校准航迹需要选择绕行半径较大、水深不易过浅的测线。杨保国［8］通过建立校准观测方程，研究方程最小二乘解的唯一性和无偏性，提出了校准航迹需满足一定的尺度和对称性的要求，并且验证了“⊕”字型和“8”字型航迹的可行性。

图1 多正交信号水下导航系统

多正交信号水下导航系统的校准航迹在现有的传统的“⊕”字型和“8”字型中选择，本文通过比较不同航迹的位置估计性能，合理规划校准的路径选择，可以有效提高位置估计的性能。

2 误差模型建立

基于最小二乘准则的位置估计［9］需要先建立观测模型，根据空间测距交会原理得到观测方程为

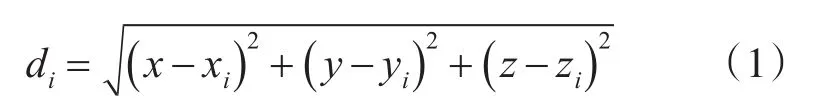
其中，x，y，z为待求的水下信标在大地坐标系下的坐标，xi、yi、zi(i =0，1，...n )为接收端（水听器）在大地坐标系的坐标（n为船测量的次数），di为利用声学方法测出的信标与水听器的距离。

在观测过程中，存在两方面的误差：1）距离测量的误差；2）GPS定位误差。

2.1 考虑距离测量的误差

当存在距离测量误差时，则式（1）应改写为

式中的观测距离误差量ni是直接由距离测量误差带来，实质上距离测量误差是由于使用声学设备测量接收端与发射端之间信号传播的时延误差所致，误差可以看成是零均值的高斯随机变量，si表示实际的观测值。

2.2 考虑GPS测量的误差

接收端的大地坐标由GPS测量获取，在测量过程中也存在误差，因此接收端的位置误差也是影响位置估计的主要误差来源之一。为了清楚分析GPS测量误差的影响，这里先忽略距离测量的误差，即假设GPS测量误差是唯一的误差来源，此时式（1）可以改写为

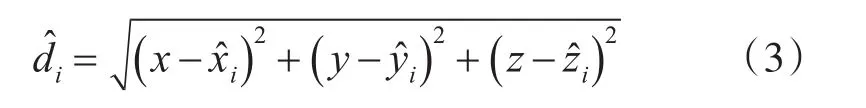
将第i个接收端位置的坐标误差记为

式中 ，xi，yi，zi是接收端的实际位置为GPS测量的位置。同样假设GPS定位误差服从零均值的高斯分布，三个坐标轴方差分别为

对式（3）进行泰勒展开并取其一次项得到

所以可以得到观测距离的误差为

则

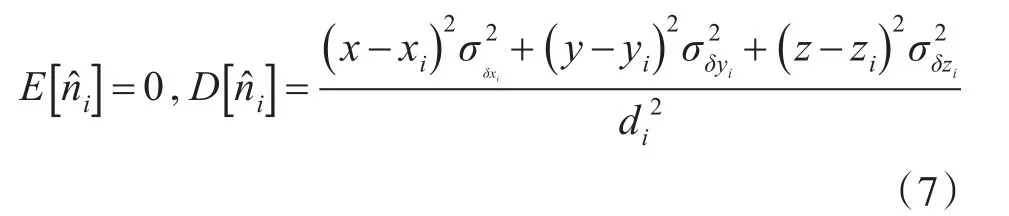
GPS的定位精度水平方向和垂直方向稍有差异，一般垂直方向的定位精度约为水平方向的2～3倍［10～11］，为了后续计算方便，将水平定位精度与垂直方向定位精度近似相等，因此可以得到：

2.3 总误差模型

上面分别讨论了只存在距离测量误差和GPS测量误差时观测方程的建立，实际上，观测方程误差既有来自距离测量的误差，也同时存在GPS的测量误差，所以观测方程的方程应该写为

3 CRLB推导

式（9）可以表达成简洁形式：

式中p=(x ，y，z)为待估计的向量，即水下信标的位置。

假设误差是相互独立的高斯随机变量，则条件概率密度函数p(s|P)为

将式（11）取对数并略去常数项可以得到对数：

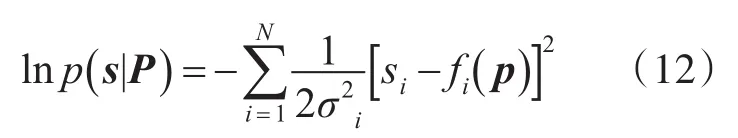
位置估计向量 p的第k个参数（即 pk）的CRLB定义为［12］

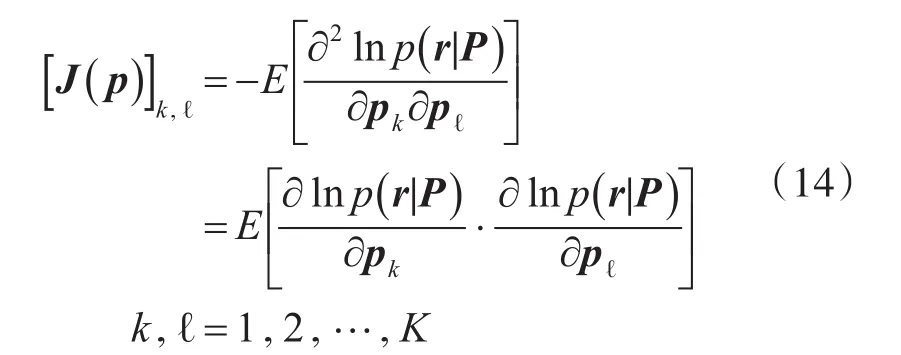
通过数学处理，可以得到费歇尔信息矩阵如下：

根据上述公式，利用矩阵求逆可以得到三个位置坐标估计的CRLB为

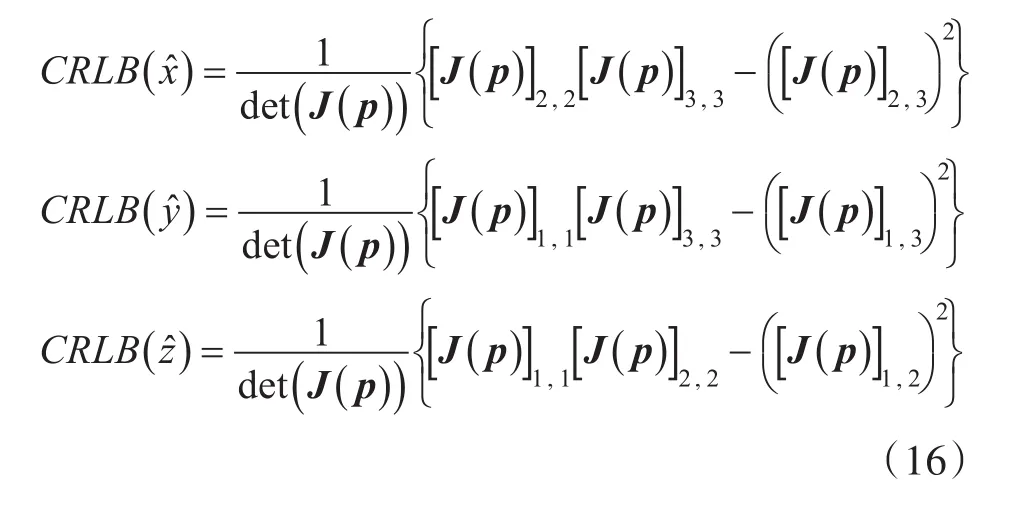
4 CRLB的仿真分析

基于最小二乘的位置估计是一种无偏估计的过程，CRLB作为评价无偏估计性能的界限，能对估计结果的性能做出评估。在引言中介绍过，不同航迹的选择影响到校准结果的性能，目前常用的校准航迹是“⊕”字型和“8”字型，因而可以运用本文推导的CRLB对二者的估计性能进行比较，并结合多正交信号水下导航系统的实际做出较佳校准路径的选择，同时也可以建立CRLB与GPS测量误差及时延测量误差的关系。

4.1 航行轨迹的仿真

仿真“⊕”字型和“8”字型的航行路线，在航行路径上取均匀的观测点用于获取数据。假定海平面深度为0，向下为正方向，船绕着信标航行，两种路径如图2所示。

图2 船的测量点与信标的位置

4.2 位置估计结果的比较

在航迹上均匀取点作为数据测量点，在每个测量点上，检验1000次的测量结果，对水下信标位置估计结果进行性能平均，比较在两种航迹下算法估计的均方根误差，用CRLB作为两种航迹估计性能的检验标准。假设水下信标的真实位置是在测量点的位置误差为GPS的测量误差所致，且x、y和z轴坐标的误差为独立的高斯随机变量，其均值为0，并假设水平定位标准偏差为1.5m；时延测量误差同样为独立的高斯随机变量，其均值为0，标准偏差为10-4s。

根据仿真结果计算这两种航迹位置估计的均方根误差。按照下式计算CRLB的开方:

位置估计的均方根误差（RMSE）按照下式计算:

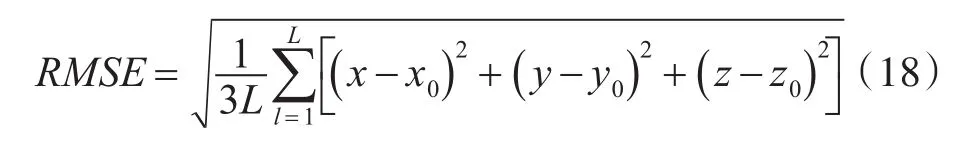
其中L表示在每个测量点上的实验次数。

仿真图中的图例解释如下：

circular-sim表示基于“⊕”字型航行轨迹位置估计的均方根误差模拟结果。

eight-sim表示基于“8”字型航行轨迹位置估计的均方根误差模拟结果。

CRLB1表示基于“⊕”字型航行轨迹位置估计的CRLB计算结果。

CRLB2表示基于“8”字型航行轨迹位置估计的CRLB计算结果。

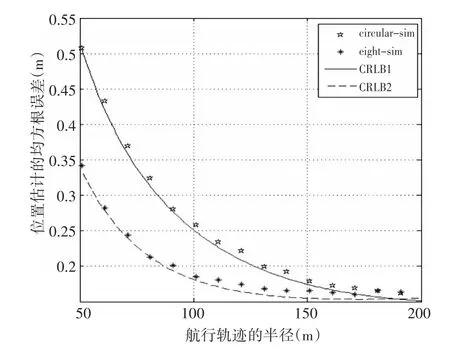
图3 航行轨迹半径与位置估计误差的关系

考虑在航迹上均匀测量400个点，其中“⊕”字型航行轨迹在圆周上均匀取200个测量点，在两条直径线上各均匀取100个测量点；“8”字型航行轨迹在两个圆周上各均匀取200个测量点。从图中可以看出，采用“8”字型航行轨迹位置估计的CRLB计算结果优于“⊕”字型航行轨迹定位，但随着测量半径的增加，两种航行轨迹位置估计的性能差距越来越小，在半径达到200m左右时，“⊕”字型航行轨迹位置估计的CRLB计算结果开始低于“8”字型航行轨迹的计算结果。采用最小二乘的计算方法进行位置估计，估计得到结果的均方根误差可以逼近CRLB，因而我们采用的CRLB计算方法可以用于预测位置估计算法的性能。从这个仿真结果可以指导我们在实际测量中根据测量船航行的半径选择航行路径，使得位置估计的精度理论上尽可能地得到提高。

考虑测量点的数目对位置估计性能的影响。同样比较两种航迹的CRLB计算结果和位置估计的均方根误差模拟结果，鉴于上面比较的航迹半径对位置估计性能的影响，取航行半径为200m，这样航行半径对不同航行轨迹的影响相近。

图测量点数目与位置估计误差的关系

从图中可以看到，采用“⊕”字型航行轨迹位置估计的CRLB计算结果优于“8”字型航行轨迹定位，但这种优势是十分微弱的，所以测量点的数目对两种路径的位置估计影响是一致的。

图5 测量点数目与位置估计误差的关系

在实际测量环境中可能达不到大半径的需求（航行半径在200m以内），且为了降低成本尽量减少测量的次数，所以若要得到较高的位置估计精度，应选择采用“8”字型的航行轨迹。但这种航迹是由两个外切圆组成，完整的航迹需要走过的水域面积是“⊕”字型航行轨迹的两倍。现在我们考虑“8”字型的航行轨迹半径为100m，“⊕”字型航行轨迹半径不变，观察两种航迹对位置估计性能的影响。

可以看出在这种情况下，“⊕”字型航行轨迹位置估计的性能优于另外一种。对于多正交信号水下导航系统，其功能是实现一定区域的水下导航，若船的航行区域过广，也可能会出现接收不到水下信标信号的情况。所以无论水域可航行区域有限，或是出于校准的可实现性考虑，“⊕”字型的航行路径选择优于“8”字型。

4.3 CRLB与系统测量设备误差的关系

水下导航系统用于位置校准的测量设备主要有GPS和声信号传播时延测量仪器，这些设备的误差决定了校准的性能。在位置校准中可以利用CRLB与测量设备误差的关系选择测量设备的参数，从而达到位置校准的精度需求。

选择“⊕”字型的校准路径，航行半径200m，观测在不同的GPS测量误差和时延测量误差下CRLB的趋势，如图6所示。

图6 CRLB与GPS及时延测量误差的关系

通过建立上面的趋势图，可以直观地看出CRLB与GPS测量误差及时延测量误差的关系。当校准技术指标要求达到多大精度的位置估计时，那么就可以在z轴找到对应的的数值，用一个垂直于该数值的面与得到的这个曲面相交，将相交所得的曲线投影至xoy面上，坐标值对应的便是GPS测量误差和时延测量误差的精度要求，因此利用此关系图可以指导选择测量设备的参数。

5 结语

本文采用传统的基于最小二乘原理的方法对多正交信号水下导航系统的信标位置进行校准，主要提出并完成了以下几个工作：

1）建立了位置校准的误差模型；

2）推导了用于评估位置估计性能的CRLB；

3）通过计算机仿真分析，“⊕”字型的校准航迹得到的位置估计结果性能更优；

4）建立CRLB与系统GPS测量误差、时延测量误差的关系。