大展弦比机翼试验随动加载系统研究
李小欢,张蕾
(成都飞机工业(集团)有限责任公司 技术中心,成都 610092)
0 引 言
大展弦比无人机机翼设计技术是长航飞机高空高速设计的关键技术之一,机翼设计的核心是提高飞机的航程、航时,并提供安全高效的力矩特性和升阻特性,使机翼的强度、刚度、安全、寿命等满足设计要求[1]。在机翼的设计中,首先进行外形设计,再通过静力试验结果保证飞行时机翼的弹性变形满足设计要求[2]。对于大展弦比复合材料机翼[3]而言,由于机翼弹性变形大,从而气动特性对飞行安全影响更为严重,在大展弦比机翼设计时,必须考虑复合材料机翼在气动载荷下的弹性变形[4]。
根据国军标提出的研发飞机重要部件必须进行静力试验的要求,机翼试验是获取机翼的力学性能最有效、最可靠、最直接的方式。机翼试验需要将飞机飞行时所受的载荷[5-6](气动载荷、惯性载荷、集中载荷)简化为数量有限的集中载荷,再通过加载系统将加载点进行多级合并来实现各级载荷加载[7-8]。加载系统设计的合理性是决定大展弦比机翼试验成败的关键,尤其是机翼载荷随试验件变形而变化,导致加载点与翼面弦平面不垂直,且机翼的变形越大,载荷的角度偏差也越大[9]。因此,加载点随试验件变形而移动变化是大展弦比机翼试验中不可忽视的问题。
本文针对大展弦比机翼试验任务和加载技术,对机翼受载大变形情况进行加载准确性分析,开发一种适用于无人机大展弦比试验的随动加载系统,阐述该随动加载系统的工作原理,设计、试验和运用等关键问题,以期为类似加载系统提供设计依据。
1 国内外加载系统研究现状
近几年,欧美、俄罗斯、日本对飞机机翼试验的加载方法进行了初步的研究,但公开报道很少,国内进行了不同加载方式的研究。某强度试验室进行了一次该无人机机翼的带外挂飞行试验,采用的常规加载方法,翼尖位移变形的试验结果与理论值误差为-20%。由于加载误差偏大,通过对加载方法的分析得出这种加载设备固定的加载方式运用于小展弦比机翼试验是可行的,但用于大展弦比的机翼试验时,由于机翼变形量大,会产生试验加载载荷与实际飞行状态载荷误差大的情况,且机翼变形越大,载荷偏差也越大。加载误差来源是机翼大变形引起加载方向发生变化,当加载方向与翼面不垂直的时候,加载载荷会向翼面及其垂直平面分解,会造成载荷失真及产生附加力矩,影响试验准确性。在机翼变形后,对加载载荷进行分析发现,F分解为两个力F1和F2,F1为垂直翼面分力,F2为平行翼面分力,如图1所示。通过分析可得,此时用F对机翼进行加载,加载误差大,影响试验的准确性。机翼变形量与加载载荷的关系如图1所示。
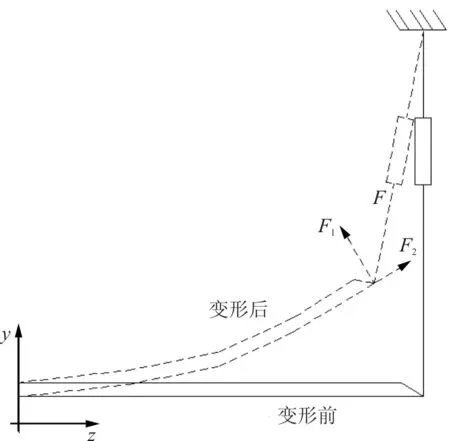
图1 机翼变形载荷分析
通过分析固定加载误差,结合刘兴科等[10]在全尺寸飞机静力试验中,采用简化的特征载荷加载方式,即在100%限制载荷位置保证加载载荷与翼面垂直的预偏加载方法,再次进行了一次飞行载荷试验,试验结果显示翼尖位移变形的误差为14%,加载误差仍然较大。最大载荷预偏分析如图2所示,通过分析受力情况可得,预偏加载从刚开始会产生F1和F2两个分力,会对机翼受载产生影响。此种方法对于小变形加载具有一定的作用,但对于此次试验满载情况机翼变形量为1 250 mm时,若采用特征载荷预偏,会导致从初始加载位置起加载误差大,且加载误差会不断持续和累加,导致加载精度无法保证。

图2 最大载荷预偏分析
陈建国[11]设计了一种高位摆梁随动加载机构(如图3所示),该机构通过位移作动筒推动摆梁摆动实现载荷动态加载,运用于飞机襟缝翼收放功能试验具有很好的效果。并提出这种方法可推广运用于飞机升降舵、方向舵、副翼等操纵面收放功能试验的随动加载系统研究。

图3 高位摆梁随动加载机构
周栋等[12]设计了一种基于杠杆原理的起落架试验随动加载装置,该装置利用杠杆平衡,将正确载荷施加在杠杆的一端,从而消除加载中心移动产生的附加弯矩,该装置特别适合运用于某型飞机主起落架的试验。并指出此机构基于杠杆原理的加载装置解决了随着加载点变化施加垂直载荷引起的附加弯矩问题,已经应用于某型飞机起落架试验中,具有重大的现实意义。
庞宝才等[13]研究了一种可动翼面的随动加载方法(如图4所示),基于力的等效原则,采用单点双作动筒从两个方向对顶来实现载荷的动态变化,且该装置应用于一种民用飞机刚度试验,取得了良好效果。并指出单点双作动筒布置于机翼加载翼面下部,作动筒底部通过底座铰链连接,通过双作动筒收放控制调节保证合力载荷的大小和方向,从而实现载荷实时垂直于翼面加载。

图4 对顶等效随动加载机构
2 加载要求及模拟分析
在机翼试验的加载过程中,为了消除加载误差,最准确的方法是加载方向和载荷大小随机翼变形而实时变化,加载方向要始终垂直于翼面,如图5所示。

图5 加载载荷与翼面动态垂直
本文应用Patran对试验机翼进行有限元模拟分析,建立包括试验件和边界条件的有限元分析模型,对机翼结构受载过程的变形情况进行分析,更直观地呈现机翼结构的弯曲变形,可作为机翼结构强度刚度性能设计的依据,同时可为试验总体设计提供理论支撑,从而避免试验过程中由于机翼变形可能造成的机翼与设备干涉、碰撞、损坏等问题。分析时,将机翼内段与机身连接结构进行约束,用于模拟机身对机翼的支持,在机翼表面施加等值Force用于模拟飞机所受的飞行载荷,通过有限元分析可见,机翼变形示意图如图6所示,机翼满载变形量如图7所示。

图6 机翼模拟变形

图7 满载情况机翼变形
从图6~图7可以看出:机翼整体变形从内段到外端逐渐增大,变形幅度与机翼展向位置呈正相关,机翼翼尖变形量最大,翼尖变形数值为1 250 mm,机翼各肋截面的变形量如表1所示。将飞行载荷下机翼变形量与机翼展向关系近似看作二次曲线,如图8所示。
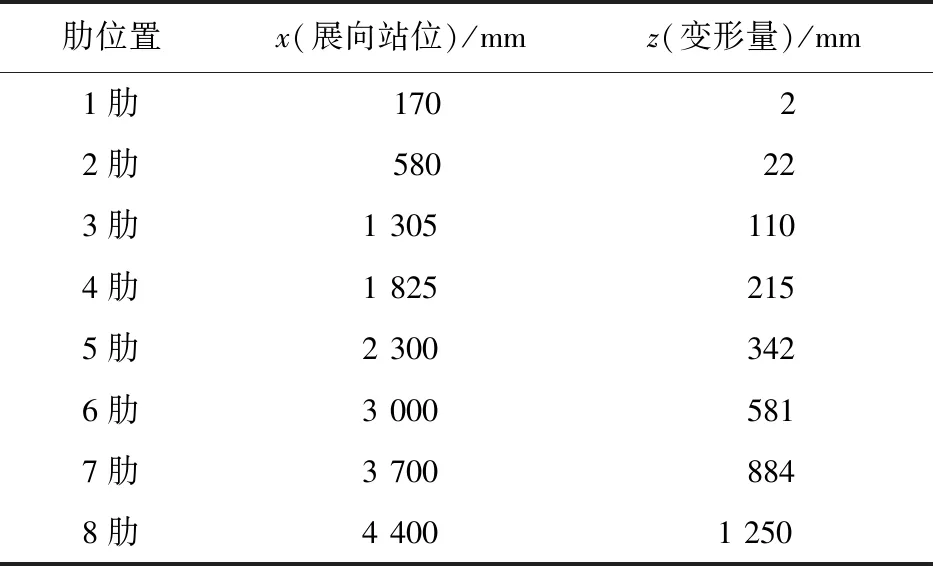
表1 机翼各肋截面的变形与展向站位关系

图8 机翼变形与展向站位关系
假设机翼变形与展向关系近似看作二次曲线时,由二次曲线z=Ax2+Bx+C,得

(1)
二次曲线任一点切线
K=2Axn+B
(2)
二次曲线上任一点切线和法线斜率K′关系:K·K′=-1,所以
(3)
式中:n为试验加载的级数(n取1,2,3,…,n);z为机翼变形后机翼翼尖M点对应的垂直位移;x为M点的展向站位;A、B、C为曲线未知常数;K为二次曲线在M点处的切线;K′为K的垂线,与x相交与N点。
由于该机翼试验时左右机翼为对称载荷,以BL=0处为对称轴线,该二次曲线的对称轴为x=0,所以式中B=0,而该曲线过原点,所以式中C=0,由翼尖M点在各级载荷下展向站位x与z可求得曲线常数A,也可求得直线ON距离。同理通过控制ON距离,实现K′与K实时垂直,从而保证加载过程中翼尖位置加载方向与翼尖弦平面的垂直状态。
3 随动加载方法
针对该机翼试验的翼面载荷加载要求和理论模拟分析结果,结合随动加载系统研究现状,本文开发出一种新的双作动筒推动随动加载系统。该随动加载主要包含两部分内容:一是位置跟踪,二是动态加载。基于计算机辅助设计建立机翼试验数模,从翼面结构和满载典型工况分析其运动范围,结合该试验5%限制载荷级数加载要求,将整个加载分为20个典型的飞行状态点,再建立其随动加载载荷函数,根据每一级采集实测的翼尖变形量计算出随动系统应该调整的位移和角度,保证每一级加载载荷垂直于翼面,从而进行载荷的随动加载控制。该随动加载系统初始位置如图9所示,此时载荷为0,机翼无变弯曲变形。当试验开始进行,随着载荷值级数增加,机翼开始弯曲变形如图10所示。

图9 随动加载初始位置

图10 随动加载弯曲变形
由几何关系计算,此时有函数:

(4)
由式(4)可得
(5)
所以
(6)
式中:β为机翼弯曲变形偏转角度(变量);H为地面位移传感器测量位移值(变量);i为逐级加载级数,为5、10、15~90、95、100共20个数值;L为左侧机翼长度值(常量);x为移动滚轮位移量,即随动作动筒伸缩量(变量);C为机翼安装高度距5 m压梁的距离(常量)。
通过式(6),根据机翼翼尖弯曲变形量在加载载荷下向上弯曲变形实测数据H可逐级计算得移动滚轮移动量x,再通过井架上方随动作动筒伸缩量控制移动滚轮滑动,整个加载系统包括加载作动筒实现了x向的实时位置变化,从而实现载荷方向的倾斜变化,使加载方向实时垂直与翼面,从而实现机翼载荷的随动加载。
4 工程试验
4.1 试验现场
试验现场如图11设计并搭建,试验支持夹具模拟机身对机翼的支持,上部通过六个翼身连接交点与试验件相连,试验支持夹具下部固定在地轨上,在试验件上方搭建井架用于试验加载、机翼扣重平衡,作动器、载荷传感器、杠杆扣重等。试验载荷按要求以5%一级,根据随动加载载荷函数,逐级加载至100%载荷。机翼的扣重采用 “三点式”分布,即将左右机翼重心重量分别分布至三点,共六点进行联合扣重。作动器、载荷传感器、杠杆等加载设备的扣重采用随动扣重,即加载设备的称重量通过每级载荷方向与竖直方向夹角β(机翼弯曲变形偏转角度)的几何关系求得。

图11 试验井架安装
4.2 试验组成及情况
试验系统分为五大系统,包括随动系统、支持系统、控制系统、采集系统、油压系统等。随动加载系统组成为翼面帆布袋、多级杠杆系统、力传感器、加载作动筒、移动滚轮、随动作动筒、随动作动筒固定座等结构。该试验以100%限制载荷为试验载荷,具体加载为按5%限制载荷为一级分20次逐级加载至100%限制载荷,而随动加载系统在随动作动筒控制下根据每一级翼尖变形量计算出的滑动量实时调节加载系统的载荷位置和加载方向,使加载方向始终垂直与翼面,从而实现机翼载荷的随动加载,加载与卸载均逐级测量。
试验加载过程平稳,双作动筒跟随性良好,未出现超差、报警、卡滞现象等,机翼弯曲变形情况正常,无异常响声。限制载荷试验卸载后,试验件无可视永久变形。
4.3 试验数据分析
该试验主要目的在于考核该随动加载系统加载过程是否可行、可靠;机翼上下壁板应变变化是否平稳;机翼翼尖变形是否正常;左右机翼变形是否对称等问题,所以数据分析重点集中在机翼壁板应变数值的线性度,机翼变形对称性及机翼变形随加载级数增加是否平稳,以及机翼变形与理论分析的吻合性。
为了分析机翼壁板应变线性度,选取机翼任意部分位置应变数据进行分析(如图12所示)。机翼向上弯曲变形,所以上壁板压缩变形,应变为负;下壁板拉伸变形,应变为正。
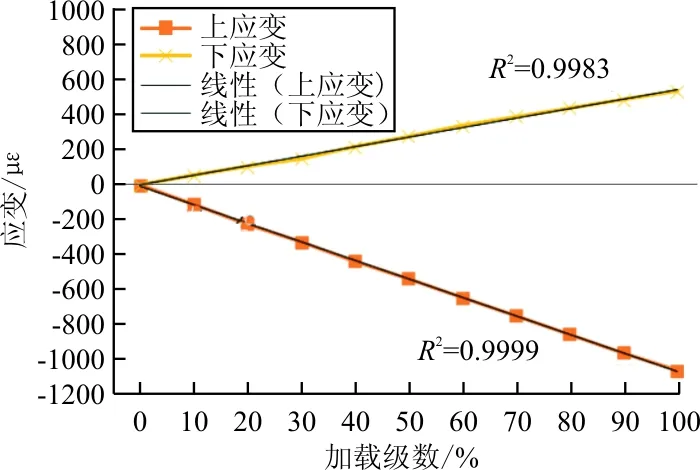
图12 应变数据线性度
图12中分别为机翼上、下蒙皮应变,该结果与试验前期估计一致。根据应变的线性度R2值为0.998和0.999,所以测试点应变位测试数据线性相关系数优于0.9,线性度良好,试验过程中应变数据变化平稳。
为了分析机翼变形对称性,对左右机翼选取任意对称位置的位移测试数据进行对称性分析,并给出对称曲线,如图13所示,其中左侧1代表左机翼外段位移数值,左侧2代表左机翼内段位移数值,右侧1代表右机翼外段位移数值,右侧2代表右机翼内段位移数值。可以看出:左右最大差值Δmax=3 mm,左右机翼对称测试点位移数据对称性良好。

图13 位移数据对称性
为了分析机翼翼尖随加载级数增加的变形情况,在加载过程中,从10%~100%逐级选取测量数据,将左右机翼翼尖处位移测试数据与理论计算数据进行对比,如图14所示,可以看出:Δmax=15 mm,与理论计算最大变形量1 250 mm相比,差1.2%,该试验位移曲线与理论位移曲线重合度高,试验结果理想。

图14 翼尖位移与理论位移对比
为了验证飞行载荷情况下,机翼各肋变形量与展向站位的关系符合二次曲线规律,从而验证理论分析结果的正确性,选取左侧机翼实测变形位移量与理论曲线进行对比,如图15所示,可以看出:机翼实测变形与理论计算吻合度高,数据变形趋势一致,误差小,试验数据理想。

图15 满载情况机翼变形量与展向站位关系
5 结 论
(1) 本文对大展弦比机翼试验随动加载系统进行开发和试验应用,该随动加载系统实现了载荷方向与翼面弦平面的动态垂直,试验加载过程平稳,双作动筒跟随性良好,未出现超差、报警、卡滞等现象,机翼变形均匀、无抖动,应变曲线符合要求。该随动加载系统的应用可以为类似随动加载系统提供设计依据,具有较大的现实意义和应用价值。
(2) 通过翼尖变形试验实测数据与理论研究进行对比,实测数据和理论数据对比曲线吻合度高,数据变形趋势一致,翼尖处位移误差小。试验结果证明了模拟分析计算的准确性,同时验证了该试验方案的合理性,可以为类似飞机机翼设计提供参考意义。

