基于拓扑密度云图的铝合金轮毂减重分析

单 萍，郑忠才，李 飞，李 达

（山东建筑大学，济南 250101）

0 引言

2016年，我国颁布的《节能与新能源汽车技术路线图》指出，到2020年，乘用车新车平均油耗要求达到 5.0L/100km；到2025年，乘用车新车平均油耗达到4.0 L/100km；到2030年，乘用车新车平均油耗达到3.2 L/100km[2]。而欧洲铝协研究数据表明：汽车质量每降低100kg，每百公里可节约0.6L燃油[3]并且每千克铝合金的使用可以减少13～20kg温室气体的排放[4]，针对如今日益严格的排放法规与日益恶劣的环境问题，实现整车轻量化势在必行。

在一台完整的车上，有着许许多多的零部件，而轮毂是汽车上必不可少的零件之一，它承受的不止仅仅是静态时车辆本身的自重，而且在车辆运行中需要承受交变载荷，同时在启动、制动、加速、减速过程中，车轮需承受扭转力矩[5]，在众多材料的轮毂中，铝合金轮毂因为其自身所特有的优势：质量轻、散热性好等优点[6]，一直被人们所关注。本文针对铝制轮毂进行了拓扑优化设计，以达到轻量化目的，并以此结果为基础，对其在三维软件中进行修改建模。同时为了保障优化后的强度问题，在优化修改后再一次进行了弯曲疲劳测试，并观察其最大应力和最大位移的变化情况。

1 铝合金轮毂建模

1.1 铝合金轮毂三维实体造型

本文以较为常用的14×5.5J铝合金轮毂做为优化对象，本次优化采用的三维实体建模软件为Solidworks软件，为了在后续的分析中缩短计算时间与储存空间，在此选择对螺栓进行简化处理，其三维实体造型如图1所示。

图1 轮毂三维实体模型

1.2 铝合金轮毂有限元实体模型

依据已知实体尺寸，在SolidWorks中建立实体模型，并将其保存成有限元可读取的x_t格式，之后将其导入进有限元软件中，进行后续分析。由于主要研究对象为轮毂，为了减少运算时间，决定对轮毂和加载轴实现不同的网格划分，并在连接处进行细化处理，对轮毂选用网格尺寸7mm的四面体单元，对加载轴选用自由网格进行划分，共计总的节点个数为153486个，总单元数为94008个，本次所划的85%网格单元质量都在0.5以上，网格质量情况良好，具备进行后续优化设计的前提。划分网格之后的模型如图2所示。

图2 轮毂有限元模型

1.3 铝合金轮毂材料参数

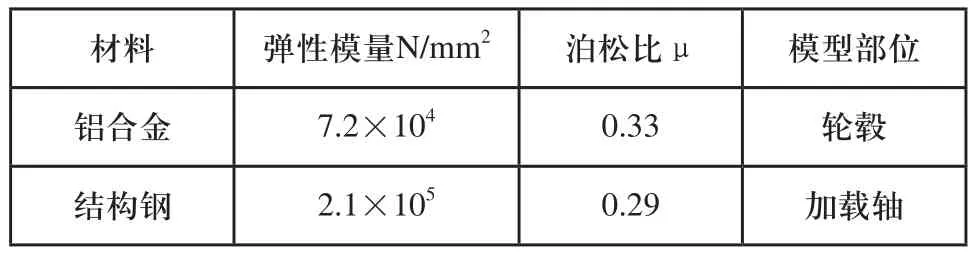
表1 14×5.5J铝合金轮毂材料参数

2 弯曲疲劳试验

2.1 弯曲疲劳试验工况分析

在进行弯曲疲劳实验时，车轮可自由选择测试工况，其一为车轮需要在固定不变的弯矩下进行旋转，其二为车轮需保持静止不动，其本身需要承受一个旋转弯曲力矩[7,8]，具体实验装置为图3。

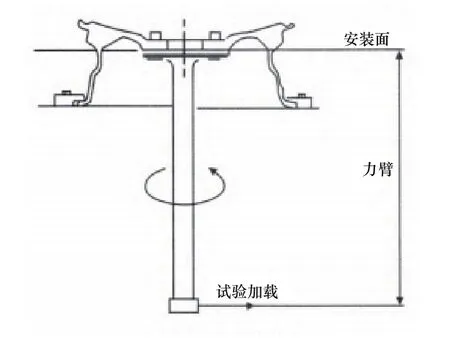
图3 弯曲疲劳实验装置

2.2 载荷计算及约束条件

1）载荷计算

在载荷分析时，选择以弯曲疲劳试验为模拟依据，因为其可以较好地反应出轮毂在实际工况中的受力情况。试验弯矩估算依据为公式(1)：

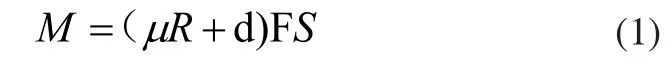
上面式(1)中：

M为加载的弯矩；

μ为轮胎与路面之间的摩擦系数设为0.7；

R为静载半径；

d为车轮的内偏距或外偏距，取绝对值；

F为车轮的最大额定载荷设定为1.6；

S为实验强化系数。

结合该车轮的实际参数，计算出所需加载弯矩为2613.3N.m，根据式(2)计算出需施加在加载轴上的力。

本次试验中选取的加载轴的长度为0.5m,据此计算出F为5226.6N，为了模拟轮毂在实际中的应用工况，将F分解为X方向与Y方向，使FX按照正弦规律变换，使Fy按照余弦规律进行变换，并同时进行加载，保证了合力的大小不发生变化，只变化方向从而可以实现加载旋转载荷模拟实际工况。

其中t为时间。其变化规律可绘制如图3所示。

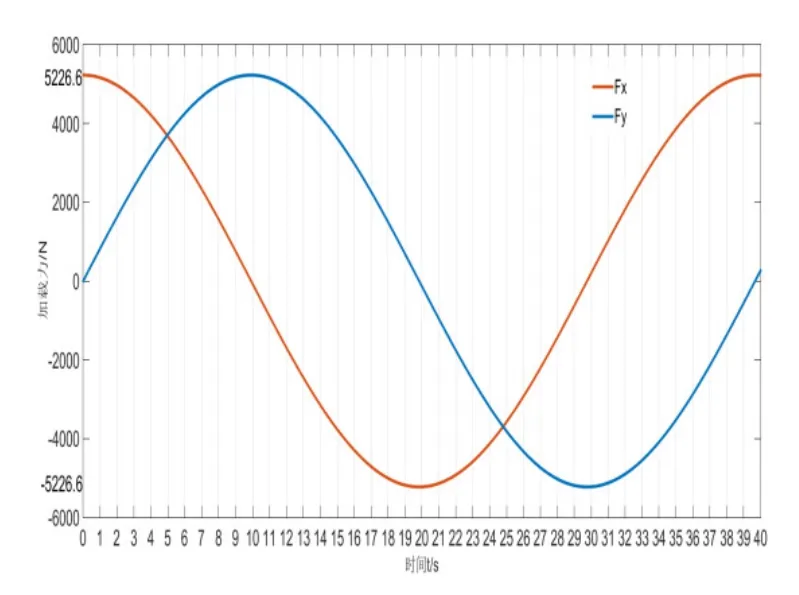
图4 弯曲疲劳模拟所施加载荷

本文将所施加载荷进行360度连续旋转离散为在40个方向上进行分别的加载，即使力实现间隔9度进行多次加载，共实现加载40次，将式(3)中的t分别取整数为1至40，由于本次主要完成的为静力学分析，所以无须考虑惯性力的影响。

2）约束条件

在分析时为了简化，忽略了螺栓及其预紧力，并定义了加载轴与轮毂之间的接触面，根据《GBT5334-2005乘用车车轮性能要求和试验方法》：在进行弯曲疲劳试验中车轮需要被固定在实验台上，以模拟车轮在行驶过程中的实际工况[9,10]，所以在模拟疲劳试验时，约束条件为对轮毂的下边缘6个自由度进行全约束设置。

3 铝合金轮毂有限元模拟分析结果

车轮处于旋转弯曲载荷工作状态时，其所呈现的是非常复杂的应力状态，在充分研究各轴的综合应力的情况下，选择采用形状改变比能理论，即以Von Mises屈服准则作为此次分析的依据，发现应力在空间分布上显示为呈中心对称趋势；在时间上，呈现出周期性变化具体如图4所示。由于呈现周期性变化，在此我们仅研究半个加载周期[11]，可以看出应力的最大值出现在第10载荷步，其大小为156Mpa。

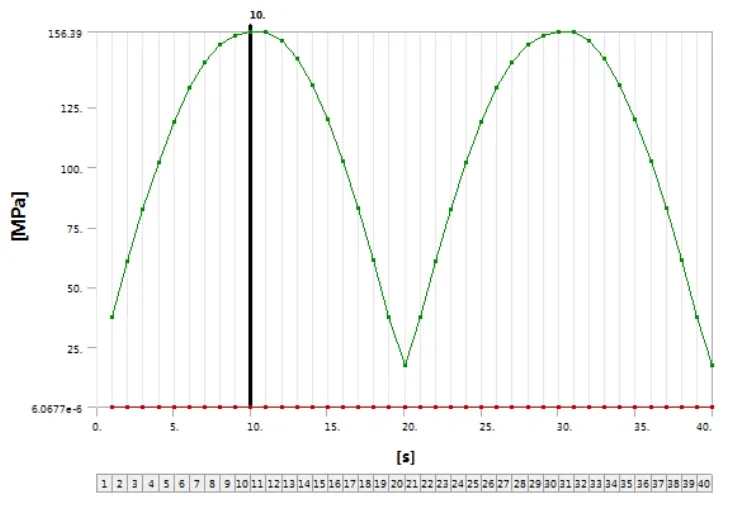
图5 应力变化情况

基于此，为了保证安全性，选取最大应力值载荷步进行分析，提取该载荷步下的等效应力云图5和等效位移云图6进行观察。

图6 轮毂结构等效应力云图

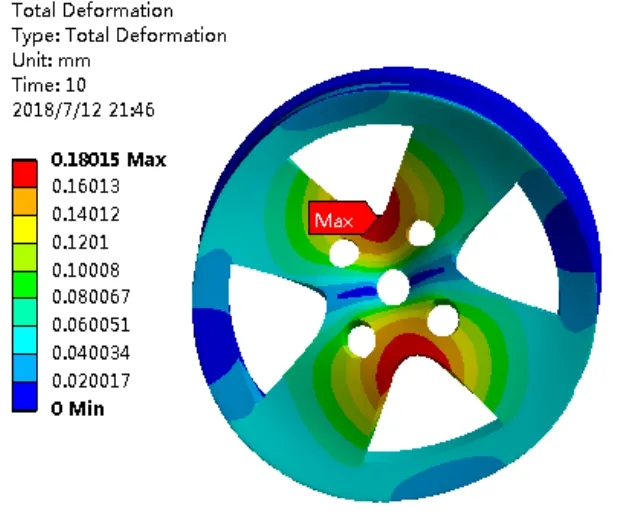
图7 轮毂结构等效位移云图

可从上图看出最危险的地方在节点1579处即螺栓与加载轴连接处附近，符合实际应用中的工况，在此处应力值达到156MPa，但是仍然远远小于材料强度极限，其变形量为0.18015mm，其强度与变形量仍有较大改进空间，具有轻量化的前提条件。

4 轮毂轻量化设计

4.1 拓扑优化设计

拓扑优化设计主要用于现有设计中的重量缩减部分，其优化流程为：建模、划分网格、定义载荷及约束，设置重量优化目标，最后进行求解。本次的减重目标设定为原始结构的50%，在进行优化设计后，可以看出模型显示出不同的颜色，其中红色部分是建议删减部分，从得到的图7拓扑优化图中可以看出毂边缘部分可以进行着重进行减重设计，基于拓扑优化给出的减重范围，将模型的轮毂厚度由初始的15.55mm缩减至12.92mm，在原轮毂其他结构不发生变化的前提下，在SolidWorks中进行三维模型的修改。

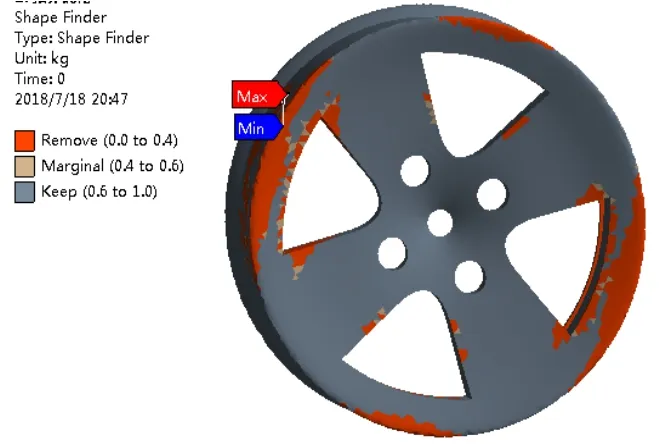
图8 拓扑密度云图

4.2 强度校核

优化设计之后轮毂质量由有原来的8.7087kg减少至6.8169kg，重量缩减21.72%，但是是否满足强度要求仍需进行理论分析，将修改后的模型重新导入有限元中，在与未优化之前的约束与加载条件完全相同的情况下，再次进行弯曲疲劳试验，进行求解，得到图8改进后轮毂结构等效应力云与图9改进后轮毂结构等效位移云图。

图9 改进后轮毂结构等效应力云图

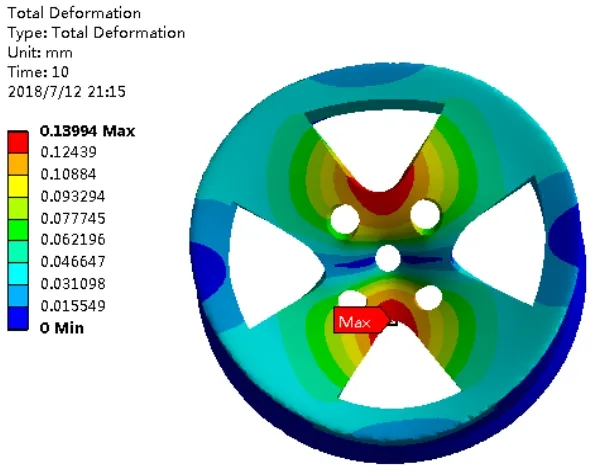
图10 改进后轮毂等效位移云图

由图8、图9中可以分析出，在该轮毂强度方面最大等效应力为144MPa对比未改进之前的最大等效应力156MPa，降低了7%，最大等效位移0.13994mm对比未改进之前的最大等效位移0.18015mm，变形程度有了显著地减轻。最大应力与最大变形所在位置仍然处于螺栓与加载轴连接处附近，符合实际中应用工况。该次减重优化设计无论从从静态结构分析还是轻量化方面，都达到了预期的设计目标。

5 结论

本文针对对规格为14×5.5J的铝合金轮毂进行轻量化设计，整体实现减重21.72%。

进行数次优化之后，最大应力点与最大变形位置仍出现在螺栓与加载轴连接处附近，在进行实际设计时，需对此处危险点进行材料或者结构的强化，以使轮毂更为安全可靠。