发电机励磁与STATCOM模糊滑模非线性协调控制方法的研究

李鹏飞，孙崧强，张 蕾，宋博雄，景军锋

（西安工程大学 电子信息学院，西安 710048）

0 引言

随着互联大电网的发展，电力能源互联成为电网发展的必然趋势[1]，并因此带来了系统运行越来越复杂，系统维度不断提高，电力系统的容量越来越接近极限等问题，使电网稳定性问题日益突出[2]。而静止同步补偿器（STATCOM)作为柔性交流输电系统（FACTS）[3]中的重要设备，具有调节范围宽、体积小、可实时的补偿系统的无功功率等优点[4,5]，并且在降低损耗、稳定电压、降低谐波、提高系统暂态稳定性等多方面具有优越性能[6～8]，通过其参数的柔性控制可有效地提高电力系统的传输容量并增加电力系统的静态和暂态稳定性，因此得到了广泛的关注和大量的研究[9～11]。

发电机励磁是解决稳定性问题的传统方案和新控制方法的试金石，研究表明，通过在系统中装设STATCOM并通过协调控制可以进一步发挥励磁和FACTS装置对稳定性的作用[12]。因此，国内外学者在STATCOM与发电机励磁协调控制方面进行了大量研究。

文献[13]联合直接反馈线性法（DFL）和零动态设计原理，针对发电机励磁和STATCOM电流源模型进行协调控制研究，存在问题是被控对象电流型STATCOM数学模型过于理想化，在参数发生摄动时其控制效果难以保证；文献[14]在DFL的基础上结合鲁棒控制方法，对被控系统进行线性化处理，保证了功角稳定和电压调节，但仍需要依靠动态扩展消除被控系统的稳态误差；文献[15]针对STATCOM和励磁控制系统的数学模型设计了基于DFL和以T-S模型为基础的模糊滑模控制理论的非线性控制律，虽然所设计的控制律可以保证发电机功角和STATCOM接入点电压的稳定，但是其对于发电机端电压扰动的鲁棒性不强。综上所述，学者们在非线性控制器方面已经做了大量的研究和探索，很多非线性控制方法在维持系统稳定方面取得了良好的效果，但是很多研究在本质上都没有摆脱基于被控对象模型的确定性思想，需要给定精确模型，这限制了非线性控制方法在控制性能上的提升。

而装设STATCOM的输电系统中，系统的阻尼系数、机械功率等参数由于工作情况的改变而存在参数不确定性，同时系统在运行过程中易遭受故障而使系统遭受不确定扰动。基于变结构控制方法的滑模变结构控制算法具有与被控对象的参数与扰动无关的特性，因此，本文采用滑模变结构控制算法来设计发电机励磁与STATCOM非线性协调控制的控制方法，并针对滑模变结构控制方法所固有的抖振问题，设计了一个一维的模糊控制器，根据当前状态变量距离滑模面的距离，实时地调整控制律的参数，从而加快了收敛速度，并且能有效地减少系统的抖振问题，最后通过仿真验证了所设计的模糊滑模协调控制器（FSMCC）在提升系统稳定性品质方面具有很大优势。

1 系统模型及控制目标

本文考虑如图1所示的含有STATCOM的单机无穷大系统（SMIB），带有励磁设备的发电机经过变压器与双回路供电的输电线路相连，STATCOM装设在输电线路的中点处，这也是最能发挥STATCOM对电压稳定性的接入点[16]。

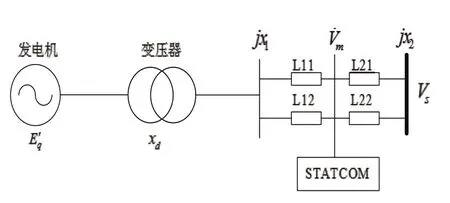
图1 含STATCOM的SMIB系统

在不考虑线路有功损耗和STATCOM的内部结构的前提下，采用带有励磁设备的发电机的三阶非线性微分方程和STATCOM一阶可控电流源模型，则包含STATCOM的SMIB系统非线性状态方程可表示为[17]：

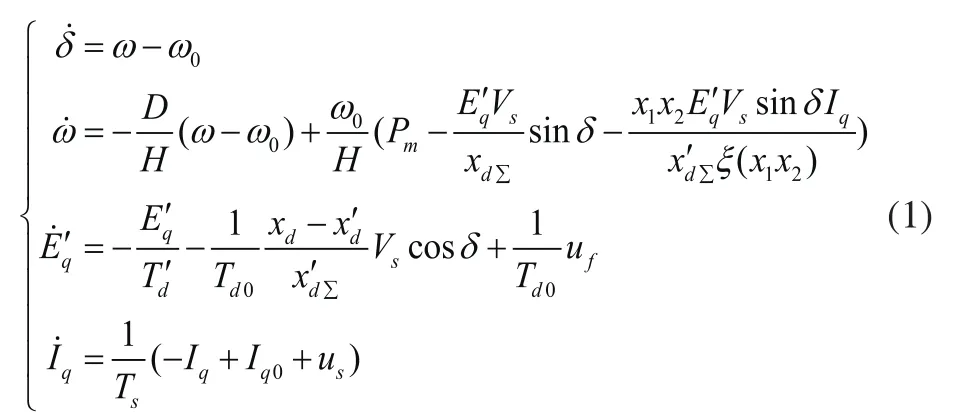
式中：δ是发电机功角；ω是发电机角速度，ω0是发电机的额定同步角速度；是发电机q轴暂态电势；Vs是无穷大系统母线电压，设为1（标幺值）；Iq是STATCOM所等效的可控电源输出电流；D是发电机阻尼系数；H是发电机转子的转动惯量；Td0是d轴绕组开路暂态时间常数；是d轴绕组短路暂态时间常数；Pm是原动机机械功率；xd是发电机d轴同步电抗；是发电机d轴暂态电抗；Ts是STATCOM的惯性时间常数；uf、us分别为励磁设备的控制输入和STATCOM的控制输入。；其中为变压器阻抗；，xL22为线路阻抗；Pe为发电机输出的电磁有功功率。其表达式为：

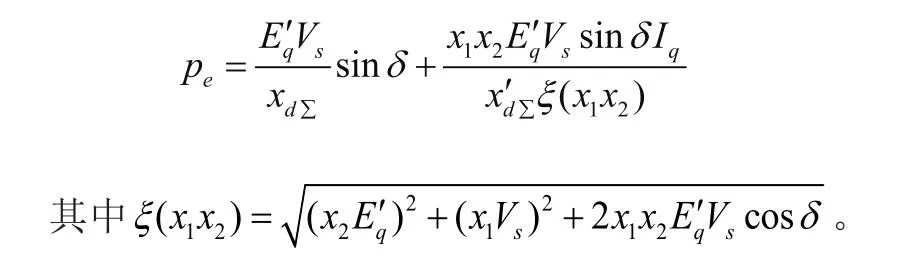
控制器设计的目标是当系统在运行中遭受不确定扰动时，发电机励磁与STATCOM协调控制器能够迅速迫使系统恢复稳定,并且在过渡过程中保证接入点电压不会出现大幅跌落，发电机功角不会失去同步。根据这一控制目标，本研究将发电机的功角增量δ-δ0和STATCOM接入点的电压增量Vm-Vref作为控制系统的调节输出：

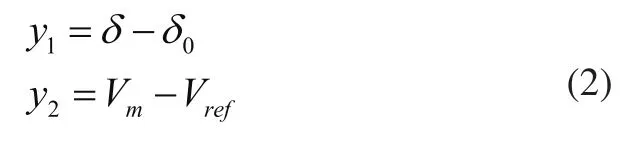
式中：Vm为STATCOM接入点电压，，Vref为参考电压。

2 发电机励磁与STATCOM模糊滑模协调控制器（FSMCC）的设计

滑模变结构控制具有不受参数变化的影响，鲁棒性强，动态性能好等优点，但是在系统临近稳态时，不可避免的会出现抖振问题。本文采用一维模糊控制器来动态调整控制参数，在加快系统状态收敛的同时可有效地抑制抖振，并且因为引入了模糊逻辑推理机制，使STATCOM控制器在复杂、不确定的非线性电力系统控制环境中具有更好的控制效果和更高的鲁棒性能[18]。

2.1 无穷大系统模型的精确线性化

在采用滑模变结构控制设计协调控制器之前，首先将系统(1)变换成标准形式的仿射非线性系统，如式(3)所示。

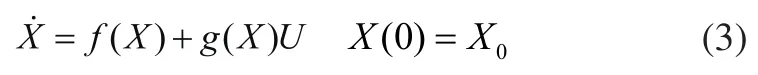
式中：

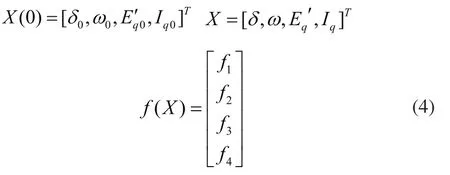
其中：

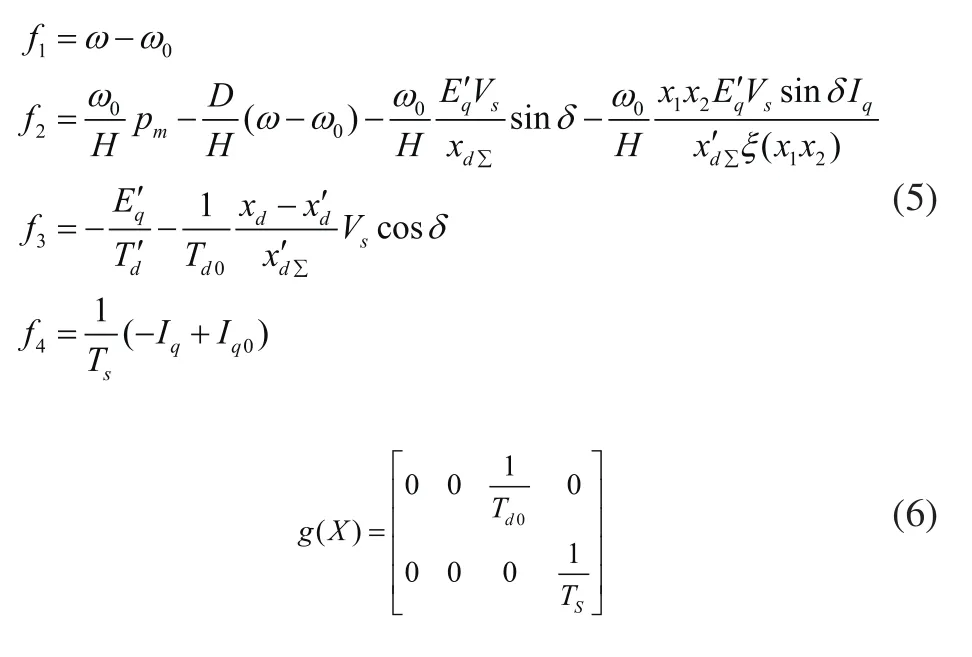
然后，对仿射非线性系统(3)，求其对系统调节输出y1(X)，y2(X)的各阶李导数：

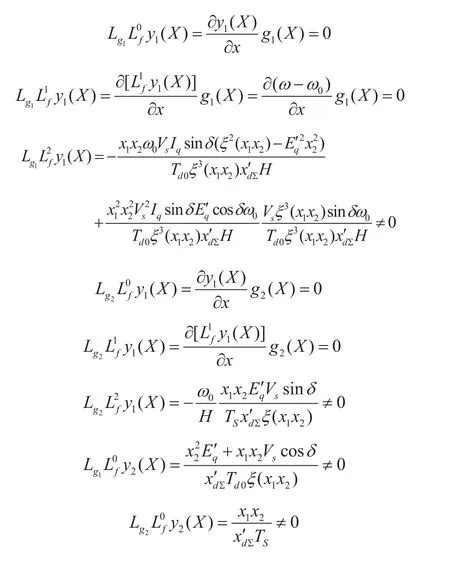
由上述相对阶的计算可知：对于控制系统输出y1=δ-δ0和y2=Vm-Vref的关系度分别为r1=3和r2=1；所以该控制系统的关系度集合为r=r1+r2=4=n，也就是说等于系统的阶数，因此精确线性化问题有解。

令：

根据多输入、多输出精确线性化理论以及映射坐标选择原理，可以得到变换后的坐标为：

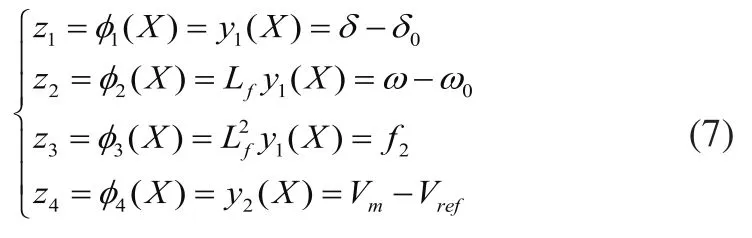
因此，将原状态方程转化为一个完全可控的系统。通过坐标变换7），可将系统3）转化为以下Brunovsky标准型形式：

系统的输出方程为：

其中：

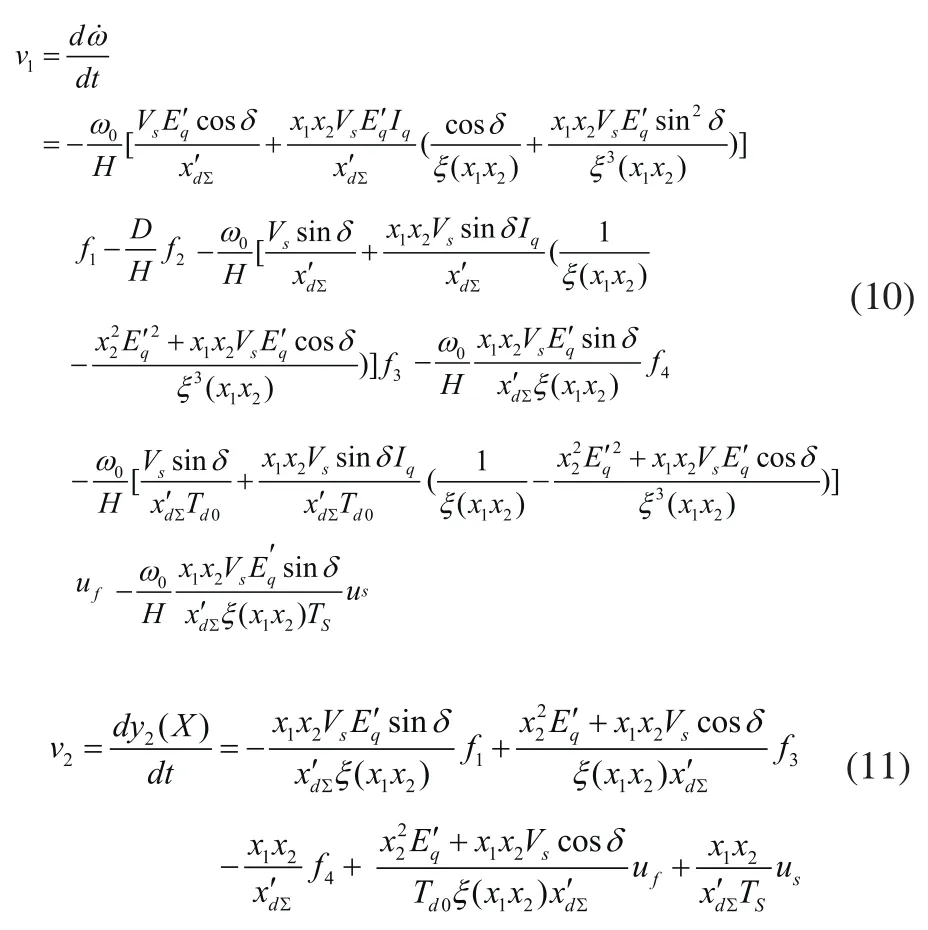
令：

可得到其状态方程：

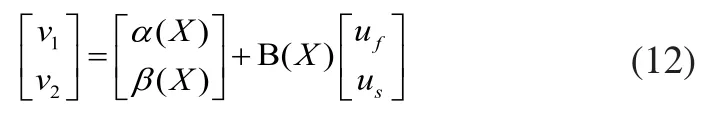
将式(12)进行变换，最后得到输入：

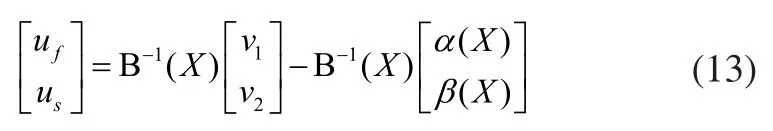
式(13)也可写成变换后形式：

（2）逻辑层：系统核心功能的实现层。根据应用层为用户提供的六大功能界面，逻辑层需要分别给出对应模块的实现方法。其中，基于传输控制协议（TCP）的Socket多线程并发模块是整个逻辑层能够顺利运行的框架基础，系统利用该模块实现多节点之间数据的可靠传输。进一步地，运用里所码的编码解码方式对电子数据进行分片处理，引入用户节点性能测试模块，对节点性能进行排序，用于数据的上传和下载功能模块；引入Hash比对模块检测文件数据是否保存完整；引入用户积分模块，保障系统的负载均衡；引入用户注册、登录功能记录用户信息，方便对用户进行管理。

其中：

对系统进行精确线性化处理之后，然后根据系统控制目标进行滑模面的设计。

2.2 基于模糊滑模算法的FSMCC设计

首先，根据系统控制目标需要实现发电机功角稳定，取第一个滑模面为：

根据式(8)、式(9)得：

为了实现控制目标中的电压稳定，取第二个滑模面为：

对其两边进行求导，可得：

对于前述两个控制目标，本文采用指数控制律来设计状态变量到达切换面的趋近特性，则：

具体控制规则描述为：将输入变量|S|和输出变ε进行非均匀离散为零（ZR）、正小（PS）、正中（PM）、正大（PB）4个等级，并在接近滑模面S=0时进行细分，远离滑模面S=0时进行粗分[20]。

采用Mamdani推理方法[21]实现上述控制规则，采用重心法[22]解模糊，清晰化控制量ε0为：

式中：bi为输出论域中的一个点；表示bi点的隶属度。ε0确定后经过比例变换可获得实际控制量ε。

由式(17)、式(20)、式(21)可得：

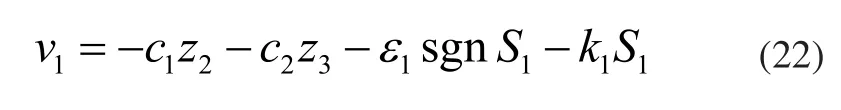
为了达到STATCOM接入点电压稳定的目的，取S2=0，结合式(19)、式(20)、式(21)可得：

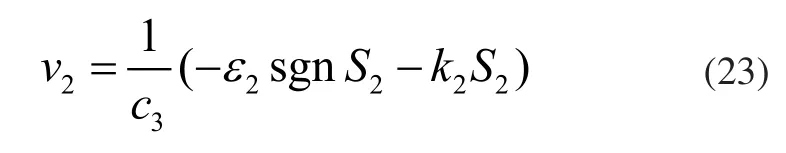
将式(22)和式(23)代入式(13)得到最终的FSMCC协调控制律为：

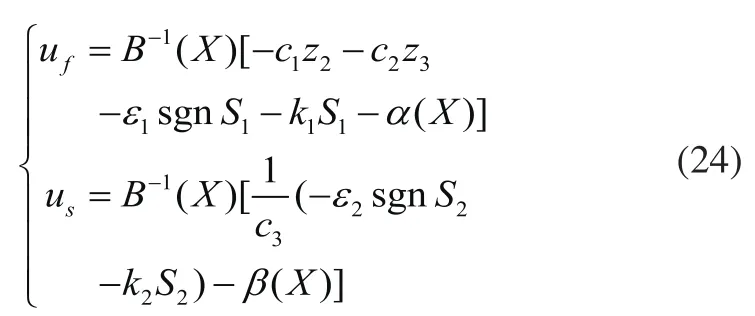
3 仿真验证

为了验证所设计的FSMCC对发电机功角和接入点电压在系统参数不确定和遭受不确定扰动情况下的控制效果，针对图1所示的含有STATCOM的SMIB系统进行仿真。选取参数如下：H=8，D=1.0，xd=0.8，x'd=0.3，Td0=6.9，Pmo=0.8，xT=0.15，xL11=xL12=0.4，xL21=xL22=0.6，ω0=314.6，δ0=60o，Vref=1.0，Vs=1.05，Ts=0.02，Iq0=0.75，-1.5≤Iq≤1.5。

并在三相短路故障情况下，将所设计的FSMCC算法分别与发电机励磁采用的最优控制+STATCOM采用比例积分控制（LOC+PI）和发电机采用最优控制+STATCOM采用变结构控制（LOC+VSC）的分开控制方法进行暂态仿真的对比。

情况1：对系统在三相短路故障情况下进行仿真。故障设置为：在1s时线路L11处发生三相短路故障，0.1s后切除线路故障，由L12单独供电，并且在1.5s时故障消除，恢复双回路供电。发电机功角和STATCOM接入点电压的暂态响应曲线如图2(a)和图2(b)所示。

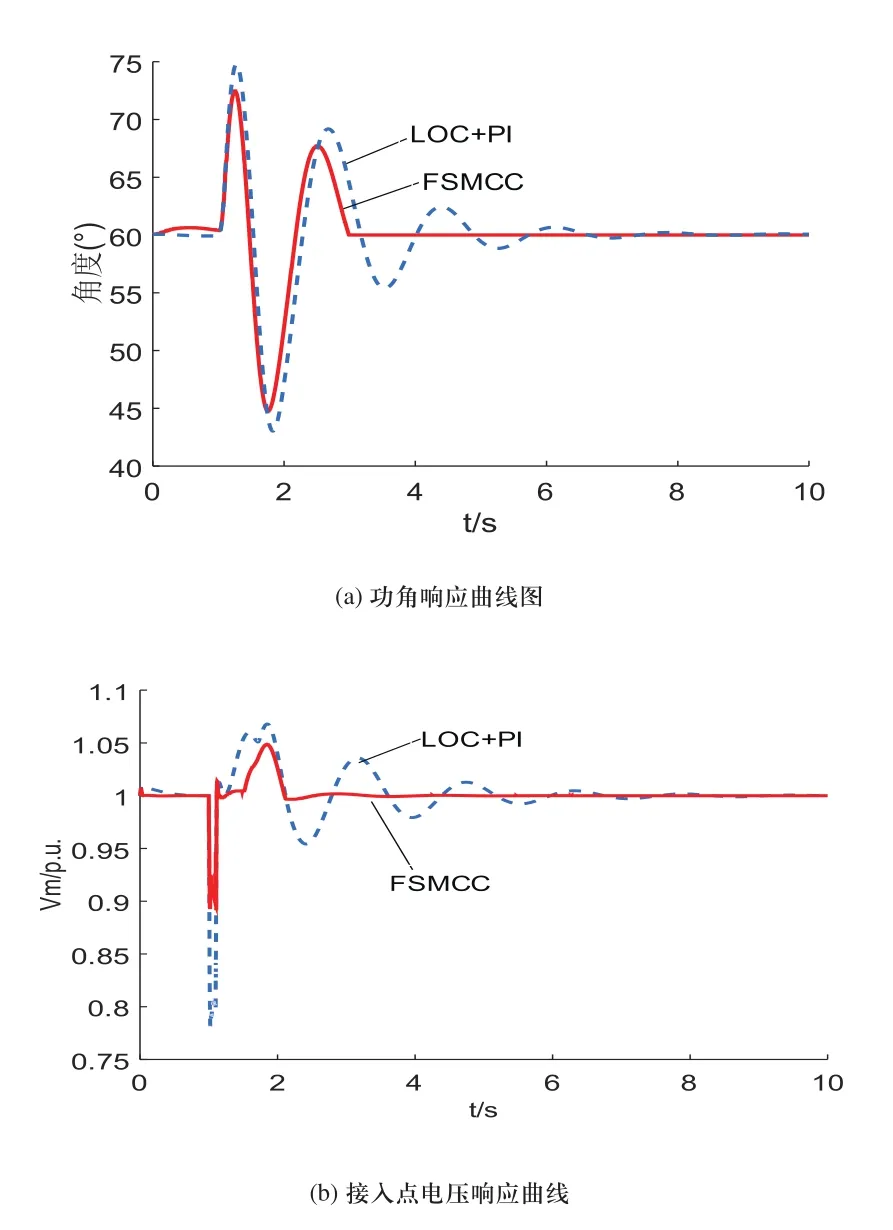
图2 工作情况1下变量响应曲线

图2(a)表示两种控制策略的发电机功角响应曲线，实线表示本文所设计的FSMCC在大扰动作用下的响应曲线图，虚线表示LOC+PI分开控制策略在相同情况下的响应曲线图。从图中可以看出，在所设计的FSMCC作用下相对于LOC+PI分开控制的效果更好，发电机功角在3s左右基本达到新的稳定状态，功角振幅超调量小于LOC+PI控制策略。图2(b)表示STATCOM接入点电压响应曲线图，当系统发生故障的瞬间，电压迅速下降，由图可见系统接入STATCOM并采用所设计的FSMCC使电压跌落后迅速上升最低跌幅在0.9p.u左右,且在3s可迫使电压恢复新的平衡，而在传统的LOC+PI分开控制策略下，电压跌落在0.8p.u以下，可见通过所设计的FSMCC策略使STATCOM接入点电压得到了更有效的支撑，在大扰动情况下缩短了过渡过程，提高了系统的暂态稳定性能，对扰动具有较好的鲁棒性。

情况2：为了更进一步验证所设计FSMCC对电力系统稳定性的作用，设计了发电机励磁最优控制加利用饱和函数来抑制抖振的STATCOM变结构控制策略下的控制器（LOC+VSC），并把本文所设计的FSMCC与其在同样的扰动情况下进行暂态仿真对比。故障设置为：在1s时线路L11处发生三相短路故障，0.1s后切除线路故障，由线路L12单独供电，并且在1.5s时故障消除，恢复双回路供电。发电机功角和STATCOM接入点电压的暂态响应曲线如图3(a)和图3(b)所示。

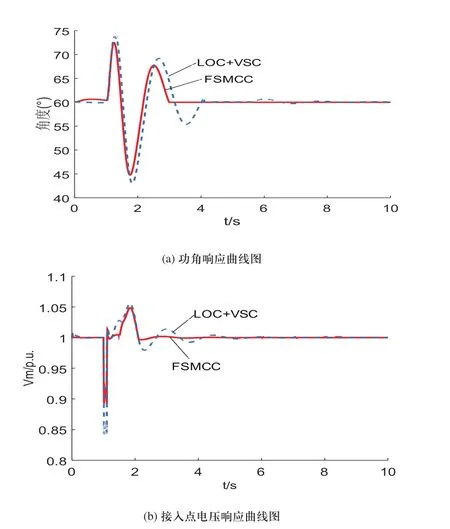
图3 工作情况2的变量响应曲线

图3(a)表示两种控制策略下的发电机功角响应曲线，实线表示本文所设计的FSMCC在大扰动作用下的响应曲线图，虚线表示LOC+VSC分开控制策略在相同情况下的响应曲线图。从图中可以看出，所设计的FSMCC相对于LOC+VSC分开控制的效果更好，LOC+VSC在4s左右达到稳定，而FSMCC使发电机功角在3s左右达到新的稳定状态，功角振幅超调量小于LOC+VSC控制策略，并且整个过程没有出现明显的抖振现象。图3(b)表示STATCOM接入点电压响应曲线图，当系统发生故障的瞬间，电压迅速下降，由图可见系统接入STATCOM并采用所设计的FSMCC使电压跌落后迅速上升最低跌幅在0.9p.u左右，且在3s可迫使电压恢复新的平衡，而在LOC+VSC分开控制策略下，电压跌落在0.85p.u以下，可见通过所设计的FSMCC策略使STATCOM接入点电压得到了更有效的支撑，在大扰动情况下缩短了过渡过程，提高了系统的暂态稳定性能，对扰动具有较好的鲁棒性。

4 结束语

本文采用滑模变结构控制方法和模糊控制方法相结合，设计了一种发电机励磁-STATCOM模糊滑模非线性协调控制方法，该算法通过设计一个一维模糊控制器克服了传统滑模变结构控制存在的抖振问题，通过设计可调参数来控制状态变量达到滑模面的动态特性。通过与采用发电机励磁和STATCOM分开控制的算法在系统遭受故障的情况下分别做了仿真对比，仿真表明：所设计的FSMCC能同时改善系统功角特性和接入点电压特性，并且抑制了由滑模变结构所带来的抖振问题，不管是从系统性能还是响应时间上，FSMCC控制器在提高系统稳定方面有较高品质。