函数中的三 类易错题
胡 珏
有些同学在做函数问题时,感觉做对了,结果却又做错了。这主要是由于同学们对概念、性质理解不透导致的。为了帮助同学们更好地掌握这部分内容,下面以例题的形式总结了函数问题中的3类易错题。
一、概念问题
例1 已知函数y=(m-1)y||m+5m是一次函数,则m的值为( )。
A.1 B.-1 C.0或-1 D.1或-1
【错解】D。
【错因】忽略一次函数定义中的隐含条件。
【正解】B。
【点评】本题根据一次函数的概念求m的取值范围时,要考虑两个方面,一是函数的指数为1,二是该函数的一次项不能为0。同学们很容易忽略第二点。
二、性质运用问题
1.反比例函数中的几何意义。
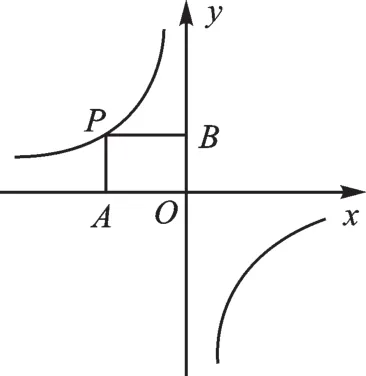
【错因】错解知道k的几何意义,但忽略了图像的性质。当k<0时,图像在第二、四象限。
【点评】本题考查的是k的几何意义,同学们容易忽视k的值还与图像的位置有关。
2.二次函数中的平移。
例3 若抛物线y=x2-2x+3不动,将平面直角坐标系先沿水平方向向右平移1个单位长度,再沿竖直方向向上平移3个单位长度,则原抛物线的表达式应变为_______。
【错解】y=(x-2)2+5。
【错因】错解误将平移平面直角坐标系看作平移抛物线。
【正解】y=x2-1。
【点评】抛物线的平移规律为“左加右减,上加下减”,这个规律的适用范围是坐标系不动,抛物线平移。本题是抛物线不动,坐标系平移,所以平移规律与上述规律正好相反。
3.函数图像。
例4 在同一平面直角坐标系中,函数y=ax+b与y=bx2+ax的图像可能是( )。
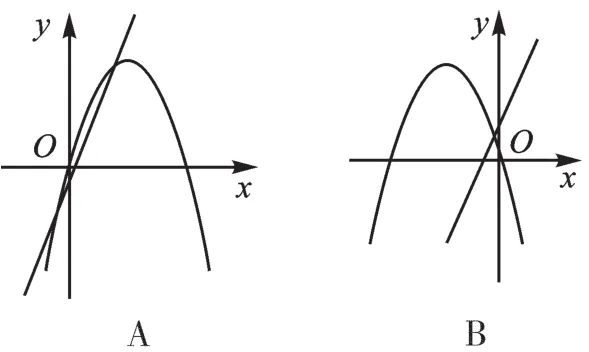
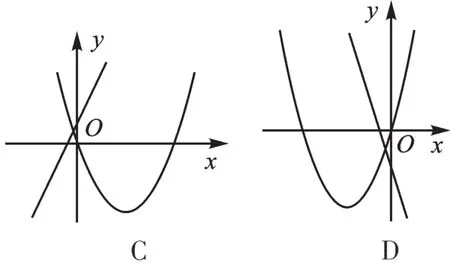
【错解】B、C或D。
【错因】遗忘一次函数的图像性质,难以根据一次函数图像信息判断a、b分别与0的大小关系;或者不清楚二次函数的图像性质,判断出了抛物线开口方向,却忽略了顶点位置。
【正解】若a>0,b>0,则y=ax+b经过第一、二、三象限,y=bx2+ax开口向上,顶点在y轴左侧,故B、C错误;若a<0,b<0,则y=ax+b经过第二、三、四象限,y=bx2+ax开口向下,顶点在y轴左侧,故D错误;若a>0,b<0,则y=ax+b经过第一、三、四象限,y=bx2+ax开口向下,顶点在y轴右侧,故A正确。
【点评】本题考查二次函数与一次函数的图像,解题的关键是明确函数图像性质,利用分类思想解答。
三、分类问题
1.对“函数”概念的理解。
例5 如果函数y=mx2-6x+2的图像与x轴只有一个公共点,则m的值为_______。
【错解】∵y=mx2-6x+2的图像与x轴只有一个公共点,∴由b2-4ac=0,解得m=。
【错因】审题不清。题目条件是函数,该函数可以是一次函数,也可以是二次函数。所以要分类讨论:如果m=0,函数是一次函数,图像与x轴只有一个公共点,符合题意;如果m≠0,函数是二次函数,当b2-4ac=0时,顶点在x轴上,也符合只有一个公共点。
【点评】审题时要区分题目中的“函数”“二次函数”“一次函数”等概念性词语。
2.求函数表达式。
例6 已知一次函数y=kx+b中自变量x的取值范围是-4≤x≤2,相应的函数值的取值范围是-5≤y≤7。求此函数的表达式。
【错解】把x=-4,y=-5;x=2,y=7代入一次函数表达式中,可得{-4k+b=-5,解得{k=2,2k+b=7, b=3,则这个函数的表达式是y=2x+3。
【错因】x的取值范围与y取值范围的对应关系,并不是x与y的对应关系,所以应当有两种情况。
【正解】(1)当k>0时,y随x的增大而增大。x=-4时,y=-5;x=2时,y=7,同上解。(2)当k<0时,y随x的增大而减小。x=-4时,y=7;x=2时,y=-5。同理,由待定系数法可得函数表达式为y=-2x-1。综上所述,这个函数的表达式是y=2x+3或y=-2x-1。
【点评】本题主要考查一次函数的性质。当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小。注意要分情况讨论。
例7 若一次函数的图像y=kx+b与两坐标轴围成三角形的面积是8,且过点(0,2),求此一次函数的解析式。
【错解】设一次函数的图像与x轴、y轴分别交于A、B两点,则OB=2。∵直线与两坐标轴围成的三角形的面积是8,∴×OB×OA=8,
OA=8。∴点A的坐标为(8,0),由待定系数法可得此函数表达式为y=-x+2。
【错因】当OA=8时,忽视点A的坐标有两种可能:(8,0)或(-8,0)。
【点评】本题主要考查用待定系数法求一次函数表达式,要分情况讨论。

