电磁轨道炮U形电枢的水中阻力系数研究

向红军，王俊晓,2，张晓良，鲁 飞，肖 静

(1.陆军工程大学， 石家庄 050003； 2. 73146部队， 福建 泉州 362000;3.北京军事代表局， 北京 100000； 4.陆军第81集团军， 河北 张家口 075000)

电磁轨道炮由于其超高速、超远程打击的特点，可实现远程火力支援、临近空间攻防等，对现代战争具有战略性的意义，是当前各军事强国研究的重点[1-3]。目前电磁轨道炮仍存在很多瓶颈，其中发射过程中枢/轨之间的滑动电接触技术是制约其发展的一大技术难题[4]，而对此过程中的滑动电接触状态进行实时监控难度较大。目前主要是根据理论建立模型，预测滑动电接触过程以及对轨道和电枢界面的影响，并与发射后的接触界面形貌对比，反推滑动电接触过程。为此，必须对发射后的电枢进行无损回收。传统回收方式大多采用低密度固体回收介质，容易造成电枢表面的划伤，只能采用流体介质对电枢进行无损回收。电枢在流体介质中的阻力系数是回收装置设计的关键。目前电磁轨道炮大多采用U形电枢进行试验[5-8]，形状与传统的圆柱形弹丸差异较大。为此，本研究将通过理论分析、数值模拟分析及相关验证试验，得出U形电枢在水中的阻力系数，从而为电枢的无损回收方案设计提供理论支撑。

1 流体介质中弹丸运动的数学模型

根据流体中高速弹丸所受阻力理论，流体中弹丸受到的阻力与弹丸速度的平方成正比

(1)

式中：v是弹丸瞬时速度；t是时间；b为衰减系数，表征介质中弹丸速度衰减特性。

电枢在水中的特征衰减长度为式(1)中衰减系数b的倒数，用a表示，其物理意义为电枢速度衰减为初速度的0.368时，电枢在水中的行程，为此，a可以表示为

(2)

其中：ρ电枢为电枢密度；l为电枢有效长度；ρ水表示水的密度；CD为阻力系数。

由式(2)可知，在已知电枢密度ρ电枢和有效长度l、水介质的密度ρ水的情况下，只要能得到电枢的特征衰减长度，即可求得电枢在该密度介质中的阻力系数值。

2 基于流体的U形电枢回收仿真分析

利用有限元软件LS-DYNA构建U形电枢在流体介质中的仿真模型，通过数值仿真得到电枢在水中的特征衰减长度，从而得到U形电枢在水中的阻力系数。

2.1 仿真模型构建

2.1.1物理模型

仿真物理模型如图1所示，主要由电枢、空气、水3个部分组成。电枢宽度与高度为20 mm。根据 Chuang[9]的观点，电枢在入水过程中会产生冲击波，为了保证冲击波可以在流场中顺利传播，而不至于被边界反射回来影响流体的冲击区域，一般选取水域的宽度应为结构宽度的4～5倍。为此，空气域和回收介质域宽度和高度为100 mm，空气域的长度为60 mm，回收介质域的长度为1 000 mm。在模型单元算法设置中，电枢选用拉格朗日实体单元，采用*SECTION_SOLID中常应力实体单元算法；空气和水选用实体欧拉单元且采用*SECTION_SOLID_ALE关键字下，中心单点积分的ALE多物质单元算法。因此在实体建模过程中电枢和流体域部分可相互独立，而空气域和回收介质域的接触部分必须紧密连接，以保证网格划分时候二者可以共节点，确保物质可以在两个区域的网格内流动。建模完成后，对空气域和回收介质域四周施加无反射独立边界。

图1 物理模型

2.1.2材料模型

按照有限元仿真流程，需要对上述模型添加材料属性，其中电枢定义为铝合金材料，用关键字*MAT_PLASTIC_KINEMATIC定义，各项参数设置如表1所示。

表1 电枢材料参数设置

空气采用*MAT_NULL材料模型及*EOS_LINEAR_POLYNOMIAL状态方程加以描述[10]。根据LS-DYNA关键词手册，线性多项式方程表示单位初始体积内的线性关系和压力值P，即：

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

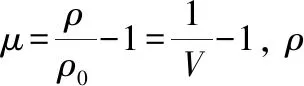
对空气而言，参数设置时C0=C1=C2=C3=C6=0，c4=c5=0.4。空气的密度取为1.29 kg/m3，初始相对体积V0取1.0。

回收介质采用*MAT_NULL材料模型及*EOS_GRUNEISEN状态方程表示，其中基于冲击波速度-粒子速度(vs-vp)的三次曲线Gruneisen状态方程，定义的压缩材料的压力为：

(γ0+aμ)E

式中：C为冲击波速度vs，即vs-vp曲线的截距(速度单位)，由于在数值上与声音在介质中的传播速度相同，有时也称其为声音在该介质中的传播速度；S1、S2、S3为vs-vp曲线斜率的系数；γ0是Gruneisen常数；a为常数，是对γ0的一阶体积修正；，V为相对体积。

回收介质各参数具体设置如表2所示。

表2 回收介质GRUNEISEN状态方程参数设置

2.1.3流固耦合设置

基于流体介质的电枢回收模型涉及固体电枢及流体域，故需进行流固耦合设置，流固耦合主要靠关键字*CONSTRAINED_LAGRANGE_IN_SOLID来实现，定义耦合类型为加速度和速度约束型，即完成流固耦合关键字的设置，实现了电枢与流体耦合时力的传递。在*CONTROL_ALE中，设置默认的介质数值方法为ALE方法，两次对流间的循环数为1，对流方法为二阶精度的Van Leer + Half Index Shift。

2.2 仿真结果分析

设定U形电枢的初速为200 m/s，利用上述仿真模型，对U形电枢在水中的速度衰减情况进行仿真计算，得到不同时刻、不同位置下的电枢速度曲线如图2所示。

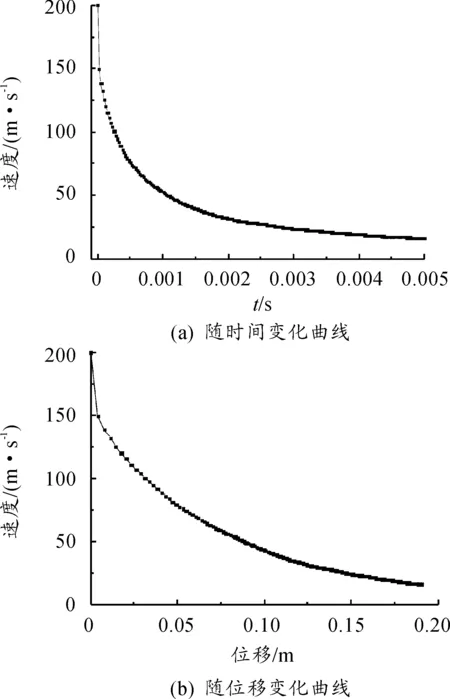
图2 U形电枢水中速度曲线

从特征衰减长度的定义可以，当U形电枢速度衰减为初速的0.368时，电枢运动的位移即为其特征衰减长度。

从图2可以看出，当U形电枢衰减为0.368时，电枢的运动位移为0.055 6 m。为此，U形电枢在水中的特征衰减长度为0.055 6 m。

3 U形电枢阻力系数计算

根据U形电枢在水中运动的数学模型，结合仿真计算得到的特征衰减长度，计算得到U形电枢的阻力系数。

3.1 U形电枢有效长度计算

从式(2)可知，要计算电枢在水中的阻力系数值，需要得到电枢密度、电枢有效长度及水介质的密度，在已知电枢及水的密度的情况下，对电枢有效长度进行计算。

电枢的有效长度是指电枢在前进方向上的实际长度。对于普通柱状弹丸而言，其有效长度即为弹体长度，可以直接进行测量；而电磁轨道炮所研究的电枢呈U形，其有效长度难以直接确定，需要通过计算进行界定。

本研究所选用的U形电枢的结构尺寸如图3所示，该电枢平面的面积为S，S的计算方法如下：

(3)

根据式(3)可得，电枢平面的面积约为333.472 mm2。

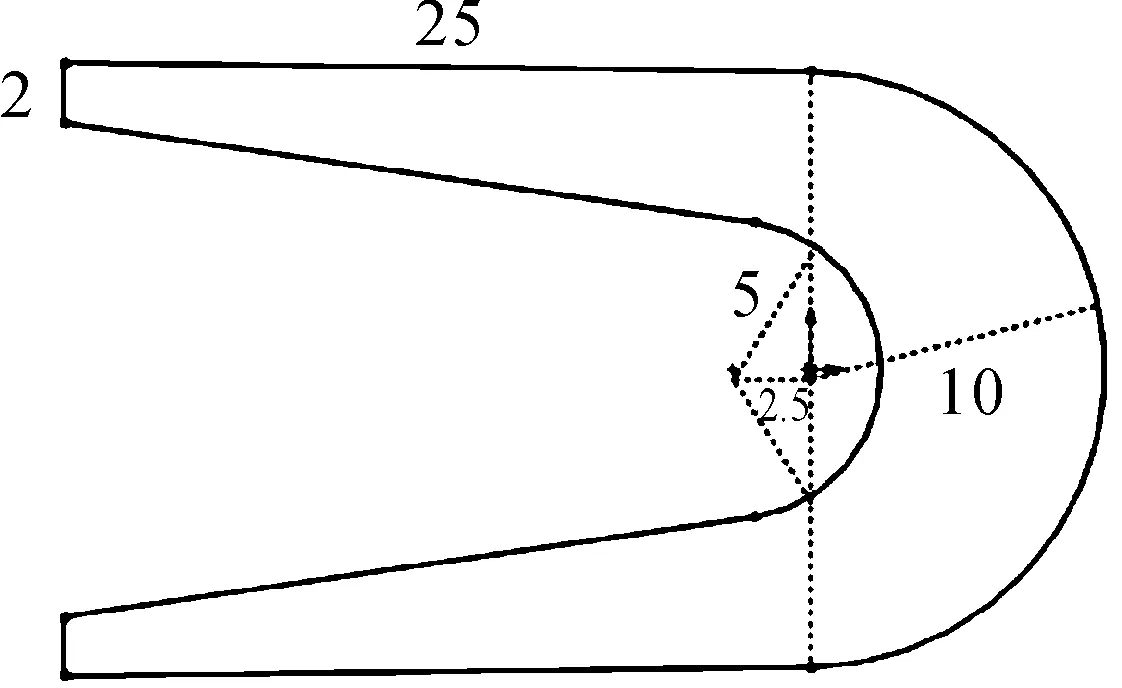
图3 电枢结构尺寸

若电枢的厚度为h，回收方向上有效截面积为A，电枢回收方向有效长度为l，则有

S·h=A·l

(4)

从电枢仿真模型可知，电枢厚度为20 mm，即h为20 mm，回收方向有效截面积A为20 mm×20 mm=400 mm2。根据式(4)，可求得U形电枢有效长度l约为16.6736 mm。

3.2 U形电枢阻力系数

利用上述仿真模型，分析不同初速下的特征衰减长度，然后计算U形电枢阻力系数。分别设置电枢速度为350 m/s、300 m/s、250 m/s，然后通过仿真得到电枢速度衰减为初速的0.368时，电枢运动的位移，如表3所示。

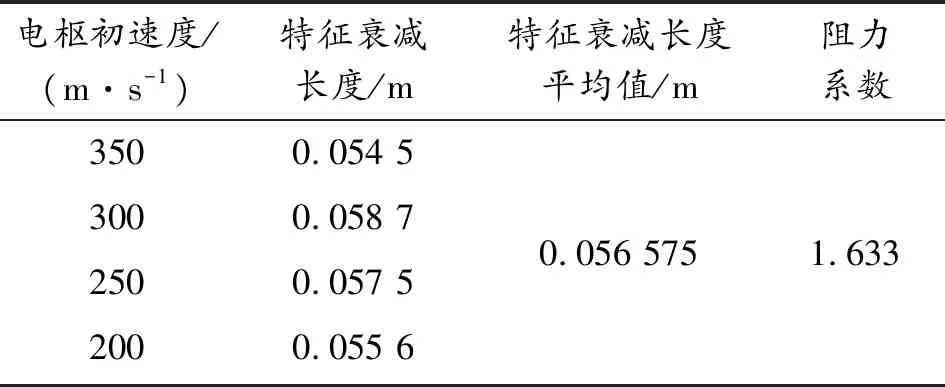
表3 不同初速度电枢特征衰减长度及阻力系数值

通过分析仿真结果可以发现，不同初速的U形电枢在同一介质中的特征衰减长度基本为一定值。当回收介质为水时，电枢特征衰减长度约为0.056 575 m，在已知电枢密度为2 770 kg/m3，电枢有效长度为0.016 672 6 m，回收介质密度为1 000 kg/m3的条件下，根据式(2)，可求得U形电枢在水中的阻力系数大约为CD=1.633。

4 U形电枢阻力系数的试验验证

为验证理论分析和数值仿真的正确性，构建了U形电枢回收试验系统，并开展了U形电枢在水中的回收试验，通过试验得到U形电枢的阻力系数。

4.1 电枢在水中运动分析

利用电磁轨道炮发射U形电枢，然后利用回收试验箱对电枢进行回收，回收试验箱中盛满水介质。为了防止实现水介质的密封，电枢发射进入试验箱的入口处采用聚氯乙烯塑料膜进行密封，如图4所示。在水的压力作用下，密封处将向外凸起。

图4 回收装置密封效果

利用高速摄影机对U形电枢在水中的运动状态进行测量，所得结果如图5所示。从图5可以看出，电枢在水介质中，运动轨迹整体向下，同时电枢本身的状态也发生了一定角度翻滚。

图5 水中电枢运动状态

分析其原因，主要是由于试验装置加工精度较低，电磁轨道炮发射的电枢弹道有一定偏差，电枢头部难以精准击中密封膜的球形凸起的中心部分。从而使得电枢刺穿薄膜时，弹道轨迹发生偏转，偏转方向与电枢头部击中球形凸起的位置有关，如图6所示。从图6可以看出，当电枢击中密封膜球形面中心时，运动轨迹不发生偏转；当电枢击中球形面下半部分时，运动轨迹会向下偏转；当电枢击中球形面上半部分时，运动轨迹会向上偏转。

图6 电枢撞击薄膜示意图

4.2 阻力系数计算

电枢位移及速度变化是根据高速摄像机拍摄到的图片分析所得，由于高速摄像机拍摄角度及试验装置本身因素，高速摄像机难以拍摄到电枢入水的整个过程，因此在求解过程中以高速摄像机第一次捕捉到的电枢速度为实际初速度。

试验中，通过速度测量装置测得电枢的初速约为333.3 m/s，而高速摄像机捕捉到的电枢初速为115.15 m/s，当电枢速度衰减为捕捉初速的0.368(即42.375 m/s)时，电枢在水中的运动距离约为0.072 m，即电枢在水中的特征衰减距离大约为0.072 m。根据式(2)，可求得该U形电枢在水中的阻力系数大约为CD=1.283。

根据仿真结果求得电枢在水中的阻力系数值约为1.633，而根据试验结果求得的阻力系数值约为1.283，两者之间存在一定的误差。分析其原因，主要是因为在仿真过程中，不考虑电枢重力的影响，电枢在水中的运动轨迹是一条平稳的直线，电枢始终头部朝前，阻力值相对稳定。验证试验时，电枢运动轨迹发生了一定偏转，同时电枢本身发生了翻滚，虽然最后还是头部向前，但在翻滚过程中所受到的阻力会比未翻滚状态下小，因此所求得的阻力系数值也会偏小。

5 结论

通过理论分析、数值仿真和验证试验，分析了U形电枢在水介质中的阻力系数。通过研究可以看出：利用水介质可以实现低速电枢的无损回收；U形电枢在水中的阻力系数大约为1.283。由于密封膜的凸起的原因，导致试验值比仿真结果偏小，但总体上基本一致，从而验证了仿真模型的有效性。