NaCl共晶盐相变球堆积床气流蓄冷特性

陆毅，涂平，张后雷

（1.南京理工大学，南京 210094；2.深圳大稳科技有限公司，广东深圳 518000）

相变蓄冷在建筑空调、家用冰箱、食品储存等领域应用广泛。相变球堆积床是一种典型的蓄热或蓄冷系统，具有结构简单、蓄能密度大等特点。目前大多数有关相变球堆积床的研究集中于蓄热或0℃以上的蓄冷应用，有关低温蓄冷球堆积床的应用相对较少。例如，吴双茂等[1]研究了载冷剂为乙二醇水溶液和蓄冷剂为水的堆积床，建立了传热模型并分析了不同载冷剂流速对堆积床蓄冰率的影响。康艳兵等[2]对相变蓄热球体堆积床建立了传热模型，求解了沿轴向的相变界面及流体的温度分布和系统的有效传热系数、有效传热面积等随时间变化规律，并与实验结果做了对比。CHENG等[3]研究了蓄冷剂为有机溶剂、相变温度在10℃附近并填充多种蓄冷球直径的堆积床的传热性能。杜雁霞等[4]研究了板式相变储能堆积床的传热性能，得到了蓄冰速率的非稳态变化规律。

共晶盐溶液如氯化钠、碳酸钾和硝酸铝溶液等是常用的蓄冷剂，其相变潜热和导热系数较大且相变体积变化小。将共晶盐溶液封装在球壳内即形成相变蓄冷球。本文以低温（＜0℃）应用为背景，拟采用NaCl共晶盐相变球作为蓄冷剂，以空气作为载冷剂，分析相变球的蓄冷特性，为实际应用装置设计提供参考。

1 数值模型

图1为柱状垂直堆积床结构示意图，堆积床床体为圆柱体，堆积床内填充相变蓄冷球，空气从堆积床底部均匀流入给相变蓄冷球充冷。在图1中，Ds表示堆积床直径，H表示堆积床高度，d表示蓄冷球直径，r表示蓄冷球半径，x表示沿堆积床高度方向坐标轴，Ts（i，j）表示第i个单元内蓄冷球的第j层的温度，Δξ表示蓄冷球内沿半径方向微元厚度，Tc（i）表示堆积床第i个单元内空气温度，Δx表示堆积床沿高度方向微元高度。本文相变材料选用25%（质量浓度）的氯化钠共晶盐溶液，不考虑相变前后的物性变化，NaCl共晶盐溶液及固相的热物性见表1[5]。选用常压空气作为载冷剂。

1.1 物理过程

初始时刻，假设堆积床内各处温度一致。开始蓄冷时，低温空气由堆积床底部（x=0 m处）流入，冷却堆积床中的相变蓄冷球，空气从堆积床顶部（x=H处）流出。在堆积床内温度最大值小于-20℃时（稍低于相变温度），蓄冷过程结束。

表1 NaCl共晶盐溶液及固相的热物性

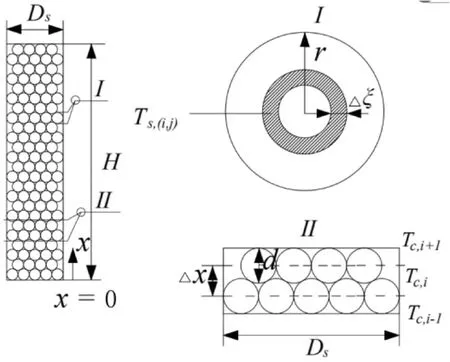
图1 柱状垂直堆积床结构示意图

1.2 数学方程

在对图1中蓄冷堆积床进行数值分析时，先做下述假设：

1）在蓄冷堆积床内，相变蓄冷球填充均匀，形成孔隙率均匀的多孔介质；

2）忽略空气沿径向的速度梯度和温度梯度；

3）相变蓄冷球球壳厚度很小，因此忽略球壳热阻及热容；

4）相变蓄冷球内仅有导热过程，相变蓄冷球间没有传热；

5）蓄冷堆积床侧壁无冷损失。

基于上述假设，空气能量守恒方程写为：

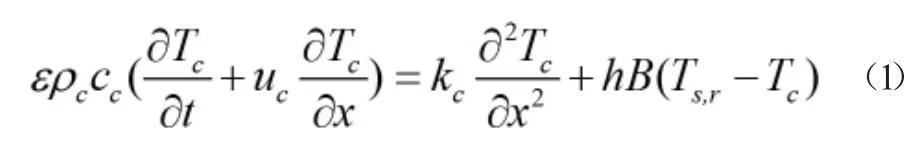
其中：

式（1）中，ε表示堆积床孔隙率，ρc表示空气密度，cc表示空气比热，Tc表示空气温度，t表示时间，uc表示空气的表观流速（空床平均流速），kc表示空气导热系数，h表示空气与相变蓄冷球之间的对流换热系数，B表示单位体积堆积床内相变蓄冷球的换热面积，Ts,r表示相变蓄冷球表面的温度。堆积床孔隙率ε按照式（3）计算[6]。

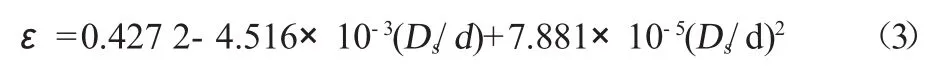
空气与相变蓄冷球之间的对流换热系数按式(4)计算[7]。

其中：

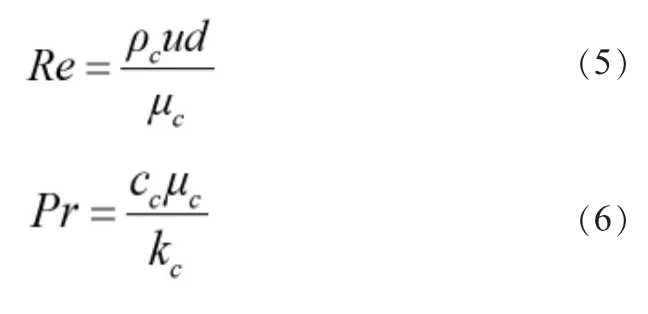
式（5）中，μc表示空气的动力粘度。

相变蓄冷球的能量守恒方程：

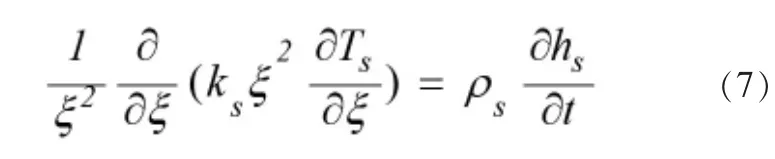
式（7）中，ks表示相变蓄冷球的导热系数，Ts表示相变蓄冷球温度，ρs表示相变蓄冷球密度，hs表示相变蓄冷球的比焓。在数值分析过程中，堆积床内初始条件如式（8）所示：

式（8）中，To(0，x)表示堆积床的初始温度。

当空气由堆积床底部（x=0 m处）通入时，边界条件如式（9）和（10）所示：

式（9）和（10）中，Tc（n，x=0）表示空气入口温度，Tc（n，x=H）表示n时刻上边界处空气温度。

堆积床的蓄冷量按式（11）计算[3]。

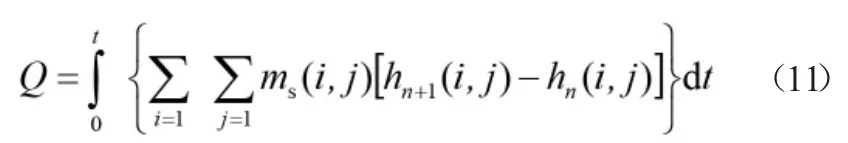
式（11）中，Q表示一定时间内的总蓄冷量，ms（i,j）表示相变蓄冷球微元的质量。

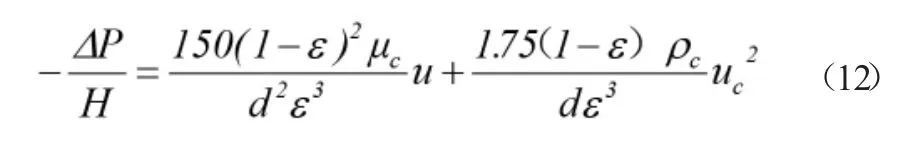
堆积床空气进出口压降如下计算[8]：

1.3 求解方法

式（1）和式（7）采用显示格式离散，即下一时刻的温度分布由上一时刻的温度分布递推得出。经过网格无关性验证，沿堆积床高度方向划分20个网格，沿蓄冷球半径方向划分10个网格，时间步长取0.05 s。采用Visual Basic 6.0编写计算程序求解。

2 结果分析

2.1 堆积床内温度分布

定义堆积床高径比β=H/D，对于一个H=1 m，D=0.25 m的堆积床，β=4。图2所示为开始蓄冷后，堆积床内沿堆积床高度方向温度变化。图中表示空气的质量流量。图2（a）与图2（b）分别表示空气、相变蓄冷球表面温度随时间的变化，系统开始运行后，堆积床内空气温度迅速降低，并与相变蓄冷球发生对流换热，相变蓄冷球表面也迅速降低；越靠近入口（x=0 m）处空气温度降低越快。图2（c）所示为相变蓄冷球球心温度随时间的变化，Ts，0表示相变蓄冷球球心温度，相变蓄冷球内传热过程为导热过程，相变蓄冷球内氯化钠溶液温度由初始值逐渐降低至-19.2℃附近，当温度到达-19.2℃后，体系内开始发生相变，释放潜热，固液相共存，过程中温度保持恒定，直至完全凝固为固相后继续释放显热。当蓄冷进行到约11 h时，堆积床顶部(x=0.975 m处)相变蓄冷球球心温度降至-20℃以下，即完成潜热蓄冷过程。

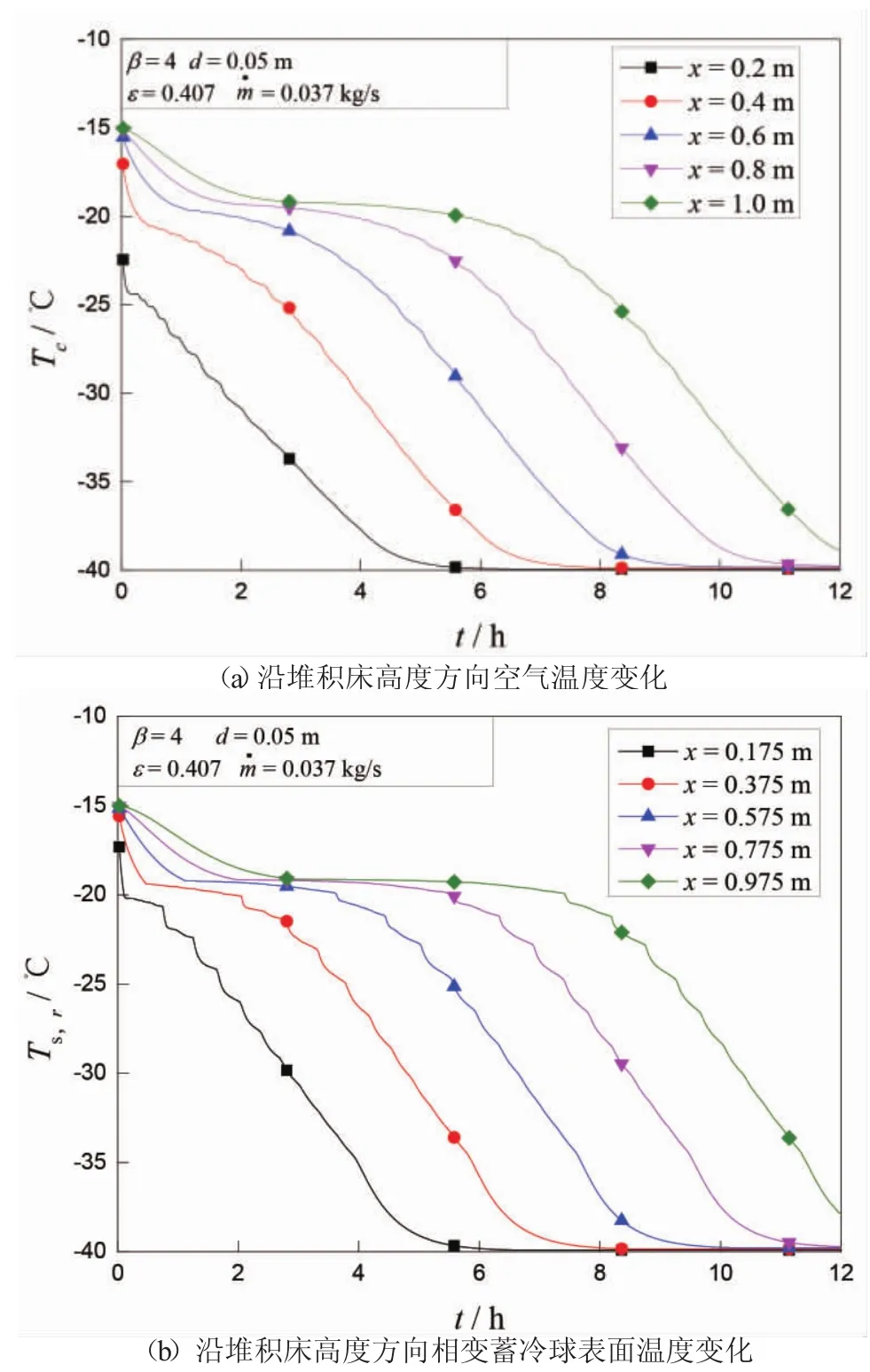
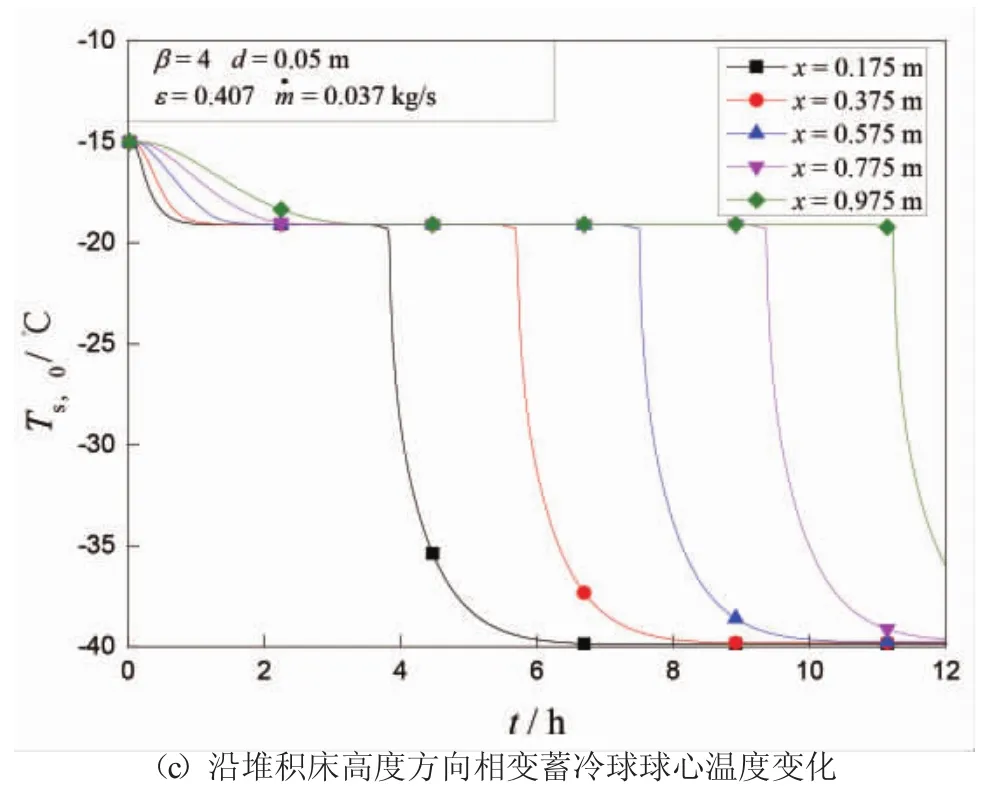
图2 堆积床内沿堆积床高度方向温度变化

2.2 堆积床设计参数对蓄冷量的影响

图3给出了在堆积床底部通入低温空气后，相变蓄冷球直径分别为0.01 m、0.02 m、0.04 m和0.05 m时堆积床内蓄冷量随时间的变化。在0～1.5 h内，4种球径对应的蓄冷量差别不明显。运行1.5 h后，相变蓄冷球直径d为0.01 m所对应的蓄冷速率明显提高，其它3种球径下的蓄冷量仍差别不大。直到运行8.5 h后，球径为0.02 m的相变蓄冷球对应的蓄冷速率明显大于球径为0.04 m与球径为0.05 m下的蓄冷速率。运行9 h后，球径为0.01 m的堆积床内蓄冷量基本不变，曲线斜率趋近与0，蓄冷过程基本结束，而球径为0.02 m的堆积床，在运行10 h后，蓄冷量曲线斜率才趋近与0。在计算截止点（11 h）附近，小球径对应的堆积床蓄冷量高于大球径下的堆积床蓄冷量,这是因为不同的相变蓄冷球直径对应不同的堆积床孔隙率，蓄冷球直径较小时，孔隙率也较小，蓄冷球质量更大，故而蓄冷能力也更大。为了获得更大的蓄冷量，应该选用更小的蓄冷球直径。

图3 不同相变蓄冷球直径下堆积床内蓄冷量随时间的变化

图4给出了在相同堆积床体积、相同蓄冷球直径和不同高径比条件下，堆积床蓄冷量随时间的变化情况。六种堆积床高径比对应的孔隙率差别很小，因此可忽略孔隙率的影响。结果表明：在空气质量流量和相变蓄冷球直径一定的条件下，当蓄冷时间足够长时（即完成潜热蓄冷开始进入显热蓄冷后），堆积床内总蓄冷量差别不大；而在潜热蓄冷过程中，β值越大，堆积床蓄冷速率越小，即相同时间内，堆积床蓄冷量越小。这是因为不同高径比下堆积床孔隙率差别很小，而堆积床体积一定，相变蓄冷球质量差别很小，在相变蓄冷球全部完成相变后，堆积床的总蓄冷量差别很小；而在堆积床潜热蓄冷过程中，β值越大，堆积床高度越大直径越小，沿堆积床高度方向蓄冷球个数越多，单个蓄冷球前后温差越小，蓄冷速率就越小。

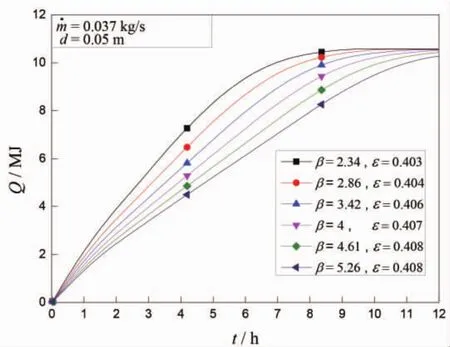
图4 堆积床蓄冷量随时间的变化情况

图5分析了不同空气质量流量对堆积床蓄冷性能的影响。结果表明，堆积床入口处空气质量流量越大，堆积床蓄冷速率越大。这是因为质量流量越大，空气与蓄冷球之间的换热越好，蓄冷球降温越快，堆积床蓄冷速率就越快。例如，在给定堆积床尺寸和相变蓄冷球直径的条件下，当空气质量流量为0.022 kg/s，蓄冷时间为11 h时所对应的蓄冷量，对于空气质量流量为0.029 kg/s的运行工况只需要8 h蓄冷时间即可达到，蓄冷时间缩短了约27.3%。

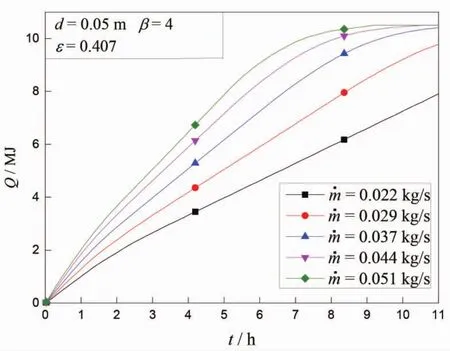
图5 不同空气质量流量对堆积床蓄冷量性能的影响

在堆积床的设计过程中，需要考虑进出口压降的影响，该值将直接影响到输送风机耗功。图6对比了4种蓄冷球直径下，堆积床的进出口压降。该图结果表明，蓄冷球直径的变化对堆积床进出口压降影响较大。这是因为蓄冷球直径越小，堆积床孔隙率越小，进而产生了较大的单相流动阻力，进出口压降就越大。蓄冷球直径从0.02 m减小到0.01 m，孔隙率减小了5%，堆积床进出口压降增加到原来的2.57倍。图7给出了相同空气质量流量和蓄冷球直径条件下，不同堆积床高径比对应的进出口压降。堆积床高径比越小，堆积床进出口压降越小。堆积床高径比从2.34增加到3.42，进出口压降增加了25%。图8所示为不同空气质量流量对进出口压降的影响。可以看出，质量流量越大，流动阻力越大，堆积床进出口压降越大。对于堆积床进出口压降而言，蓄冷球直径是最大的影响因素。

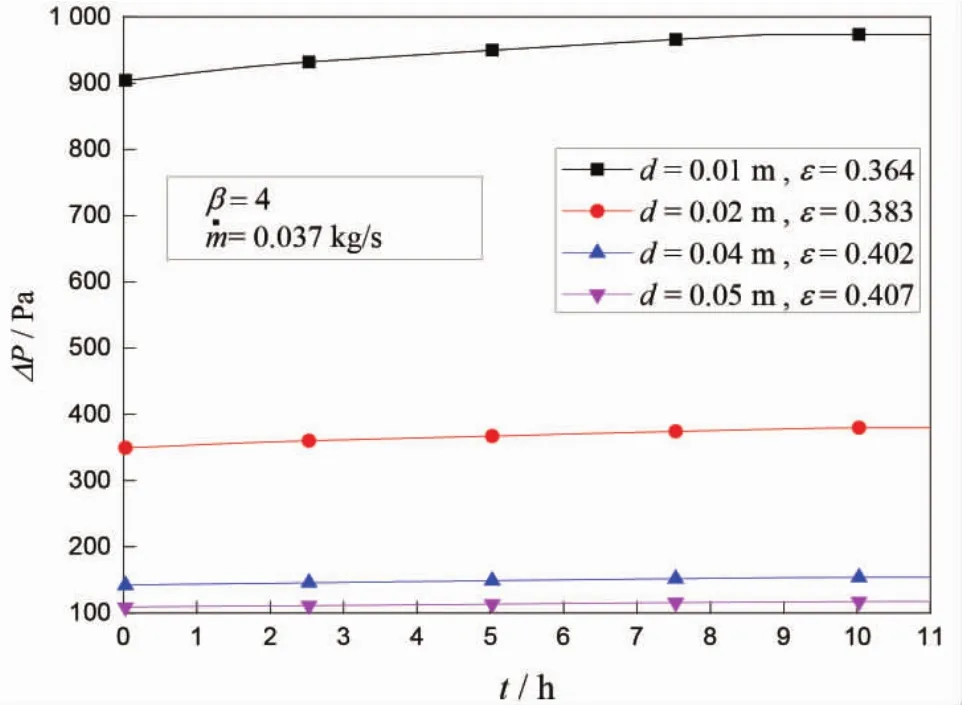
图6 不同蓄冷球径下堆积床的进出口压降

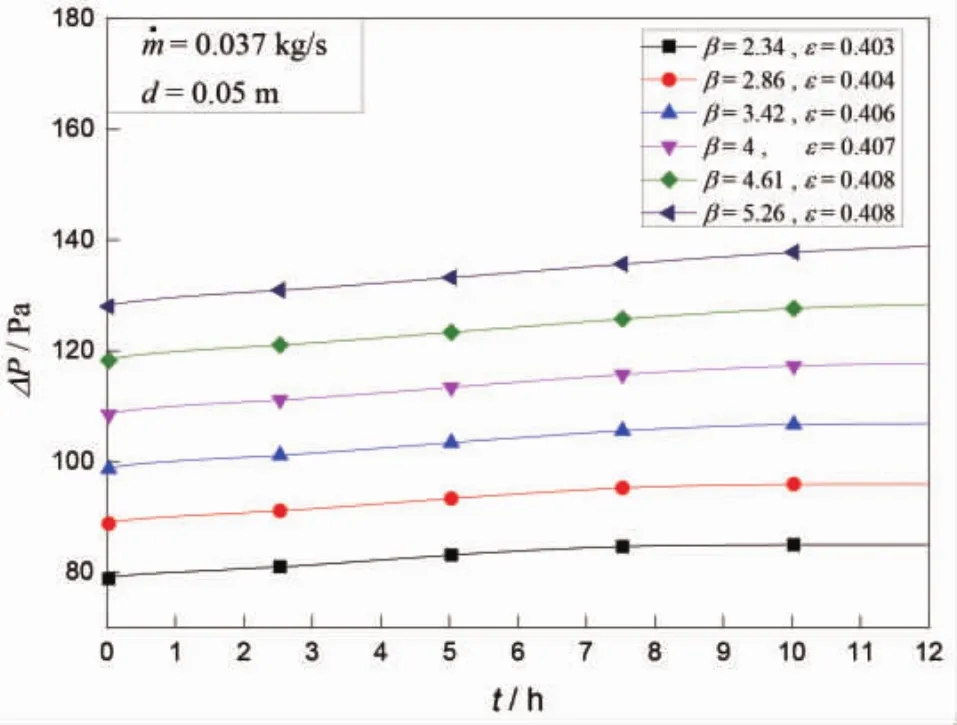
图7 不同堆积床高径比对应的进出口的压降

图8 不同空气质量流量对进出口压降的影响

3 结语

本文对低温相变球堆积床的蓄冷特性进行了计算分析，该堆积床采用空气为载冷剂，氯化钠共晶盐溶液为蓄冷剂。计算结果表明：在相同的堆积床体积下，减小蓄冷球直径和增加入口空气质量流量均有助于提高堆积床蓄冷速率，但会同时增大空气压降；减小堆积床长径比可以同时提高堆积床蓄冷速率并减小空气压降，但需要注意的是本文并未考虑空气入口处的分配问题，对实际的堆积床，堆积床长径比减小，就意味着入口空气分配器所占的体积就会越大（本文未加考虑），因此，必须加以综合权衡。此外，采用低温共晶盐蓄冷时还存在其它一些影响性能的因素（如过冷问题），具体设计时也需考虑[9]。