小学数学数形结合思想的培养策略探讨

王金浬

【摘 要】数学作为小学的三门主要学科之一，具备较强的系统性与逻辑性等特点，因此对于刚刚步入校园的小学生来说具有一定的难度。因此本文结合笔者自身的教学经验，从小学数学教学的特点入手，针对目前小学数学教学中数形结合思想的应用提出几点建议，以供参考。

【关键词】小学数学;数形结合;思想;培养;策略

【中图分类号】G623       【文献标识码】A

【文章编号】2095-3089（2019）06-0288-01

一、引言

数形结合思想作为一种新型教学手段，在教学中的运用越来越普遍，它主要是通过“数”与“形”之间的相关转换以及相互对应来帮助学生解决数学中遇到的问题的一种思想。这种教学方法之所以受到欢迎，是由于它不仅能使复杂的问题简单化，同时还可以将抽象的数学问题转化为更为形象，解决数学问题可以达到事半功倍的效果。小学阶段的学生正处于身心发展的关键时期，教师应当把握好这个重要阶段，充分开发学生的思维，在数学教学过程中有意识的融入数形结合思想，全面提升学生的思维能力与数学教学效果。

二、小学数学的特点

1.小学数学的入门就是从直观、形象的图像开始的。

由于小学生思维发展还不够成熟，认知水平还处于较低的阶段，对于一些抽象的图形或者是符号很难充分理解，往往需要一个较长的学习过程。例如在小学一年级学习数字的过程中，教师常常借助具体物品的数量来开发学生对数字的认知，这也让学生对数字的感觉更加真切。在古代，人们最初用石子与贝壳来进行记事，这与指导小学生学习数字的教学过程有一定的相似之处，都是基于将学生从形象思维导向抽象思维的一个过程，数形结合思想便是完成这种“无缝对接”的有效教学方法。

2.小学生“数形结合”意识的现状分析。

小学生对于具体事物的兴趣远远大于抽象事物，因此图片往往能够激发学生的学习兴趣，帮助学生更好的理解题意，因此数形结合思想在教学中具有很大的优势。目前数学教材不再细分代数以及几何，作为一门综合性的学科数学更加注重学生思维能力的发展，数学知识离不开数形结合思想，现代的学生更加善于从图形与实际物体中观察和收集重要信息，发现其中的关系，由此看来数形结合思想也时刻在为学生学习数学知识而服务着。

三、数形结合思想在数学学习过程中的优势所在

著名数学家华罗庚曾说：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休”。这句话可以充分显示出数形结合在解决问题过程中的作用与优势。要想培养学生的数形结合思想首先要让学生了解什么是数形结合，数形结合就是将学生学习的数量关系与空间形式进行结合的过程，在这个过程中学生可以打开自己的思维，从一个更加开阔的角度去思考问题和解决问题。如果一个问题变成了一个图形，那么学生的思想便可以从整体上认识和把握这个问题，从而创造性的思索解决问题的方式，这种方式就是将数的概念转化成形的概念，然后将数带入到形当中去，从而更加直观的观察两者之间的关系，对于问题的解决具有十分重要的作用。

四、小学数学数形结合思想的培养策略

1.利用数形结合激发学生的兴趣。

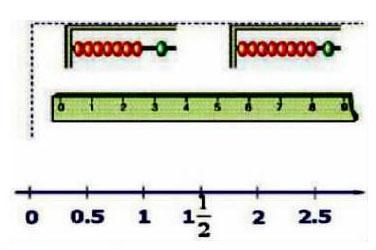
小学生在刚刚接触数学的过程中对数学中抽象的问题无法做到深入的理解，在应用知识的时候十分的被动，尤其是在理解题目意思的时候常常会出现问题。如果教师选择直观且形象的图片来展示教学内容，同时注重内容的生活化，让枯燥的教学更加贴近学生的生活，能够更好的吸引学生的注意力，學起来更容易。例如在指导一年级的学生学习数字时，教师可以用直线上的点直接建立起图形与数字之间的联系，同时直线也可以明确表现出数的有始无终、有序性等性质。其实，在这个过程中，直线上的点就是我们数形结合思想中所强调的形，通过一条直线、一个点，学生自觉的就参与到了数学学习的过程中，提升了教学效果。

2.运用数形结合思想解决复杂问题。

在高段数学的学习过程中，学生接触到的数学问题越来越复杂，简单的加减乘法已经很难帮助他们而解决这些问题，因此，学生就要从题设背景出发去寻找线索。通常情况下，学生遇到较为复杂的问题往往不知所措、无从下手，这时候教师便可以借助图形来帮助学生解决问题。以追及问题求解为例，这种题目条件复杂，常常因为速率的不同而出现各种情况，学生如果没有深入理解题目信息很难解决问题。在解决这种复杂的题目时教师可以让学生将题设进行全面的分析，然后将其中的数据写下来，引导学生寻找其中的数量关系，用直线段表示题目中的主题，在利用其中的数据进行分析，借助线段与数据的配合追及过程中相遇次数很容易就判断出来。通过这样的方式，用简单的图形和数据将复杂的数学问题变得十分简单，学生可以更快地解答难题，提高解题效率。

3.运用数形结合发展学生的思维能力。

培养学生的思维能力是数学教学过程中一项十分重要的任务，学生的认知是由规律的，由表面到抽象，由感性到理性，表象感受到概念的形成需要一个直观的反应，因此教师可以利用表象引发学生的思考，让学生在这个阶段充分发挥想象力。例如在学习百分数的习题时，有这样一个练习题：参加羽毛球兴趣小组的学生总共有80人，其中男生占其中的60%，在不断的练习之后又加入了一些男生，这时候男生占总人数的2/3，那么请问后来加入了多少男生呢？教师可以先把这道应用题中的数量关系转化为图形，通过图形可以分析出：如果我们把总人数80个人分为五份，那么男生就是3份，女生就是2份，所以现在的总人数就是6份，加入的男生为6-5=1份，得加入的男生为80÷5=16（人）。从这题不难看出：“数”、“形”互译的过程，通过这种方法学生可以更直观的看到数量之间的关系，从而进行过程推导，有效的激发了学生的解题的兴趣，提升了思维能力。

五、结语

总之，数形结合思想对于学生数学思维能力的发展十分关键，教师应当加以重视，全面提升教学水平，促进学生的全面发展。

参考文献

[1]张艳红.数形结合思想在小学数学教学中的应用[D].山东师范大学，2016.

[2]张启凤.“数形结合”思想在小学数学教学的应用研究[D].四川师范大学，2016.