旋转受限相互作用玻色系统的相变温度及基态粒子占据率

李玉山， 刘红艳， 王 磊

(菏泽学院物理与电子工程学院,菏泽 274015)

1 引 言

以往对旋转玻色气体激发态对应的热力学性质的研究多数考虑的是旋转效应[1]、空间维度[2]、粒子数密度[3]、有限尺度效应[4]等外在因素的影响，相互作用项的影响很少涉及.实际上，原子间的相互作用总是存在的，而且相互作用的强弱以及相互作用的形式往往也会对热力学性质产生重要影响，从而使得势阱中旋转相互作用玻色气体的玻色-爱因斯坦凝聚(BEC)相变温度和基态粒子占据率等物理量不同于无相互作用的旋转理想玻色系统[5, 6].

调研发现，对简谐势阱中存在弱相互作用的玻色气体热力学性质的研究多采用的是局域密度近似方法[7, 8].本文试图将该方法推广到简谐势阱中的旋转弱相互作用玻色气体，进而推导出存在弱相互作用的旋转玻色气体的BEC相变温度和基态粒子占据率的解析表达式，并讨论粒子间相互作用的影响.最后，将计算结果与旋转理想玻色气体进行对比.

2 理论模型

(1)

3 合成磁场中的弱相互作用玻色气体

准经典近似下，系统的粒子数为

(2)

式中的nε为处于ε能级的粒子数，可写为

(3)

粒子数密度为

(4)

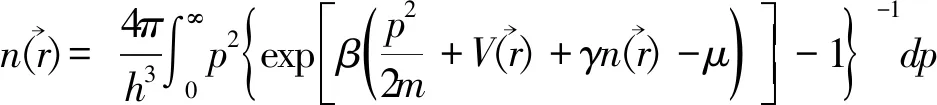
(5)

(6)

包含基态粒子贡献的系统粒子数表达式为

(7)

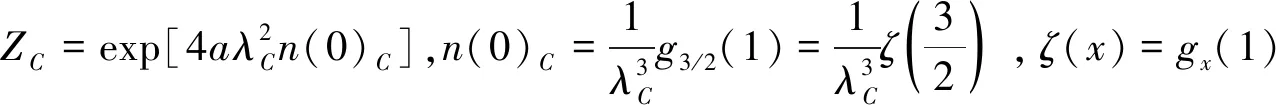
(8)

(0)C-n(r))]}

(9)

因此，粒子数可写为

(10)

积分后可得

(11)

由此可得TC为

(12)

(13)

式(12)和式(13)相除可得

(14)

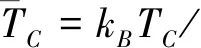
图1 散射长度对BEC相变温度的影响Fig.1 Effect of scattering length on the BEC transition temperature

下面求基态粒子的占据率.处于激发态的粒子数为

(15)

(16)

图2给出了几种不同散射长度下的基态粒子占据率随温度的变化曲线.由图2可以看出，基态粒子占据率曲线对弱相互作用的依赖关系非常微弱，这种影响几乎可以忽略.这就意味着，弱相互作用的修正是个微小量，式(16)中的λ十分接近λC.

图2 不同散射长度a对应的基态粒子占据率随温度的变化Fig.2 Ground state fraction versus temperature with different scattering lengths a

在式(16)中，若令a=0，则有

(17)

式(17)与简谐势阱中旋转理想玻色气体的基态粒子占据率表达式获得了很好的吻合[6, 11].

4 旋转框架中的弱相互作用玻色气体

采用同合成磁场相类似的推导方法，可求得弱相互作用玻色子处于旋转框架中的各物理量表达式，具体如下

(18)

(19)

(20)

(21)

(22)

进一步的分析可知，对于旋转框架的情况，散射长度对BEC相变温和基态粒子占据率的影响规律和合成磁场的情况基本相同，不再赘述.同样地，若令a=0，则式(18)—(22)均能够与无相互作用的旋转理想玻色气体的表达式获得很好的吻合.

5 结 论

基于局域密度近似，研究了合成磁场和旋转框架中的受约束弱相互作用玻色子的BEC相变温度和基态粒子占据率.结果表明，在散射长度为零时，弱相互作用消失，旋转弱相互作用玻色气体相变温度和基态粒子占据率的解析结果回归到无相互作用的旋转理想玻色气体的形式.本文的结果对于进一步了解旋转BEC的基本特征，特别是粒子间相互作用对热力学性质的影响具有重要意义.