利用啁啾激光调制分子谐波信号

冯立强, 刘 航, 李 义

(1. 辽宁工业大学 理学院， 锦州 121001； 2. 辽宁工业大学 化学与环境工程学院， 锦州 121001； 3. 中国科学院大连化学物理研究所分子反应动力学国家重点实验室，大连 116023)

1 引 言

强激光场驱动分子辐射分子高次谐波辐射(molecular high-order harmonic generation, MHHG)作为一种非常重要探测分子内电子运动以及产生孤立阿秒脉冲的方法被广泛研究[1-3]. 关于强激光驱动原子辐射高次谐波的过程可由半经典的‘电离-加速-回碰’三步模型[4]来描述. 但不同于原子体系，当激光驱动分子体系时，由于分子多出的核自由度，分子中电子的电离以及回碰与原子相比有很大的不同. 对于电离过程，研究人员在较大核间距离处发现H2+可以发生电荷共振增强电离[5]、多光子共振电离[6]甚至离解态电离[7]. Bian等[8]发现在不对称分子中，由于长寿命激发态的作用，电子在HeH2+中会发生激光诱导电子跃迁过程. 对于回碰过程，由于分子中不只有一个原子核，因此加速电子理论上有几率与任何一个原子核回碰，因此导致谐波辐射在不同原子核之间的分布. 例如：Feng等[9,10]理论研究了H2+以及HeH2+谐波辐射的空间分布以及激光参数对其分布的影响. Lein等[11]发现由于双H核之间的干涉相长以及干涉相消现象导致了谐波光谱上呈现极大以及极小值.

一般来说，由上述电离和回碰所引起的分子谐波辐射现象可以分为两类：即，谐波振幅变化和谐波频率变化. 具体来说，关于谐波振幅变化，Lein[12]发现分子谐波辐射强度与分子自相关函数有关. Feng等[13]研究表明分子谐波辐射强度与分子质量，激光强度，激光脉宽都有关系. 关于谐波频率变化，Bian等[14]和Liu等[15,16]发现H2+光谱在低强度和高强度激光场下呈现谐波红移和蓝移，并且随着激光脉宽和振动态增大，红移现象被减弱，蓝移现象被增强.

虽然，近年来对分子谐波辐射过程的研究取得了很多进展[5-16]，但是激光波形多采用对称高斯型，近年来随着啁啾激光场的发展，啁啾激光驱动原子、分子辐射高次谐波得到了广泛关注[17, 18]. 因此，本文理论研究了啁啾激光对H2+谐波辐射的影响.

2 计算方法

强激光场与H2+相互作用的含时薛定谔方程为[19, 20],

(1)

(2)

(3)

其中，mp、R、z分别为核质量、核与电子坐标.E、ω1、τ、α为激光场场强、频率、脉宽和啁啾参数.α> 0表示正啁啾；α< 0表示负啁啾.

高次谐波表示为：

(4)

3 结果与分析

图1(a)给出了H2+在5 fs-400 nm(10个光学周期)激光场驱动下辐射高次谐波的谱图. 激光场强为I= 4.0×1014W/cm2. 一般来说，由于激光场的对称性，谐波光谱只呈现奇次谐波. 但是，在核与电子耦合的作用下，谐波辐射呈现红移. 并且，在正向(例如：α= 0.0003)和负向(例如：α= -0.0003)啁啾激光场的调控下，谐波红移分别得到增强和减弱. 表1给出H2+在上述啁啾激光场驱动下谐波光谱在高能处的强度. 从表中数据看出，谐波辐射强度在正向和负向啁啾场驱动下分别被减弱和增强. 图1(b)-1(d)给出无啁啾、负向啁啾、正向啁啾激光包络图，H2+电离几率以及H2+在其驱动下辐射谐波的时频分析图[21]. 由三步模型可知，在激光场的上升区间(dI(t)/dt> 0)，由于激光强度的持续增强，后电离的电子会获得更多的能量，进而导致谐波光谱的蓝移；相反在激光场的下降区间(dI(t)/dt< 0)，由于激光强度的持续减小，后电离的电子将获得较低的能量，进而导致谐波光谱的红移. 观察图1(b)-1(d)可知，当α= 0.0时[图1(b)]，谐波辐射强度主要来源于激光下降区间，因此导致谐波光谱呈现红移. 当α= -0.0003时[图1(c)]，由于激光上升区间电离几率的增大，谐波辐射强度被增强，因此导致谐波红移减弱. 当α= 0.0003时[图1(d)]，激光上升区间的谐波辐射强度被减弱，但是激光下降区间谐波辐射强度得到增强，因此导致谐波辐射主要贡献来自激光下降区间，这是导致谐波光谱红移增强的原因. 分析谐波辐射过程可知，高阶谐波主要由3个谐波辐射能量峰贡献产生，记为P1～3. 当引入负向啁啾参数时，P1强度被增强[图1(c)]，因此导致谐波辐射强度增大；但当引入正向啁啾参数时，P1强度被减小，因此导致谐波辐射强度减弱.

表1 H2+在激光强度为I= 4.0×1014W/cm2的啁啾激光场驱动下谐波辐射强度

Table 1 The harmonic yields of H2+driven by the chirped pulses withI= 4.0×1014W/cm2.

啁啾参数(α)0.0-0.00030.0003谐波强度2.1×10-47.2×10-49.3×10-3

图2(a)给出了上述激光场在I= 1.0×1015W/cm2时驱动H2+辐射高次谐波的谱图. 由图可知，当α= 0.0时，谐波辐射呈现蓝移. 并且，随着正向(例如：α= 0.0003)和负向(例如：α= -0.0003)啁啾激光场的引入，谐波蓝移分别减弱和增强. 表2给出H2+在上述啁啾激光场驱动下谐波光谱在高能处的强度. 从表中数据看出，H2+在高强度啁啾场与低强度啁啾场驱动下的谐波辐射强度呈现相似的趋势，即，在正向和负向啁啾场驱动下分别被减弱和增强. 图2(b)-2(d)给出无啁啾、负向啁啾、正向啁啾激光包络图，H2+电离几率以及H2+在其驱动下辐射谐波的时频分析图. 由图可知，当α= 0.0时[图2(b)]，由于激光强度的增大，激光上升区间电离几率增大，因此导致激光上升区间的谐波辐射强度增强，这是谐波辐射呈现蓝移的原因. 当α= -0.0003时[图2(c)]，激光上升区间电离几率继续增大，进而导致谐波辐射主要来源于激光上升区间，因此导致谐波蓝移增强. 当α= 0.0003时[图2(d)]，激光上升区间的谐波辐射强度被减弱，但是激光下降区间谐波辐射强度得到增强，因此导致谐波光谱蓝移减弱. 分析谐波辐射过程可知，由于激光强度的增大，高阶谐波主要由4个谐波辐射能量峰贡献产生，记为P0～3. 当引入负向啁啾参数时，P0和P1强度被增强[图2(c)]，因此导致谐波辐射强度增大；但当引入正向啁啾参数时，P0和P1强度被减小，因此导致谐波辐射强度减弱.

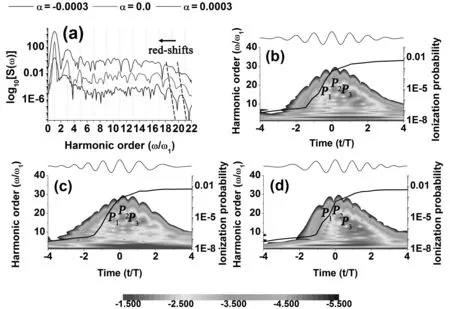
图1 (a) 5 fs-400 nm激光场驱动H2+辐射谐波. 激光强度为I = 4.0×1014 W/cm2. 激光包络图，H2+电离几率以及H2+在其驱动下辐射谐波的时频分析图 (b) α = 0.0；(c) α = -0.0003；(d) α = 0.0003. Fig. 1 (a) Harmonic spectra from H2+ driven by the 5 fs-400 nm pulse with I = 4.0×1014 W/cm2. The laser profiles, the ionization probabilities and the time-frequency analyses of the harmonics from H2+ for the cases of (b) α = 0.0; (c) α = -0.0003; (d) α = 0.0003.

表2 H2+在激光强度为I= 1.0×1015W/cm2的啁啾激光场驱动下谐波辐射强度

Table 2 The harmonic yields of H2+driven by the chirped pulses withI= 1.0×1015W/cm2.

啁啾参数(α)0.0-0.00030.0003谐波强度1.27×10-35.3×10-39.21×10-4

图3(a)给出了5 fs-400 nm无啁啾激光场在I= 1.0×1015W/cm2时驱动H2+辐射高次谐波的谱图以及双H核对谐波辐射的贡献[9]. 由图可知，在高强度激光驱动下，高阶谐波会产生劈裂，并且形成非奇次谐波，这一现象在低强度激光场下不太明显. 分析双H核谐波辐射贡献可知，高阶谐波劈裂分别来自于不同H核的贡献. 产生这一现象的原因是由于双H核谐波频移不一致所导致的不对称相消干涉引起的，即，右H核谐波辐射蓝移大于左H核谐波辐射蓝移. 图3(b)和3(c)给出了双H核谐波辐射的时频分析图. 如前所述，高阶谐波主要来自于P1～3的贡献. 对于左H核谐波辐射过程[图3(b)]，激光上升区P1的强度略大于激光下降去P3的强度，因此导致左H核谐波辐射微弱的蓝移. 对于右H核谐波辐射过程[图3(c)]，激光上升区P1的强度明显大于激光下降去P3的强度，因此导致右H核谐波辐射具有明显的蓝移现象.

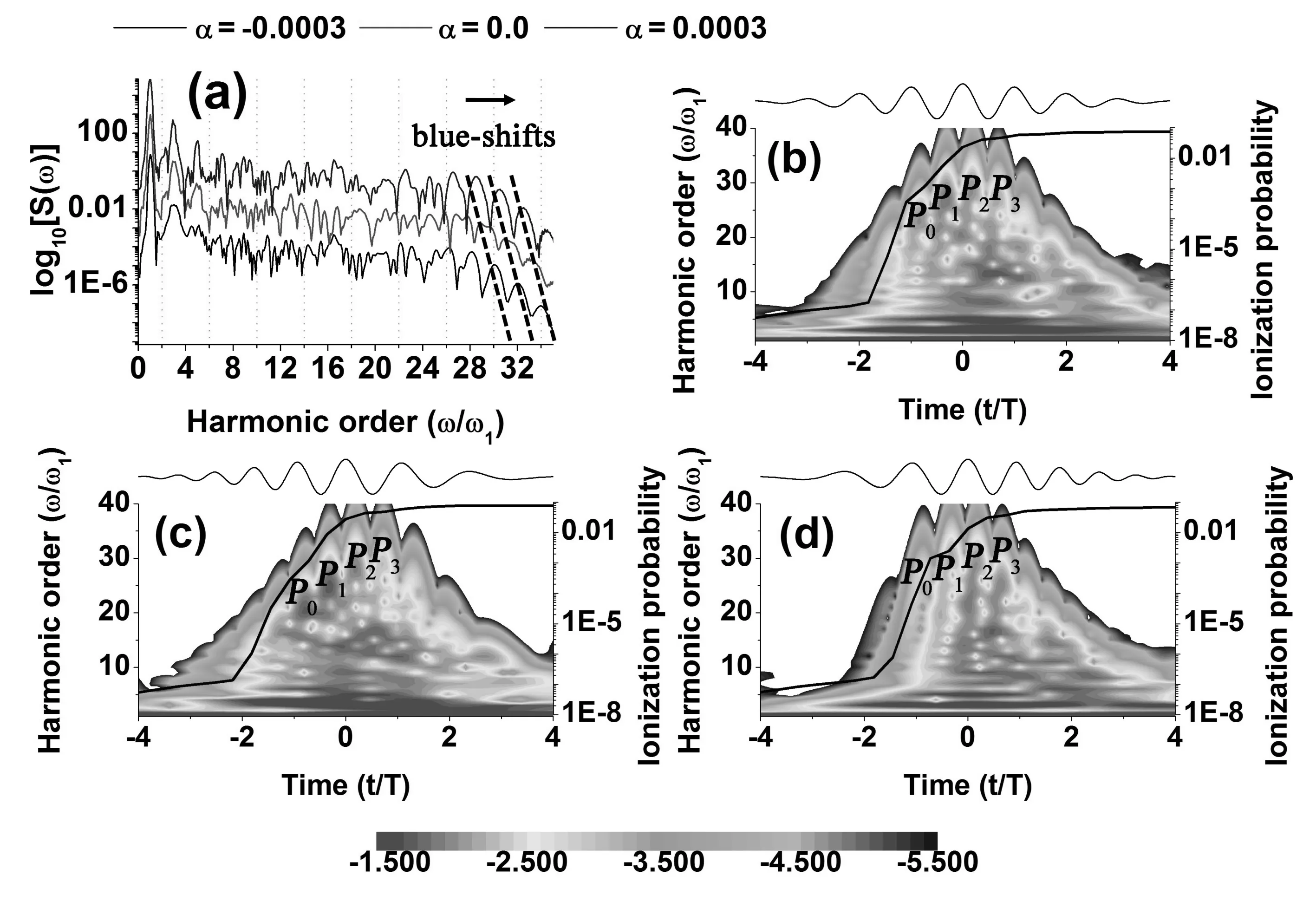
图2 (a) 5 fs-400 nm激光场驱动H2+辐射谐波. 激光强度为I = 1.0×1015 W/cm2. 激光包络图，H2+电离几率以及H2+在其驱动下辐射谐波的时频分析图 (b) α = 0.0；(c) α = -0.0003；(d) α = 0.0003. Fig. 2 (a) Harmonic spectra fromH2+ driven by the 5 fs-400 nm pulse with I = 1.0×1015 W/cm2. The laser profiles, the ionization probabilities and the time-frequency analyses of the harmonics from H2+ for the cases of (b) α = 0.0; (c) α = -0.0003; (d) α = 0.0003.

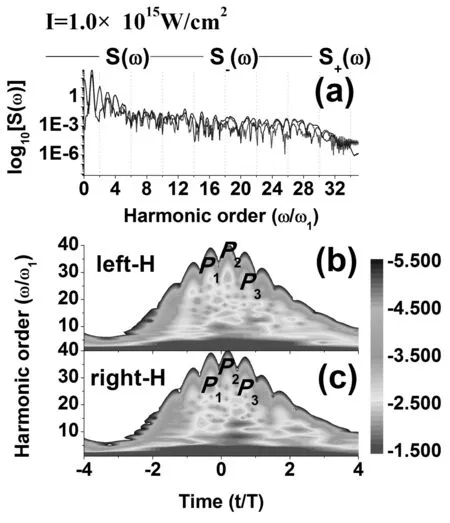
图3 (a) 5 fs-400 nm无啁啾激光场驱动H2+辐射谐波光谱以及双H核的贡献. 激光强度为I = 1.0×1015 W/cm2. 谐波辐射时频分析图 (b) 左H核；(c) 右H核. Fig. 3 (a) Total harmonic spectrum and the contributions of the harmonics from the two-H nuclei driven by the 5 fs-400 nm chirp-free pulse with I = 1.0×1015 W/cm2. The time-frequency analyses of the harmonics from (b) left-H and (c) right-H.

4 结 论

综上所述, 本文理论研究了啁啾激光对H2+谐波辐射的影响. 结果表明，引入正负向啁啾参数后低强度激光下谐波红移被增强和减弱；而高强度激光下谐波蓝移被减弱核增强. 并且，谐波辐射强度也在正负啁啾调控下得到减弱核增强. 在高强度激光下，谐波光谱呈现非奇次谐波. 其产生原因来自于双H核频移不一致所导致的不对称相消干涉现象.