鸡蛋缓冲包装跌落冲击力学仿真及验证
李 昭曹萌萌,2孙建明李华杰
(1. 河南科技大学,河南 洛阳 471023;2. 陕西华丽包装有限公司,陕西 咸阳 713800)
鸡蛋具有较高的营养价值,作为人类主要的食物及营养来源,需求量呈逐年上升的趋势[1]。鸡蛋从产出到消费者手中,需经过收集、分类、清洗、包装、检验、加工、运输、储存、交易等多道环节,其中造成鸡蛋破损的主要为装卸环节、运输环节。有关资料[2]显示:鸡蛋在生命周期中的破损率为10%~17%,其中蛋产出时的破损率仅占2%~3%,而在流通过程中造成的破损率达9%~12%。缓冲包装设计是避免鸡蛋在流通过程中发生破损最为有效的技术手段。目前市场上投入使用的鸡蛋缓冲包装多种多样,仅以EPS为材料的鸡蛋缓冲包装结构就不下10种,当不合格的包装投入市场使用后,不能在流通环节对鸡蛋形成有效的保护,会造成较大的经济损失[3]。因此,为使蛋品产业更加合理化,降低鸡蛋破损率,有必要对鸡蛋的物理特性及鸡蛋缓冲包装在运输过程中的力学性能进行研究,以优化鸡蛋缓冲包装。
对缓冲包装优化设计的方法主要有试验法和有限元仿真分析法,传统的试验法虽然能获得较为真实的缓冲效果,但试验周期长、效率低且投入较大,而利用有限元仿真分析,可快速获得不同变量条件下包装件的定量缓冲效果,有针对性地进行实验验证,缩短设计周期,提高设计效率。有限元仿真分析作为一种有效的技术手段,已被广泛用于包装各个领域的研究,其研究方法也得到了相关技术人员的一致认可。但目前对于鸡蛋的仿真分析大多只针对蛋壳进行单一分析,忽略了蛋液对蛋壳的影响,且对鸡蛋的破损条件确定也缺乏明确的试验方法[4-5]。
EPS具有质轻、抗震、防摔、成本低、保护性能好等特点,被广泛应用于产品缓冲包装;EPE俗称珍珠棉,具有无毒、高弹性、环保等特点,是目前常见的缓冲包装材料之一[6]。本试验拟以鸡蛋缓冲包装常用的EPS、EPE缓冲材料为研究对象,选用ABAQUS仿真分析软件[7],采用流固耦合模型研究鸡蛋缓冲包装系统力学性能,并设计一种鸡蛋破损条件确定的试验方法,以期为鸡蛋缓冲包装提供设计依据。
1 材料与方法
1.1 材料与仪器
1.1.1 材料
鸡蛋:按GB/T 21710—2016规定对散装鲜鸡蛋进行抽样,以同一规格产品为一个批次,同一批次鸡蛋挑选新鲜且质量、形状、大小相似的,购买后立即送往实验室,并确保鸡蛋表面无损伤;
EPS(试验前未作为缓冲包装使用):密度11 kg/m3,生产地金华;
EPE(试验前未作为缓冲包装使用):密度20 kg/m3,生产地上海。
1.1.2 仪器与设备
微机控制电子式万能试验台:WDW-100型,济南正中试验机制造有限公司;
双臂跌落试验机:HD-ADJ520-1型,东莞市海达仪器有限公司;
辅助固定装置:实验室自制,由于试验平台为光滑平面,在试验过程中需对鸡蛋进行固定,采用薄PVC自制鸡蛋固定装置,对试验结果影响较小,如图1所示。

1. 微机控制电子式万能试验台 2. 鸡蛋 3. 辅助固定装置
1.2 试验方法
1.2.1 研究流程 如图2所示,首先对鸡蛋强度进行测试,为有限元分析提供评价标准;然后对有限元建模中3个主要因素(跌落冲击过程、流固耦合、分析步长)进行分析,确定相关参数后建立有限元模型;以鸡蛋强度测定试验得到的强度指标为依据,对仿真结果进行分析并得出仿真结论(即缓冲厚度适宜范围);最后进行跌落试验,当符合验证要求时表明仿真结果可满足缓冲要求,否则应优化有限元模型重新进行仿真。
1.2.2 鸡蛋强度测定 为确保鸡蛋在搬运及运输过程中发生跌落时缓冲包装的缓冲性能满足设计需求,需要确定鸡蛋的破损强度[8],为有限元仿真提供评价指标。以GB/T 8168—2008包装用缓冲材料静态压缩试验方法为参考,对鸡蛋进行强度测定试验。将试验鸡蛋分为3组,每组5颗,共计15颗鸡蛋进行强度压缩试验,对试验鸡蛋进行分组编号。利用微机控制电子式万能试验台测得鸡蛋压缩过程中力—时间曲线,由此得出蛋壳在不同破损阶段承受的最大力,通过等效接触面积计算出蛋壳破损时承受的强度值。

图2 研究流程
1.2.3 设计应力的计算 鸡蛋破损过程大体分为裂纹破损、小面积破损和大面积破损3个阶段。由于鸡蛋存在一定的个体差异,其破损值在一定范围内分布,为保证设计结果的安全性,取每阶段试验最小力值作为此阶段的破损力F,并在设计计算时取一定的安全系数a,等效接触面积S通过实际测量获得,则设计应力计算公式为:
(1)
式中:
σ——设计应力,MPa;
F——破损力,N;
S——等效面积,mm2;
a——安全系数。
2 结果与分析
2.1 鸡蛋强度确定
鸡蛋强度试验最终破损情况及力—时间曲线如图3所示。经观察分析:当力—时间曲线出现第1个峰值时,鸡蛋出现第1条裂纹;当力—时间曲线出现第2个峰值时,鸡蛋出现多条裂纹;当力—时间曲线出现第3个峰值时,鸡蛋发生面破损。通过对15组鸡蛋强度试验的试验数据进行分析得出:当施加载荷力为5.3~6.0 N时,蛋壳出现裂纹;当力达到10.0~15.6 N时,蛋壳出现小面积破损;当力达到20 N以上时,出现大面积破损。由于出现裂纹的鸡蛋在长时间的运输过程很容易受到外界细菌的污染从而导致鸡蛋腐败变质,因此在本次试验过程中,认定鸡蛋蛋壳上出现裂缝即视为鸡蛋破损。测量得到鸡蛋与万能试验台的接触面积近似为1 mm2,由公式(P=F/S)计算出鸡蛋出现裂纹时,蛋壳上受到的应力值P=5.3 MPa。
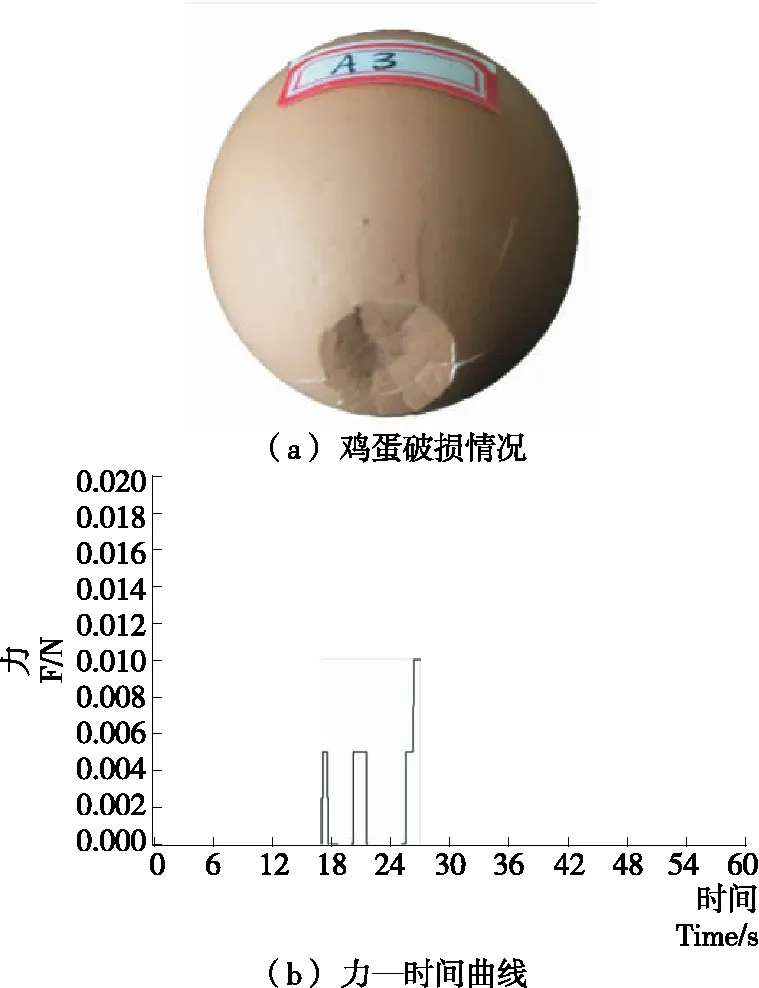
图3 试验数据
2.2 鸡蛋跌落缓冲仿真模型构建
2.2.1 跌落冲击过程 包装件在运输、装卸及搬运过程中极易发生跌落而受到跌落冲击的作用,跌落冲击是一种瞬时能量转换的形式,在极短的时间内速度、位移、力或加速度发生突然的变化[9]。本试验主要通过有限元仿真模拟包装件在流通过程中发生自由跌落的现象,考察缓冲包装对跌落冲击的抵抗性能。跌落冲击有2种表现形式,本试验主要针对垂直跌落冲击进行研究。在跌落冲击过程中,发生时间极短,整个过程中会产生较大的加速度,导致包装件在一瞬间承受极大的冲击力,对产品造成损伤,包装件跌落过程如图4所示。
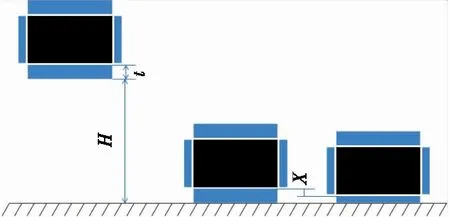
图4 包装件跌落力学模型
理想状态下,在跌落过程中忽略包装件所受摩擦力及空气的阻力,包装件重力势能全部转化为缓冲结构的变形能和包装件的动能,这一过程的运动规律表示如下[10]:
(2)
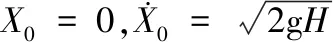
(3)
式中:
F——作用在缓冲结构上的力,N;
m——包装件的质量,kg;
X——缓冲结构的变形量,mm;
W——包装件的重力,N。
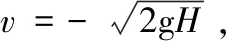
2.2.2 流固耦合力学模型 由于鸡蛋的蛋壳较薄,在跌落过程中,蛋液(液体)将对蛋壳(固体)产生一定影响,因此本试验建立鸡蛋流固耦合模型。流固耦合力学是流体力学与固体力学交叉衍生的一门学科,主要研究结构与流体间相互作用[11]。流固耦合系统具有一定的复杂性,不能单独计算结构力学或流体力学模块,两者之间相互作用、相互影响,因此流固耦合关系应利用不同结构单元来模拟相应材料,并通过设置边界条件建立相应关系。本次仿真使用欧拉单元模拟蛋液,拉格朗日单元模拟蛋壳,两者边界产生接触,蛋液在固定的网格内流动,通过材料分布来描述蛋液的变形状态[12]。为保证在有限元分析中流固耦合问题能成功解决,流体场和结构场模型都应经过严格测试,确保每个单场都已正确定义并输入正确。
2.2.3 分析步长确定 跌落仿真分析属于力学问题,因此需创建一个显式、动态分析步,为避免计算量过大,需要设置有效且尽可能短的分析步长。本仿真首先设置初始分析步长为T=5.5E-04 s,经有限元仿真计算及后处理输出得到系统的能量图,通过系统能量图分析鸡蛋缓冲包装模型与刚性地面瞬间碰撞的时间点。图5为系统内能曲线,当T=2.5E-04 s时,系统与刚性地面发生碰撞时能量最大,因此可取T=2.6E-04 s为系统仿真分析步长,经有限元仿真验证,该分析步长可有效反应跌落过程。
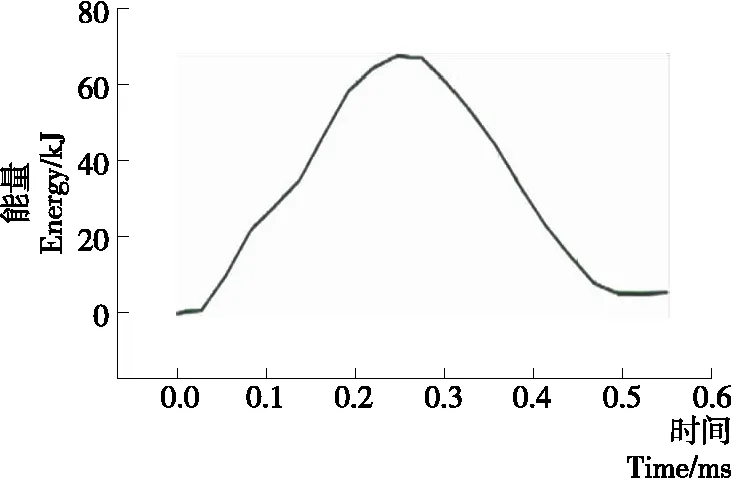
图5 系统内能曲线
2.2.4 建立有限元模型 鸡蛋蛋壳是一个薄壁体[13],组成及结构复杂,碳酸钙为其主要成分。为简化模型,忽略气室的影响,将蛋白与蛋黄视为一体,同时假设鸡蛋蛋壳、蛋液为连续均质、各向同性的线弹性系统。缓冲材料选用EPS、EPE,厚度δ分别设置为5,10,15,20,25 mm。地面设置为刚体,系统三维模型如图6所示。
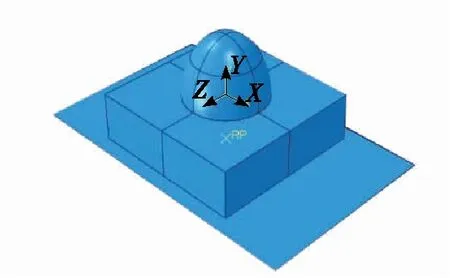
图6 鸡蛋跌落仿真系统三维模型
各材料属性见表1,其中蛋液声速为1 500 m/s,黏度为0.001 kg/m3[14]。鸡蛋及缓冲包装采用C3D8R网格,刚性地面采用R3D4网格,设置蛋壳与缓冲包装之间为绑定关系,整个模型加载重力场,赋予刚体地面边界条件为固定状态。
由于缓冲包装的最终目的为保证蛋壳不发生破损,因此仿真分析以蛋壳的等效应力为主要分析对象,研究不同鸡蛋缓冲包装的力学特征。
2.3 鸡蛋跌落缓冲仿真分析
2.3.1 同一厚度缓冲包装力学特征 不同材料不同厚度鸡蛋缓冲包装的力学特征相似。图7为5 mm厚度的EPS缓冲包装在不同跌落阶段的蛋壳受力云图。在跌落过程中缓冲包装与地面接触并发生冲击作用,冲击经由缓冲包装最先传递到蛋壳底部,随着跌落时间的延长,由于缓冲材料的变形效应,蛋壳上的应力值及应力集中区域不断发生变化。分析跌落仿真过程中蛋壳上的应力变化,可以得出:① 随跌落时间的延长蛋壳上受到的应力值逐渐增大,当跌落速度为零后应力值开始减小;② 应力集中区域首先发生于蛋壳底部,随着缓冲材料变形量的增加,蛋壳中下部出现应力集中。
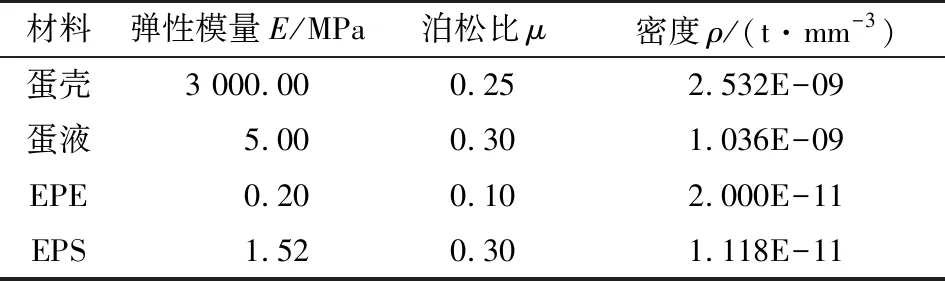
表1 材料参数[15-17]
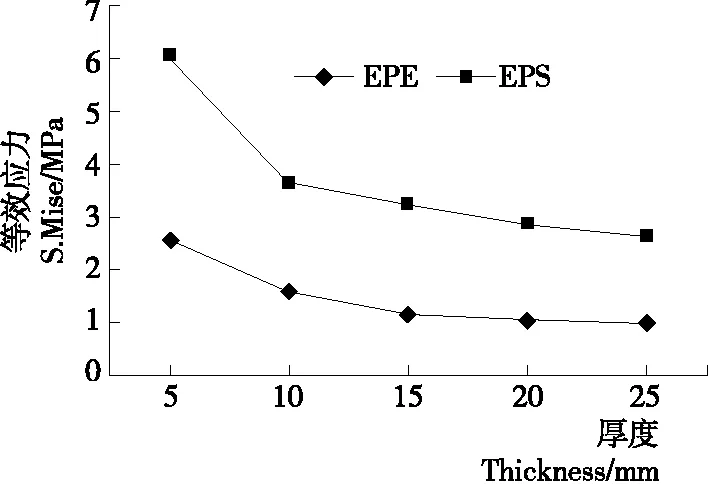
2.3.2 不同厚度缓冲包装力学特征 不同厚度下EPS、EPE仿真数据对比如图8所示。
由图8可知:
(1) 随着缓冲包装厚度的增加,2种材料蛋壳上的应力值均逐渐减小,缓冲材料厚度越大,对于鸡蛋的缓冲性能越好。
(2) 同一厚度下,不同材料蛋壳上应力值:EPE 通过强度试验及有限元仿真得出的数据是较理想条件下鸡蛋跌落冲击分析数据,在实际跌落冲击过程中,要考虑众多影响的因素,如车辆的紧急启动、制动,产品突然受强烈外力作用,以及鸡蛋蛋壳的钙化程度、表面光滑程度等,因此在实际缓冲包装设计中应取一定的安全系数,以保证设计的安全性。本试验取安全系数为2,即当应力值σ≥2.65 MPa时,蛋壳就会出现裂纹,视为鸡蛋发生破损现象。结合仿真分析数据,可以得出:采用EPE作为缓冲材料时,缓冲厚度≥10 mm即可在跌落过程中有效保护鸡蛋;采用EPS作为缓冲材料时,缓冲厚度≥25 mm 方能在跌落过程中有效保护鸡蛋。 EPS,δ=5 mm 图8 EPE与EPS仿真数据对比 采用双臂跌落试验机,设置跌落高度为1 000 mm,对仿真结果进行验证。选取EPE(δ=10 mm),EPS(δ=25 mm)分别进行20组跌落试验,试验结果中鸡蛋均未发生破损;同时选取EPE(δ=5 mm),EPS(δ=20 mm)各20组进行对比试验,在对比组试验中鸡蛋均出现一定数量的裂纹破损。结果表明,有限元仿真结果可作为EPE、EPS鸡蛋缓冲包装的设计依据。 通过试验的方法确定鸡蛋的破损强度,并利用有限元软件ABAQUS建立鸡蛋流固耦合仿真模型,研究了鸡蛋及缓冲包装在跌落冲击过程中的动态响应,对不同材料不同厚度缓冲包装的缓冲效果进行了分析。有限元仿真结果表明:同一厚度下EPE的缓冲效果优于EPS,建议选择缓冲厚度时EPE应≥10 mm,EPS应≥25 mm,可有效防止鸡蛋在跌落冲击过程不发生破损;鸡蛋在跌落过程中应力集中区域主要分布在蛋壳底部及中下部,可更有针对性地对鸡蛋缓冲包装进行优化设计。同时,通过跌落试验验证,仿真结果可有效避免鸡蛋在流通过程中由于跌落冲击发生破损。研究中为简化运算和模型,忽略了鸡蛋内部流体的不均匀性及气室的影响,在后期的研究中可继续优化模型以使仿真结果更接近于实际状况。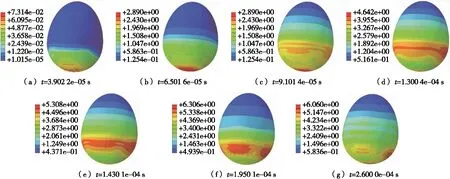
2.4 仿真结果验证
3 结论

