基于ISM法的教育技术专业必修课程分析——以文山学院为例

曹 知

(文山学院信息科学学院，云南文山663099)

0 引言

在课程体系中，根据培养目标进行课程设置和安排是一个重要的环节。除了课时、学分等因素外，还需要分析课程之间的关系。教育技术学作为一门交叉学科，课程体系有一定的复杂性，涉及到教育学、心理学、计算机科学、传播学等学科。各院校办学定位及专业师资环境不同，开设专业时有不同的侧重，课程设置也有所差异。课程体系的复杂性、差异性等因素，在实际的课程设置中依靠主观判断难以准确系统确定课程之间的层次关系。

解释结构模型法(Interpretive Structural Modeling Method)，简称ISM分析法，是Warfield在1973年提出的基于图论研究社会系统中复杂要素间关联结构的方法[1]。本文正是利用ISM分析法对文山学院教育技术学本科专业的课程设置进行分析和探讨，对主要课程的设置提供一个较为客观的参考。使用ISM法进行分析时，要经过抽出要素、决定要素形成关系、制作形成关系图的基本过程，其主要原理是根据元素已知的直接关系挖掘出背后的间接关系。在实际操作中，核心是将要素及其形成关系以矩阵形式表示，建立邻接矩阵，计算出可达矩阵，最后生成层级关系图。

1 课程要素抽出及形成关系确立

1.1 抽取课程要素

文山学院教育技术学专业培养方案，自专业开设以来有多次不同程度的调整。从2011-2017级不断进行微调，主要集中在开课学期和学时安排方面。同时，由于学校办学定位向应用型本科院校转变，2016级、2017级的培养方案相较之前版本有较大调整，减少了理论性较强课程的课时和比例，增加了一些实践性、实用性较强的课程。例如，《数据结构》课程从必修课程中删除，《常用软件使用》等课程列入必修范围等，这些改变是应用型转型中的尝试，从教师、学生的反馈来看，还需要不断的完善。整体来看，历次调整原因涉及就业导向的变化、办学定位的转变、本科教学评估的促进等方面。通过对近七届的课程计划进行分析，与专业教师及学生探讨，最终确定了其中较为稳定的专业必修课程，作为进行ISM分析的基本课程元素。

这些课程分别是：①C程序设计；②数据结构；③数据库SQL；④大学物理及实验；⑤模拟与数字电子技术及实验；⑥概率与数理统计；⑦高等数学；⑧教学系统设计；⑨教育传播学；⑩教育技术学导论；教育信息处理；网络技术与教育应用；动画处理技术；多媒体教学软件设计；信息技术教学论；计算机应用基础；计算机组装与维护；摄像与视频处理技术；摄影与图像处理技术。为方便分析，后文用课程编号代表相应课程。

1.2 确立课程要素之间的形成关系

解析结构模型法的分析过程是由具体到抽象又回归具体的过程。将具体的课程抽象化是进行数据分析的基础，这一步需要分析各课程要素之间的零散形成关系，将这些关系通过矩阵表现出来。确定形成关系时，要考虑不同课程之间的逻辑层次、上下关系。由零散关系分析到形成矩阵的过程中，可以使用关系图进行过渡，图与矩阵是互相对应的。

由于课程要素较多，互相之间的形成关系这里不做一一分析，但有一些形成关系需要根据实际情况和培养目标充分考虑。在这19门课程中，数据结构与数据库的关系方面，数据结构的学习对于深层次学习数据库有一定帮助；教育信息处理、网络技术与教育应用、多媒体教学软件设计、计算机组装与维护等课程并不是其他课程的直接低级目标。诸如此类的着重分析对于后期生成有效的课程层次结构十分必要，在生成层次结构之后，还可以根据情况返回这一步重新修正一些关系。本文在确定形成关系的过程中，进行过多次往复修正，最终课程要素之间的形成关系综合反映在邻接矩阵A(表1)中。这一邻接矩阵反映的是课程之间的直接形成关系，表示两门课程之间存在长度为1的通路。

表1 课程元素的直接形成关系矩阵

2 解析生成层级结构

邻接矩阵的确立是之后一系列分析的基础，从课程元素之间的邻接关系中挖掘更深层次的关系是另一项关键内容。从图论角度来看，这一层操作的本质是寻找元素之间的其他通路，反映在矩阵上是由邻接矩阵求解可达矩阵的过程。

2.1 求可达矩阵

可达矩阵的求解，有不同的方法，都具有一定的计算量。本文在由邻接矩阵A到可达矩阵M的计算中，引入除对角线外其他元素均为0的单位矩阵I，当满足(A+I)≠(A+I)2≠...≠(A+I)k-1=(A+I)k时[1]，可达矩阵M=(A+I)k。具体计算中可以使用Warshell算法来求解[2]，在计算时使用C语言实现，其核心语句如图1所示。

图1 求解可达矩阵的算法

最终计算出可达矩阵M(表2)。可达矩阵表示要素之间是否存在通路，这里并不考虑路径长度。由邻接矩阵到可达矩阵的转变，挖掘出了课程元素之间的间接形成关系[3]。

2.2 解析层级关系

为了生成层级结构，需要先对可达矩阵的数据进行分析。可以用集合的方式处理，定义两个集合R(si)和A(si)，si代表课程元素。R(si)表示从si出发可能达到的全部要素集合，称为可达集合。A(si)表示所有可能达到si的要素集合，称为先行集合[3]。求出层级关系的过程可以转换成一层层抽出顶级元素的过程，顶级元素的一个最大特征是不能到达自身之外的其他任何元素。表现在集合关系上，满足R(si)∩A(si)=R(si)。

根据可达矩阵M可以得到相应的R(si)、A(si)、R(si)∩A(si)三个集合(表3)，下一步是逐层抽出最高层级元素的过程。

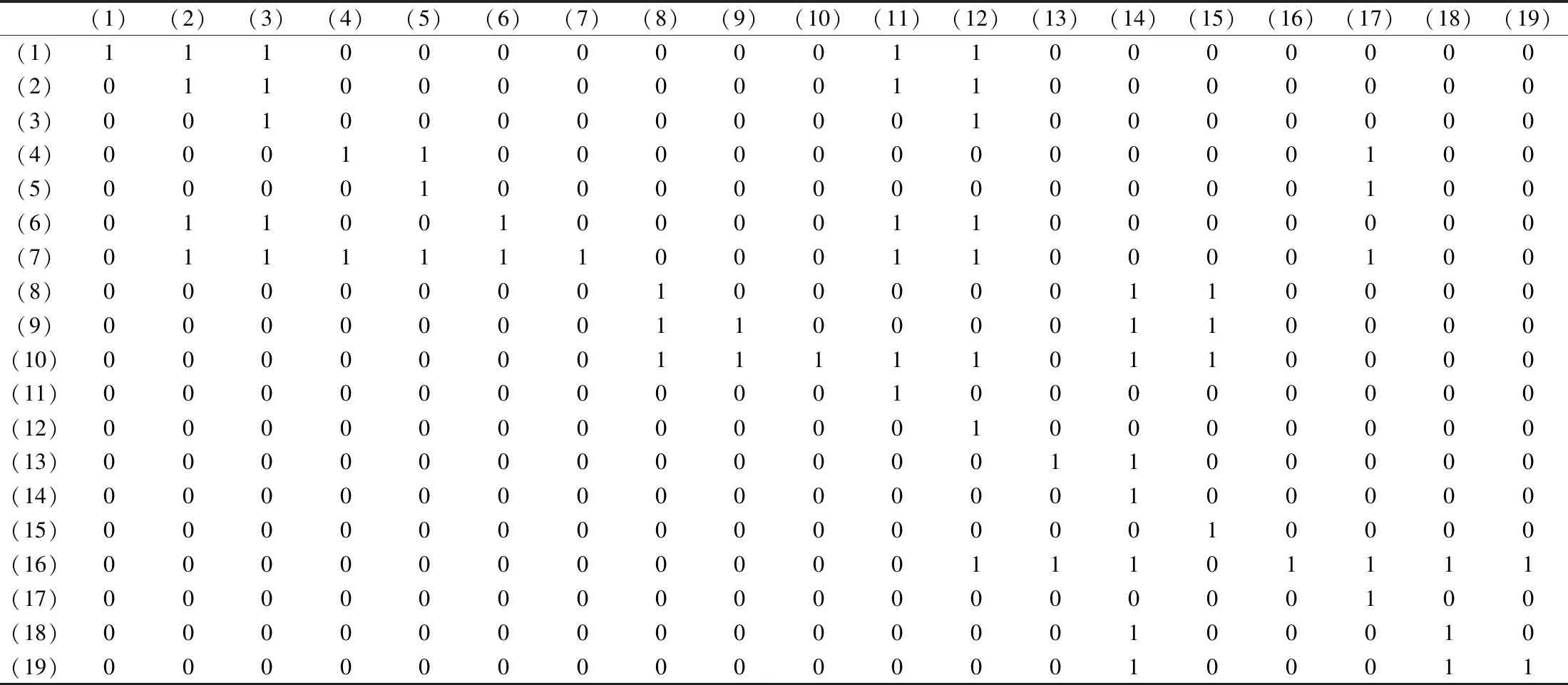
表2 可达矩阵M

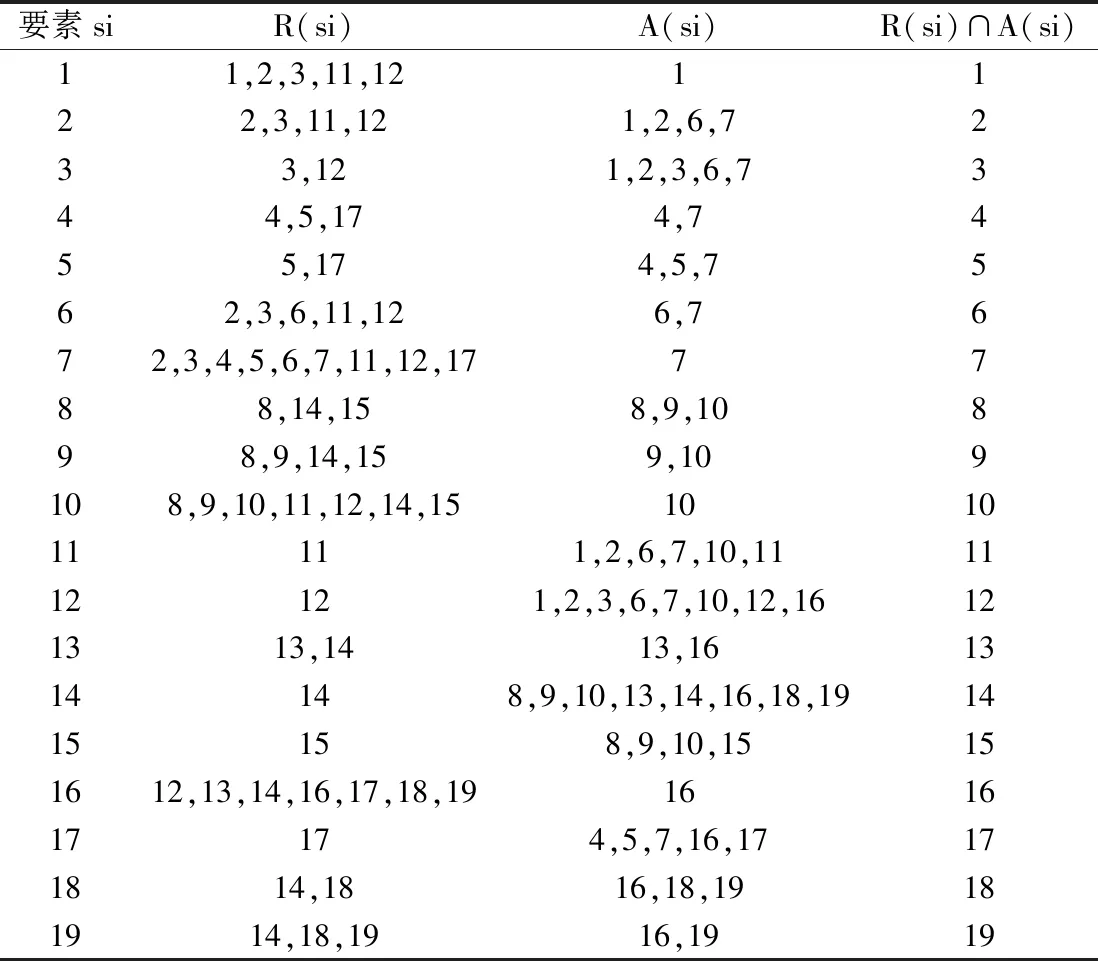
表3 可达矩阵的R(si)、A(si)与R(si)∩A(si)集合

2.3 生成层级结构

从表3中逐轮寻找满足R(si)∩A(si)=R(si)的元素，每轮筛选得到的元素均从三个集合中剔除。如第一轮，满足条件的元素有11、12、14、15，这四个元素是系统中的最顶级元素，将这四个元素记下并从R(si)、A(si)、R(si)∩A(si)这三个集合中删除。所有元素均被抽出之后，19个元素分成一个五层的结构(表4)，也就形成了19门教育技术专业课程的层级结构。

表4 课程元素层级结构

从层级结构可以看出，19门课程中，高等数学是最基础的，教育信息处理、网络技术与教育应用、多媒体教学软件设计、信息技术教学论课程的前驱课程较多或难度较大。在层级结构的基础上，结合邻接矩阵中的直接形成关系(表1)，可以绘制层级有向图。在绘制过程中，可以根据课程要素的实际内容，进行必要的分析和研讨，确立要素在有向图中的呈现位置。但是本文中课程要素较多，层级有向图的直观性减弱，实用性降低。鉴于课程总体层级已明确，相邻层之间的关系更具有参考价值，据此可以得出相邻层次之间的关系图谱(图2)，图中省去了非相邻层元素之间的关系。

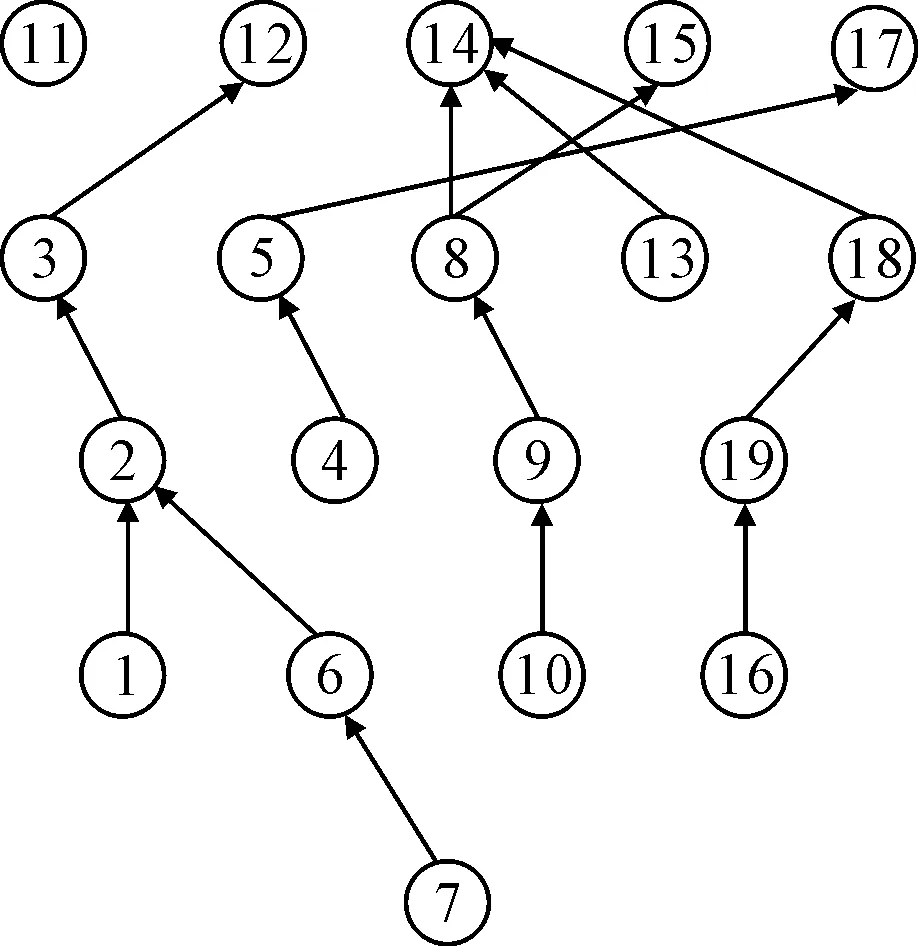
图2 课程元素层级结构关系

由于抽取元素时采取了由顶层到底层的原则，课程元素整体层级优先向上层浮动，从而使课程安排更为谨慎。例如，不考虑跨层元素之间关系的前提下，元素1、10、16其实可以和7一同安排在最底层。如果在最初抽取元素时按照从底层到顶层的顺序，1、7、10、16最终会在同一层。综合考虑严谨性和实际操作性，安排课程时，位于低层级的课程开设时间不能早于高层级的课程。

在安排教学序列时，处于层级结构低层的课程优先，同一层次内的课程，直接低级子目标较多的优先[4]。比如，最低层的高等数学(元素7)应是所有课程中最先安排的，最高层的四门课程中，多媒体教学软件设计(元素14)的相邻层直接子目标有3个，可以先安排。

3 结语

经过ISM法分析，文山学院教育技术学专业19门必修课程分为五个层级。课程元素层级直接关系图中的几个教学序列较为清晰反映了基本的学科体系。其中有一定纵深的教学序列分别为：7-6-2-3-12(程序设计)，4-5-17(物理)，10-9-8-14(教学系统设计)，16-19-18-14(媒体技术)。如果更进一步，从元素之间的路径长度和路径数量方面入手，可以更为细致地分析层级之间元素的关系强弱。当然，实际课程安排还要考虑课时量、学期等因素。

ISM法分析课程体系时，主要涉及课程要素之间的学习层级关系(上下级关系)，并未将与课程设置相关的影响因素都纳入考虑范畴，课程设置问题没有完全转变为一个系统化模型，该方法具有一定的局限性，但对于优化课程体系安排依然有其参考价值。这种方法的主要优点是，既考虑了课程之间的客观关系，又纳入了教师和课程规划人员的教材观、课程观等主观经验和认识，并实现了结构化、形象化的呈现。