功能脑网络规模对特征选择及分类的影响研究
刘鸿丽 秦小麟 曹锐 陈俊杰 刘峰 郭浩

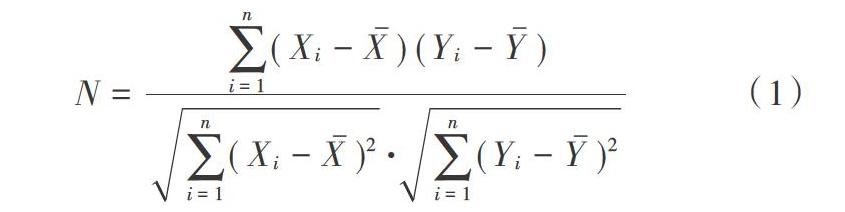

摘要:功能脑网络中不同的模板定义导致网络规模差异极大,进一步影响所构建网络的结构及其拓扑属性。但是,在机器学习方法中网络规模差异是如何影响特征选择策略及分类准确率并不清楚。研究中采用5种不同节点规模的模板进行脑网络构建,在此基础上选择脑网络的三个局部特征用SVM方法构建分类器进行抑郁症患者的识别。结果表明,节点规模较大的模板的分类准确率较高;同时,在不同节点规模下传统的P值的特征选择方法均是可行的,但其阂值设置过于严格。
关键词:功能脑网络;特征选择;特征分类;节点规模;分类器;实验分析
中图分类号:TN915-34;TP181
文献标识码:A
文章编号:1004-373X( 2019) 24-0158-05
0 引言
近年来,随着功能脑网络研究的深入,越来越多的研究人员发现功能网络的丰富拓扑结构信息可用作各种神经精神类疾病的生物学标志[1-2]。而所提取的网络拓扑特征被广泛应用于分类模型的构建中,以此进行脑疾病的辅助诊断。先前的研究中所选择的拓扑属性特征通常包括全局属性、局部属性[3]、社团结构[4]等。一些研究人员提出了新的网络特征分析方法,并应用在脑疾病的机器学习研究中,如超图”,、高序网络、最小生成树[6]、频繁子图[7]等。脑网络拓扑属性特征为磁共振影像与机器学习的结合研究提供了新的视角。
目前,这个领域仍在探索阶段,许多方法论的问题有待解决。其中一个重要的问题便是如何进行合理的模板选择以定义网络的节点。先前的研究发现,采用不同的脑网络分割模板而导致的不同的节点规模,对所构建网络的结构及其拓扑属性会产生很大的影响。此外,节点规模对网络的影响还体现在以网络拓扑属性作为特征的分类中。将不同节点数量中网络的异常特征应用到机器学习中,也会对分类准确性造成影响。在为数不多的研究中,文献[8]用AAL-90(90个节点)和AAL-1 024(1 024个节点)两个模板研究抑郁症患者的识别性能,结果发现AAL-1024模板的识别性能优于传统模板AAL90;文献[9]用AAL(90个节点)和LPBA40(54个节点)两个模板来研究脑模板和特征选择对阿尔茨海默病预测的影响,得到的结论是节点数量少时分类准确率低。前人研究验证了网络节点数量会对分类准确率产生影响,而且他们的结论是一致的:节点数量多的模板的准确率是要高于节点数量少的模板。但是,上述工作存在的潜在问题是使用的模板数量不多(只有两个),结果缺乏可对比性。此外,上述研究选用了P值作为特征选择方法(阈值设置为0.05或0.01),忽略了其他特征对分类的可能贡献。
在此背景下,本文以抑郁症为疾病模型,采用5个不同节点分割,分别构建、分析静息态功能脑网络并提取具有组间差异的网络局部拓扑属性作为可判别性分类特征应用到分类器,研究节点规模对于特征选择策略、分类准确率的影响。
1 实验材料
研究中共有66名被试,其中有38名首发、无用药、重度抑郁症患者作为抑郁组,28名年龄性别匹配的健康志愿者作为对照组。实验前同每位参与者(对照组与本人,抑郁组与家属)均达成了书面协议。被试的基本信息如表1所示。表中,数据范围为最小值至最大值(平均值+标准差);HAMD为24项汉密尔顿量表值;aP值由双样本双尾T检验获得;bp值为由双尾皮尔逊卡方检验获得。
研究中数据的采集工作是在山西医科大学第一医院完成的,所有的扫描工作由熟悉磁共振操作的放射科医生来完成。在扫描的过程中,要求被试闭眼、放松、不去想特定的事情,但要保持清醒不能睡着。扫描的参数如下:射频重复时间(TR)=2 s,存储矩阵=64 mmx64 mm,回波时间(TE)=30 ms,层间间隔=0 mm,层厚=4.0 mm,成像视野(FOV)=192 mmx192 mm。使用DPARSF软件进行数据预处理。首先弃除头动大于3 mm或转动大于3。的被试数据,然后根据标准的EPI模板将图像在MNI标准空间上进行空间标准化,最后进行线性去模糊和低频带通滤波( 0.01-0.10 Hz),以降低低频漂移及高频的生物噪声。
2 脑网络的构建
每个被试的脑网络构建过程包括节点定义与边的定义。
2.1 节点的定义
采用K-means聚类算法得到不同节点数量的分割模板。K-means聚类的随机种子体素法是基于AAL模板细分大脑区域,以定义不同的分割。具体方法如下:
1)选择250个,500个,1 000个和1 500个节点作为预期节点数目。用原始的90个节点的AAL模板,总共获得5个不同的分割模板。
2)计算原有AAL模板中每个脑区占所有脑区的体素比例V。然后,得到AAL原有脑区可细化的子区域的个数k= VN。
3)在原有脑区中设置k个随机种子体素S=S1,S2,…,Sk。然后计算一个新的体素v与所有的后个种子体素之间的距离。
4)计算距离后,将当前体素v与最近体素si结合,定义新的子区域,将v和si的物理中心设置为新的种子体素。
5)重复上述步骤,直到全脑的所有體素都分开为止。此时,大脑区域被分成k个区域,当所有脑区完成划分后,即可得到预期节点规模Ⅳ下的脑区划分。
研究完成了5种节点规模的定义,标记为AAL90,Parc256,Parc497,Parc1003和Parc1501。前缀AAL旨在表示原始的AAL模板,前缀Parc表示使用上述算法确定的模板。
2.2 连接定义和阈值选择
采用皮尔逊相关系数计算两个节点之间的平均相关系数,表示两个节点之间的相关性,进一步作为网络中节点之间边的定义。通过对每个节点的平均时间序列的计算,产生Ⅳ×Ⅳ相关矩阵。这里,Ⅳ是给定分割中的节点的数量,数学定义如下:n表示模板中的节点数量。
在目前的研究中,根据预定的阈值,将相关矩阵转换成二进制矩阵。通过稀疏度S进行阈值设置,5是实际存在的边数与可能存在的最大边数的比值。稀疏性定义方法在以前的类似研究中广泛采用。为了在统一的空间内进行比较,采用90个节点下的阈值空间S( 5%,40%)为标准,并且在该阈值空间内以步长为0.5的所有稀疏度下,构建所有被试的脑功能网络,每个被试均有8个不同稀疏度的网络。
2.3 网络指标
网络指标是从不同层面刻画网络的拓扑属性。在当前的研究中,选择了三个局部指标,包括度、节点效率和中间中心性。
2.3.1 度
度为脑网络中与该节点之间有连接的节点总数,表示该节点在脑网络中的连通性。节点i的度k(i)数学定义为:
网络中节点m与节点n有多条连接路线。式中:σmn表示节点m与节点n连接中的最短路径的条数;σmn(i)表示节点m与节点n的连接中经过特定节点i的最短路径的条数。
为了表征指标在完整稀疏度空间下的整体特性,本文计算了每个指标的曲线下面积(Area Under theCurve,AUC)。AUC提供了一种测量网络节点属性在不同稀疏下总的变化强度的方法。该方法已应用在研究中,同时有过相关报道,并被证明其对脑网络拓扑属性的改变是非常敏感的。AUC的数学公式如下:
3 特征选择及分类器
本文研究中选择度、中间中心度和节点效率三个局部指标作为特征。为了找到特征的最优子集,避免过度拟合,提升模型性能,更快地训练分类器,需要在分类前进行特征选择。选择统计显著性P值作为分类特征选择方法(P<0.05,FDR校验)。
由于SVM方法对小样本数据具有良好的分类效果,选择它作为分类器[10]。它是基于Matlab的LIBSVM工具包进行分类,并且使用10折交叉验证(10-FoldC ross Validation)的方法来评估分类器的泛化性能。具体的过程是将所有的被试随机分成10等分,逐一将其中的一等分作为测试集,剩余的9等分是训练集,最后对10次结果的均值作为对分类器性能评估。同时,为了得到更精确的结果,本实验进行100次10折交叉验证,最后对100次的结果求均值得到最终的结果。
4 分类特征评估
为了评估所选特征与分类器的关联性,研究中采用了最大相关最小冗余(minimum Redundancy MaximumRelevance,mRMR)算法[11]。此方法通过互信息来判断特征与类别之间的关联程度以及特征间的相似程度,以评估特征有效性。其中,MID指标代表最大相关与最小冗余的差,即信息差。R指标为判别性特征之间依赖性关系的一种描述,它要求每个判别性特征之间的相关性最小,即最小冗余原则。最大相关与最小冗余的术语表见表2。表2中:,表示两个变量的互信息;D表示判别性特征与类别之间的互信息值;h表示数据集的类别,l引表示判别性特征集的个数;R表示特征间的冗余性。研究中选择mRMR作为分类特征的评估方法是基于Matlab平台的mRMR工具包。
5 实验结果与分析
5.1 特征选择与分类结果
本实验使用重度抑郁症数据分别构建了5个节点规模的功能连接网络,并且将网络的度、中间中心度、节点效率三个局部属性定义为特征。对于不同的脑网络节点数量,将不同稀疏度下的局部属性使用AUC值统一后,分别得到的特征数量总数为270 (AAI90),768(Parc256),1 491 (Parc497),3 009 (Parc1003)和4 503(Parc1501)个。研究中,选择统计显著性P值作为特征选择方法,选择具有显著差异的局部拓扑属性作为判别性特征(P<0.05,FDR校验)。多节点规模下辨别性特征的数量与分类器的准确率,敏感性及特异性如表3所示。结果表明,随着网络节点数量的增多,每种局部属性的判别性特征的数目随之增加,而且分类器的分类准确率也呈上升趋势。表中:D(Degree)表示度;NE(NodeEfficiency)表示节点效率;BC( Beteenness Centrality)表示中间中心性。
5.2 P值特征选择方法
为了验证统计显著性P值作为5个模板的特征选择方法的表現,研究中对每个规模分别进行了特征的P值与MID值的关联分析。结果表明,所有规模中,P值与MID值二者均存在显著负相关,如图1所示。图1表明,利用统计显著性P值进行可判别性特征选择与机器学习方法同样有效,同时其并不受节点规模差异的影响。
此外,为了分析全部特征的分类表现,并发现最优特征子集,文中对所有特征按照P值进行排序,并以3为步长递增进行特征筛选,之后将所得特征用以训练分类模型。考虑到计算消耗,每个特征子集的分类重复5次。多个节点规模下不同特征数量对应的平均分类准确率如图2所示。结果表明,所有尺度均表现出类似的趋势。同时,随着初期特征数量的增加,分类准确率会持续上升。之后随着所增加的特征的有效性降低,分类准确率逐步下降。特别是,当把每个尺度的所有特征全部作为分类特征进行分类器构建时,准确率均为50%左右。
同时,5个尺度的分类结果均体现出传统方法中对P值的阈值设定0.05,并非最优值。图中虚线表示P=0.05时的特征数目对应的分类准确率,且分类准确率仍处于上升期。图中黑色最高准确率对应的特征数及近似P值分别为:39/0.162,111/0.119,204/0.115,324/0.096及654/0.126,这一结果暗示着,以P<0.05作为特征筛选的阈值过于严格,以致无法得到最高准确率。最优特征子集的构建是一个复杂的问题,这一问题涉及到特征数目、特征选择的方法、特征的有效性等方面。而特征数目对分类器性能,同样具有重要作用。从统计学角度,P<0.05的阈值设置能够充分保证所筛选的特征具有显著的统计学意义。但是,不得不说,这一设置从机器学习角度而言,显得过于严格,以至于所得到的特征较少,应该考虑更为宽松的阈值设置。
6结语
在机器学习方法中,研究分析了网络规模差异是如何影响分类准确率及特征选择策略。在利用P<0.05为特征选择策略时,研究发现更大的网络规模所带来的分类准确率是更高的。同时,研究中在不同节点尺度下传统的P值的特征选择方法均是可行的,这一假设得到验证。值得注意的是,P<0.05的阈值设置,能够充分保证所筛选的特征具有显著的统计学意义。但是,不得不说,這一设置从机器学习角度而言显得过于严格,以至于所得到的特征较少,应该考虑更为宽松的阈值设置。
参考文献
[1] GARETH B,LIBUSE P,ANDREW C,et al.Thalamocorticalconnectivity predicts cognition in children born preterm [J]. Ce-rebral cortex. 2015. 25: 4310-4318.
[2] HAN K,MAC DONALD C L,JOHNSON A M. et al.Disrupt-ed modular organization of resting-state cortical functional con-nectivity in U.S. military personnel following concussive' mild'blast - related traumatic brain injury [J]. Neuroimage. 2014,84:76-96.
[3] GARRISON K A. SCHEINOST D. FINN E S. et al. The sta-bility of functional brain network measures across thresholds[J]. Neuroimage , 2015 . 118 : 651-661.
[4]李越.郭浩,陈俊杰,等,抑郁症功能脑网络社团结构差异分析研究[J].计算机应与软件 , 2013( 7) : 52-56.
LI Yue. GUO Hao, CHEN Junjie, et al. Differences in associ-ation structure of functional brain network for depression [J].Computer application and software. 2013(7) : 52-56.
[5] JIE B, WEE C Y, SHEN D. et al. Hyper-connectivity of func-tional networks for brain disease diagnosis [J]. Medical imageanalysis, 2016, 32: 84.
[6] TEWARIE P. HILLEBRAND A, SCHOONHEIM M M. et al.Functional brain network analysis using minimum spanningtrees in multiple sclerosis : an MEG source - space study [J].Neurolmage, 2014( 88) : 308-318.
[7] JIE B, ZHANG D. GAO W, et al. Integration of network topo-Iogical and connectivity properties for neuroimaging classifica-tion [J]. IEEE transactions on biomedical engineering, 2014,61(2) : 576-589.
[8] JING B, LONG Z, LIU H, et al. ldentifying current and remit-ted major depressive disorder with the Hurst exponent : a com-parative study on two automated anatomical labeling atlases [J].Oncotarget, 2017( 8) : 904-912.
[9] OTA K, OISHl N. ITO K. et al. Effects of imaging modali-ties. brain atlases and feature selection on prediction of Al-zheimerWs disease [J]. Journal of neuroscience methods. 2015( 14 ) : 217-225.
[10] FEI Y, YUAN L X. FU S L. et al. An improved chaotic fruitfly optimization based on a mutation strategy for simultaneousfeature selection and parameter optimization for SVM and itsapplications [J]. PLOS ONE. 2017. 12(4) : 14-16.
[11] ZHANG N, ZHOU Y. HUANG T. et al. Discriminating be-tween lysine sumoylation and lysine acetylation using mRMRfeature selection and analysis [J]. PLOS ONE. 2014(9) : 142- 151.
作者简介:刘鸿丽(1992-),女,山西吕梁人,硕士,研究方向为人工智能、智能信息处理与脑影像学。

