基于GP-DINA模型的学生多级评分的广义认知诊断模型研究
王大洋 胡春红 卢秋婷

摘要:针对目前的多数认知诊断模型不能适用于多级评分的问题,文中基于GP-DINA模型,通过引入潜变量与滑动参数,提出一种面向学生的多级评分广义认知诊断模型。该模型将Q矩阵中的各属性设置为相等权重,并定义滑动矩阵导出相应的模型表达式。通过3 000名被试的35道题共15次循环模拟,发现该模型在线性型、无结构型、发散型、收敛型和独立型5种属性层级结构下均具有较高的模式准确率与边际判准率,能够为类似的认知诊断模型研究提供参考。
关键词:多级评分;认知诊断模型;GP-DINA模型;属性设置;滑动矩阵;模拟测试
中图分类号:TN911-34;TP393
文献标识码:A
文章编号:1004-373X( 2019) 24-0136-04
0 引言
现在广泛使用的传统测验,通常利用分数与排名反映学生的相对水平,但却忽视每个学生背后隐藏的技能、心理加工过程、策略等状况,不利于学生的自我认知及教育者对学生实际知识掌握情况的了解。因此,成为了针对性教学不可忽视的障碍[1-3]。近年来,认知诊断理论的出现,为个体加工技能、知识结构的测量和评价提供新的方法[4-5]。认知诊断理论有效结合现代测量学与认知心理学,其认知诊断测验可借助测试项目所对应的属性对被试者知识掌握程度进行有效反映[6]。
目前,使用较为广泛的认知诊断模型(基于IRT的心理测量学模型)主要有属性阶层模型、规则空间模型、DINA模型、NIDA模型等[7-10]。然而,这些模型只能提供0-1的评分,不能适用于多级评分的情况。因此,本文引入潜变量与滑动参数,基于GP-DINA模型提出一种面向学生的多级评分广义认知诊断模型。该模型将各属性设置为相等权重(1分),并定义可能滑动情况下的滑动矩阵,且给出模型表达式。借助35道题3 000名被试作答的模拟,以模式准确率与边际判准率(平均属性)为准确性指标,对该模型进行验证。验证结果表明,该模型效果良好,5种属性层级结构(线性型、无结构型、发散型、收敛型和独立型)均有较高的准确率。
1 DINA模型
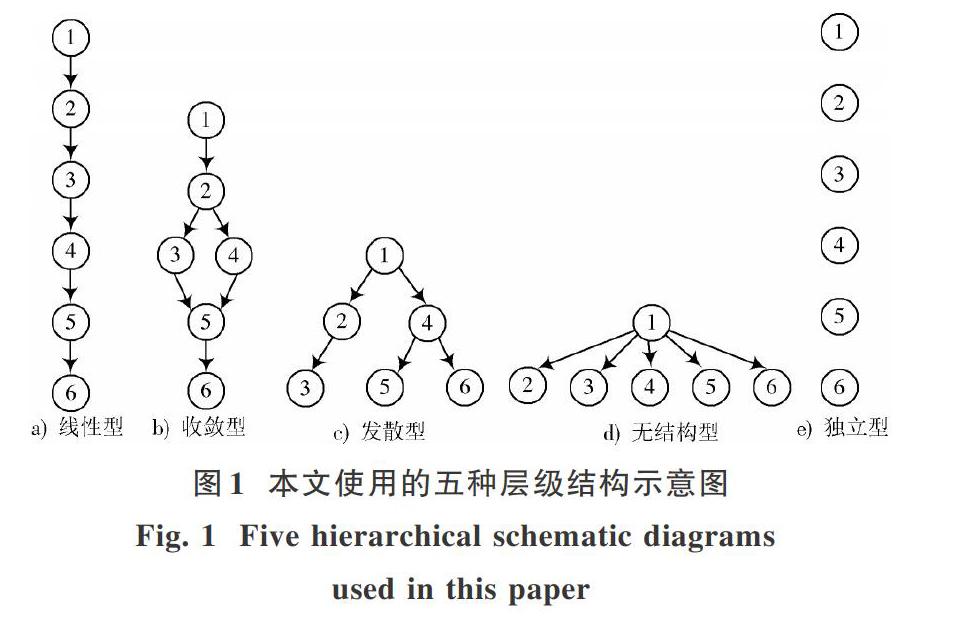
此外,本文采用5种类型的层级结构,分别为发散型、收敛型、无结构型、线性型和独立型,如图1所示,对该模型进行模拟。选题规则为:可达矩阵R必须能够保证被测验Qt矩阵包含;5种结构必须对相同数量的题目进行考查;对35道题(6分值2道、5分值4道、4分值5道、3分值6道、2分值8道、1分值10道)使用随机抽取的方式进行考查。对3 000个被试进行15次循环模拟,并假设各被试均采用理想反应模式作为其观测反应模式,具体过程如下:
1)根据总分情况,对理想反应模式(对应于可能掌握的知识状态)进行排序;按照概率(标准正态分布)分配人数,并使用平均分配的原则处理相同理想总分时的人数分配。
2)概率滑动顺次选取为0.06,0.12,0.24,0.36,分配
3)根据上述产生一随机数U,并与滑动概率矩阵(m=aiqj对应行的位置)概率值进行对比,完成观测反应模式数值的确定。
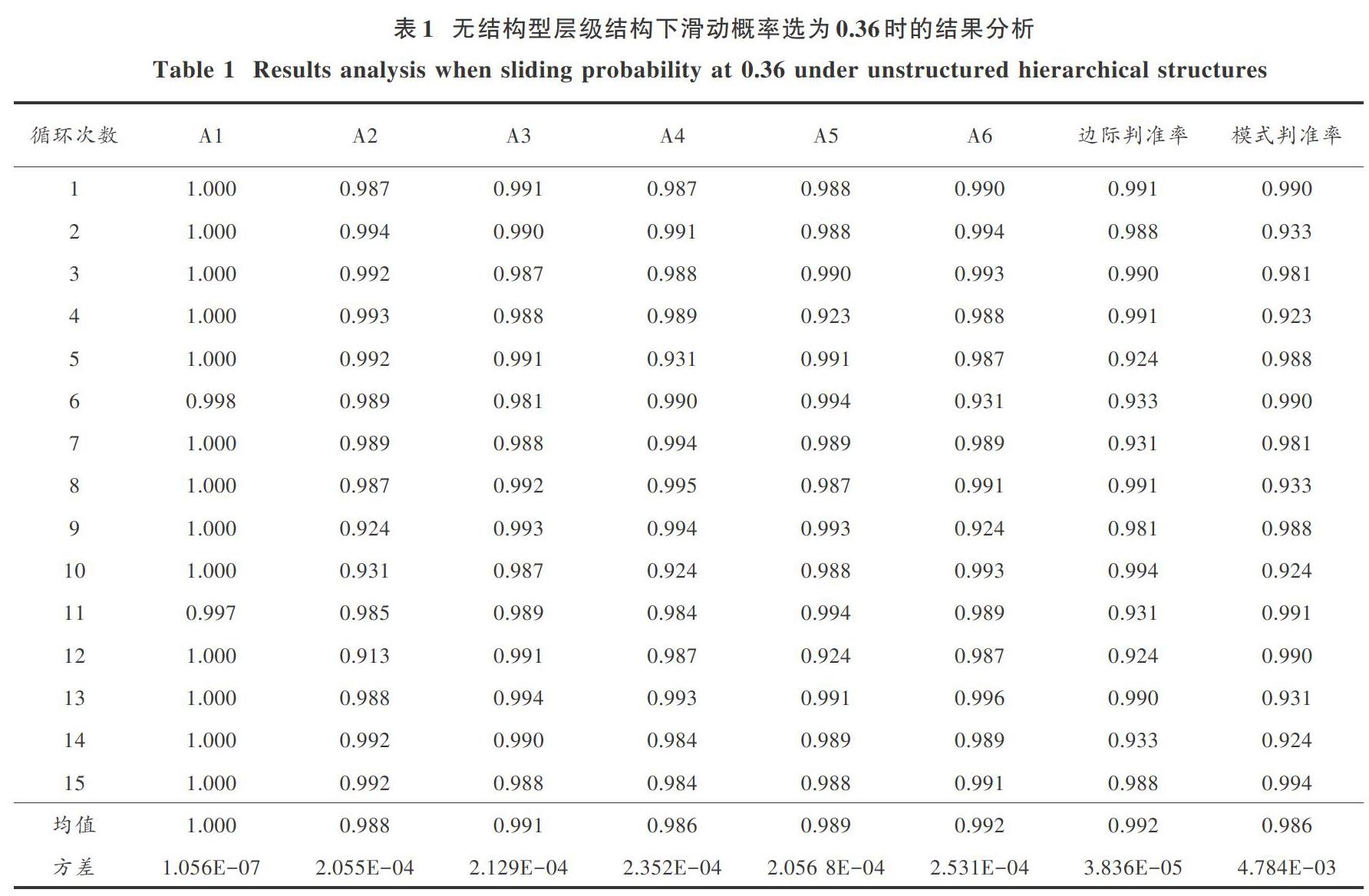
如表1所示,可知A1属性具有较高的属性判准率(大多等于1)与较小的方差。由于该属性为最高层级,被考查较多的次数;而其他属性则位于相等层次。因此,属性判准率均位于相似的水准(约为0.99),方差均处于10-4的量级。此外,还应注意到模式判准率(方差量级为10-3)低于边际判准率(方差量级为10-5),从而达到一般情况下的水准。
表2、表3分別为不同滑动概率下5种属性层级的属性边际判准率与模式判准率。从中得知,各层级的判准率在滑动概率为0.06时基本为同一水平。此外,各层级的判准率随滑动概率的增加而降低,其中,发散型、收敛型、无结构型和独立型的判准率降低速度会持续加快。
4 结语
通过引入多维潜变量与滑动矩阵,本文基于GP-DINA模型,提出一种多级评分广义认知诊断模型,可用于考查学生知识掌握的实际情况。该模型中属性权重相等,并借助定义的滑动矩阵推导出模型表达式。经过对3 000个被试的15次循环测试,发现该模型在5种属性层级结构(线性型、无结构型、发散型、收敛型和独立型)下均有较高的准确率,具有一定的使用价值。
参考文献
[1]单瑞婷,罗益承,孙翼.基于认知诊断的协同过滤试题推荐[J].计算机系统应用,2018( 24):136-142.
SHAN Ruiting, LUO Yicheng, SUN Yi. Collahorative filteringalgorithm based on cognitive diagnosis [J]. Computer systems&applications. 2018(24): 136-142.
[2]朱天宇,黄振亚,陈恩红,等.基于认知诊断的个性化试题推荐方法[J]计算机学报,2017(1):176-191.
ZHU TianVu. HUANG ZhenVa. CHEN Enhong, et al.Cogni-tive diagnosis based personalized question recommendation [J].Chinese journal of computers, 2017(1):176-191.
[3] TORRE J D L.A cognitive diagnosis model for cognitivelybased multiple -choice options [J]. Applied psychological mea-surement, 2009, 33(3):163-183.
[4] TORRE J D L,DOUGLAS J A.Model evaluation and multiplestrategies in cognitive diagnosis: an analysis of fraction subtrac-tion data[J1.Psychometrika. 2008, 73(4): 595-624.
[5] TORRE J D L,MINCHEN N.Cognitively diagnostic assess-ments and the cognitive diagnosis model framework [J]. Psico-logia educativa. 2014, 20(2): 89-97.
[6] TU D B, CAI Y, DAI H Q, et al.A polytomous cognitive diag-nosis model: P- DINA model [J]. Acta psychological sinica,2010. 42( 10): 1011-1020.
[7]郗闽.基于BN网络的学生广义认知诊断模型研究[J].现代电子技术,2018 .41( 24):79-81.
XI Min. Research on BN-based generlized cognitive diagnosismodel for students [J]. Modern electronics technique. 2018, 41(24):79-81.
[8]涂冬波,蔡艳,戴海琦.基于DINA模型的Q矩阵修正方法[J]心理学报,2012(4):558-568.
TU Dongbo, CAI Yan, DAI Haiqi.A new method of q-matrixvalidation based on DINA model [J]. Acta psychologica sinica,2012(4):558-568.
[9]王郁.基于HO-DINA模型的學生心理多级评分认知诊断模型研究[J].现代电子技术,2018 ,41(2):53-55.
WANG Yu. Research on multi-level scoring cognitive diagnosismodel for students' psychology based on HO-DINA model [J].Modern electronics technique, 2018, 41(2):53-55.
[10]刘彦楼,辛涛,田伟,项目反应理论与认知诊断模型的参数估计:模型整合视角[J]北京师范大学学报(自然科学版),2017.53(6):742-748.
LIU Yanlou. XIN Tao. TIAN Wei. Estimation of parametersof item response theory and cognitive diagnosis model: modelintegration perspective [J]. Journal of Beijing Normal Universi-tv( Natural science edition), 2017, 53(6):742-748.
[11]张静,张兆基,周佐.EM算法在状态空间模型参数辨识中的应用[J].控制T程.2018 .25(7):1348-1354.
ZHANG Jin. ZHANG Zhaoji, ZHOU Zuo. Application of EMalgorithm in parameter identification of state-space model [J].ontrol engineering of China, 2018. 25(7): 1348-1354.
作者简介:王大洋(1985-),男,满族,吉林四平人,硕士,讲师,研究方向为现代教育信息化、创新创业教育、学生教育管理。

