铀氢化反应过程中氢扩散行为的第一性原理研究

宾 韧， 王 鑫， 敖冰云， 汪小琳

( 1.表面物理与化学重点实验室，江油 621908； 2.中国工程物理研究院材料研究所，江油 621907； 3. 中国工程物理研究院，绵阳621900 )

1 引 言

铀的氢化腐蚀以其快速反应和对材料的显著破坏而备受研究者们关注. 而极高的化学活性使得金属铀表面不可避免存在由氧化物及吸附杂质构成的表面层，从而导致了铀氢化反应行为非常复杂. 表面层的状态如氧化层厚度及特性、表面吸附杂质种类和浓度、表面粗糙度、机械加工导致的残余应力等，都影响着氢化反应的成核机制及动力学特征[1].

铀氢化反应可分为四个阶段：(1)孕育期. 其主要原因是反应初期氢需扩散通过表面层，在界面处累积到临界浓度才能生成氢化物. 氧化层的厚度决定了氢在其中扩散到达界面并达到足够浓度所需要的时间[2]. (2)线性生长阶段. 孕育期结束后，氢化物发生局部形核并开始生长. 这一阶段由于表面层及金属基体的不均匀性，氢化物形核位点具有离散且分布不均匀的特性[3]. 但单个氢化物核的尺寸增长速率近似为线性，而整体氢化反应速率曲线呈S型. (3)体相反应阶段. 这一阶段各氢化物形核点相互连接并完全覆盖金属表面，这也意味着表面氧化层的完全破坏. 此时反应速率达到最大值且近似不变，反应由氢化物-金属界面的性质控制[4]. (4)终止阶段. 这一阶段反应物耗尽，反应速率逐渐降低直至终止.

从微观上看，在铀氢化反应过程中涉及的介质及其主要作用有：

(1)铀氧化物. 研究表明，UO2表面氢分子吸附的粘滞系数约6×10-4，氢原子在UO2晶格中溶解度仅为7×103cm-3，而扩散势垒达57-60 kJ·mol-1[5, 6]，这使其在氢化反应过程中起到扩散阻挡层的作用，其厚度影响孕育期和初期成核速率[7].

(2)金属铀. U与H2的反应在能量上是有利的，因此反应速率主要由动力学因素决定. 氢在U晶格中的饱和溶解度仅为5×1017cm-3[8]，远小于生成氢化物所需的临界氢浓度(1.4×1023cm-3)，这导致氢不可能在铀表面均匀反应，而是在晶界、第二相界面等处优先聚集到足够浓度才能形核[9, 10].

(3)铀氢化物. 在氢化反应的体相阶段，反应生成的UH3成为阻隔H2与金属基体的唯一介质. 但与氧化物不同的是，疏松的UH3不仅不能阻止反应，反而对氢化反应起到促进作用，反应速率在体相阶段达到最大值. 目前氢在UH3晶格中的溶解与扩散行为仍没有定量研究数据.

为研究铀的氢化反应动力学及产物特性，笔者在其表面沉积一层相对惰性的金属Pd，以促进氢的解离吸附、阻挡表面生成氧化层并降低杂质气体的吸附，因此铀的氢化反应不存在孕育期. Pd对H2具有较高的选择透过性，且其氢化物PdHx(x=0.6～0.7)中氢原子密度达43 nm-3，更易达到β-UH3的成核的临界氢浓度(82 nm-3)，因此氢化反应后在Pd膜下生成了厚达数个微米的均匀层状α-UH3.α-UH3只能在低温、低压、惰性气体稀释下缓慢反应生成[11-13]，而通常条件下铀氢反应产物几乎全部为β-UH3. 在沉积Pd的条件下，反应初期氢化速率在较长时间内保持恒定；而在反应后期Pd膜破裂后氢化反应速率明显上升. 这表明与通常氢化反应体相阶段相比，Pd膜的存在导致氢化反应的速率受到了限制，导致反应产物主要为α-UH3.α-UH3被认为是亚稳态，或者氢化反应过渡产物，长时间加热将不可逆地转化成β-UH3. 事实上，α-UH3与β-UH3具有相似的结构和密度，两者的形成能非常接近[14]，实验测得的生成焓差异小于量热装置的误差[15]. 因此铀氢化反应产物的选择性，主要由动力学因素控制，即主要涉及氢在上述介质中溶解、扩散过程.

然而，对铀氢化反应动力学特性及产物选择性的研究，难以在实验上深入到微观层次. 这是因为铀及其氢化反应产物均具有非常高的化学活性，在制备和分析过程中会发生严重的氧化；通过实验制备的α-UH3不可避免地混有大量的β-UH3，且无法有效的分离，也对α-UH3相关性质的实验研究带来困难. 采用理论计算可以模拟微观尺度上氢化反应的发生过程，是对实验研究的有力补充. 但以往对U-H体系的理论研究报道多以氢化物基态性质和氢原子的静态性质为主[16-18]，缺乏动力学相关的详细报道，因此，本文利用第一性原理计算方法，尝试从微观上分析氢在UO2、PdHx及两种氢化产物α-UH3、β-UH3中固溶、扩散的行为，来研究不同表面状态下氢化反应动力学特性，以期解释Pd膜作用下氢化反应产物具有选择性的原因.

2 计算方法和模型

本文用于实现密度泛函计算的程序为VASP (Vienna Ab-initio Simulation Package)[19]，采用基于广义梯度近似 (GGA)的Perdew-Burke-Ernzerhof泛函[20]，所选取的赝势也对应为采用投影缀加平面波方法构建的PAW-PBE赝势，涉及元素选用的价电子态为U 5f36s26p66d17s2，Pd 4s24p64d10，O 2s22p4，H 1s1. 经收敛性测试，截断能统一设定为600 eV，并采用足够的k网格密度(0.05 Å-1)以保证能量收敛到10-5eV. 在晶体结构弛豫方面采用精度逐渐提高的分步优化方法，即先采用共轭梯度(CG)方法对晶格进行初步优化，再用精度更高的拟牛顿(RMM-DIIS)方法进行进一步的结构优化，直到所有原子的受力收敛到0.001 eV/Å-1，然后采用Blöch修正的四面体方法进行静态计算. 考虑到U-H体系具有磁性，在计算时考虑自旋极化，并确定α-UH3和β-UH3的基态磁性质.

对氢原子在材料中的扩散路径和扩散势垒的相关计算是利用Henkelman小组开发的VTST(Transition State Tools for VASP)程序包提供的CI-NEB(Climbing image nudged elastic band)方法来实现. 它通过确定两个能量最低的掺杂构型作为初态或终态(可能是能量相同的等效构型)，设计可能的扩散路径，再使用CI-NEB方法计算扩散路径中原子逐渐运动的一系列构型的能量、受力情况，所获得能量最高的点确定为扩散路径中的过渡态. 弛豫后得到的一系列中间构型即为扩散过程中的最小能量路径(minimum energy path, MEP)，过渡态与基态(初始态或终态)之间的能量差即为扩散势垒. 由于掺杂构型的体系较大且对称性较差，对扩散路径中各镜像的计算精度稍有降低(k点网格密度0.1 Å-1，受力收敛到0.01 eV/ A-1). 获得鞍点构型后，为了进一步提高过渡态的结构和能量精度，再利用Dimer方法在该构型附近进行更精细的过渡态结构搜索[21, 22]. 另外，对原子构型文件的编辑处理及相关图像绘制均利用免费软件VESTA[23]完成并输出.

3 结果及讨论

3.1 氢化物晶体结构

α-UH3和β-UH3均具有Pm-3m(223)的空间构型，但两者的原子占位不同. 两种氢化物的晶体构型如图1所示. 在α-UH3单胞中有两个U原子和6个H原子，分别占据Wyckoff 2(a) (0, 0, 0)和6(d) (1/4, 0, 1/2)位置；而在β-UH3单胞中，8个U原子分为两组(UI和UII，如图1b所示)，分别占据了2(a)和6(d)的格点(对应α-UH3中U、H原子的位置)，而24个氢原子占据了24(k) (0, 0.156, 0.313)位置[24]. 可以看出，α相和β相中，所有U原子均处于12个氢原子组成的二十面体笼中，U-H距离均为2.31 Å[25].

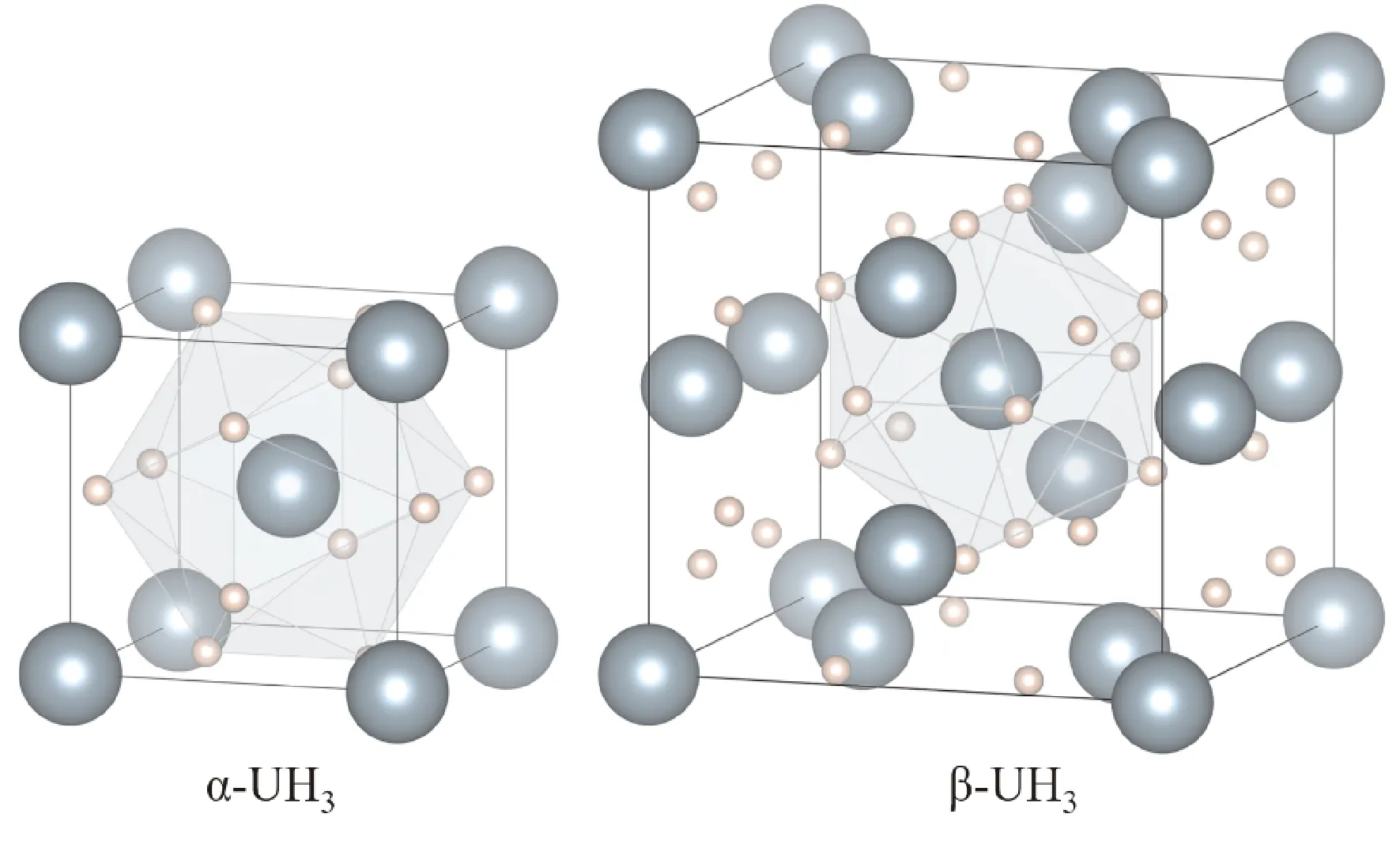
图1 α-UH3和β-UH3的晶体结构Fig. 1 Crystal lattice structures of α-UH3 and β-UH3

3.2 两种氢化物形成能的计算

衡量通常状态下两种氢化物相之间稳定性差异，最直接的方法是比较两者的形成能ΔEf(Energy of Formation)，对氢化反应

(1)

定义UH3的形成能ΔEf

(2)

即生成物总能减去生成该物质所需的反应物总能之和. 与镧系元素类似[26, 27]，在计算时也要考虑磁性的贡献. 表1列出了计算得到的α-UH3、β-UH3的晶格常数和形成能，作为对比还计算了α-U的晶格常数、UO2的晶格常数及形成能，并与实验值对照.

表1α-U、α-UH3、β-UH3和UO2等物质的晶格常数及形成能

Table 1 Calculatedand experimental lattice constants and energy of formation forα-U,α-UH3,β-UH3and UO2

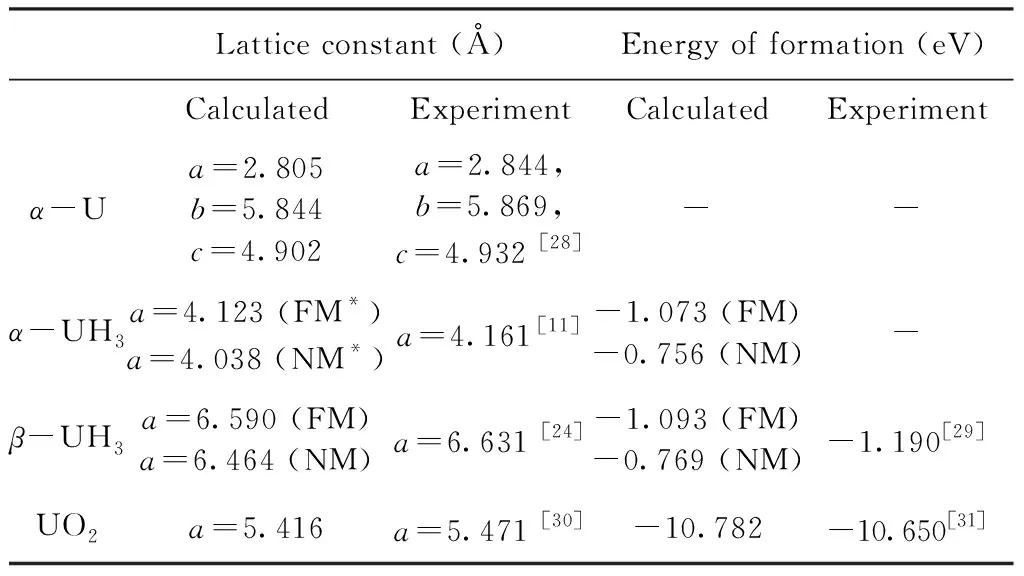
Lattice constant (Å)Energy of formation (eV)CalculatedExperimentCalculatedExperimentα-Ua=2.805b=5.844c=4.902a=2.844,b=5.869,c=4.932 [28]--α-UH3a=4.123 (FM*)a=4.038 (NM*)a=4.161[11]-1.073 (FM)-0.756 (NM)-β-UH3a=6.590 (FM)a=6.464 (NM)a=6.631 [24]-1.093 (FM)-0.769 (NM)-1.190[29]UO2a=5.416a=5.471 [30]-10.782-10.650[31]

*FM：ferromagnetic，NM：non-magnetic

由表1可以看出，考虑了自旋极化后，α-UH3、β-UH3的基态均具有铁磁性，其晶格常数、形成能的计算值与实验值均符合较好. 虽然α-UH3的生成焓略高于β-UH3，被认为是亚稳态，但计算结果表明它们之间生成焓的差异非常小，只有0.020 eV/atom U (2.03 kJ·mol-1). 单纯从热力学稳定性差异来解释α-UH3产量远少于β-UH3这一现象并不充分. 下面我们建立氢原子在α-UH3、β-UH3、UO2和PdHx中掺杂的模型，比较不同浓度下掺杂的溶解能，并计算掺杂原子在间隙中扩散的势垒.

3.3 掺杂体系的溶解能

氢原子自身体积非常小，在晶格中一般以填隙固溶的方式存在，对晶格中所填充的间隙位而言，它的优先占据首先必须考虑间隙的大小. 由于α-UH3和β-UH3晶格中的铀原子均与最近邻的氢原子构成了UH12正二十面体，氢原子较易进入这些正二十面体之间的间隙. 如图2所示，这样的间隙一共有三种，分别为α-UH3(0, 1/4, 1/2)、β-UH3(0, 1/4, 1/2)和β-UH3(1/4, 1/4, 1/4)，这些间隙均由氢原子构成，间隙内氢原子并不会与铀原子直接接触.

图2 氢化物晶格中的几种间隙Fig. 2 Interstitials in α-UH3 and β-UH3 lattices

不考虑掺入氢原子后引起的晶格畸变，这些间隙中心与最近邻的氢原子之间的距离分别为1.47 Å、1.39 Å、1.82Å，均显著大于氢原子半径，这表明这些间隙可能具有容纳多个氢原子的能力. 近期研究者们通过理论和实验研究发现，类似LaH10[32]，在加压的情况下铀与氢可形成一系列的化合物且可能具有超导特性[33, 34].

不考虑温度和压力条件，氢化物中氢原子的溶解能为

(3)

其中Eintrinsic和Edoped为掺杂前后氢化物晶胞的能量(均充分弛豫)，EH2为孤立氢分子能量，n为晶格中掺入的H原子数目，m为所计算晶胞中U的数量. 为得出溶解能随掺杂浓度的变化趋势，选取α-UH3的2×2×1超晶胞及β-UH3单胞，依次向对应间隙填充氢原子，对这些掺杂构型进行计算得出该间隙氢的溶解能. 为使掺杂体系能量最低，插入的氢原子两两之间尽可能远、且对称性尽可能高. 计算结果如图3所示. 作为对比图中也给出了UO2晶格中氢原子的溶解能变化.

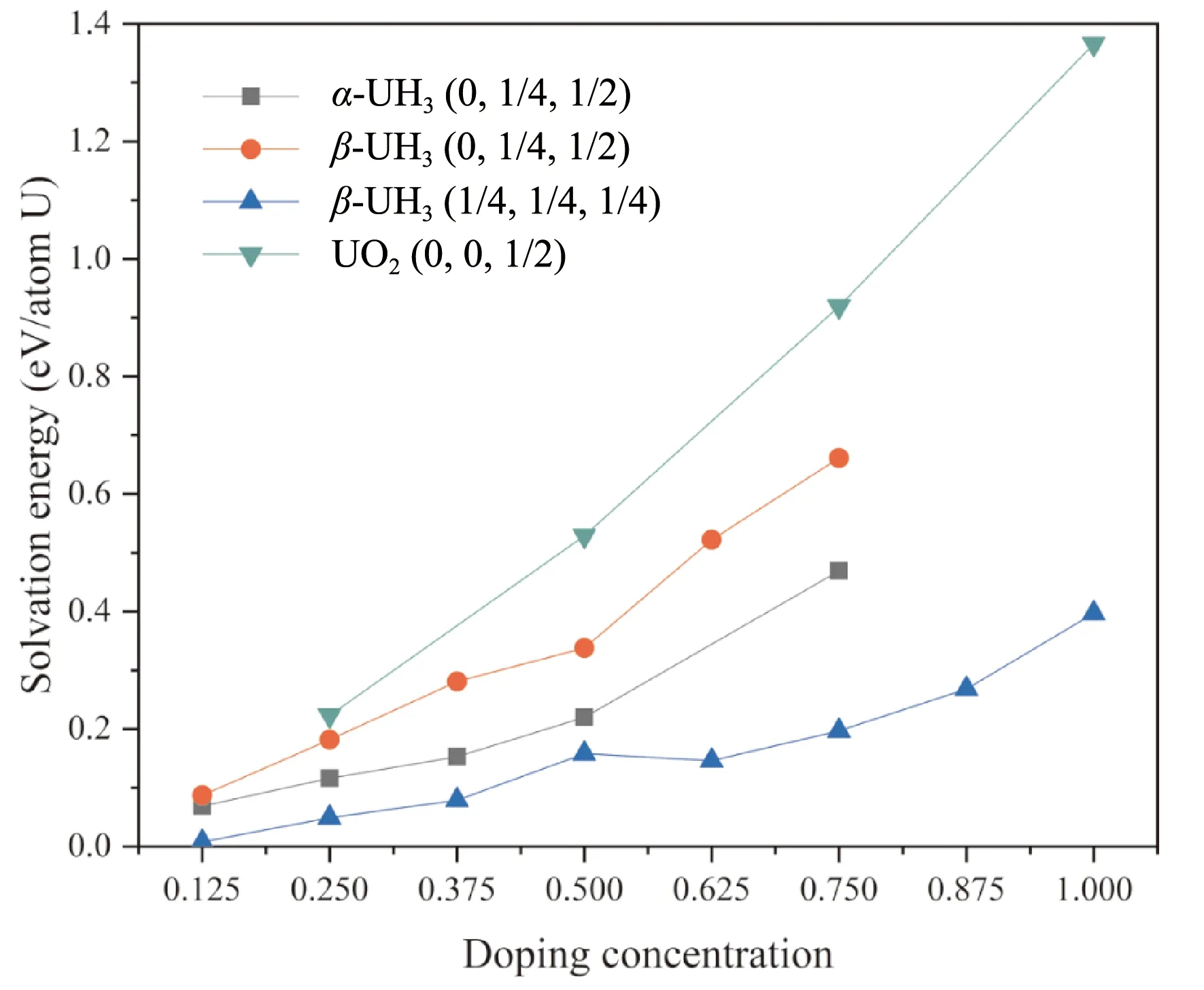
图3 α-UH3(0, 1/4, 1/2)、β- UH3(0, 1/4, 1/2)、β- UH3(1/4, 1/4, 1/4) 及UO2(0, 0, 1/2)三种间隙氢原子溶解能随掺杂浓度的变化Fig. 3 Energies for H dissolved in α-UH3(0, 1/4, 1/2), β- UH3(0, 1/4, 1/2), β- UH3(1/4, 1/4, 1/4) and UO2(0, 0, 1/2) interstitials as a function of doping concentration

在间隙插入H原子后，UO2晶格中的八面体间隙(0, 0, 1/2)掺杂氢原子后能量显著升高，这与UO2中氢溶解度极低的实验结论相符. 两种氢化物晶格的氢溶解能及其升高的幅度均较小，其大小关系为β-UH3(0, 1/4, 1/2) >α-UH3(0, 1/4, 1/2) >β-UH3(1/4, 1/4, 1/4)，这说明较大的间隙掺入氢原子后发生的畸变较小，因而氢溶解能及其随掺杂浓度的升高幅度较小. 比其他两种间隙小一个量级. 在掺杂浓度较小时，体系的溶解能近似呈线性上升，表明距离较远的间隙可近似视为孤立，这些位置上掺杂基本互不影响. 更高的掺杂浓度溶解能的变化偏离线性，且往往是正偏离，表明掺杂H原子之间的相互作用使得体系的能量上升.

β-UH3单胞中(1/4, 1/4, 1/4)间隙位掺杂一个氢原子的的溶解能仅为0.008 eV，而α-UH3(0, 1/4, 1/2)间隙掺杂一个氢原子的溶解能为0.069 eV，为两种晶格中溶解氢原子的优先位点，因此下文主要就这两种间隙位的氢原子扩散扩散讨论.

3.4 氢在几种介质中的扩散势垒

根据扩散Arrhenius方程

(4)

不考虑指前因子差异的情况下，具有更低迁移势垒的晶格中氢的扩散速率更高，因此扩散势垒可以在一定程度上体现氢在材料中扩散速率的快慢. 为对比氢原子在氢化反应过程中可能涉及的介质中的扩散特性，下面计算H原子在α-UH3(0, 1/4, 1/2)间隙、β-UH3(1/4, 1/4, 1/4)间隙、UO2(0, 0, 1/2)间隙及PdHx(0, 0, 1/2)间隙中扩散的最小能量路径，及对应的扩散势垒.

3.4.1α-UH3(0,1/4,1/2)间隙

由于氢原子半径较小，它在晶格中的扩散往往通过格点原子的间隙进行. 但完整无缺陷的晶格中氢原子的扩散较难，因为它会导致晶格原子发生较大畸变，使得扩散过程的势垒较高. 图4是α-UH3中氢原子沿(0, 1/4, 1/2)间隙直接扩散的最小能量路径，可以看出其扩散势垒高达1.04 eV，表明氢原子采取这种方式进行扩散的概率较小.

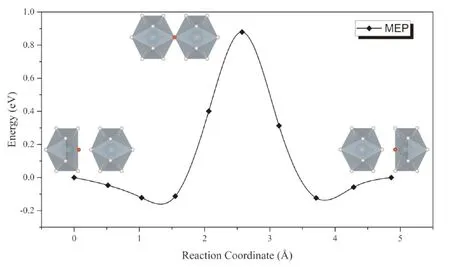
图4 间隙H原子在α-UH3直接扩散的MEP曲线Fig. 4 The minimum energy path for direct diffusion of H atoms between α-UH3 interstitials

考虑到α-UH3中存在大量格点氢原子，且U原子对周围的H原子接近于金属氢中的弱陷获作用，格点处的氢原子较容易脱离平衡位置发生迁移. 因此，可以假设处于间隙的氢原子与格点上氢原子之间发生协同扩散，即位于间隙处的氢原子向扩散路径上的格点位移动，而原先位于格点处的氢原子同时向下一个平衡间隙位置移动. 在这种扩散模式下，除了扩散原子与协同扩散的原子外，其他原子发生的原子位移很小，因而扩散势垒与直接扩散相比有显著的降低.α-UH3中H通过协同扩散进行迁移的反应路径如图5所示. 可以看到，最小能量路径呈现出周期性起伏，势垒仅为0.16 eV.

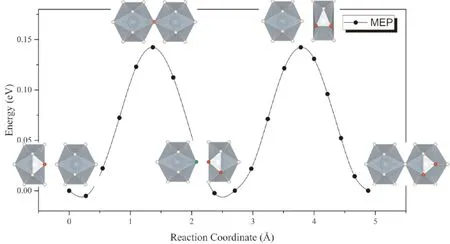
图5 H原子在α-UH3中通过格点原子H协同扩散的MEP曲线Fig. 5 The MEP of interstitial H diffusion in α-UH3 lattice with the cooperation of H in lattice position

3.4.2β-UH3(1/4,1/4,1/4)间隙

同样考虑上述两种扩散模式，一种是位于间隙的氢原子直接向相邻同种间隙扩散，可以看到扩散过程种附近的UH12正二十面体发生较大畸变，因而势垒同样高达0.93 eV (图6)，表明按照此种方式进行扩散的速率非常低，这一点与通过α-UH3间隙扩散的情形相似. 而考虑间隙处的氢原子与UH12正二十面体中的一个氢原子协同扩散的话，扩散势垒大幅降低到了0.09 eV (图7).

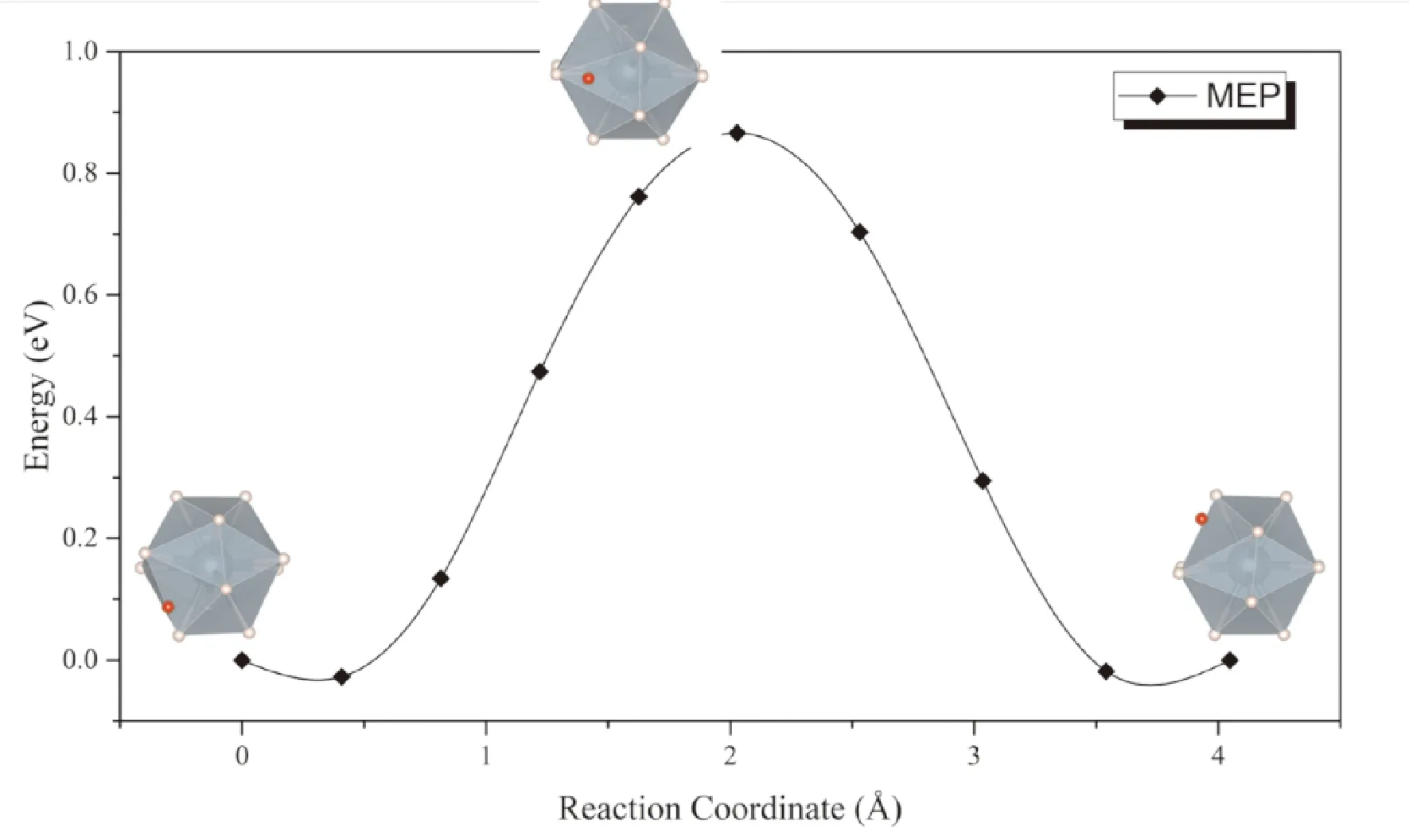
图6 H原子通过β-UH3间隙扩散的MEP曲线Fig. 6 The MEP for direct diffusion of interstitial H in β-UH3

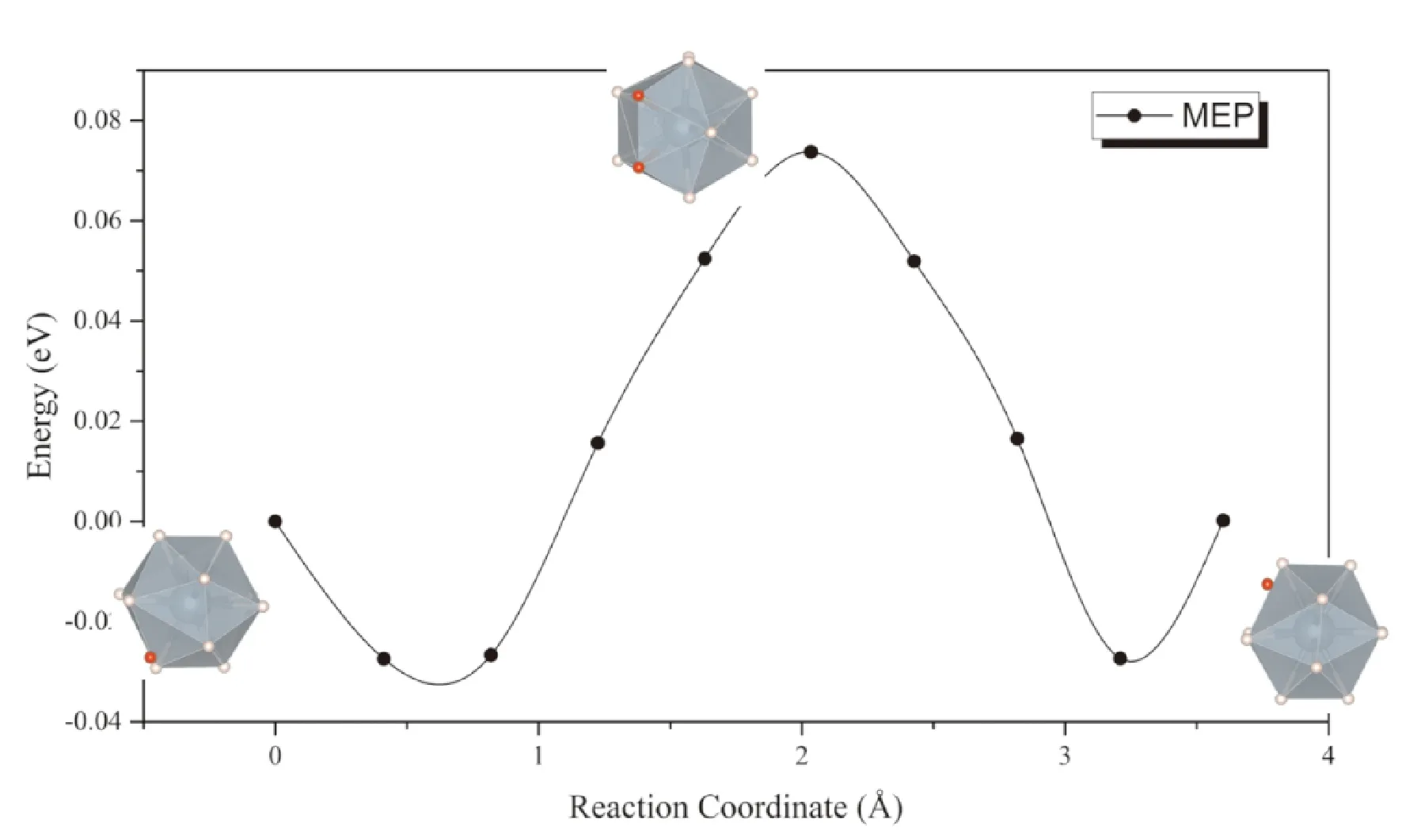
图7 H原子在β-UH3中通过格点原子协同扩散的MEP曲线Fig. 7 The MEP of interstitial H diffusion in β-UH3 lattice with the cooperation of H in lattice position

由于氢原子的溶解能较低，在与α-UH3密度相近的情况下，β-UH3中氢的溶解度比α-UH3要高. 而从图7可以看出，同样是在二十面体上的格点氢原子协同下，氢在β-UH3中扩散的势垒也显著低于其在α-UH3中扩散的势垒. 因此，氢通过β-UH3进行扩散的速率，将显著高于其通过α-UH3扩散的速率.

3.4.3UO2(0,0,1/2)间隙

对扩散势垒的计算主要考虑H原子在相邻八面体间隙之间扩散的情形. 从图8中可以看出，扩散过程中能量鞍点的构型为氢原子位于两个O原子中间，三者在一条直线上的情形. 计算结果表明H原子在UO2晶格中的扩散势垒的计算值为213 kJ·mol-1(2.20 eV)，显著高于57-60 kJ·mol-1的实验值. 这表明H原子通过铀氧化物的扩散主要通过间隙、晶界等氧化层内的缺陷进行扩散，而在完整晶格中的扩散几乎可以忽略.

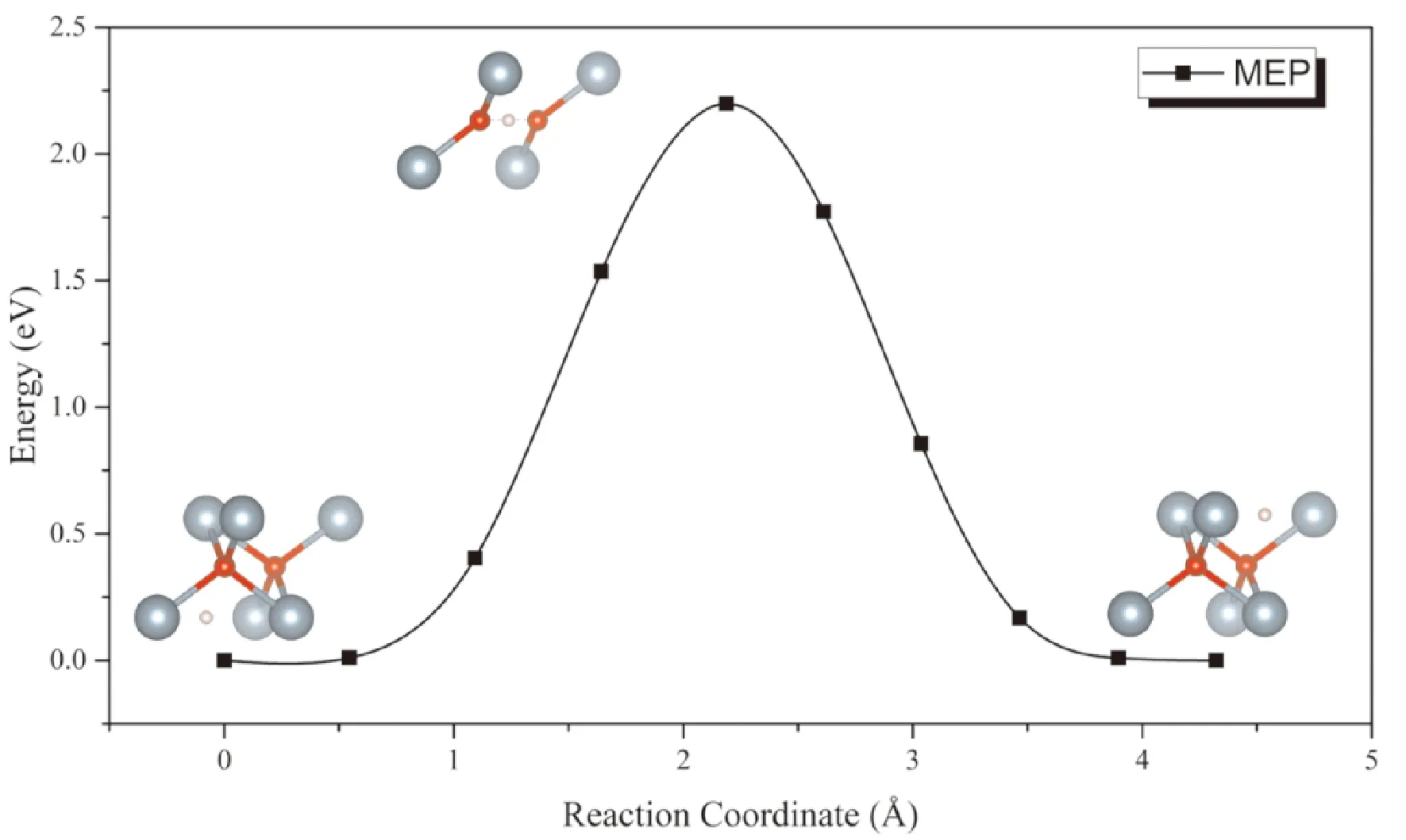
图8 H原子在UO2间隙通过扩散的MEP曲线Fig. 8 The MEP of H diffusion in UO2 interstitials

3.4.4PdH0.5(0,0,1/2)间隙

依据文献报道[35]，PdHx晶格中H占据Pd晶格的八面体间隙，形成NaCl型晶体结构. PdHx晶格中氢原子含量升高，Pd的面心立方骨架结构不变，氢原子随机填充剩余八面体间隙，导致其晶格发生一定膨胀. 为了简化讨论，选取PdH0.75的本征原子配比，其中H原子分别占据Pd晶格的三个八面体间隙位，考虑其中一个掺杂H原子向邻近间隙移动的扩散模型.

由于PdH0.5晶格中仅有一半的八面体间隙被H原子随机占据，H原子可以在相邻的间隙之间迅速迁移. 从图9中可以看出，扩散过程中能量鞍点的构型为氢原子位于Pd组成的八面体笼的一条棱的中点(即相邻的四面体间隙位)，此时体系能量较低，但在这种过渡态构型下Pd原子骨架仍发生了一定的变形，这导致H原子在PdH0.5晶格中扩散的势垒为0.19 eV，略高于H原子在α-UH3中的扩散势垒.

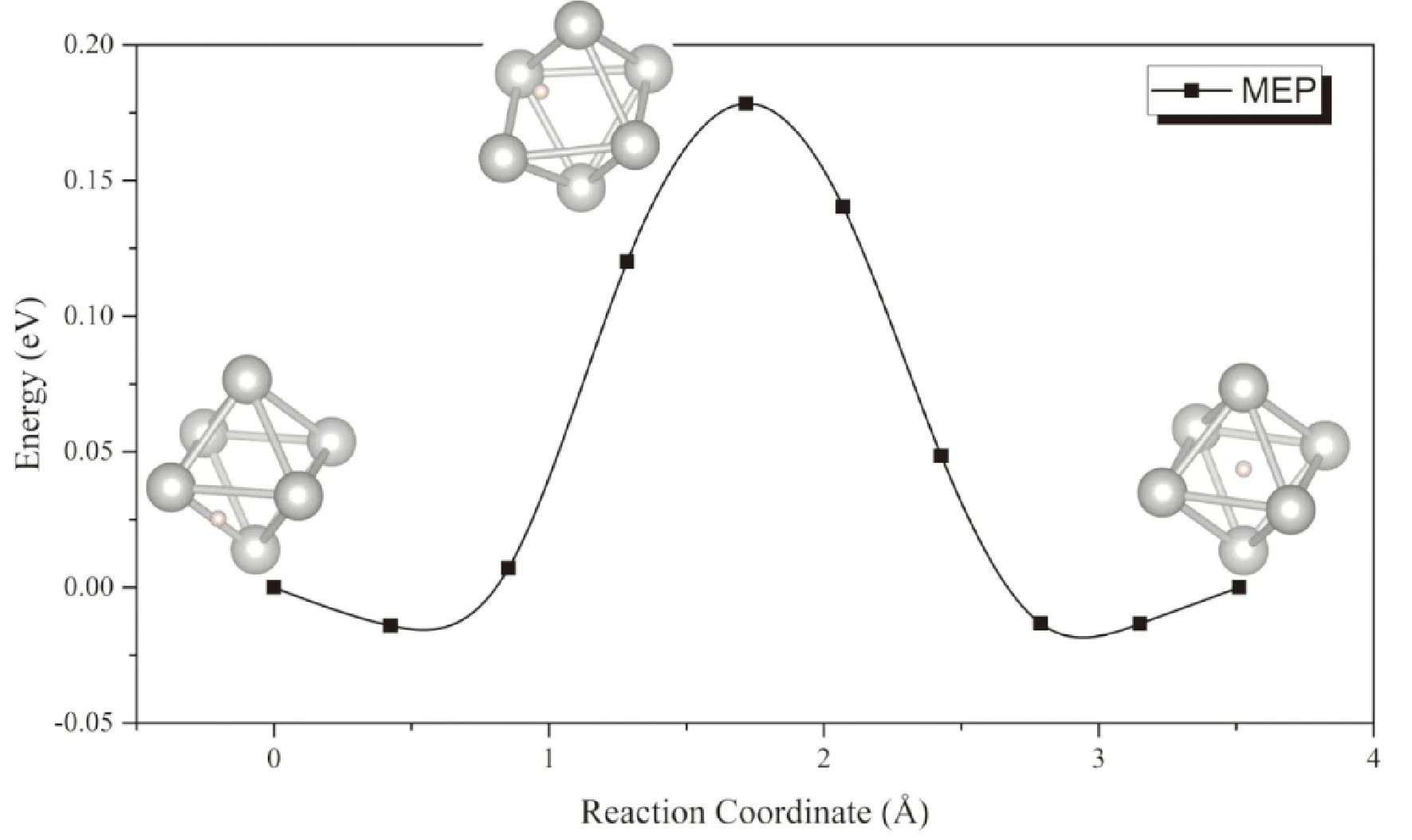
图9 PdH0.75中氢原子在Pd晶格八面体间隙移动的MEP曲线Fig. 9 The MEP of the migration of H atom between octahedral interstitials in PdH0.75

3.5 几种介质中氢扩散势垒的讨论

α-UH3、β-UH3、UO2、PdHx四种介质中H的掺杂溶解能和扩散势垒如表2所示.

表2 四种介质中氢掺杂的溶解能和扩散势垒

Table 2 Energy of dissolution and diffusion barriers of H atoms in four mediums

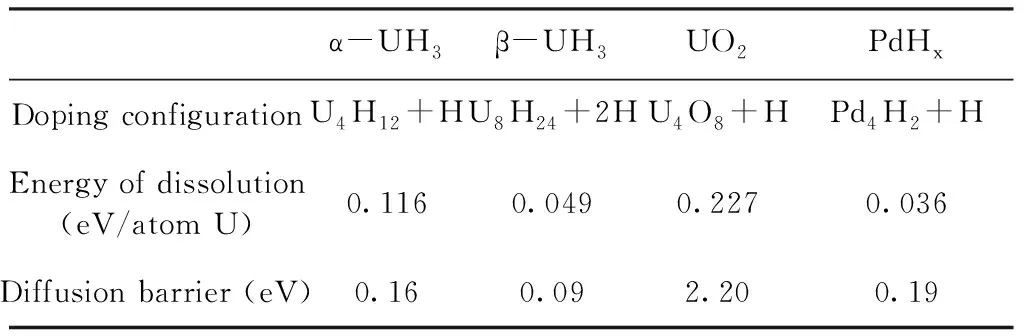
α-UH3β-UH3UO2PdHxDoping configurationU4H12+HU8H24+2HU4O8+HPd4H2+HEnergy of dissolution(eV/atom U)0.1160.0490.2270.036Diffusion barrier (eV)0.160.092.200.19

由上面的分析可以看出，无论是α-UH3还是β-UH3中，氢原子单独在间隙中进行扩散的势垒非常大，接近1 eV；而通过格点处氢原子协同进行扩散，其势垒则非常小，分别为0.16 eV (15.5 kJ·mol-1)和0.09 eV (8.7 kJ·mol-1)，甚至可以借助热运动进行扩散. 同时由于铀氢反应为放热反应，因此氢的扩散不会成为反应的速率控制步骤. 而氢在α-UH3晶格中引发的溶解能比β-UH3中大，且扩散势垒也相对较高，因此氢在α-UH3晶格中的扩散速率相对较低.

考虑到氢在氢化物表面可以自发解离，可以预计，一旦氢气与铀氢化物直接接触，尤其是与溶解度和扩散速率均较高的β-UH3直接接触，将很快解离成氢原子并扩散通过氢化物层到达反应界面，加上β-UH3具有超高的比表面积[36, 37]，这也是氢化物具有自催化效应的原因. 向铀表面沉积一层金属Pd膜，一方面可以通过限制到达反应界面的氢通量来降低反应速率，使产物中α-UH3的比例升高，另一方面可以限制β-UH3与氢的接触，从而抑制β-UH3的生成.

4 结 论

第一性原理计算结果表明，固溶氢原子在α-UH3和β-UH3中能量最低的间隙位分别为(0, 1/2, 1/4)和(1/4, 1/4, 1/4)，且低浓度下氢原子溶解能随掺杂浓度近似线性增加. 氢在UO2中具有非常大的扩散势垒(2.2 eV)，表明完整UO2晶格中氢的扩散非常困难，使得氢的扩散需通过空位等缺陷进行. 在α-UH3和β-UH3中，间隙氢原子可通过格点氢原子进行协同扩散，使得它们具有非常低的扩散势垒，但α-UH3中扩散势垒(0.16 eV)高于β-UH3中的扩散势垒(0.09 eV)，对应着较低的氢化反应速率. Pd层中氢的扩散势垒为0.19 eV明显高于β-UH3而与α-UH3相近，表明Pd膜覆盖的情况下，其反应速率与表面生成α-UH3的情形相近，这可以部分解释Pd膜覆盖下铀氢化反应主要产物为α-UH3的现象.