基于机器视觉的量子点STM形貌图像识别研究

唐泽恬， 杨 晨， 汤佳伟， 夏成蹊， 曾瑞敏， 余圣新， 罗子江， 丁 召

(1. 贵州大学大数据与信息工程学院 贵州省微纳电子与软件技术重点实验室，贵阳 550025; 2. 贵州财经大学信息学院，贵阳 550025)

1 引 言

机器视觉技术是通过图像处理技术进行图像分析或控制装置完成预设操作的一种非接触式测量技术, 可以对目标物体的外形特征、位移尺寸等几何量进行实时检测[1]. 低维材料通指材料的线度比电子的德布罗意波长或电子的平均自由程短 (或相当)的材料[2]. 其中半导体量子点器件具有特殊的光学性质，被广泛应用于红外探测和光伏电池领域[3-5]. 斜切衬底的方向，量子点的密度、尺寸和均匀性对量子点器件的性能有重要影响[6, 7]. 因此对低维半导体的衬底和量子点的形貌特征研究有着重要意义. 而利用机器视觉的方法可提高低维半导体表面形貌研究的效率和精度.

目前，在低维半导体表面形貌研究的过程中，原子力显微镜(Atomic Force Microscope，AFM)和扫描隧道显微镜(Scanning Tunnel Microscope ,STM)为常见的表面形貌表征手段[8, 9]，分析过程需要一定的人工参与. 相比之下基于机器视觉的方法具有较高的精度和效率. 机器视觉在半导体方面有所发展，巢渊等[10]将机器视觉应用于半导体表面缺陷的在线检测；杜俊斌等[11]利用机器视觉构建了废旧半导体自动分选硬件系统；许龙等[12]利用机器视觉实现了SOP双排式芯片的管脚识别定位和外观尺寸检测.

机器视觉在半导体方面的研究主要集中在器件的自动识别，半导体芯片表面图像检测等领域. 在低维半导体衬底和量子点形貌特征领域方面，此类研究尚不多见. 因此本文基于机器视觉对衬底和量子点的STM图像进行检测，利用图像腐蚀、边缘检测、二值化和阈值下降等方法使衬底斜切角、量子点数量、均匀性及尺寸等参数的统计更加高效.

2 系统结构

如图1所示是基于机器视觉的衬底和量子点形貌特征分析STM图像的系统框图. 系统对衬底和量子点的形貌特征进行研究，系统可分为两部分，第一，对衬底图像进行腐蚀、台阶提取和斜切角计算，得出斜切角大小；第二，对量子点图像，进行算法设计，得出数量、均匀性和尺寸等参数.

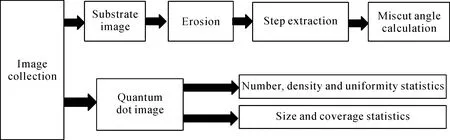
图1 基于机器视觉的衬底和量子点STM形貌分析系统框图Fig. 1 STM morphological analyzing system diagram of substrate and quantum dot based on machine vision

3 算法设计

3.1 衬底斜切角计算

采用具有合适斜切角的衬底，可改善外延层的表面形貌和晶体质量[8]. 斜切角是指对衬底沿着某一方向进行斜切时的角度. 斜切角计算流程如图1所示，利用图像腐蚀、台阶提取和斜切角计算，得出斜切角大小.

a.图像腐蚀

衬底图像如图2(a)所示，更为微观的结构在大尺度的STM图像上以细微纹理噪声的形式呈现，会对斜切角的自动识别与计算产生干扰. 使用腐蚀可以消除噪声的干扰，腐蚀公式如式(1)所示：

A⊙B={x:B(x)∈A}

(1)

其中A为被腐蚀图像，B为腐蚀图像所用结构元素. 腐蚀结果如图2(b)所示，纹理噪声基本消除.

图2 腐蚀图像Fig. 2 Erosion image

b.台阶提取

为获得台阶形状，需对图2(b)进行台阶提取，其流程如图3所示：

图3 台阶提取流程图Fig. 3 Flow chart of step extraction

台阶提取过程的核心为边缘检测，本文使用的边缘检测算子为Prewitt算子，如图4所示：

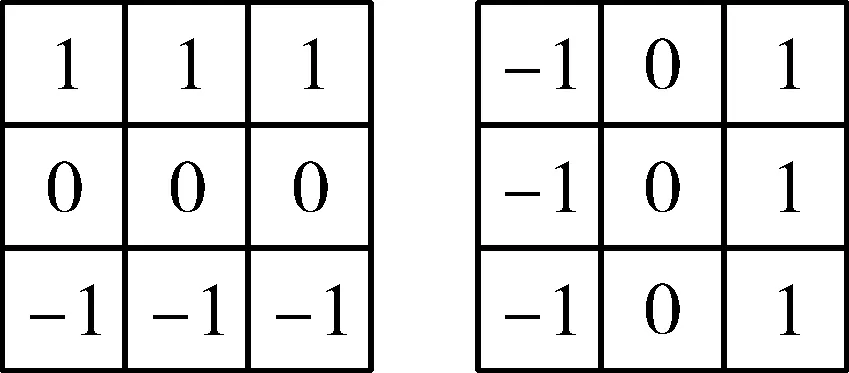
图4 Prewitt算子Fig. 4 Prewitt operator

对数字图像f(x,y)，Prewitt算子定义如下：

G(i)=|[f(i-1,j-1)+f(i-1,j)+

f(i-1,j+1)]-[f(i+1,j-1)+

f(i+1,j)+f(i+1,j+1)]|

(2)

G(j)=|[f(i-1,j+1)+f(i,j+1)+

f(i+1,j+1)]-[f(i-1,j-1)+

f(i,j-1)+f(i+1,j-1)]|

(3)

则

P(i,j)=max[G(i),G(j)]

(4)

或

P(i,j)=G(i)+G(j)

(5)

图5(a)是边缘检测的结果，为减少噪声干扰，根据像素面积大小滤除较小区域，得到台阶大致形状，如图5(b). 其中台阶2有细小断裂如图5(c). 为使台阶连接起来，使用闭运算，闭运算为对图像先膨胀，后腐蚀. 腐蚀公式如式(1)，膨胀公式如式(6)：

A⊕B={x:B(x)∩A≠φ|}

(6)

其中A为被膨胀图像，B为膨胀图像所用结构元素. 闭运算结果如图5(d). 为去除较小的断裂台阶，再次滤除较小区域，得到台阶形状如图5(e)所示. 对图5(e)进行细化处理，处理结果如图5(f).

图5 台阶提取Fig. 5 Step to extraction

c.斜切角计算

通过台阶提取，得到台阶形状. 为得到斜切角大小，需对台阶进行斜切角计算，计算方法：对图5(f)使用连通域提取，分别得到每层台阶. 以图6为例，依次计算相邻两层台阶距离，并根据图像实际尺寸按照比例转化成实际距离. 实际距离计算公式如式(7)：

图6 相邻台阶距离计算Fig. 6 Distance calculation for adjacent steps

(7)

其中(xi1,yi1)和(xi2,yi2)为与直线i相交的两台阶上的点，j和k为图像真实尺寸的长和宽，m和n为二值化图像矩阵的列和行. 由于每层台阶之间距离为0.28 nm，所以di的平均值与高度的比值即为正切值，通过反三角变化即可得出斜切角.

3.2 量子点数量和均匀性计算

量子点生长密度和均匀性对量子点器件的性能好坏有重要影响[6, 7]. 为使量子点的数量和均匀性计算更加高效，利用二值化和阈值下降对量子点进行计数，通过邻域密度计算分析均匀性.

a.量子点分割

二值化的量子点图像如图7所示，由于量子点所处的层不同，量子点图像呈现亮暗分布，采用单一亮度阈值，会存在粘连和亮度不均的问题.

图7 二值化的量子点图像Fig. 7 Binarizated quantum dot image

为解决这一问题导致的统计错误，提出一种基于阈值下降的二值化算法，算法流程如图8所示：

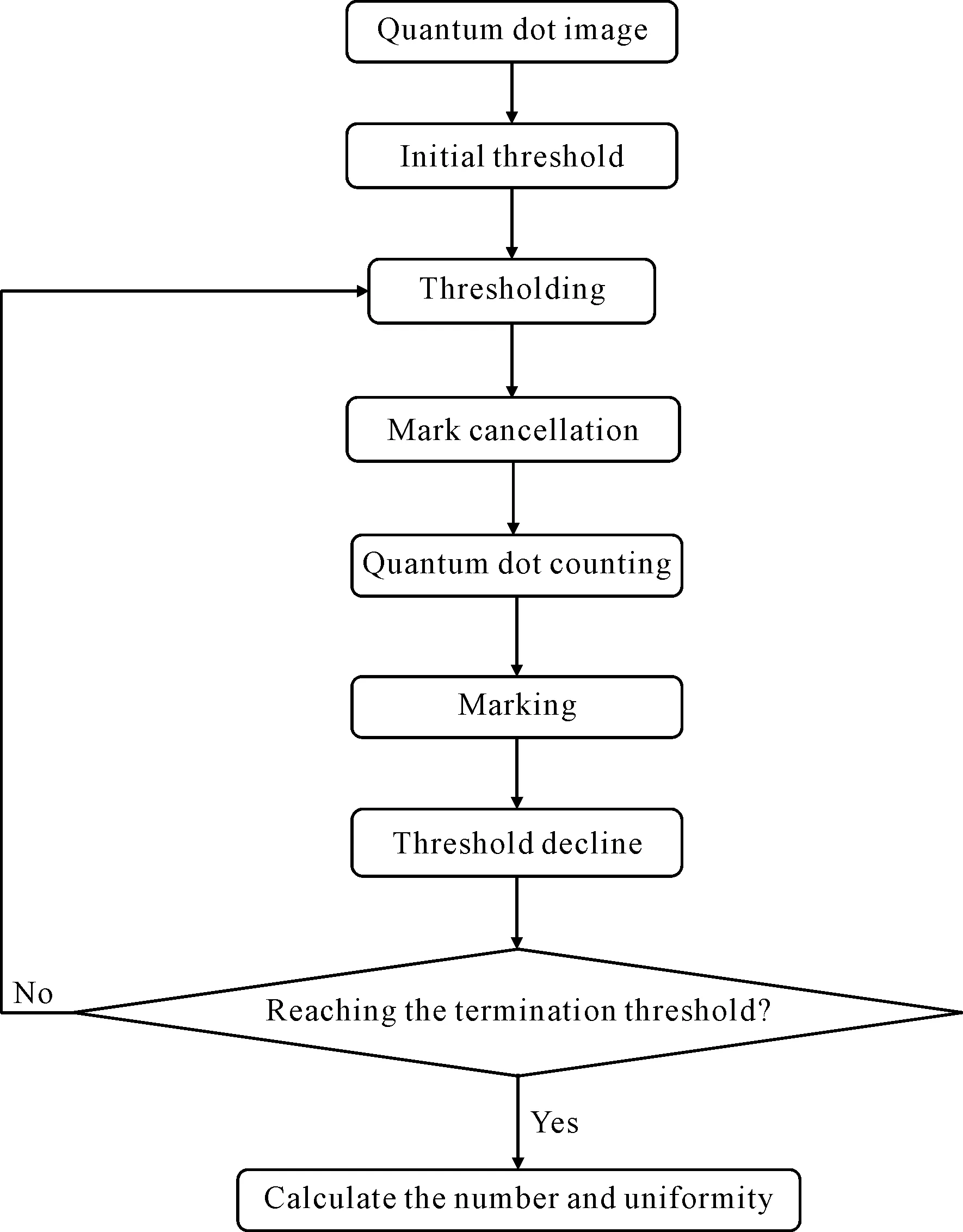
图8 数目和均匀性计算流程图Fig. 8 Calculation flow chart of number and uniformity

算法的主要目的是在阈值的逐渐下降的过程中，对每一次阈值下降得到的量子点进行统计. 由于背景部分不是量子点，不需要被显示，因此需要设定一个终止阈值. 图9所示为图7对应的对数直方图，由于背景部分灰度值占比较大，最大值之后的虚线即为就是终止阈值.

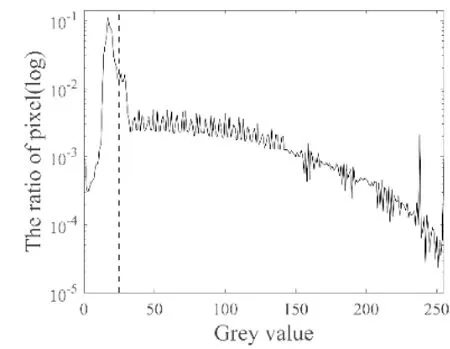
图9 灰度值对数直方图Fig. 9 Gray value logarithmic histogram

确定终止阈值和初始阈值后，从高阈值开始等步长扫描，逐步调低阈值. 随着阈值的降低，被统计的量子点会逐渐增加. 每一次扫描，对新发现的量子点进行标记并排除已标记的量子点. 其中标记方法为：将新发现量子点的重心坐标保存到矩阵G(x,y). 排除标记方法为：每个量子点和矩阵G(x,y)做逻辑与运算. 若相与后所有像素点的数值之和大于0，则该量子在之前操作中已被存入矩阵G(x,y)；若相与后所有像素点的数值之和等于0，则为新出现量子点，进一步进行连通域计数，并提取重心存入矩阵G(x,y)中.

b.量子点均匀性计算

量子点的邻域密度计算方式如式(8)所示，其中U(x,y,d)表示以(x,y)为中心，d为边长的正方形区域的量子点数目，d2表示区域面积. 区域中心(x,y)每次滑动一定的距离，计算密度并保存到矩阵M(x,y)中.

(8)

最大相对偏差公式如式(9)所示，选取这个评估参数对M(x,y)的密度均匀性进行分析.

(9)

3.3 量子点尺寸和覆盖率计算

量子点尺寸对量子点器件的性能有重要影响[6, 7]. 为使量子点的尺寸和覆盖率计算更加高效，通过阈值下降寻找未发生粘连的最大尺寸，并进行计算.

量子点图像如图10(a)所示，存在图像边缘量子点显示并不完整和粘连的问题. 为解决这一问题，在量子点分割的基础上，检测量子点是否完整，并计算量子点未发生粘连的最大尺寸. 计算方法为：1)对标记的量子点的图像进行反转，如图10(b)所示. 2)对反转后的图像求连通域(白色区域)个数，若连通域个数大于2，则量子点发生粘连. 检测到粘连后，阈值增加，返回量子点未发生粘连的最大阈值，如图10(c)所示. 3)检测二值化的量子点在图像边界上是否有像素，若有像素，说明量子点显示不完整，不对其进行尺寸计算. 尺寸计算的方法是将量子点看作是矩形，并计算长和宽，如图10(d) 所示. 当阈值下降到终止阈值时，计算未发生粘连的量子点尺寸.

计算所有量子点的像素点之和，并除以图像的总像素即可得到覆盖率.

4 结果与分析

4.1 斜切角的计算

本文对30张衬底图像进行了计算并与人工进行对比，表1中给出其中五张有代表性的衬底图像.

图10 量子点尺寸计算Fig. 10 Quantum dot size calculation

统计结果表明30张衬底图像的算法与人工计算的最大误差为8.48%，平均误差5.02%. 可见，利用机器视觉技术对斜切角的自动化计算有较好的协助作用.

4.2 量子点数量和均匀性计算

图11为对图7的量子点数目和密度归一化后的均匀性统计：

表1 机器视觉与人工计算的斜切角对比

Table 1 Comparison of miscut angles between machine vision and manual calculation

Image number12345ImageMachine vision/nm0.05770.03340.05160.04800.0563Manual calculation/nm0.05520.03340.04940.05230.0519

量子点的高低在图像中表现为灰度值的高低，所以阈值的增加表示量子点高度的增加. 图11(a)表示在0-255阈值区间的量子点数目统计，即一定高度区间的量子点数目统计. 图7的尺寸为1000 nm×1000 nm，计算得到量子点数目为396个，其整体密度为3.96×10-4个/nm2. 由图11(b)可知，量子点分布并不均匀，计算得出最大相对偏差为68.42%.

图12为误差统计散点图，可以看出误差均在0以上，说明量子点统计结果偏大. 其中200 nm×200 nm、500 nm×500 nm和1000 nm×1000 nm的量子点图像平均计数时间分别为2.009 s、2.923 s和7.658 s，平均误差分别为0.212 %、1.3496 %和0.7747 %，其整体平均误差为0.7788 %.

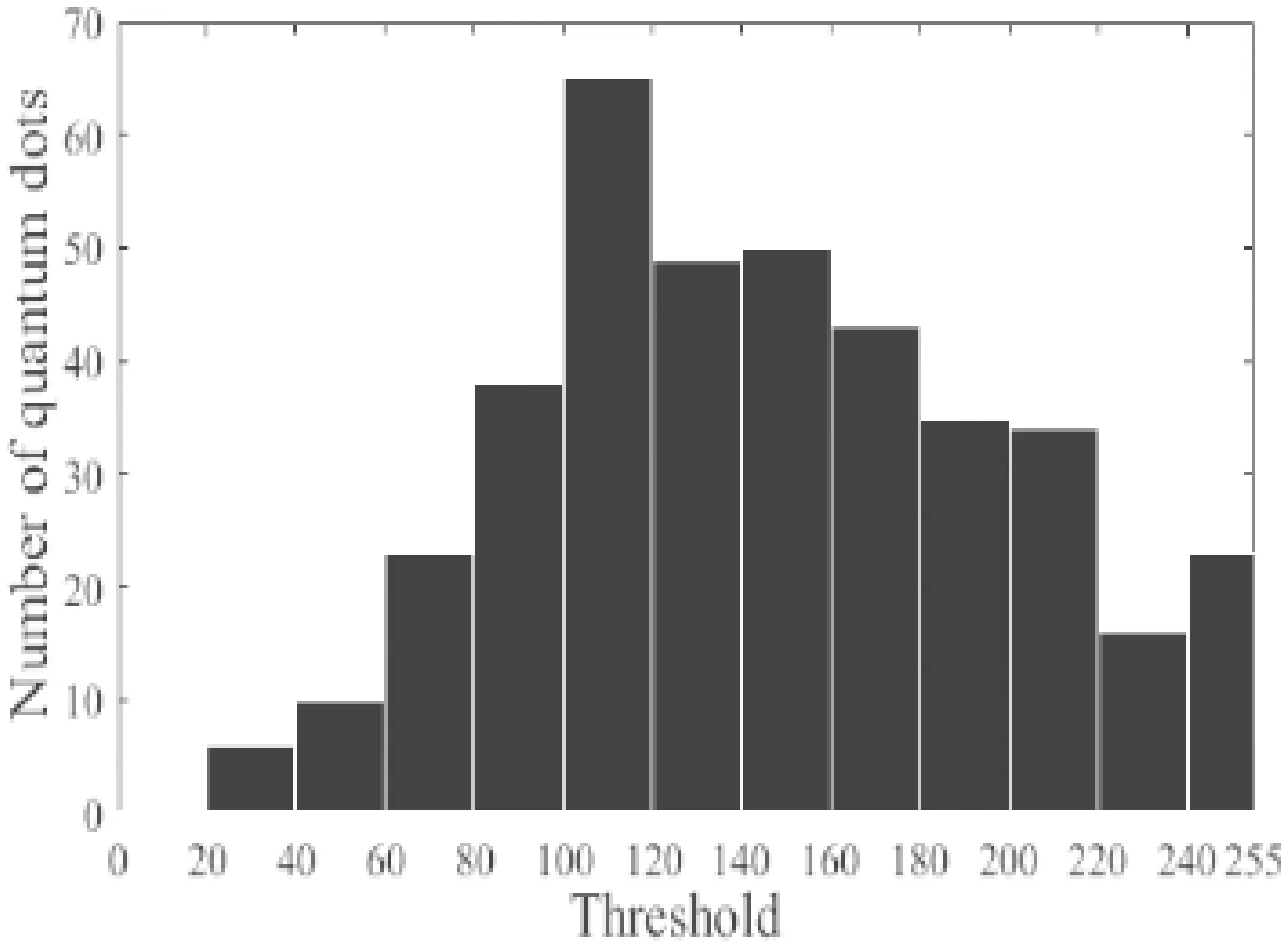
(a) Number statistics

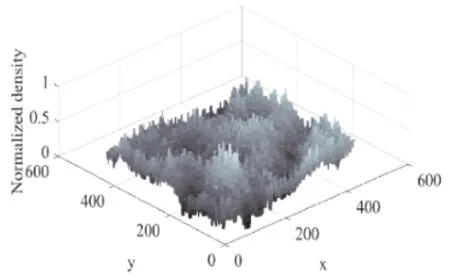
(b) Statistics of uniformity图11 量子点数目和均匀性统计Fig. 11 Quantum dot number and uniformity statistics

导致误差的主要原因：由于量子点计数的算法是根据亮度下降来计数的，当一个量子点较大、量子点上距离较远位置的亮度接近时，一个量子点会被计算为多个量子点，导致计数错误.

4.3 计算量子点尺寸

对图10(a)计算量子点尺寸和长宽比统计如图13所示：

图12 误差统计散点图Fig.12 Scatter plot of error statistics

图13(a)和13(b)为量子点尺寸统计，量子点尺寸在23 nm-29 nm和13 nm-19 nm占有较大的比重，计算得到其覆盖率为27.57 %. 由图13(c)可知，量子点长宽比大多分布在1.6-1.7之间.

图14为10(a)量子点尺寸计算误差图，由图14可知，量子点长和宽的计算误差均在±5%以内，即量子点长和宽的误差分别在±1.3 nm和±0.7993 nm以内. 且平均计算误差为1.12%. 可见，利用机器视觉技术对量子点尺寸的自动化计算有较好的协助作用.

图13 量子点尺寸统计Fig. 13 Quantum dot size statistics

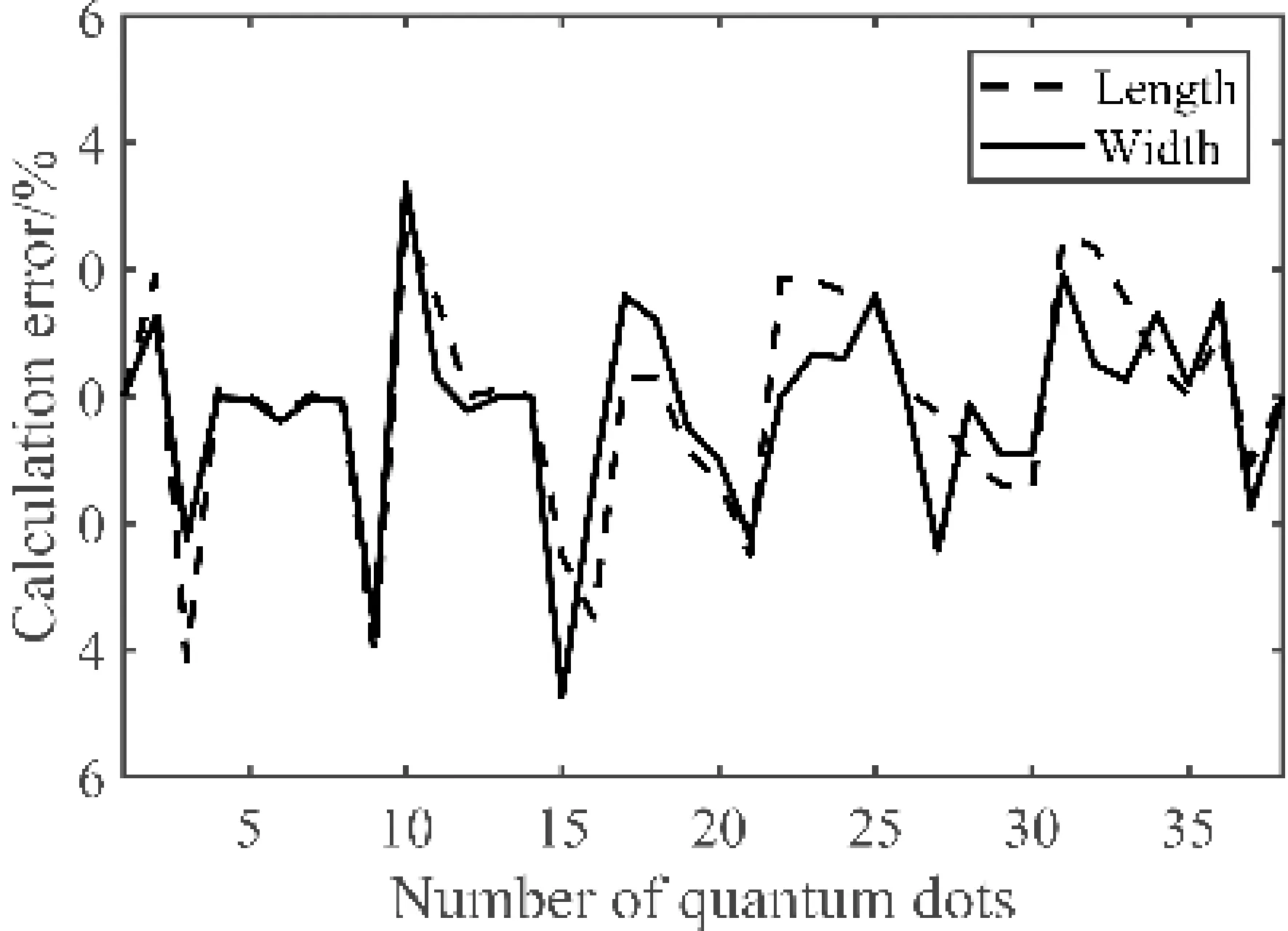
图14 量子点尺寸计算误差图Fig. 14 Calculation error diagram of quantum dot size

5 结 论

基于机器视觉对衬底和量子点的STM图像进行分析，计算斜切角、量子点数量、密度、均匀性、尺寸和覆盖率等表面形貌特征. 利用预处理和边缘检测提取台阶形状，并通过反三角变换实现斜切角计算；利用二值化和阈值下降实现量子点计数，通过邻域密度计算实现均匀性分析；在量子点计数算法的基础上寻找量子点未发生粘连的最大尺寸，实现量子点尺寸的计算. 实验结果显示，斜切角、量子点计数及尺寸的平均误差分别为5.02 %，0.7788 %及 1.12 %. 基于机器视觉的算法具有较高的精度和速度，可以实现衬底和量子点形貌特征图像的自动识别，对协助研究者分析量子点表面形貌有实际意义.