CrI3高压相变及其光学性质理论研究

张丽琴, 袁五届, 张金峰, 徐士涛

(淮北师范大学信息学院， 淮北 235000)

1 引 言

伴随着碳六元环组成的石墨烯被Geim小组[1]成功分离，二维材料在电学[2]、磁学[4,5]、光学[6,7]、热学[8]等方面所展示出来的独特魅力，引起科学家的关注. 随着科学家在理论研究和应用领域的不断探索及深入研究，越来越多的二维材料被相继找到. 如过渡金属硫族化物(TMDS)[9-11]，其体材料具有间接能隙，单层变成直接能隙半导体且价带劈裂成两个自旋极化的能带；同时通过施加极化强光，发现单层具有剧烈的光吸收现象. 他们独特的电子结构和光学性质使其在光电子器件上具有非常广泛的应用前景[12-28]. 进一步的研究发现，单层黑鳞具有各项异性的能带结构[14, 15]. 更加奇异的是，随着层数的增加，带隙变的连续可调[18, 19]，这个使其在低维压电材料中的应用成为可能. 随着维度的减小[17,24]，单层二硫化钼(MoS2)在层间耦合效应消失的同时[25,27]，其体相也由间接带隙半导体变成单层的直接带隙半导体且谷自旋效应得以实现[21,29].

然而，大多数二维材料，包括石墨烯等，都不具有本征铁磁性. 尽管可以通过磁原子掺杂和磁近邻效应等方法引入铁磁性，但在二维半导体中实现长程有序的自旋排列面临巨大挑战. 两维的CrI3是非常罕见的本征铁磁半导体[29,30]. 徐晓栋教授和他的合作团队从实验上论证了CrI3随着层数的不同，展现出跟体相完全迥异的物理性质. 实验证实，单层的CrI3成为具有面外自旋取向的Ising铁磁体. 双层CrI3所展现出的磁性受到了抑制，而三层CrI3则显示，其被抑制的铁磁性得到了修复. 这使得两维CrI3在磁传感器以及信息存贮方面有着极大的应用前景. 理论上，zhang等人[27]详细研究了体相下CrI3的磁性及其光学性质. 并进一步验证单层CrI3的电子、光学和磁性性质. 然而，到目前为止，理论上鲜少涉及体相材料CrI3结构及其光学性质. 本文基于第一性原理的理论计算，对体相材料CrI3的上述性质进行了详细的分析.

2 基本理论和方法

在本文中，利用基于密度泛函理论的第一性原理平面波软件包CASTEP计算体相CrI3极性条件下及电子性质和光学性质[31,32]. 采用Perdew-Burke-Emzerhof(PBE)作为交换关联泛函，用缀加投影赝势波描述离子实和价电子间的相互作用[33]. 采用广义梯度近似(GGA)的PBE泛函处理电子之间的相互交换关联作用.

首先，计算不同压强下体相CrI3的电子性质和光学性质. 在计算过程中选取截断能为750 eV，布里渊区K点网格为9×8×8. 其次，计算的平面波基组采用700 eV截断能，布里渊区K点的积分网络由Monkhorst-Pack形式产生,总能量的收敛精度为10-5eV. 结构优化和计算的网络分别为3×3×1和9×9×1.

3 结果与讨论

3.1 体相CrI3的几何结构和稳定性

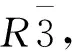
3.2 体相CrI3的能带密度结构

在不考虑电子自旋的情况下，通过广义梯度近似计算(GGA)得到体相CrI3的能带结构，如图1所示，从图中可以清晰的看出，在零压常温下得到的禁带宽度为3.204 eV,远远高于Dillon团队[35]于1964年所测量的实验值1.2 eV. 实验值跟理论值出现了接近三倍的偏差，究其原因，一是CrI3是一种磁性材料半导体，没有考虑其自旋. 二是因为Cr原子含有d轨道，存在较强的旋轨耦合和强关联，没有加入U. 考虑到电子的自旋及其存在的d轨道而导致的强关联耦合，得到如图2所示. 从图中可以看出，CrI3的禁带宽度是1.09 eV的半导体，与已经存在的实验值非常接近. 结合图3的能态密度图，可以看出，在Fermi能级附近，参与轨道成键的主要来自于I的p轨道和Cr的4d轨道. Cr的4d轨道能带宽度比较大，说明Cr 4d轨道参与了成键. 同理，I的5p轨道在Fermi能级附近参与了成键. 在Fermi能级附近，I的5p轨道和Cr 4d轨道能带较宽且态密度的峰值比较尖锐，说明在这些位置，离域性强且存在较强的轨道自旋耦合. 因为带越宽，成键越强，态密度峰跨度越大，离域性越强，成键越强，轨道自旋耦合越强. 考虑到包利不相容原理，I的5p轨道由于存在较大的电负性而Cr 4d轨道金属部分容易失去电子而对原子轨道的贡献较少. 考虑到电子的自旋以及轨道耦合，可知随着成键作用的加强，成键分子轨道下移而反键分子轨道上移. 自旋向上的原子的成键轨道下移而自旋向下的反键原子轨道上移，导致能带变窄.

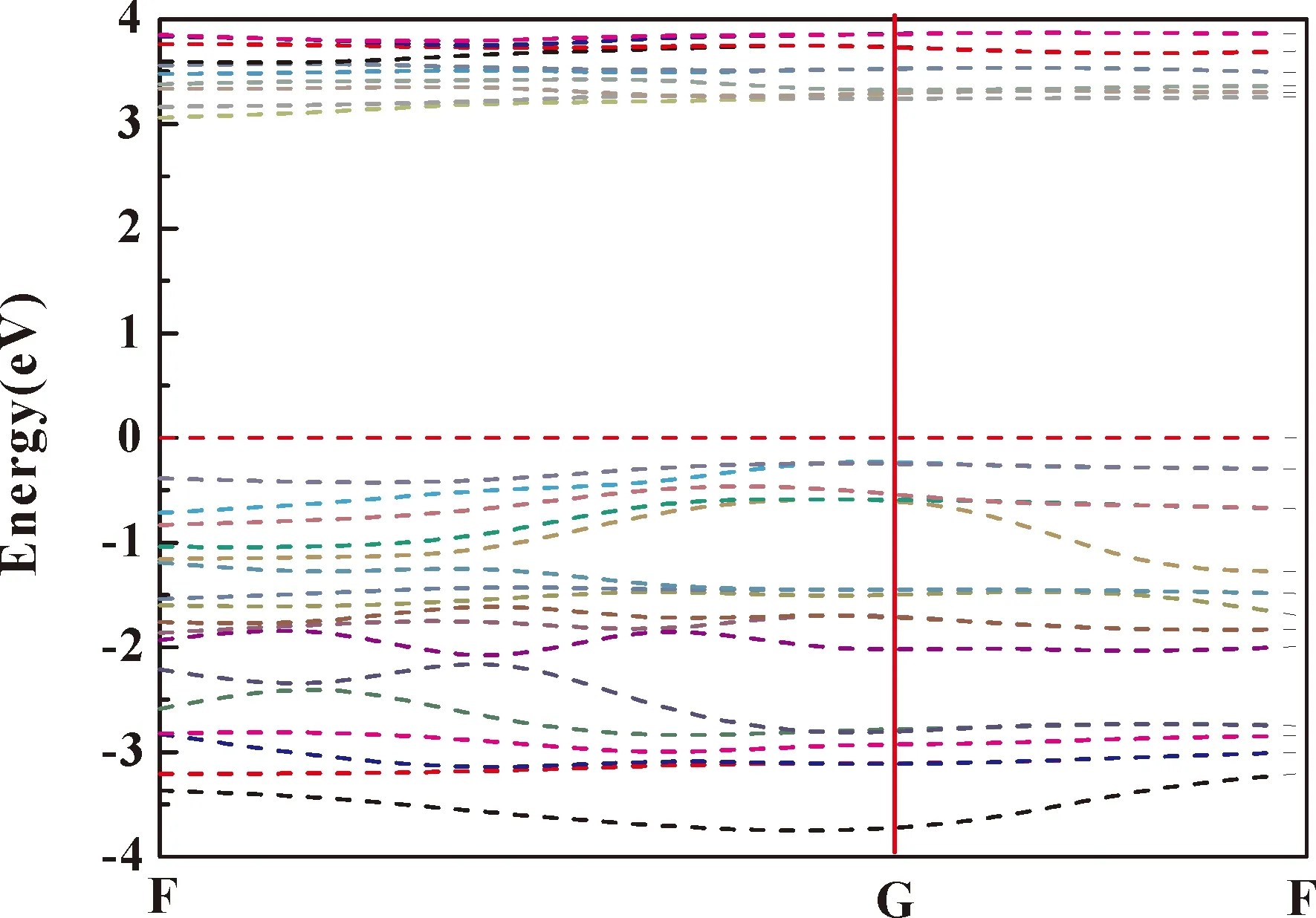
图1 零压下不考虑电子自旋及其关联耦合时的能带图Fig. 1 Energy band diagrams at zero pressure without considering electron spin and associated coupling

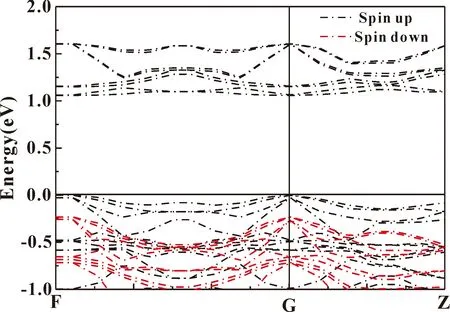
图2 零压下考虑电子自旋及其关联耦合的能带图Fig. 2 Energy band diagrams at zero pressure considering electron spin and associated coupling

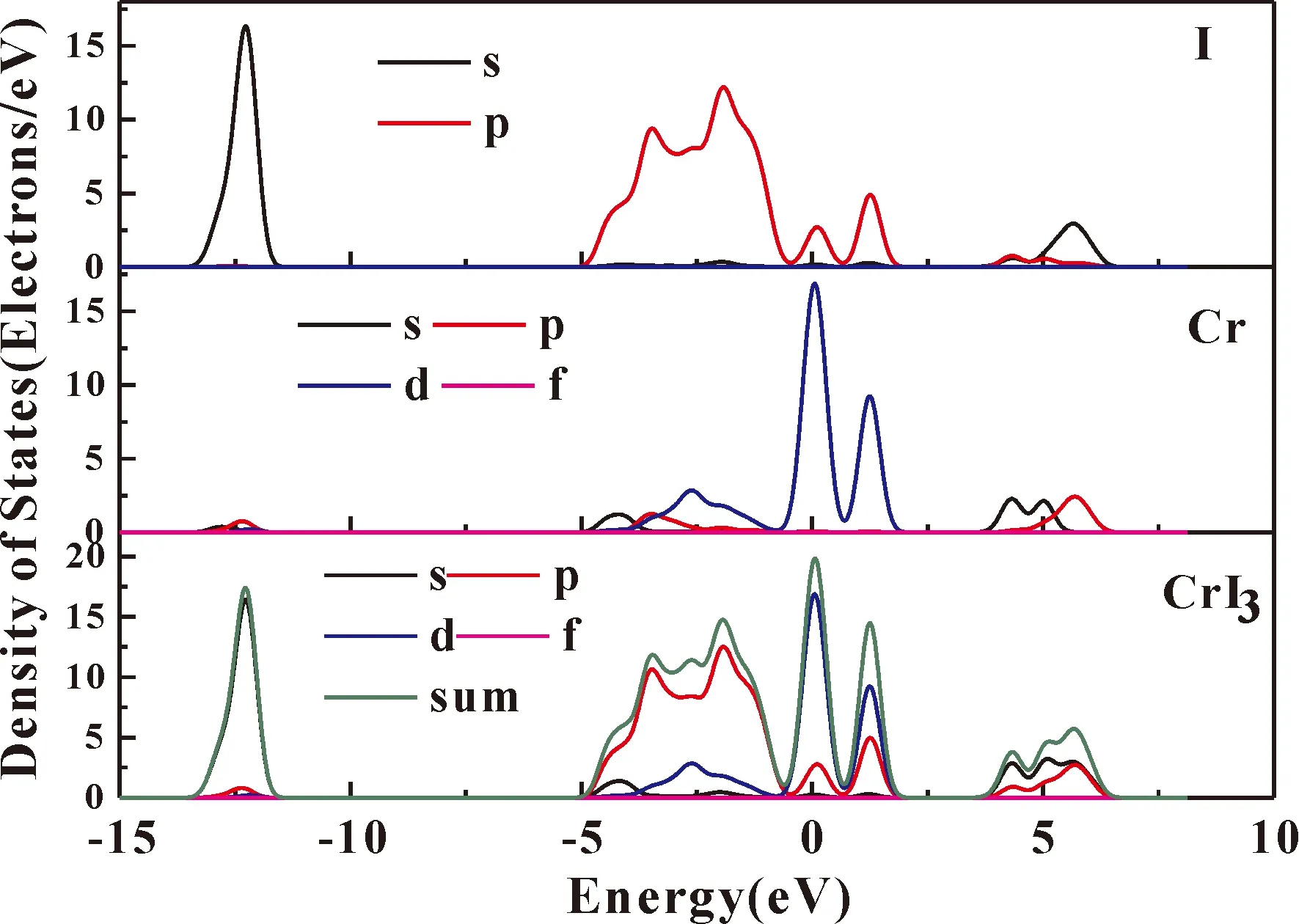
图3 零压下CrI3态密度图Fig. 3 Density of states of CrI3 at zero pressure

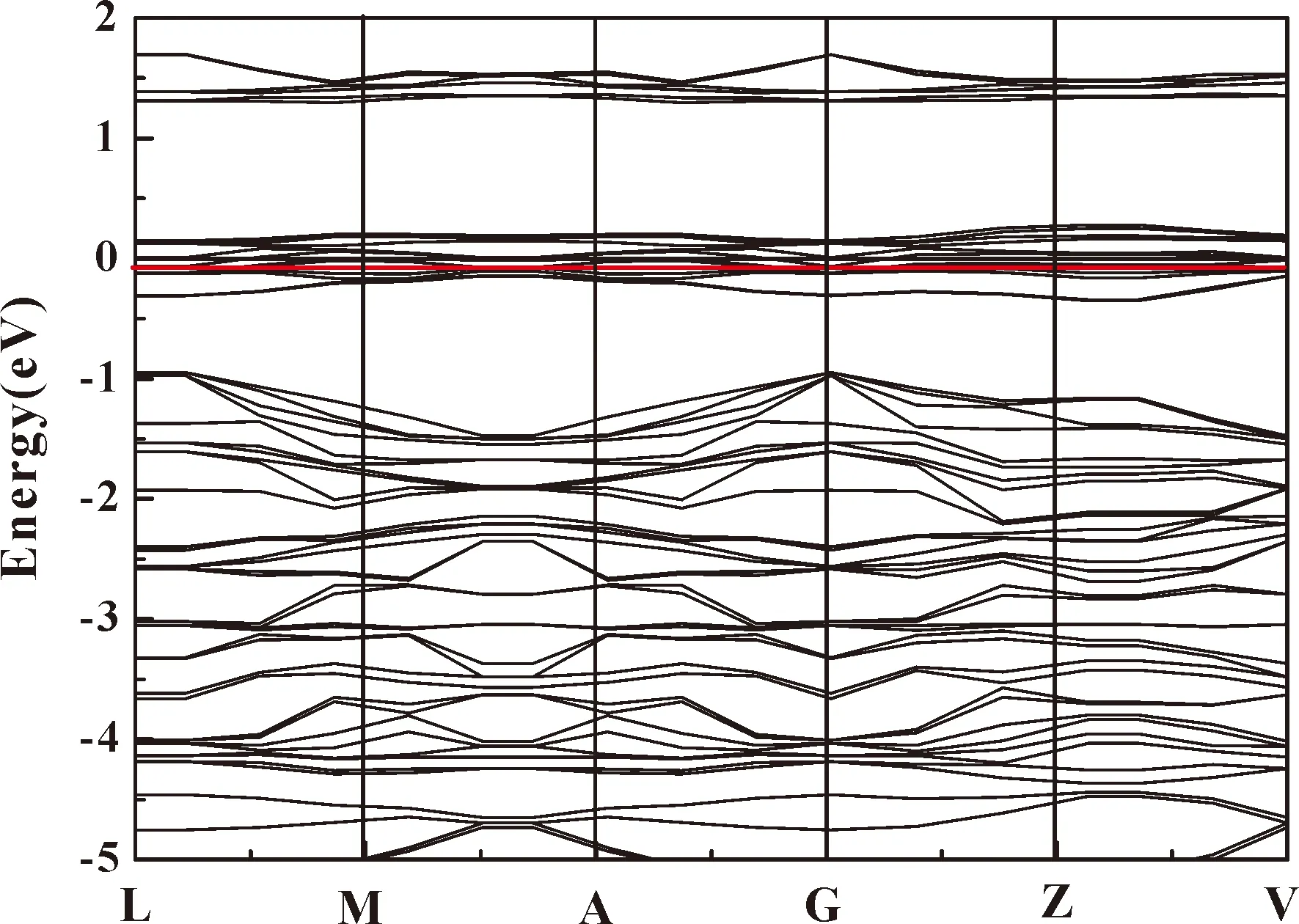
图4 P=26.1 GPa CrI3的能带图Fig. 4 Energy band diagrams at pressure 26.1 GPa of CrI3 considering electron spin and associated coupling

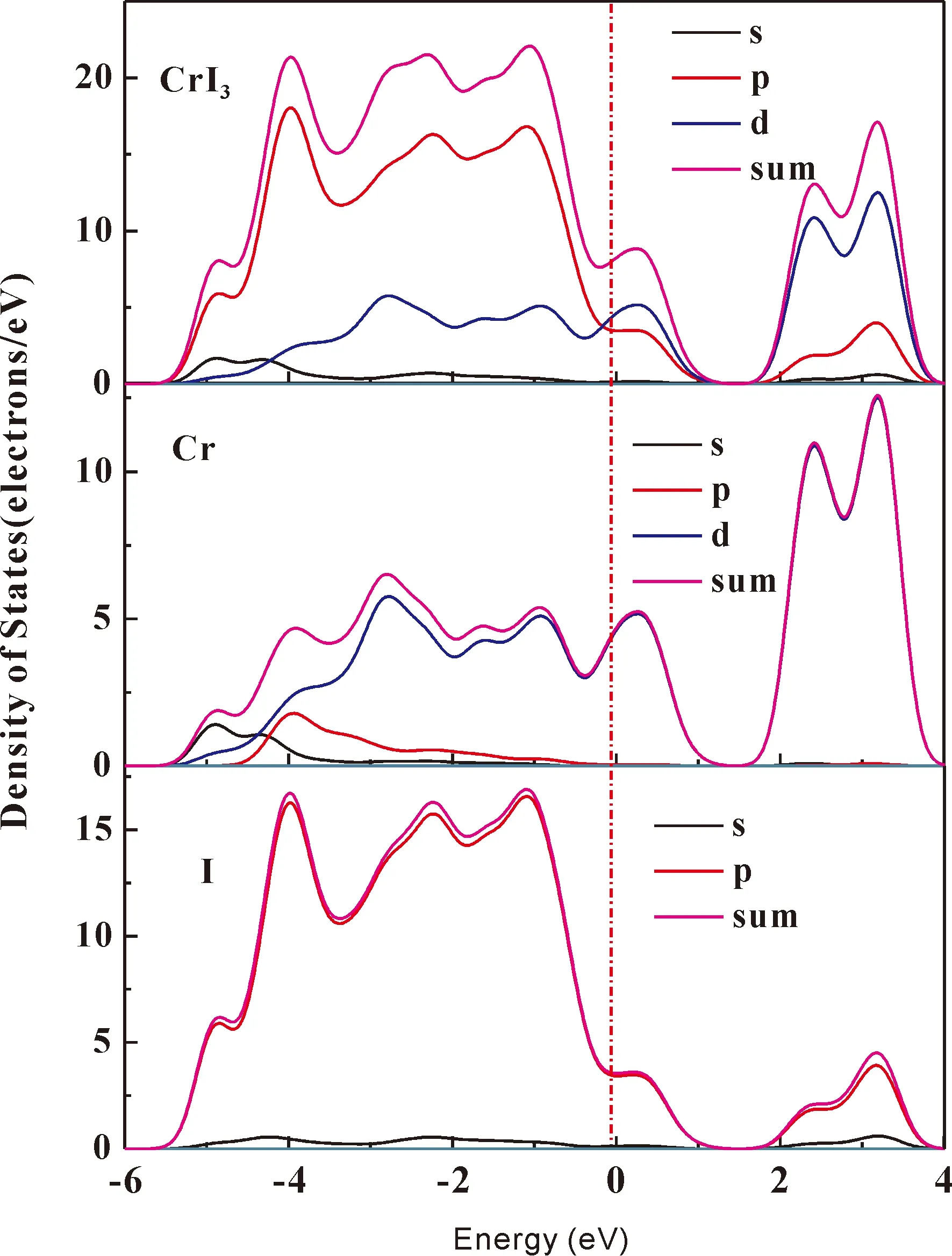
图5 P=26.1 GPa CrI3的态密度图Fig. 5 Density of state diagrams of CrI3 at pressure 26.1 GPa considering electron spin and associated coupling

3.3 体相CrI3的差分电荷密度

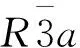
图 6 体相CrI3分别在到C2/m相是的差分电荷密度图Fig. 6 Differential charge density diagram of CrI3 at phase and phase C2/m

3.4 体相CrI3的光学性质

物质的光学性质对研究其在光学成像，光学器件的制备，传感技术，机械工程技术方面有举足轻重的作用. 在光电子物理、凝聚态光谱、半导体光电子物理已经得到广泛的应用. 本文通过计算体相CrI3的吸收谱、介电函数、反射谱、损失函数等光学性质来进一步了解其物理性质. 利用能带结构，跃迁矩阵和电子态密度，可以推导得到介电函数的实部、虚部、折射率、吸收系数、消光系数等. 利用Kramas-Kronig关系，得到关于介电函数的实部和虚部之间的关系.

f(kn)×(1-f(kn′)δ(Ekn-Ekn′-ħω)

(1)

(2)

其中，n和n′分别表示导带和价带,f(kn)为第一布里渊区的动量矩阵元，根据公式[1]和[2]我们可以得到吸收系数、折射率和消光系数.

吸收系数

(3)

折射率

(4)

消光系数

(5)

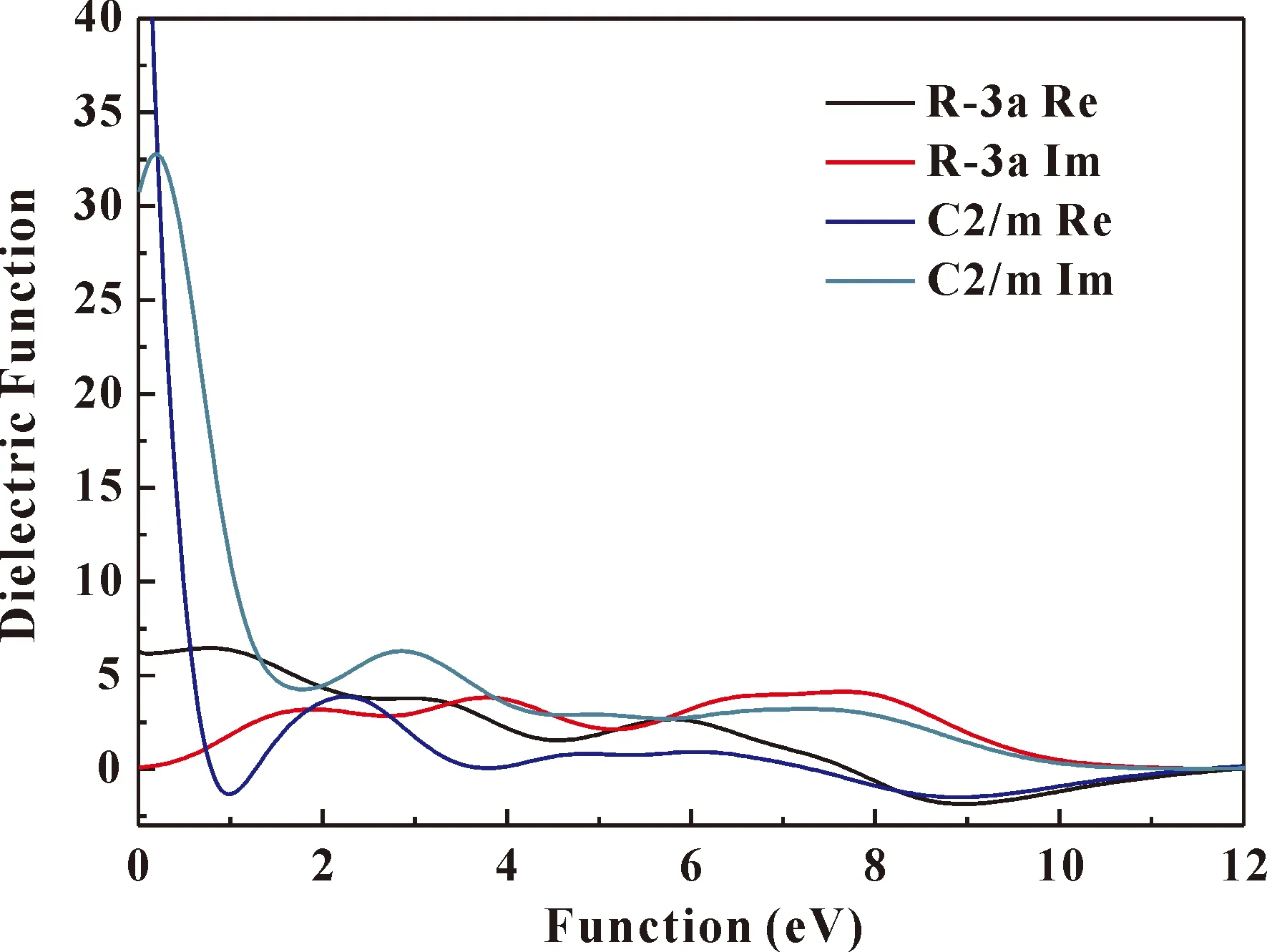
图 7 体相CrI3分别在到C2/m相时的介电函数Fig. 7 Dielectric functions of CrI3 at structural and C2/m respectively

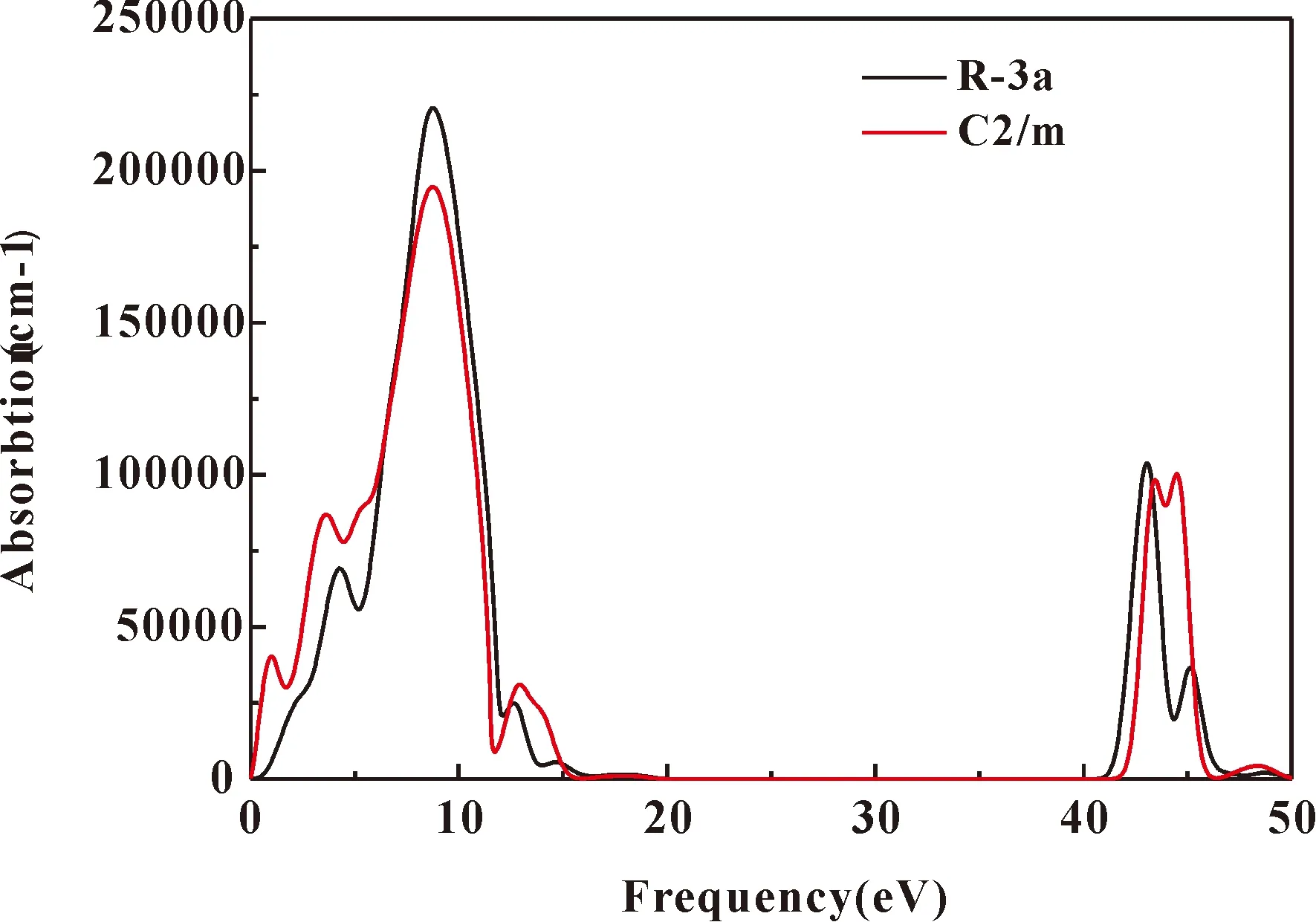
图 8 体相CrI3分别在到C2/m相时的吸收谱Fig. 8 Absorption spectra of CrI3 at structural a and C2/m respectively

折射率和消光系数分别来源于复折射率的实部(n)和虚部(k)，折射光谱、消光光谱在近红外区域电子跃迁非常活跃. 可见区域2.0 eV-5.0 eV附近，电子的折射光谱与消光光谱都对应一个相当宽的频率区间. 复折射率的实部(n)在虚部(k)上升和下降的斜率处分别出现了极值，这与其谱线的峰值较多是相对应的，均由于体相CrI3能带结构弥散性相比较强引起的变化.

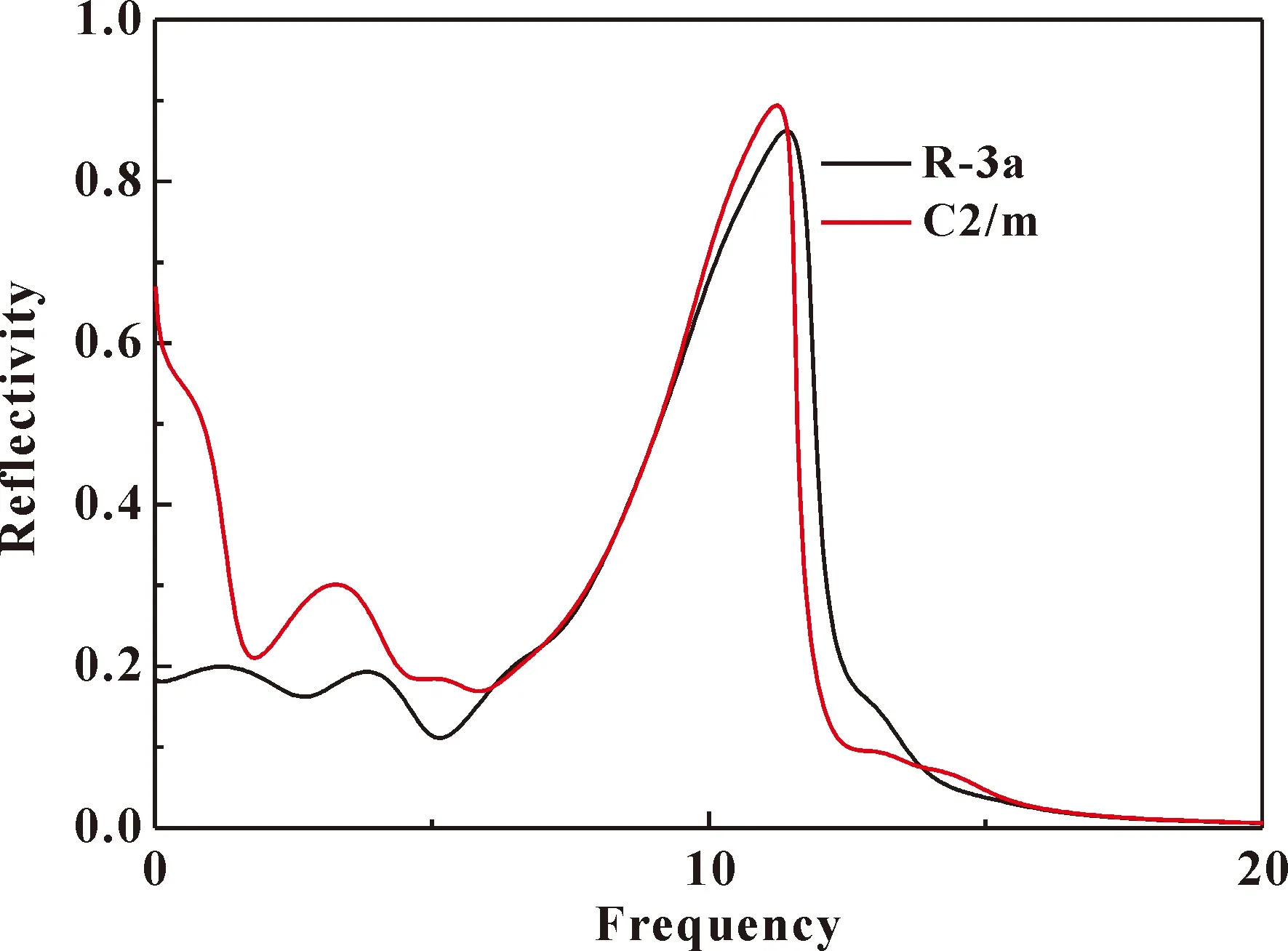
图9 体相CrI3分别在到C2/m相时的反射谱Fig. 9 Reflectivity spectra of CrI3 at structural and C2/m respectively

图10 体相CrI3分别在到C2/m相时的折射谱Fig. 10 Reflective index of CrI3 at structural and C2/m respectively

4 结 论