基于排队论的公共自行车系统自平衡问题研究

万圆圆

（上海交通大学 安泰经济与管理学院，上海 200030）

随着人们生活质量和购买力水平的提高，城市家用轿车的持有量呈现放量式增长的态势，导致城市公共空间变得拥挤，交通拥堵问题日益严峻。此外，人们对绿色环保、节能减排等问题日渐重视，绿色出行的概念也越来越受到人们的关注。公共自行车系统的出现，一方面能够缓解城市交通的压力，同时解决公共交通“最后一公里”的问题，另一方面能满足人们对于低碳、环保、健康的交通方式的需求。因此，公共自行车系统的建设得到了世界各国和各地区政府的重视，成为公共交通的重要发展方向。

我国公共自行车系统起源于2008年5月开始运营的杭州公共自行车系统，此后公共自行车系统在全国各地迅速发展。据中国交通与发展政策研究所统计，截至2017年底，我国共有170多个城市和地区的政府发起建设了公共自行车系统，运营自行车数量近100万辆。随着共享经济理念的兴起，以互联网作为媒介，借助智能手机支付技术的大发展，诞生于校园的共享单车也快速进入中国各大城市。据统计，截至2017年4月，中国的共享单车运营企业数量已达45家，共投放自行车约720万辆。

可见，目前国内的公共自行车系统主要有两种模式，其一为政府主导的有桩公共自行车系统，其二为社会资本支持的无桩共享单车模式。两种模式在运营过程中各自存在着一些问题，也有一些共同的问题。比如，公共自行车系统存在操作复杂、借还车困难等问题，而共享单车则存在无序停放、对用户行为监管困难等问题。然而不管是哪种运营模式，由于用户借还车行为的不规律性和不确定性，都存在车辆分布不均的问题，需要花费大量的人力和成本去调度不同区域的自行车数量。本文所研究的问题就是通过激励用户从车辆较多的区域借车或到车辆较少的区域还车，从而影响用户行为，改变部分用户借车或还车的租赁点，从而实现公共自行车系统的自我平衡，减少需要调度的自行车数量，提高运营效率，降低管理成本。

目前，国内外学者对于公共自行车系统的研究主要分以下几个方向：一是对于借还车需求预测的研究，二是对于公共自行车系统车辆调度问题的研究，三是公共自行车租赁点选址的研究。在公共自行车的车辆调度问题上，国内外学者主要做过以下研究：一是基于需求预测的调度问题研究；二是调度车辆路径规划问题研究；三是多阶段、动态公共自行车系统调度问题的研究等。本文所研究的公共自行车系统自平衡问题目前较少有学者研究，仅有的少量研究也是基于同质化的站点，而本文则考虑了不同站点的用户借还车到达率不同，通过建模和仿真给出了系统自平衡方案。

1 建立模型

1．1 基础模型

本文研究的是一个拥有n个自行车租赁点的有桩公共自行车系统，该系统共运营m辆自行车。对于单辆自行车而言，可能存在两种状态：被锁在某个租赁点或正在被用户使用。每一个租赁点拥有有限个车桩可供用户借车或还车，因此对于单个租赁点而言可能存在三种状态：无可用自行车、无空闲车桩、既有可用自行车又有空闲车桩。若一个自行车租赁点无可用自行车，则用户无法在该租赁点借车并离开系统；若一个自行车租赁点无空闲车桩，则用户无法在该租赁点还车并离开该租赁点继续骑行。

假设各租赁点的借车用户和还车用户分别服从泊松分布，不同租赁点之间相互独立。相关的参数设置如下：

n—自行车租赁点个数；

m—所有自行车数量；

λi—第i个租赁点还车用户的到达率；

μi—第i个租赁点借车用户的到达率；

ci—第i个租赁点拥有的车桩数量；

xi（t）—第i个租赁点在t时刻拥有的自行车数量。

不妨将所有正在被用户使用的自行车看作一个租赁点，并记为租赁点0。记租赁点0的还车用户到达率为λ0，借车用户到达率为μ0，拥有车桩数量为c0，在时刻t拥有自行车数量为x0（t）。当有用户从其他租赁点借车时，租赁点0的自行车数量增加1辆；当有用户从其他租赁点还车时，租赁点0的自行车数量减少1辆。可得记某时刻该公共自行车系统的状态为S＝｛x0，x1，x2，…，xn｝，其中本文将该公共自行车系统作为一个排队论过程进行研究，在自然状态下S的生灭过程如下图所示。

不妨设状态S的稳态概率为Px0，x1，x2，…，xn，则由上图易得S的状态转移方程如下：

1．2 推荐模型

基于以上设定，本文通过推荐用户更改还车租赁点的方式，来影响用户的还车到达率，从而减少需要调度的自行车的数量。当一个自行车租赁点无可用自行车时，我们需要从其他租赁点调入自行车；当一个租赁点无空闲车桩时，则需要将部分车辆调配到其他租赁点。因此，若要减少需要调度的自行车数量，一个有效的方法是降低各租赁点无可用自行车及无空闲车桩的概率。令ex0，x1，x2，…，xn表示状态S下无可用自行车的租赁点的数量，fx0，x1，x2，…，xn表示无空闲车桩的租赁点的数量，则在状态S下需要调度的租赁点的比例为（ex0，x1，x2，…，xn＋fx0，x1，x2，…，xn）／n，可得 该 公共自行车系统需要进行调度的概率Q为

为了改变用户的还车行为，我们以概率h′ij推荐到达租赁点i还车的用户将自行车还到租赁点j。假设用户以概率αij接受我们给出的推荐方案，则可得到达租赁点i还车的用户实际上以hij＝h′ij*αij的概率将自行车还到租赁点j。因此，我们不妨设以概率推荐到达租赁点i还车的用户将自行车还到租赁点j，用户以概率1接受我们给出的推荐方案，则租赁点i的实际还车到达率λ′i为

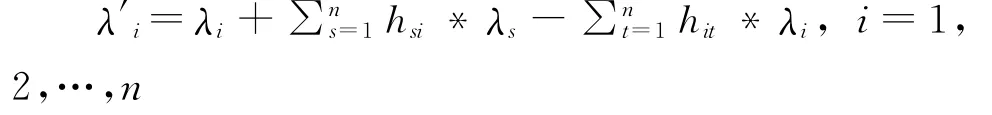
其中，hii表示不对到达租赁点i还车的用户推荐的概率，∑nj＝1hij＝1。

综上，为了降低需要进行调度的概率，可得如下规划问题：

易知，上述规划问题的复杂性会随着n的增大而增加，当n较大时，上述问题难以直接求解。因此，本文考虑各租赁点之间的独立性对上述问题进行化简。当用户到达租赁点借车时，若租赁点自行车数量不为0，则用户借车后离开该租赁点；若租赁点无可用自行车，则假设用户直接离开该系统，所以用户的借车行为不会对其他租赁点产生影响。同理，当用户到达租赁点还车时，若租赁点有空闲的车桩，则用户还车后离开该租赁点；若租赁点无空闲的车桩，则假设用户离开该租赁点继续骑行，所以用户的还车行为也不会对其他租赁点产生影响。因此，我们不妨假设所有租赁点之间相互独立。设租赁点i的稳态概率为Pxi，0≤xi≤ci，则

考虑单个租赁点i，其生灭过程如下：

其状态转移方程为

2 仿真实验

2．1 实验设定

本文仿真实验部分的数据来自美国华盛顿哥伦比亚特区（Washington D．C．，以下简称华盛顿）的公共自行车租赁系统——Capital Bikeshare。它是美国最大的公共自行车租赁系统，覆盖了哥伦比亚特区，以及周边的阿林顿、费尔法克斯等若干城市，24小时为居民提供自行车租赁服务。自2008年成立以来，该公共自行车系统已经运营了9年多的时间，租赁点的设置已经十分完善，用户来源也较为稳定。

该公共自行车系统目前拥有440个租赁点、3700多辆自行车以及7555个车桩。本文所采用的是2016年9月1日—2016年9月30日的344246条借还车数据，数据记录了借车时间、还车时间、借还车间隔时间、借车站点、还车站点、自行车编号以及是否注册会员等信息。本文以Capital Bikeshare的用户借还车数据作为初始借还车需求，并以此为基础计算不同策略下的调度数量，研究用户借还车行为改变后运营效率的变化。考虑到实际问题中用户借车的地点较难改变，因此本文仅考虑通过推荐新的还车点改变用户的还车行为。

由上文可知，为了使得需要进行调度的概率尽可能小，我们需要以概率hij推荐到达租赁点i还车的用户将自行车还到租赁点j，从而使得租赁点i的实际还车到达率λ′i＝μi，即使得单个租赁点在足够长的时间内，借车的用户数与还车的用户数相等。假设在足够长的观察期内，有Oi个用户到达租赁点i借车，Ii个用户到达还车，则我们可以通过求解…，n来计算推荐概率hij。

然而在实际问题中，由于距离等因素的限制，通常无法实现这一理想状态。公共自行车属于短途交通工具，用户接受推荐的概率会随着租赁点i、j之间距离的增加而降低，且当距离超过一定范围后，用户几乎不会接受推荐方案。因此，我们只能在一定的距离范围内进行推荐，使得I′i尽可能地接近Qi。结合实际情况，为及时满足用户需求，本文采取推荐与调度相结合的方案来平衡公共自行车系统。

在初始状态下，我们将全部3700辆自行车，根据车桩的数量按比例分配到各个租赁点，租赁点自行车数量记为S0＝｛s1，s2，…，sn｝，si表示租赁点i的初始自行车数量。记在时刻t时，租赁点i的自行车数量为xi（t），则在时刻t＋1时，若有Qi（t）个用户到达租赁点i借车，Ii（t）个用户到达还车，则xi（t＋1）＝xi（t）－Oi（t）＋Ii（t）。若xi（t＋1）＜0，则租赁点现有自行车无法满足用户的借车需求，需从其他租赁点调度－xi（t＋1）辆自行车到租赁点i；若xi（t＋1）＞ci，则租赁点现有空闲车桩无法满足用户的还车需求，需将xi（t＋1）－ci辆自行车调度至其他租赁点。在调度的过程中，由于调度成本的主要影响因素是租赁点间的距离，因此当某个租赁点无可用自行车时，需要在满足其他租赁点需求的前提下，从距离相对较近的若干个租赁点调度一定数量的自行车，以满足该站点用户的需求。同理，当某个租赁点无空闲车桩时，需要将部分车辆调配到距离相对较近的若干个租赁点。

在时刻t，若xi（t＋1）＜0，假设从租赁点j调度yj辆自行车到租赁点i，令dij表示租赁点i与租赁点j之间的距离，则求解如下线性规划问题可得各租赁点的调度量yj：

易看出当上述线性规划取最优解时，需在有多余车辆的租赁点中选择距离最近的租赁点调度，若仍不能满足租赁点i的需求，则继续从第二近的租赁点调度，如此重复直至调度量能够满足租赁点i的需求为止。因此，在本文的仿真实验中，当租赁点i无可用自行车时，采用的具体调度流程如下：

Step1：将其余租赁点按与租赁点i的距离从小到大进行排序，记为i1，i2，…，in－1，令k＝1，R＝Oi（t）－Ii（t）；

Step2：令H＝x ik（t）－Oik（t）＋Iik（t），若H≤0，跳到Step3；若0≤H＜R，则从租赁点ik向i调度H辆自行车，R＝R－H，跳到Step3；若H≥R，则从租赁点ik向i调度R辆自行车，并停止循环；

Step3：k＝k＋1，重复Step2。

同理，当租赁点i无空闲车桩时，用类似方案将自行车调度到附近租赁点，细节不再赘述。每次调度时，记录调度自行车的数量，并在最后进行求和即可得总的调度量。

2．2 实验方案

本文将Capital Bikeshare系统在2016年9月1日至2016年9月30日共30天的借还车数据作为初始需求输入，当用户到达租赁点借车而租赁点没有可用的自行车，或用户到达租赁点还车而租赁点没有空闲的车桩时，则按上文所述的方案进行调度。为便于计算，不考虑调度时间，即假设调度所需的时间为0。为衡量推荐策略对系统运营效率的提高，本文考虑无推荐的初始方案、无距离限制的理想推荐方案以及考虑距离因素的合理推荐方案三种情况，并记录三种情况下需要调度的自行车数量，以此研究推荐方案的可行性。三种方案的具体实验流程如下：

（1）初始方案：在初始方案中，我们考虑自然状态下不做任何推荐的情况。在仿真实验中，我们将时间划分为长度为15分钟的时间窗，并计算每个时间窗内各租赁点总的借车需求Oi（t）和总的还车需求Ii（t），则租赁点i的实际需求，即自行车数量的变化为Di（t）＝Ii（t）－Oi（t），Di（t）＞0则实际需求为还车需求，Di（t）＜0则实际需求为借车需求。记时间窗t结束时租赁点i的自行车数量为x i（t），则x i（t＋1）＝x i（t）－Oi（t）＋Ii（t）。若x i（t＋1）＜0，则需从其他租赁点调度－x i（t＋1）辆自行车到租赁点i；若x i（t＋1）＞ci，则需将x i（t＋1）－ci辆自行车调度至其他租赁点。计算总调度数量A。

（2）理想方案：在理想方案中，我们不考虑距离等因素的限制，可以将用户推荐至系统中任意租赁点还车，假设用户100%接受推荐方案。由上文可知，我们可以通过求解I′i＝Ii＋∑ns＝1hsi*Is－∑nt＝1hit*Ii＝Oi，其中i＝1，2，…，n来计算推荐概率h ij，但由于该方程组的等式数量远小于未知变量的数量，因此有无穷多解，我们将增加一些约束条件以获得最优解。令Qij＝Ii*hij表示从租赁点i推荐至租赁点j的用户数，则租赁点i的净流入用户数为NI i＝（Ii－Oi）＋＝∑nj＝1Qij，净流出用户数为NOj＝（Oj－I j）＋＝∑ni＝1Qij（其中，X＋＝记租赁点i到租赁点j的距离为d ij，令d ij为一个足够大的数M，使得hii＝0，则求解如下线性规划即可得推荐概率hij：

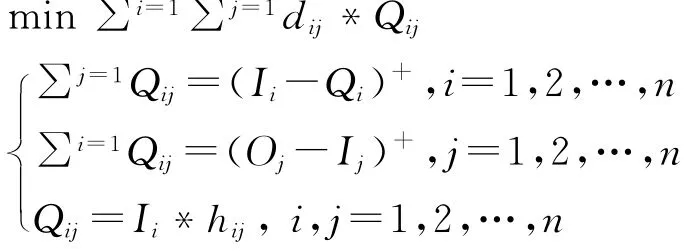
在时间窗t内，对于到达租赁点i还车的用户，按概率将用户推荐至租赁点j。重新计算各租赁点实际的用户借还车需求D′i（t），用D′i（t）代替Di（t），按（1）中方案进行仿真实验。记录总调度数量B。

（3）推荐方案：在推荐方案中，考虑距离等现实因素的限制，推荐的站点距离越远，用户接受推荐的概率越低，当距离超过一定范围后，用户不会再接受推荐。不妨设当距离超过800米后，用户不会再接受推荐方案，令其中Y是一个足够大的数，并令d ii为一个足够大的数Z，且Z小于所有d ij*Y，使得求解（2）中线性规划时，对于距离大于800米的租赁点i、j的推荐概率h ij＝0，当没有满足条件的站点可以推荐时，则不进行推荐，即hij≠0。用d′ij代替d ij，按（2）中策略进行调度，记录总调度数量C。

2．3 实验结果

按上文中的三个方案分别进行计算机仿真实验后所得结果如表1所示。

表1 三个实验方案的调度量对比

由表1可以看出，当采用推荐方案时，如不考虑距离因素，在理想状态下可以使得调度量减少37．77%，即使考虑距离的影响，仅将用户推荐至800米以内的租赁点，也可以使得调度的自行车数量减少8．94%。这一结果虽然相较理想状态下的情况低很多，但这主要是由于公共自行车是短途交通工具，距离较近的租赁点其用户行为也较为相近。当用户数量足够多时，减少8．94%的调度量也可以减少大量调度成本。

表2记录了总调度量最多的30个租赁点在不同方案下的总调度数量，可以看出在理想方案下，调度量较大的租赁点的调度数量下降了50%～70%，可见通过推荐用户到其他租赁点还车的方式，有效降低系统的调度数量。而在推荐方案下，由于距离的限制，虽然不是所有租赁点的调度数量都大幅降低，但是也有约四分之一的租赁点的调度量下降较多，下降了约20%～30%，而其他租赁点的调度量也有一定的改善。由此可见，推荐用户到其他租赁点还车，可以有效减少用户量较大的租赁点的调度量，提高运营效率。

表2 部分租赁点在不同方案下的总调度量

3 总结及展望

综上，本文采用排队论对公共自行车系统的调度问题进行了建模研究，如果以概率将到达租赁点i还车的用户推荐至租赁点j，则当时各租赁点无可用自行车或无空闲车桩的概率最小。基于这一结论我们进行了仿真实验，对无推荐的初始方案、无距离限制的理想推荐方案以及考虑距离因素的合理推荐方案三种情况分别进行了仿真实验，并对比三种方案调度的自行车数量，最终证明通过推荐用户到邻近的站点还车可以有效减少公共自行车系统的调度数量，降低调度成本。

本文主要研究的是各租赁点拥有有限个车桩的公共自行车系统，如果将无桩的共享单车模式看作一个租赁点无穷多、每个租赁点拥有无限个车桩的公共自行车系统，则本文的模型可以拓展至共享单车模式。因此，在后续的研究中，可以对本文的模型进行进一步的扩展。