基于局部最优能耗原理的分汊河道河相关系
张玮,吴彦颖,雷潘
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2.中设设计集团股份有限公司,江苏 南京 210014)
0 引言
冲积平原河流经过长期自动调整,往往会达到平衡或准平衡状态。这种状态下,河道几何形态与水沙条件及河床边界条件存在一定的函数关系,即河相关系。分汊河道具有随外界条件变化而流路调整、主支汊更替的特点,河相关系比单一汊道更为复杂。正确认识分汊河道的河相关系,对分汊河段的治理和维护具有十分重要的意义。
国内外学者曾由分汊河流的平衡条件入手,进行过河相关系研究。早年研究往往针对具体河段展开,诠释河流平衡状态的理论也是林林总总。近年来,不少学者注意到,当分汊河流处于平衡状态时,其分流比与汊道断面面积比之间存在一定的稳定关系。潘庆燊和胡向阳[1]分析长江中下游双分汊河段实测资料发现,各汊分流比与各汊断面面积占汊道总断面面积的比值相近。窦润青等[2]在研究长江口北槽落潮分流比时发现,北槽分流比与北槽和南槽断面流速之比的相关性系数仅是0.441,而与北槽和南槽断面面积之比的相关系数高达0.863,说明河道断面面积对分流比的影响其实比断面流速更大。M.Liang等[3]研究了三角洲地区双分汊河道的矩形河槽概化模型,比较了两汊断面形态的不同对河道水流特性的影响,结果表明,不论河道宽深比是否变化,汊道分流比和河槽断面面积之比具有一定的比例关系。吴志刚等[4]对长江潮汐径流交汇区的如皋沙河段实测数据进行了研究,发现如皋沙河段汊道断面面积与分流比密切相关。不仅如此,当汊道受护岸工程影响,断面面积减小之后,在稳定的分流比条件下,河道横断面能冲刷调整,使断面面积与分流比重新具有良好的相关性。孙志林等[5]基于分汊前后水流挟沙能力相同的假设,推导得到了分汊前后断面面积之比和汊道分流比的指数关系,由此建立平衡水深理论,并以实测资料对该理论进行了验证。以上研究均指出了分汊河段汊道断面面积比与分流比存在着一定的关系,但在以往的研究中,这种关系或是基于简单的归纳总结,缺乏深入的理论探讨,或是基于平衡状态下的水沙运动特征研究,在研究方法上较为单一。
本文从局部最优能耗原理出发,将其从以往的单一河道推广应用于分汊河道,据此推导出双分汊河道分流比与汊道断面面积比和宽深比之间的河相关系公式,利用长江下游东流水道实测资料对其进行验证。在此基础上,对公式进行进一步简化,并利用长江下游多个分汊河段资料验证简化公式的合理性,此外,还将本文公式与现有类似公式进行比较。
1 公式推导
1.1 局部最优能耗原理
极值假说已在河床演变学中得到普遍应用,以γQJ=min的形式为代表的最小能耗原理认为,封闭的动态平衡系统在给定初始和边界条件下,系统整体的能量耗散率将调整至最小。然而,研究表明,河流系统的全局能耗最小一般无法达到,河流极有可能在自我调整中趋于局部最优能耗状态[6]——河床单位面积能量耗散率处处相等,即单位面积能耗率Pa=const。基于局部最优能耗理论,Molnár P 和 Ramírez J A[7]对美国密西西比州Panola County的Goodwin河道试验集水区数据进行了水力几何形态关于流量的分析研究,得出了河相关系中河宽指数和水深指数的最优区间,证明了用局部最优能耗理论解释河流的调整和发展是合理的。不过,局部最优能耗原理目前主要用于研究单一河段的河床形态。对于分汊河道,在达到平衡或准平衡状态后,也应当符合局部最优能耗的条件。因此,本文将局部最优能耗原理推广应用于分汊型河道,也就是说,通过能耗原理获得分汊河道的平衡状态方程。
对于一处平衡或准平衡状态的河流系统,取一段分汊河道,总能量耗散率为:

式中:L为计算河段长度;χ为计算河段湿周;τ0为边界层切应力,在均匀流中τ0=γRJ,水力半径R=;v为断面平均流速,v=。
单位河床面积能量耗散率为:

因为河床单位面积能耗率在河流系统中处处相等,分汊前后Pa=const,故

式中:下标i代表第i汊道;下标0代表分流前的主河道。
式(3)即局部能耗最优时,分流后汊道与分流前主河道所需满足的关系式,该公式也与朗拜恩在分析水流功率沿程分配时提到的一种可能性相符[8]。
1.2 河相关系公式推导
分汊河道分流比为:

水流阻力公式选取曼宁公式:

假设分流前后河道糙率不变,即ni=n0,则

根据最优局部能耗原理式(3)和汊道分流比表达式(4),可得关系式:

冲积河流的河道宽深比反映河道内部特性,选用阿尔图宁基本河相关系式:

式中:指数m在冲积平原的变化不大[9],通常可取 0.75~0.85。
联立公式(3)、(6)、(7)和(8),得到分流前后分流比、河道平均断面面积比和平均宽深比的关系式:


式中:A取过水断面的平均面积;ζ取平均宽深比。
2 公式验证
2.1 验证资料
东流水道位于长江下游九江市至安庆市之间,上起华阳河口,下迄吉阳矶,全长31 km,属顺直分汊河型,是长江下游重点浅险水道之一。东流水道滩群前后分别有老虎滩和玉带洲两大江心洲,水流先自雷港口至老虎岗进入分汊展宽段,由老虎滩将水道分为南北两汊,北汊为老虎滩北槽,南汊为东港。其中,老虎滩北槽经娘娘树后又由玉带洲分莲花洲港于北,西港于南。西港与东港于老虎滩滩尾汇流,并入玉带洲右汊后于玉带洲洲尾与莲花洲港汇流。东流水道具有较为复杂的分流格局,但老虎滩和玉带洲经过长期发展已经形成较稳定的上下滩群构造,可在分析河相关系时不去关注复杂分流、汇流的水流结构,而将分汊河段视为老虎滩双分汊和玉带洲双分汊综合的整体,对河道中段稳定的断面几何形态进行研究。
对于长江中下游来说,航道整治主要关注中枯水期,此时的河道特征是由造床能力较强、且持续时间较长的流量所决定。长江大通站多年平均流量为28 206 m3/s,以此作为参考,选择长江下游2010年、2013年和2017年实测流量分别为38 830 m3/s、23 700 m3/s和 29 985 m3/s的资料对所推导的公式进行验证,各年份分流比情况见表1。

表1 东流水道实测分流比(1985国家高程基准)Table 1 The measured discharge ratio data of Dongliu waterway(1985 national vertical datum)
选取东流水道分汊前河段、老虎滩北槽、东港、莲花洲港及玉带洲右汊作为研究汊段,在各汊道截取足够多的断面,见图1。统计各河段的平均断面面积A、平均河宽,计算平均水深和平均宽深比ζ,列于表2。其中,宽深比系数ζ=。东流水道位于冲积平原,m取值0.75。
2.2 公式验证和分析
根据表2结果,分别计算过水断面比、宽深比、实测面积比和理论面积比(也就是由河相关系计算所得结果),计算结果列于表3和表4,理论值与实测值的相关程度如图2和图3所示。计算结果表明:

图1 东流水道计算断面图Fig.1 Layout of cross sections of Dongliu waterway

表2 各汊平均断面面积、平均宽深比计算结果Table 2 The computational results of mean cross-sectional area and mean width-depth ratio in each channel
1)主河道与各汊道的河相关系相关程度高。在式(9)中,A0是分汊前主河道的平均断面面积。总体而言,根据式(9)计算的理论过水断面比与实测数据吻合较好,相关程度高,相关系数可达0.957 3。就计算误差来说,除了2013年东港水道的误差较大,约为30%以外,其余基本在12%以内,总体精度相对较高,表明所推导的河相关系公式是正确的,同时也说明,局部最优能耗原理可以用来描述处于平衡状态或者准平衡状态下主河道与汊道之间的相互关系。
2)各支汊之间的河相关系相关程度同样也很高。公式(10)主要表示各汊道之间的河相关系,由该式计算所得各流量下面积比的理论值与实测值吻合也较好,两者间的相关程度高,相关系数可达0.966 1。同样,2013年东港水道和老虎滩北槽的误差最大,最大可达27.7~38.3%。除此以外,误差均在可接受范围内。各汊道之间极高的相关系数,说明局部最优能耗原理同样可以用来描述处于平衡状态或者准平衡状态下各汊道之间的相互关系。

表3 式(9)验证结果(Ai/A0)Table 3Verification results of expression(9)(Ai/A0)

表4 式(10)验证结果Table 4 Verification results of expression(10)

图 2 式(9)验证结果(Ai/A0)Fig.2Verification results of expression(9)(Ai/A0)

图 3 式(10)验证结果(Ai/Aj)Fig.3Verification results of expression(10)(Ai/Aj)
至于2013年东港水道误差最大产生的原因,经过分析认为:1)2013年施测流量时,东港的分流比偏大。2013年大通站年均流量为25 000 m3/s,所采用的施测流量为23 700 m3/s,接近或者略小于当年的年均流量。根据现有实测资料,在年均流量附近,东港的分流比一般在27%~33%左右,但2013年的东港水道分流比高达42.5%,明显偏大;2)东港水下地形仍然在冲刷变化之中,尚未达到平衡状态。从东流水道一期航道整治工程竣工到2013年,老虎滩北槽逐年呈淤积态势,特别是2012—2013年淤积有加快趋势,有将汊道水流逼入东港的现象。此外,2013年在老虎滩北缘实施了东流水道二期整治工程的护滩工程,由于工程实施较短,东港水下地形需要一定时间进行调整,尚未达到平衡状态,所以仍然处于冲刷变化之中。
考虑到长江下游分汊河道大多沿干流间隔分布,相邻两个分汊河段间单一河道较长,分流前主河道A0的取值有一定的随意性。因此,为排除计算A0时的主观因素影响,不妨采用分汊河段各汊道断面面积之和∑A来代替A0,见表5,可见两者的结果是十分相近的。采用各汊道断面面积之和的计算结果见表6,并绘于图4。
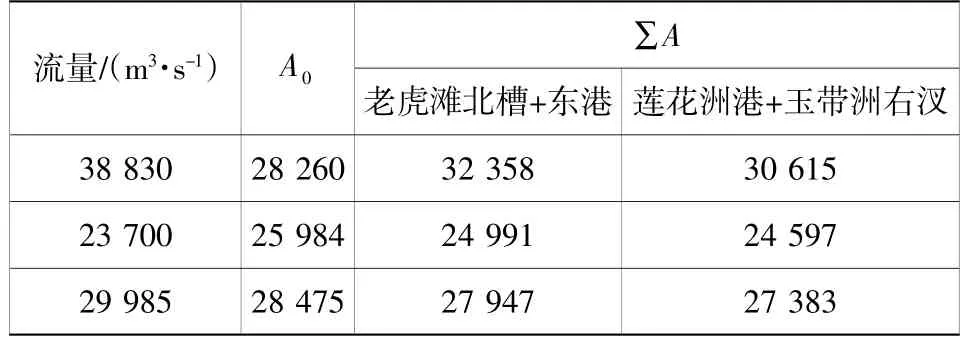
表5 总过水断面面积表Table 5 Total cross-sectional discharge area m2

表6 式(9)验证结果(Ai/∑A)Table 6Verification results of expression(9)(Ai/∑A)

图4 汊道断面面积之和计算结果(Ai/∑A)Fig.4 Verification results calculated by the sum of cross-sectional areas of each branch(Ai/∑A)
相比较而言,无论是计算精度,还是相关系数,都有一定程度的提高,最大误差由30.31%减少到25.33%,相关系数也由0.957 3提高到0.977 3,说明这种做法是切实可行的。
3 河相关系公式的简化
3.1 公式的简化
现有资料表明,指数m的取值范围在0.5~1.0,如华北六条游荡性河流为0.85,俞俊给出中、美、苏60条冲积河流为0.81,明宗富得到冲积河流指数为0.78~0.79[10],周志德得到悬移质输沙(为主河段)为0.837[8]。对冲积河流而言,m的取值范围可以认为在0.75~0.85之间。对于东流水道,当选取m=0.75时,由表3的计算结果可以看出,宽深比项的数值范围为0.96~1.02,接近于1,表明宽深比的变化对于以分流比和断面面积比为主导的河相关系影响相对较小。为此,不妨将公式中的宽深比项略去,由此可得简化的分流比和河道断面面积比的指数公式:

3.2 简化公式的验证
同样,可选取东流水道的实测数据对简化公式进行验证。此外,为更具一般性,拟引用长江下游多个分汊河段的资料对简化公式进行验证。长江南京以下河段的和畅洲、落成洲和福姜沙水道位于长江下游感潮河段。对于感潮河段,落潮流对分汊河道的河床演变产生主要影响[11],且年平均落潮流量与造床流量较为接近。故本文引用长江南京以下12.5 m深水航道工程实践与创新报告中的部分数据,以报告中多年平均落潮流量计算分流比,并由平均潮位以下的河道断面面积计算面积比,计算结果见图5。

图5 简化公式(11)的验证结果Fig.5 Verification results of expression(11)
由图5可以看出,各分汊河段的实测断面比与根据分流比按简化公式计算的断面比吻合较好,说明简化公式能够正确描述分汊河道的河相关系。
4 公式比较
文献[5]曾基于输沙能力相等的原则,对处于平衡或者准平衡状态下的分汊河道,推导出如下河相关系式:

公式(12)与本文的简化公式(11)结构相似,其不同之处在于,在推导过程中,文献[5]采用的是分汊前后挟沙能力相同的假设,而本文采用的是局部最优能耗原理。
为将这两个公式进行比较,仍取与上一节相同的东流水道、和畅洲、落成洲和福姜沙河段资料进行计算,所得结果绘于图6。从图6中可以看到,两个公式的计算结果相近,且均与资料数据吻合较好,相关系数超过0.98。由此可以看出,尽管公式(11)和公式(12)是基于不同的物理学原理推导而得,但其结果相近,都可以得到能够令人满意的汊道河相关系,具有殊途同归的特点。

图6 本文公式与文献[5]中公式计算结果比较Fig.6 Comparison of computational results of formulas in expression(11)and reference[5]
5 结语
1)冲积平原河流经过长期自动调整,往往会达到平衡或准平衡状态,局部最优能耗原理能够用来描述这种水流泥沙以及河床边界之间长期作用的内在联系,也就是河相关系,既适合单一河段,也适合分汊河段。
2)基于局部最优能耗原理,推导出分汊河道分流比与汊道断面面积比和宽深比之间的河相关系公式,经过长江下游东流水道实测资料的验证,结果令人满意,证明所推导公式是合理正确的。
3)进行公式验证时,分别就分汊前主河道与各汊道之间、各个汊道之间等情形,进行了计算比较,结果表明:局部最优能耗原理,不仅适用于主河道与汊道之间,也适用于汊道与汊道之间。
4)考虑到长江下游分汊河道大多沿干流间隔分布,相邻两个汊道间单一河道较长,为排除分汊前主河道断面面积计算时的主观性,不妨采用各汊道断面面积之和来替代分汊前主河道断面面积,结果表明,无论是计算精度还是相关系数都有所提高,说明这种做法是切实可行的。
5)对于所推导的河相关系公式进一步分析发现,其中的宽深比项近似于1.0,可以将其省略,由此得到简化的分汊河道分流比与断面面积比之间的河相关系,经长江下游多个分汊河段实测资料验证,说明简化公式是合理正确的。
6)除此之外,还将本文的简化公式与已有的相近公式进行了比较,结果吻合很好,由此可见,尽管推导公式时所依据的物理原理有所不同,但所得结果相近,具有殊途同归的特点。

