四个分式不等式猜想的解决
广东省广雅中学 (510160)
杨志明
文[1]提出了如下四个猜想:
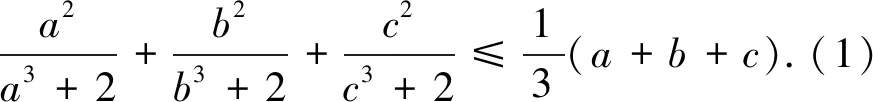



经探讨发现,猜想1-3成立,猜想4不成立.
先否定猜想4.
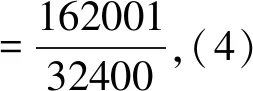
下证猜想1成立.
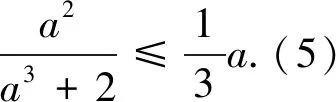
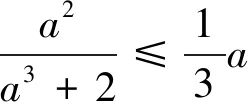
以上三式相加即得(1)式.
从上述证明不难看出,条件abc=1是多余的.
接着证明猜想2成立.
由(6)式知,要证明(2)式成立,只需要证明
4[a(2a+c)+b(2b+a)+c(2c+b)]2≥3[(2a+c)2(b+c2)+(2b+a)2(c+a2)+(2c+b)2(a+b2)].(7)
⟺4[2(a2+b2+c2)+ab+bc+ca]2≥3[(2a+c)2(b(a+b+c)+c2)+(2b+a)2(c(a+b+c)+a2)+(2c+b)2(a(a+b+c)+b2)].(8)
⟺13(a4+b4+c4)+13(ab3+bc3+ca3)-8(a3b+b3c+c3a)+9(a2b2+b2c2+c2a2)-27abc(a+b+c)≥0.(9)
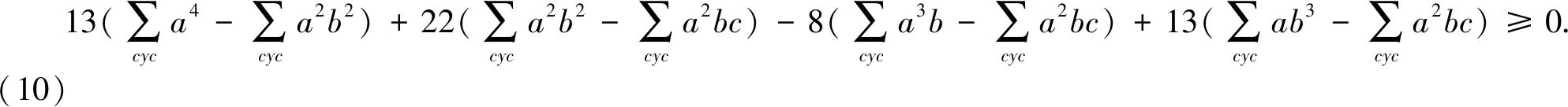
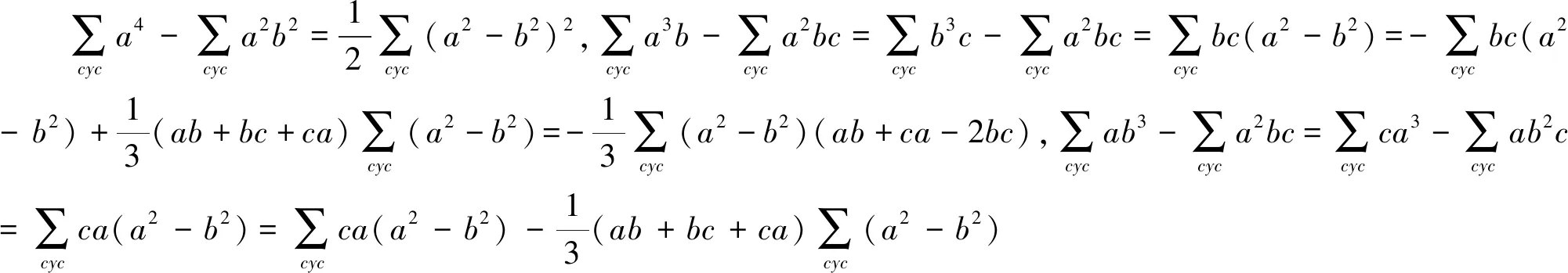
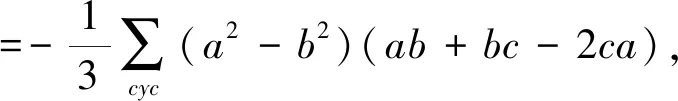
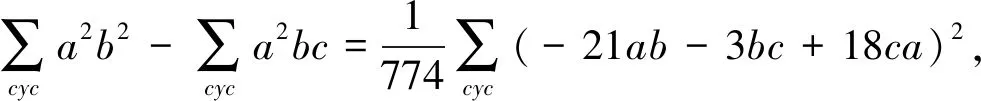
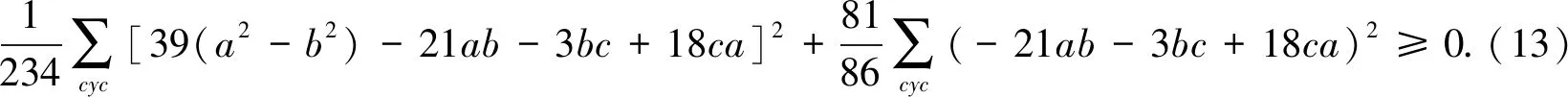
因此,原不等式成立.
最后证明猜想3成立.
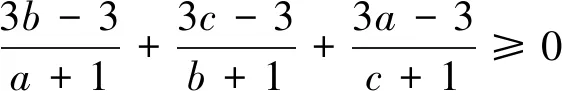
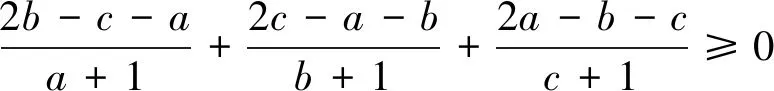
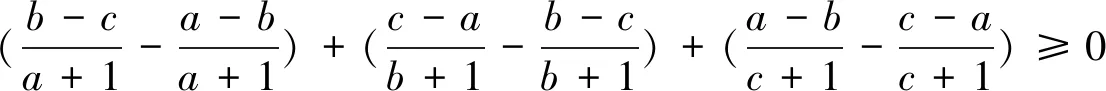
注意到2(a-b)(a-c)=(a-b)2+(c-a)2-(b-c)2,2(b-c)(b-a)=(a-b)2+(b-c)2-(c-a)2,2(c-a)(c-b)=(b-c)2+(c-a)2-(a-b)2,(15)式等价于(b+c+1-a)(a-b)2+(c+a+1-b)(b-c)2+(a+b+1-c)(c-a)2≥0.(16)⟺(2b+2c-a)(a-b)2+(2c+2a-b)(b-c)2+(2a+2b-c)(c-a)2≥0.(17)
由于(17)式是关于a,b,c的轮换对称式,不妨设a=max{a,b,c}.
若a≥b≥c,则(c-a)2≥(a-b)2,2c+2a-b≥0,2a+2b-c≥0,(2b+2c-a)(a-b)2+(2c+2a-b)(b-c)2+(2a+2b-c)(c-a)2≥(2b+2c-a)(a-b)2+(2a+2b-c)(c-a)2≥(2b+2c-a)(a-b)2+(2a+2b-c)(a-b)2=(2b+c+a)(a-b)2≥0.
若a≥c≥b,则2c+2a-b≥0,2a+2b-c≥0.
(ⅰ)若2b+2c-a≥0,则(17)式显然成立.
(ⅱ)若2b+2c-a≤0,则(a-b)2=[(a-c)+(c-b)]2≤2(c-a)2+2(b-c)2.
(2b+2c-a)(a-b)2+(2c+2a-b)(b-c)2+(2a+2b-c)(c-a)2≥(2b+2c-a)[(b-c)2+(c-a)2]+(2c+2a-b)(b-c)2+(2a+2b-c)(c-a)2=3(2c+b)(b-c)2+3(2b+c)(c-a)2≥0.
综上可知,(17)式成立.

