2018年天津卷理科第8题的多解与变式*
四川内江师范学院数学与信息科学学院 (641112)
张 庆 胡 琳 刘成龙
一、试题及简评
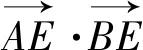

图1
简评:8题是考查向量和平面几何交汇性的典型案例,具有一定难度、深度、广度,呈现一系列亮点:构思巧妙,内涵丰富,解法多样,富有探究性,对学生数学建模、逻辑推理等数学素养要求较高.总之,该试题是测评的好试题、研究的好问题.
二、试题的解法
视角一:模型化
数学模型是研究者依据研究目的,将所研究客观事物的过程和现象的主要特征、主要关系,采用形式化的数学语言,概括或近似地表达出来的一种结构.[1]8题利用极化恒等式模型来解答直观形象,不仅可以缩短思维过程,而且可以优化运算,分析如下:

图2

图3


评注:利用极化恒等式将向量的问题转化成求线段长的平面几何问题,这对于初中学习水平一般的学生来说都能给出正确解答.
视角二:解析法
解析法使得原先独立的两个数学分支—几何和代数联系到一起,使得代数的很多对象有了直观的几何解释.同时,利用代数和分析的知识能较方便地解决几何问题.[2]解析法是利用代数方法解决几何问题的常规解法,难度低,易操作.

图4

评注:利用解析法解答时,将几何问题转化成了代数问题,降低了问题的思维难度.顺便指出,建系的方法很多,比如:以点A为坐标原点,DA、DC分别为x、y轴.
视角三:向量的基本运算
合理利用向量的分解来进行向量间的基本运算,可将向量的数量积转化为关于单个向量的表达式.
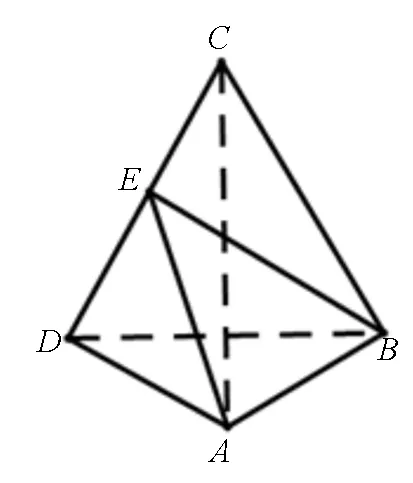
图5


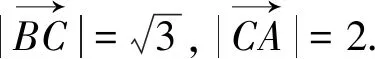
评注:方法4、5通过向量的基本运算将数量积转化为了关于某个变量的二次函数的最值问题,这与方法3有异曲同工之妙.
视角4:利用余弦定理

评注:解法6利用余弦定理将数量积关系最终转化为二次函数最值问题,与方法3、4、5在落脚点上一致.
三、问题的变式
变式是指相对于某种范式,不断变更问题情境或改变思维角度,使事物的非本质属性时隐时现,而事物的本质属性保持不变的变化方式.8题可以从多角度进行变式,如下:
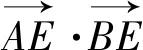

评注:变式1、2立足点是第8题的解答方法.
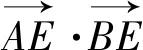
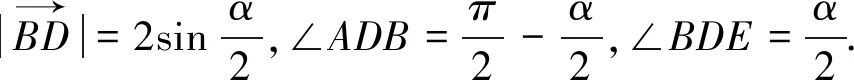
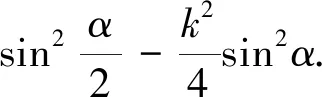
评注:变式3是第8题的一个推广.从第8题到变式3体现了特殊到一般的研究方法.

