零耦合度且部分解耦的3T1R并联机构设计与运动分析
沈惠平 许正骁 许 可 邓嘉鸣 杨廷力
(常州大学现代机构学研究中心, 常州 213016)
0 引言
具有空间三平移一转动(3T1R)功能的并联机器人操作手,其工作空间大、速度快、刚度高,在现代制造业中有着良好的应用前景。但是,一般这类少自由度并联机构结构复杂、耦合度高、运动输入-输出不解耦,且易出现奇异位置,因此,4自由度3T1R并联机构新机型的设计和性能研究一直受到国内外学者的关注。文献[1-3]设计了H4、I4、Par4等系列的4自由度3T1R并联操作手;赵铁石等[4]提出了一种4-URU型3T1R并联机器人;金琼等[5]基于单开链(Single-open-chain,SOC)方法,提出了一类3T1R并联机器人;KONG等[6]基于螺旋理论,通过构建能产生3T1R运动的支链,综合出一组具有相同支链的并联机构;RICHARD等[7]对一种部分解耦的4自由度3T1R并联机构进行了运动学分析;CORBEL等[8]对3T1R并联机械手的加速度特性进行了研究;AMINE等[9]对具有相同支链的3T1R并联机构的奇异性条件进行了研究;黄田等[10]在H4、I4、Par4等相似机器人主体构造的基础上,发明了一种3T1R的Cross-Ⅳ型高速搬运机器人,并实现了产业化;刘辛军等[11]研发了X4机器人;文献[12-13]对含有4条相同支链的3T1R并联机构进行了分析。但上述3T1R机构大部分耦合度κ大(κ≥2),且运动不解耦,给运动控制及轨迹规划带来了困难。文献[14]提出了一种低耦合度且运动解耦的3T1R并联操作手,但因其耦合度κ=1,位置正解仍无法求得其解析解,给误差分析、实时控制等带来了困难。
本文提出一种零耦合度且具有部分运动解耦性的3T1R并联机器人机构,并对此机构的拓扑特性(POC集、自由度、耦合度、运动耦合性)以及运动学(位置正逆解求解、工作空间与转动能力、奇异位置,以及速度、加速度)特性进行系统分析。
1 3T1R并联机构设计及拓扑分析
1.1 机构设计
根据基于POC方程的并联机构拓扑结构设计理论[15-16]、并联机构结构降耦原理[17],以及冗余支链消除奇异位置的原理[18-19]可知:需具有零耦合度(κ=0),即要求有部分支链回路的约束度为零;需具有运动部分解耦性,即要求包含两个以上至少各含一个驱动副的基本运动链(BKC);冗余支链消除奇异位置,即需要根据POC集和自由度,对支链在动静平台之间作特殊布置。根据这些分析,本文提出一种含冗余支链的零耦合度且具有部分运动解耦的4-DOF 3T1R并联机器人机构,如图1所示。
(1)该机构包括含平行四边形的一条混合支链(Hybrid single-open-chain,HSOC1),包含4个分支链A、B、C、D,其中,由4个球副组成的平行四边形(◇S1S2S3S4),其一短边杆3与驱动杆2固接后,再用转动副R11与静平台0连接,为支链A,记作RPa(4S);另一短边杆5的右侧延伸端,与三平行轴线转动副组(R21‖R22‖R23)(记支链B)并联连接;短边杆5的左侧延伸端,与另一三平行轴线转动副组(R51‖R52‖R53)(记支链C),也并联连接,这样,支链A与B(或A与C)构成一个子并联机构,记作:RPa(4S)3R(3R表示支链B或C的3个转动副);同时,短边杆5的上侧通过与其固接的杆8,与杆9两平行轴线转动副组(R12‖R13)(记支链D)串联连接,但R12⊥R23。
1.2节将说明:该混合支链中的子并联机构(RPa(4S)3R)的子平台输出杆5将产生两平移的输出;而整个混合支链的末端(即动平台1的一部分)将产生三平移一转动(绕R13)的输出。
(2)另外,无约束支链SOC2{R31-S32-S33}铰接于SOC3{R41-S42-S43}的球副S43处,从而构成第2条HSOC2,因此,机构动平台1只有两个联接点,即R13和S33。
静平台0上的各转动副轴线的布置关系为:R11⊥R21,R21‖R51;而R21与R31,R41与R51轴线分别重合。1.2节将证明输出杆5两侧的任一支链B、C为冗余支链,设支链C为冗余支链。因此,可取转动副R51为冗余驱动副:机构正常工作时,该冗余支链处于被动、随动状态;当机构出现奇异时,该冗余驱动副R51产生动作,以消除机构奇异位置。
1.2 机构的拓扑分析
1.2.1机构的方位特征(POC)
由文献[15-16]可知,串联、并联机构的POC集方程分别为
(1)

(2)
式中m——运动副数v——独立回路数
MJi——第i个运动副的POC集
Mbj——第j条支链末端的POC集
MPa——机构动平台的POC集
选动平台1上任意一点O′为基点,由1.1节可知,HSOC1包含A、B、C、D 4个支链,其构成分别为RPa(4S)(支链A)、R21‖R22‖R23(支链B)、R51‖R52‖R53(支链C),以及R12‖R13(支链D)。因此,由式(1)、(2)可得
MHSOC1=(MA∩MB∩MC)∪MD
由式(1)可得



由式(2)可得
(3)
由式(3)可知,因支链A、B构成一子并联机构,其输出杆5已得到两平移零转动(2T0R)的输出,且支链C与支链B的拓扑结构和POC集完全相同,支链C对支链A、B构成的子并联机构的POC集没有影响,因此,它已属于冗余支链。
由式(1)可得
Mb1=MHSOC1=M(A-B)∪MD=
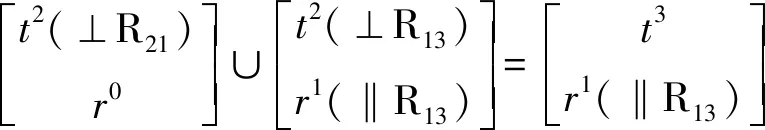
HSOC2末端的POC集为
由式(2)可得机构的POC集为
因此,当静平台0上的4个转动副R11、R21和R31、R41为主动副时,动平台1即产生3个移动和1个转动(绕转动副R13的轴线)的输出运动。
1.2.2自由度
并联机构全周DOF一般公式[12]为
(4)

(5)
式中F——机构自由度
fi——第i个运动副的自由度
ξLj——第j个独立回路的独立位移方程数
dim.——方位特征集的维数

Mb(j+1)——第j+1条支链末端构件的POC集
由支链A、B组成的第1个回路,即RPa(4S)3R由式(5)知其独立位移方程数为
由第1回路组成的第1个子并联机构Sub-PM的DOF和POC集,由式(4)可得
F(A-B)=∑f-ξL1=(5+3)-6=2
由式(3)可得
如图2所示,因球副S32和S42间的距离是变化的,故在球副S32和S42间设想存在一个虚拟的移动副P(此时,可把球副S32、S42、S43的组成体,视为一个整体三角形构件)。这样,由{R31-S32-P-S42-R41}构成第2个回路,其中,绕球副S32和S42连线的转动自由度,对第2回路的运动位置没有影响,但对第3回路的运动位置有影响,故应将其放入第3回路中考虑。由式(5)易知,第2回路的独立位移方程数为
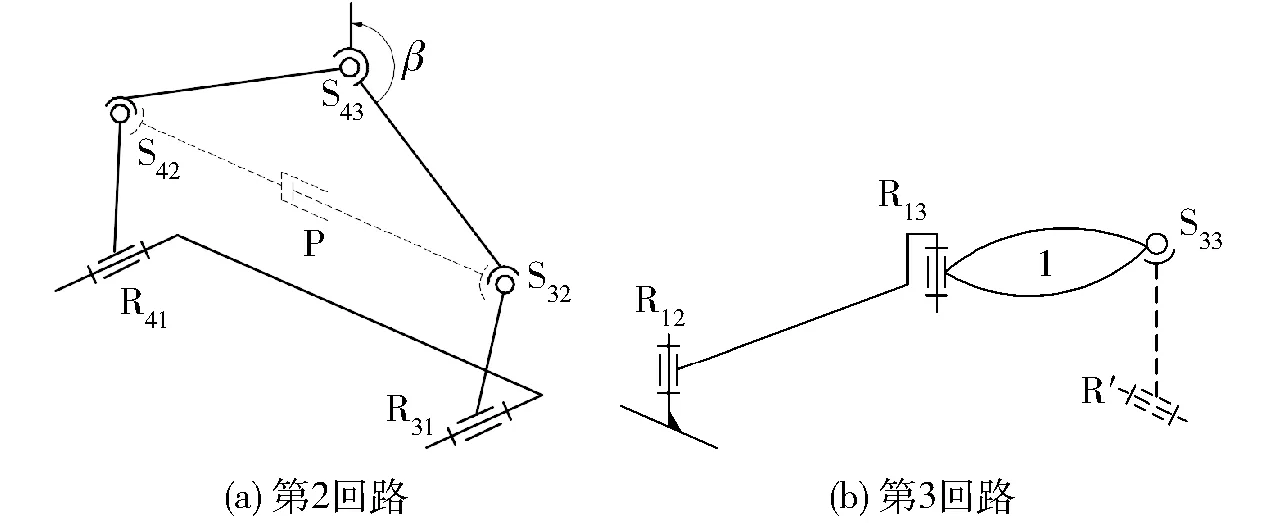
图2 第2、3回路的构成Fig.2 Composition of the second and third loops
由式(4)可得第2回路组成的第2个子并联机构Sub-PM的DOF为
FL2=∑f-ξL2=(9-1)-6=2
因球副S32、S42、S43组成的整体三角形构件绕球副S32和S42连线的转动,等效为一个转动副R′,所以第3回路的组成为{R12-R13-S33-R′},由式(5)可得
由式(4)可得整个并联机构的DOF为
1.2.3机构耦合度
由基于单开链(SOC)单元的机构组成原理[15-16]可知,任一机构可分解为一系列单开链,第j个单开链(SOCj)的约束度为
(6)
式中mj——第j个SOCj的运动副数
Ij——第j个SOCj的驱动副数
一组有序的v个SOC可构成一个独立回路数为v的基本运动链(Basic kinematics chain,BKC),对一个BKC则有
因此,耦合度为
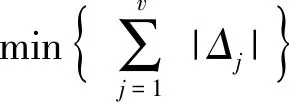
κ揭示了机构基本回路变量之间的关联、依赖程度;κ值越大,机构的运动学、动力学分析越复杂。
前文已计算了上述3个回路的独立位移方程数分别为ξL1=ξL2=ξL3=6,因此,3个回路的约束度均可由式(6)求得:Δ1=8-2-6=0,Δ2=(9-1)-2-6=0,Δ3=6-0-6=0。
上述3个回路均独立构成一个BKC,因此,该机构包含3个BKC,即BKC1、BKC2、BKC3,它们的耦合度分别为κ1=κ2=κ3=0;整个机构的运动位置正解,可依次通过BKC1、BKC2、BKC3直接求出其解析解。
2 位置分析
2.1 基于序单开链的机构位置正解求解原理
由文献[16,20]知,因任一机构可分解为若干个BKC,而每个BKC又可分解出约束度为正值、零、负值3种形式的单开链,因此,机构位置正解的求解,可转换为3种单开链的位置求解,而这3种单开链的约束特性及其建模方法为:

2.2 参数标注
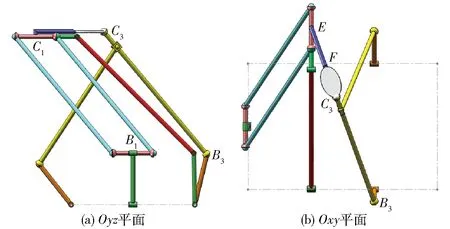
建立图1机构的运动模型,如图3a所示,因冗余支链正常情况下处于随动状态,对机构正常工作不起作用,因此,机构运动学分析时,可不考虑图3a中的冗余支链(即A5-B5-C5支链);同时,为了计算方便,将图1 中的β定为180°,即点B3、C4、C3在一条直线上。
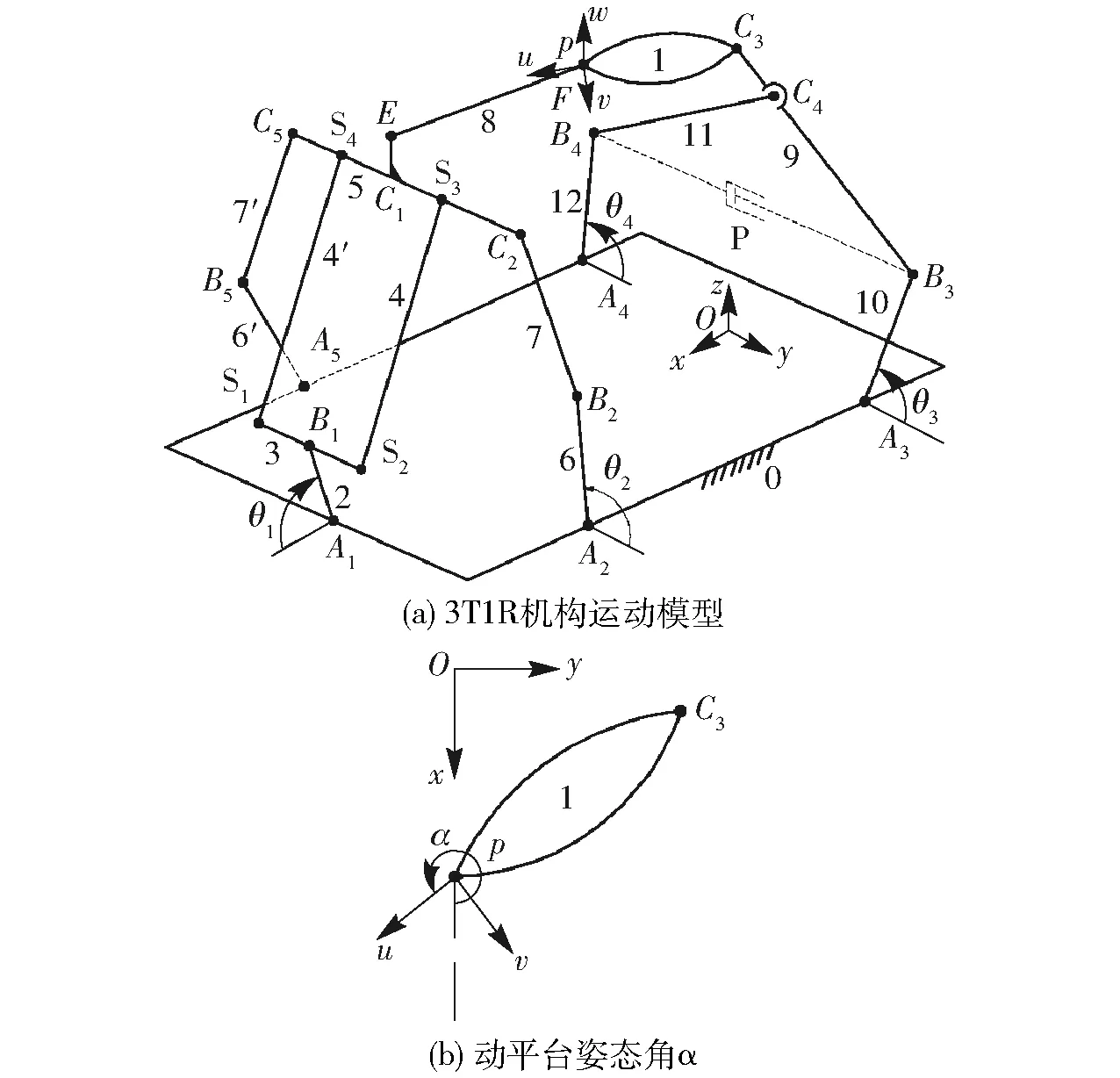
图3 3T1R并联机构的运动建模Fig.3 Kinematic modeling of 3T1R parallel mechanism
设该机构静平台0为矩形,A1、A2、A3、A4分别表示位于静平台0上的转动副R11、R21、R31和R41的位置。
在静平台上建立Oxyz坐标系,坐标系原点O位于A3和A4连线的中点,x轴过A1点,y轴与A3A4重合,z轴由右手法则确定;在动平台1上建立puvw坐标系,原点p位于F点(即动平台1与转动副R13的相连处),u轴平行于FC3连线,w轴与z轴平行,v轴由右手法则确定。
设θ1、θ2、θ3、θ4分别为转动副R11、R21、R31、R41的输入角(θ1为x轴正向与杆2的夹角,θ2、θ3、θ4分别为y轴正向与杆6、10、12的夹角),如图3a所示;动平台1的姿态角α为u轴正向与x轴正向之间的夹角,如图3b所示。
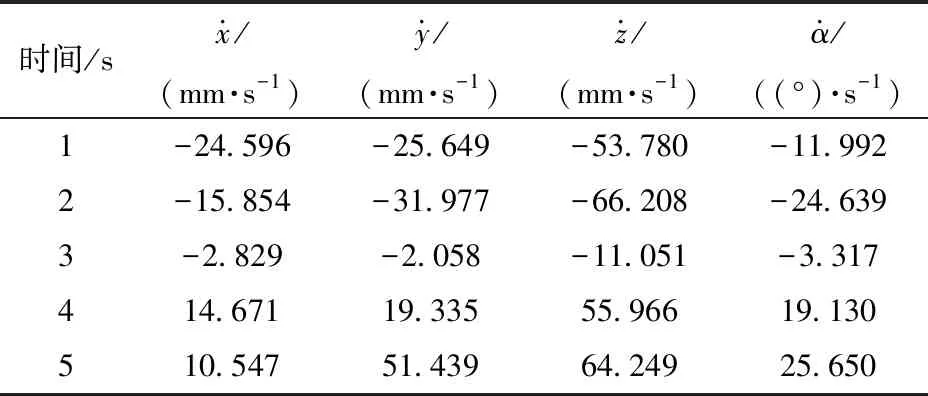
该机构结构参数为:动平台长为FC3=l3,主动杆A1B1=A2B2=A3B3=A4B4=l4( 已知主动输入角θ1、θ2、θ3、θ4,求动平台1上p点的位置(x,y,z)及姿态角α。 2.3.1BKC1的位置求解 求得点B1、B2的坐标分别为:(2l1+l4cosθ1,0,l4sinθ1)、(l1,l2+l4cosθ2,l4sinθ2)。因BKC1的κ1=0,因此,输出杆5上C1点的位置计算如下: 由式(3)可知,输出杆5的输出运动为两平移(2T)且始终平行于yOz平面,因此,xC1=l1,即C2的坐标为(l1,yC1+2l6,zC1)。 由杆长B1C1=B2C2=l5可得约束方程 (7) 并整理得 HyC1+MzC1=N 其中 H=2(yB2-2l6)M=2(zB2-zB1) 若H=M=0,则N=-(xB1-l1)2=0,但由于l4 (1)当H=0时 (2)当H≠0时 其中 2.3.2BKC2的位置求解 在BKC2中,球副S32和S42连线上的任意一点均可作为整个回路的末端点,故只需这两个球副的坐标即可求解连线上任意一点的坐标。 根据主动臂的杆长和输入角θ3、θ4即可求出点B3、B4的坐标分别为(0,l2+l4cosθ3,l4sinθ3)、(0,-l2+l4cosθ4,l4sinθ4)。 2.3.3BKC3的位置求解 在三角形B4C4B3中,由杆长约束B3C4=B4C4=l9可得 (8) 解方程组可得 由于B3、C4、C3在同一杆上,可根据杆长比例求得C3点的坐标为 在E-F-C3中,由杆长约束FC3=l3和EF=l7可得 (9) 解方程组可得 (10) 其中 至此,动平台末端点p的坐标已求得,而转角α可由动平台上p与C3两点的坐标求得,计算公式为 (11) 由式(10)、(11)可知,x=φ(θ1,θ2,θ3,θ4)、y=f(θ1,θ2,θ3,θ4)、z=φ(θ1,θ2)、α=η(θ1,θ2,θ3,θ4),因此,该机构具有输入-输出(I-O)部分运动解耦性。 已知动平台p的坐标(x,y,z)和姿态角α,求输入角θ1、θ2、θ3、θ4。 而C2、C4的坐标分别根据C1、C3的坐标可得 C2=(l1,yC1+2l6,zC1) 由杆长约束B1C1=B2C2=B3C3=l5,B4C4=l9有 (12) 由此可得 (13) 综上,C1点坐标有两组解,且输入角θ1、θ2、θ3、θ4均有两组解,故该机构位置逆解共有32组解。 2.5.1正解算例 设并联机构结构参数为l1=300 mm,l2=300 mm,l3=150 mm,l4=250 mm,l5=800 mm,l6=100 mm,l7=200 mm,l8=25 mm,l9=700 mm。 设4个输入角分别为:θ1=51.45°、θ2=31.81°、θ3=76.61°、θ4=124.57°。 根据位置正解式(10)、(11)求得4组实数正解,如表1所示。 表1 位置正解数值Tab.1 Numerical values of direct kinematics 2.5.2逆解算例 并联机构的工作空间,是指在考虑运动副转角范围(球副转角为±30°)、无奇异及杆长不干涉等约束条件下,末端执行器的工作区域。本文采用极限边界搜索法对该并联机构工作空间进行分析,首先,根据杆长设定工作空间的搜索范围,然后,基于位置逆解式(12)求得该并联机构的工作空间。 图4 工作空间三维图Fig.4 Three dimensional diagram of workspace 确定空间三维搜索范围:600 mm≤z≤1 000 mm,-π≤θ≤π,0≤ρ≤800 mm(略大于杆件的活动范围即可)。通过Matlab软件编程,得到该并联机构的三维工作空间如图4所示;取不同z值时的x-y截面图,如图5所示。 图5 工作空间的x-y截面图Fig.5 x-y sections of workspace 由图4、5可得,在z∈[600 mm,950 mm]范围内,工作空间截面连续,且随着z增加,截面面积逐渐缩小。由于杆5的运动始终垂直于x轴且位于支链B、C所组成的平面内,故动平台上的p点在x方向上的极限位置,只与杆8的杆长l7有关,故工作空间仅在x∈[100 mm,300 mm]上存在。 图6 z=600 mm时x-y截面各点动平台转角的分布Fig.6 Distributions of rotation angles of PM at z=600 mm 转动能力是指动平台(末端执行器)在工作区域内的转角范围,是衡量并联机构输出转动灵活性的重要指标。本文采用与求解工作空间一样的极限边界搜索法,基于逆解式(12)分析某一固定z值处平面内各点的转动能力。现取z=600 mm,通过Matlab,求得该高度z上x-y截面内的转角α的范围,如图6所示。 由图6可知,动平台在z=600 mm时,转角α的范围很大,能达到[-180°,180°]的区域面积为0.23 m2,约占总区域面积(0.33 m2)的70%,表明在该平面内,动平台具有较大的转动能力;在z=700、800 mm的截面内,其对应的数值分别为66%和54%,因此,当动、静平台的距离变大时,动平台的转动能力会逐渐削弱。 当机构处于奇异位置时,运动会出现分岔现象,此时,机构的运动不具有确定性。因此,在并联机构设计时,有必要对其可能存在的奇异位置进行分析。本文通过对位置逆解公式的求导,得出并分析雅可比矩阵,进一步得到该并联机构可能存在的奇异位置。 JpV=Jqω (14) 其中 图7 输入奇异位置Fig.7 Input singularity position 当雅可比矩阵Jp和Jq中,只要有一个矩阵的行列式为零,该机构就会出现奇异位置。据此,可将并联机构的奇异位置分为两类:输入奇异、输出奇异。 4.2.1输入奇异 当det(Jq)=0时,机构发生输入奇异,此时机构的执行构件将失去某个方向的运动能力。一般此时的位形情况是一个运动链达到了工作空间的边界。 由det(Jq)=0得Jq矩阵的行列式解的集合为 W={W1∪W2∪W3∪W4} 当W1=(zB1-zC1)l4cosθ1-(xB1-xC1)l4sinθ1=0,即杆2和平行四边形短边中点连线在Oxz面上的投影共线,如图7a所示。 当W2=(zB2-zC2)l4cosθ2-(yB2-yC2)l4sinθ2=0,即杆6和杆7在Oyz面上的投影共线,在当前的杆长条件下不会出现这种情况。 当W3=(zB3-zC3)l4cosθ3-(yB3-yC3)l4sinθ3=0,即杆10和杆9在Oyz面上的投影共线,如图7b所示。 当W4=(zB4-zC4)l4cosθ4-(yB4-yC4)l4sinθ4=0,即杆12和杆11在Oyz面上的投影共线,如图7c所示。 4.2.2输出奇异 当det(Jp)=0,机构发生输出奇异,此时当所有的主动件锁住时,执行构件依旧可以产生局部运动,从而使输出产生不确定性。 将矩阵Jp看作4个列向量,即 为使det(Jp)=0,有以下3种情况: (1)两个向量线性相关 设ke1=e3(即e1、e3线性相关),此情形可导出3种奇异条件,由式(10)可得: 平行四边形短边中点连线和杆9在Oyz平面上的投影平行,如图8a所示。 当kf11=f31,即 杆9和杆8在Oxy平面上的投影平行,如图8b所示。 当kf14=f34,即 杆9和FC3连线在Oxy平面上的投影平行,如图8b所示。 图8 输出奇异位置(1)Fig.8 Output singularity (1) 两向量线性相关的其他组合分析与此类似,不再一一赘述。 (2)3个向量线性相关 设e3=k1e1+k2e2(k1k2≠0),则有: 平行四边形短边中点连线、杆7和杆9在Oyz平面上的投影不平行,如图9a所示。 当k1f11+k2f21=f31,即 杆9和杆8在Oxy平面上的投影平行,如图9b所示。 当k1f14+k2f24=f34,即 杆9和FC3连线在Oxy平面上的投影平行,如图9b所示。 图9 输出奇异位置(2)Fig.9 Output singularity (2) 其余情况分析过程类似,不再一一赘述。 (3)4个向量线性相关 设e2=k1e1+k2e3+k3e4(k1k2k3≠0),结合前面两种情况的分析,此时,k1、k2、k3的值无法解出,此种情况不存在。 由式(12)的4个方程,可表示成唯一形式f(x,y,z,α)=0,全微分后可得 (15) 对式(15)两边同时除以dt得 (16) 当机构不存在奇异位置时,Jp可逆,则 (17) 式(17)即为动平台原点p的速度正解公式。 取式(15)对时间t求导,可得 (18) 当机构不存在奇异位置时,Jp可逆,则 (19) 式(19)即为动平台原点p的加速度求解公式。 通过Matlab编程计算,得到动平台1的速度与加速度,分别如表2、3所示。 表2 动平台速度Tab.2 Velocity of moving platform 表3 动平台加速度Tab.3 Acceleration of moving platform 同时,将该并联机构的三维模型,通过Solid-Works导入到ADAMS软件中进行仿真,得到动平台的速度与加速度曲线,分别如图10、11所示。 通过对比表2和图10及表3和图11可以得到,运用Matlab对式(15)~(19)进行编程计算得到的数值,与运用ADAMS仿真得到的曲线图基本一致,其相对误差仅为0.1%,例:表2中t=2 s时的数据与图10中对应的4个数值(-15.800,-31.890,-66.215,-24.608)基本一致,从而验证了所推导的速度与加速度公式的正确性。该机构动平台的速度、加速度曲线,变化连续平稳、无突变峰值,具有较好的运动稳定性。 图10 动平台的速度曲线Fig.10 Velocity curves of moving platform 图11 动平台的加速度曲线Fig.11 Acceleration curves of moving platform (1)揭示了该机构的POC、自由度、耦合度、运动耦合性等重要拓扑结构特征,为简化其运动学分析奠定了基础。 (2)根据提出的基于序单开链的运动学建模原理,建立了该机构位置正解的求解模型,求解出了位置正解的解析解。 (3)基于导出的位置逆解公式,对该机构的工作空间和转动能力进行了分析,发现其工作空间连续且转动能力良好。 (4)分析了该机构可能存在的奇异位置及其出现的几何条件,并通过雅可比矩阵推导出该机构动平台的速度、加速度变化规律。2.3 位置正解求解
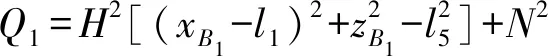


2.4 位置逆解求解
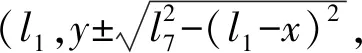
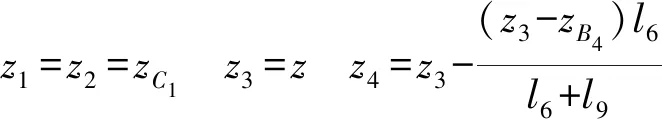
2.5 位置正逆解的实例验算

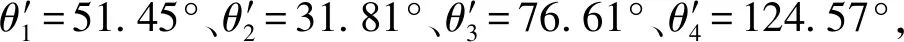
3 工作空间和转动能力
3.1 工作空间
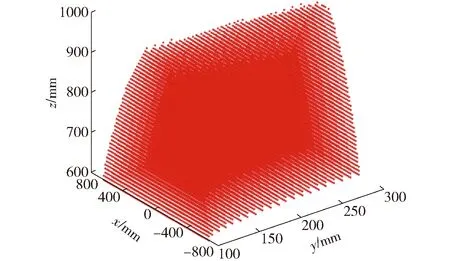
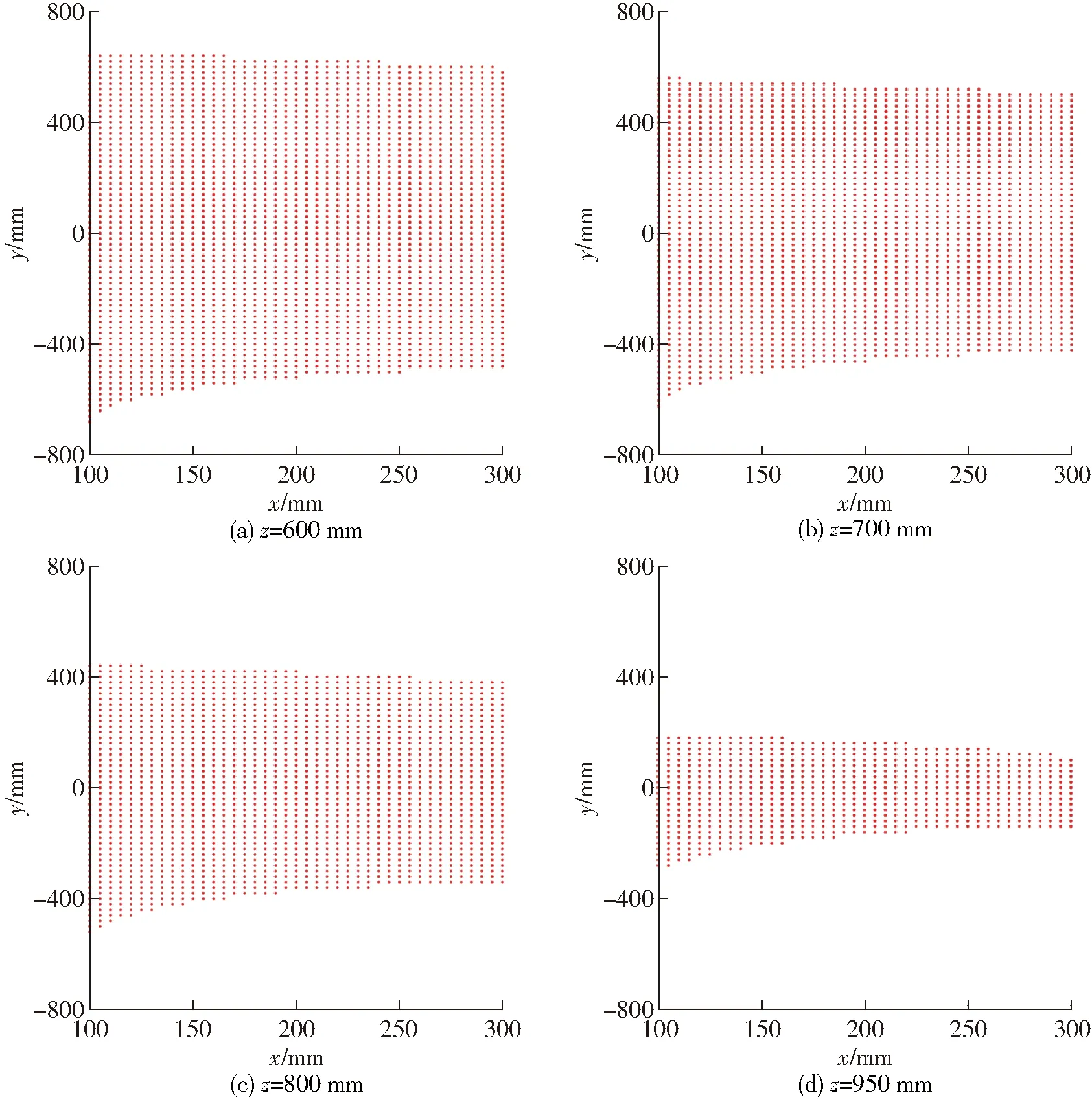
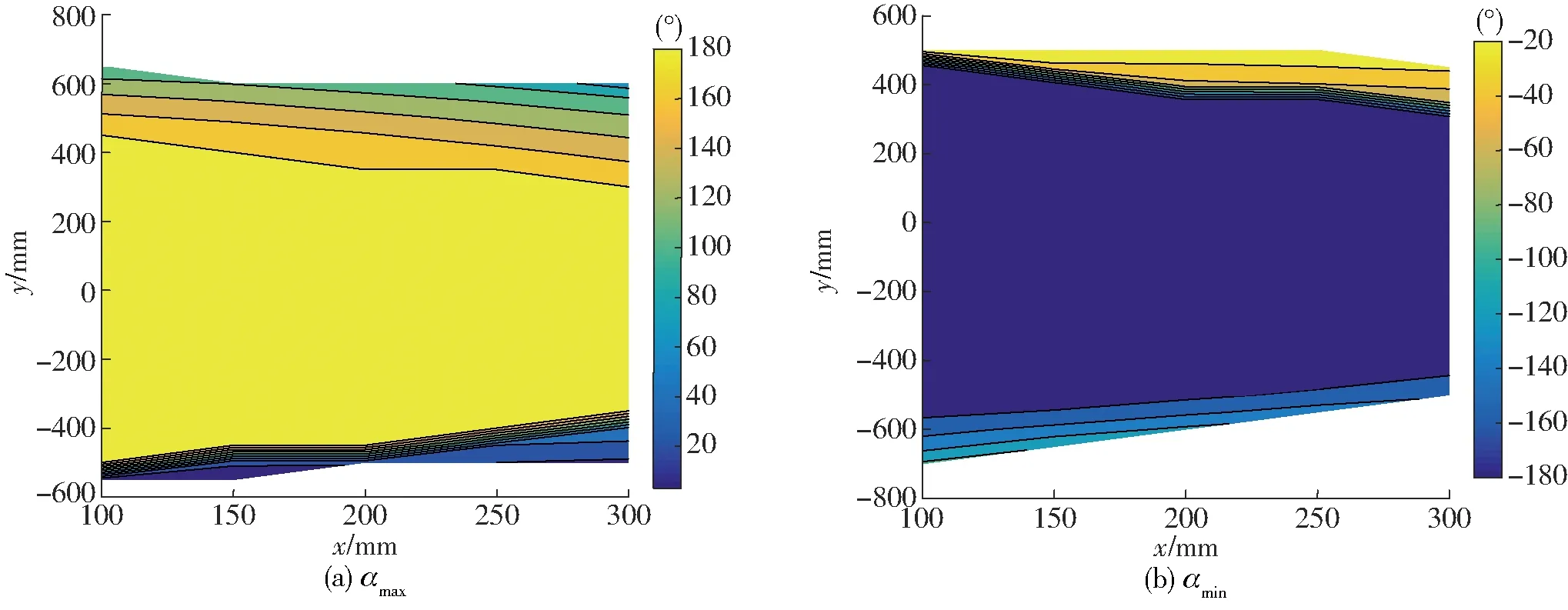
3.2 转动能力
4 奇异位置分析
4.1 雅可比矩阵求解

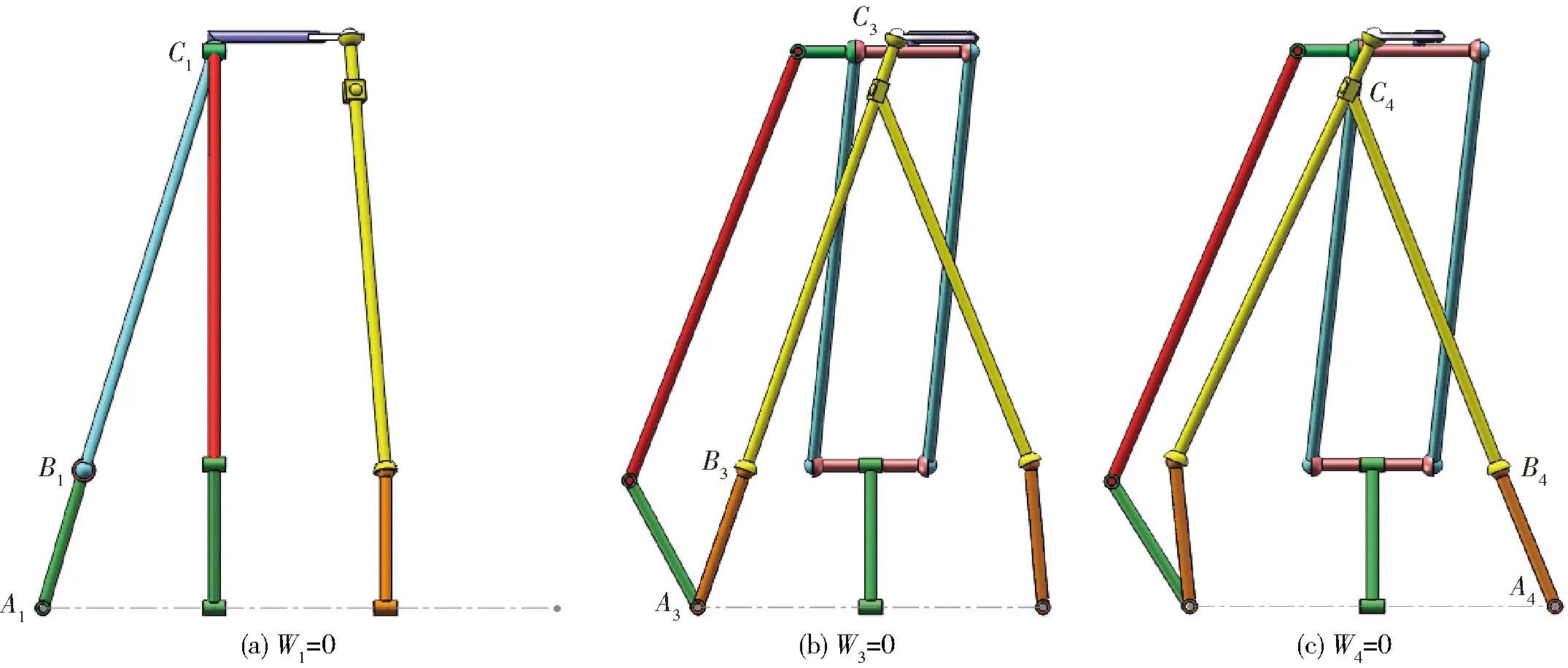
4.2 奇异位置求解


5 速度与加速度
5.1 速度公式

5.2 加速度公式

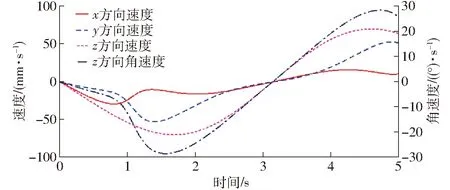
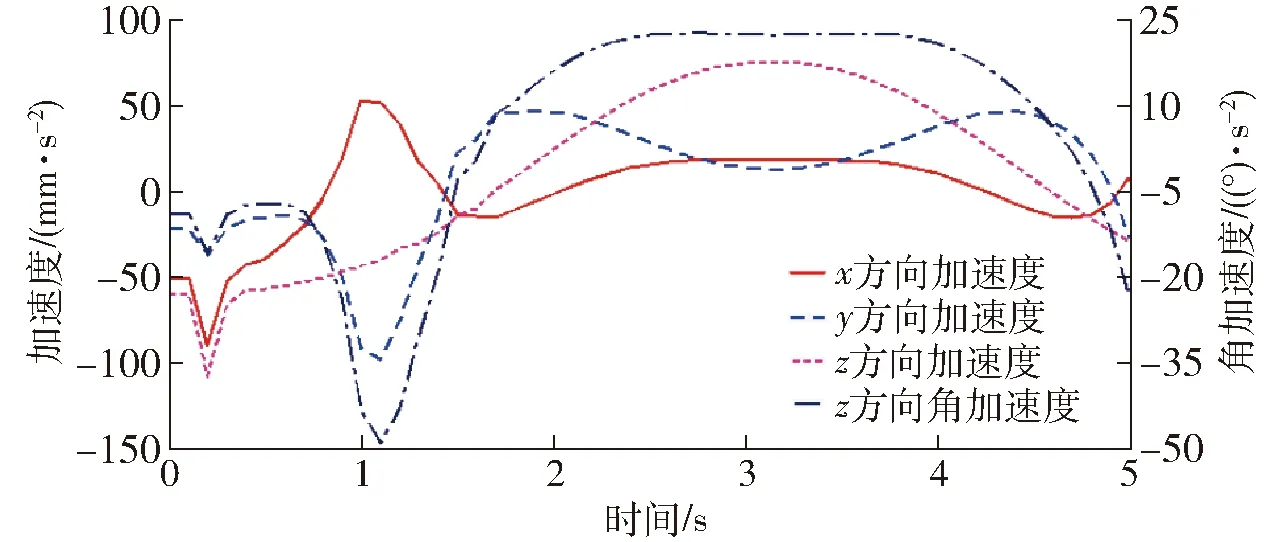
5.3 算例与仿真


6 结论

