基于非线性模型预测控制的农用拖挂车避障控制器研究

白国星 刘 立 孟 宇 罗维东 顾 青 梁 晨

(北京科技大学机械工程学院， 北京 100083)

0 引言

农用机械自动导航控制是实现农业现代化的一项关键技术[1-3]。避障是指移动装备在跟随给定路径时，识别障碍物并完成避障动作[4]，它关系到农用机械自主导航控制的安全性，因而具有十分重要的研究意义。实现避障功能需要两项关键技术，即障碍物检测技术和避障控制技术。关于障碍物检测技术的研究成果颇丰，文献[4]详细介绍了该技术在国内外的研究现状和发展趋势，而关于农用拖挂车等农用机械避障控制的研究正在发展。

农用拖挂车与无人机、乘用车辆等同为移动装备，所以可以参考无人机等领域的避障控制方法。目前在无人机领域存在两种解决方案，其中一种通过在线路径规划算法实现避障控制，另一种则基于模型预测控制(Model predictive control, MPC)方法建立避障控制器。常用于避障控制的路径规划算法有A*算法[5]、神经网络算法[6]、人工势场法[7-8]等，由于路径规划算法通常将移动装备视为质点，未考虑执行器饱和等系统约束，因此移动装备可能无法以较小的误差跟踪规划得到的路径。MPC方法最显著的优势是可以显式地考虑系统的状态约束，基于MPC方法的避障控制器在乘用车、无人机等移动装备的自主导航中已有较为广泛的应用[9-14]。

考虑到农用拖挂车结构[15-18]不同于文献[9-14]中的乘用车和无人机，而不同的结构产生的内轮差也不相同[19]，本文基于刚体运动学和非完整约束条件建立用于避障控制的农用拖挂车运动学模型。在此基础上，提出农用拖挂车的状态预测模型，并基于改进的禁区惩罚函数设计优化目标函数，从而提出基于非线性模型预测控制(Non-linear model predictive control, NMPC)的农用拖挂车避障控制方法。通过Matlab/Simulink对提出的避障控制方法进行仿真验证。

1 运动学模型建立

运动学模型在乘用车等移动装备运动控制中的应用非常广泛[13,20-23]，其理论基础是刚体运动学，假设条件为车体不发生侧向滑动，即车体满足非完整约束条件。农用拖挂车的运动学模型如图1所示，包括拖车和挂车两部分，车身之间通过铰接点连接。

由于拖车的结构与乘用车的结构基本相同，因此拖车的运动学模型可参照文献[13，22]中的乘用车运动学模型

(1)

式中xh、yh——拖车后桥中点的横、纵坐标值

θt——拖车航向角

δ——拖车转向角

vt——拖车纵向行驶速度

lt——拖车轴距

避障控制不仅需要考虑拖车后桥中点的位置和姿态，还需考虑其前桥，参照文献[13]，由式(1)推导得到拖车前桥中点的位置和姿态

(2)

式中xq、yq——拖车前桥中点的横、纵坐标值

式(1)和式(2)即用于乘用车避障控制的运动学模型，即拖车运动学模型。

对于挂车的运动学模型，由于拖车与挂车的铰接点距离拖车的后桥中点较近，因此可视为挂车在铰接点处的速度与拖车后桥中点的速度相同，即

(3)

其中

γ=θt-θg

(4)

式中vg——挂车纵向行驶速度

θg——挂车航向角

γ——铰接角

lg——挂车车桥与铰接点之间的距离

求解式(3)可得

(5)

由于挂车也符合非完整约束

(6)

式中xg、yg——挂车车桥中点横、纵坐标值

求解式(6)可得

(7)

(8)

2 NMPC避障控制器设计

设计NMPC避障控制器包含建立预测模型和设计滚动优化目标函数两部分。预测模型的作用是根据车辆当前的位姿状态和未来可能的控制输入预测未来可能出现的位姿状态，NMPC避障控制器的预测模型可以通过农用拖挂车的运动学模型推导获得。

为了便于表达，式(8)抽象为

(9)

其中

控制器的采样间隔很小，所以可以采用欧拉法(Euler method)离散化式(9)得

(10)

式中T——控制器的采样间隔

将式(9)代入式(10)可得

X(t+1|t)=X(t|t)+Tf(X(t|t),U(t|t))

(11)

假设预测时域为Np，控制时域为Nc，则在预测时域内拖挂车的位姿状态为

(12)

若农用拖挂车行驶区域内共有Nz个障碍物点，则可以定义拖车前桥中点、拖车后桥中点和挂车车桥中点在预测时域内的t+i时刻与第j个障碍物点之间的距离为

(13)

式中dqj(t+i|t)——t+i时刻拖车前桥中点与第j个障碍物点之间距离

dhj(t+i|t)——t+i时刻拖车后桥中点与第j个障碍物点之间距离

dgj(t+i|t)——t+i时刻挂车车桥中点与第j个障碍物点之间距离

xzj、yzj——第j个障碍物点的横、纵坐标值

式(13)即为NMPC避障控制器中农用拖挂车与障碍物间距离的预测模型。

NMPC避障控制器另一个关键部分是滚动优化，其优化核心是目标函数。对比文献[12]提出的禁区惩罚函数、文献[13]中提出的反比例惩罚函数和文献[14]中提出的指数惩罚函数可知，禁区惩罚函数具有障碍物边界划分较为清晰等优势，因此本文参照文献[12]提出的禁区惩罚函数，设计如下适用于农用拖挂车避障控制的优化目标函数，若同时满足dqj(t+i|t)>Rq+Rz+Ra，dhj(t+i|t)>Rh+Rz+Ra和dgj(t+i|t)>Rg+Rz+Ra，则

Jj(t+i|t)=0

(14)

否则

Jj(t+i|t)=M

(15)

式中Rq、Rh、Rg——临界半径，其值等于车桥中心到轮胎外沿的距离

Rz——障碍物半径

Ra——安全裕度

M——足够大的正数

此外，为避免求得局部最优解，将式(15)改进为

Jj(t+i|t)=M-dqj(t+i|t)-dhj(t+i|t)-dgj(t+i|t)

(16)

加入文献[13]中的路径跟踪惩罚项Jl，即可得拖挂车避障控制优化目标函数为

(17)

参照文献[13]乘用车的约束条件，在约束条件下求解

(18)

即可获得农用拖挂车避障控制所需的控制变量序列

U*=(U(1),U(2),…,U(Np-1))

(19)

其中第一个元素U(1)即农用拖挂车避障控制器在下一时刻输出的控制变量。

3 仿真验证

本文提出的基于非线性模型预测控制的农用拖挂车避障控制器通过Matlab/Simulink进行仿真验证。仿真系统中包含避障控制器和农用拖挂车的计算机模型。由于计算机模型可以直接给出农用拖挂车的位姿状态信息，所以仿真系统中未包含定位系统和传感系统。仿真中农用拖挂车和NMPC控制器的参数如表1所示。仿真分为对照仿真和复杂工况仿真。

3.1 对照仿真

在这组仿真中，实验组为本文提出的农用拖挂车避障控制器，以下简称拖挂车避障控制器，对照组控制器则为采用乘用车运动学模型作为预测模型的避障控制器，以下简称为拖车避障控制器。在拖车避障控制器中，挂车的位姿状态未考虑。图2显示了实验组农用拖挂车避障控制器的避障控制结果，图3则显示了对照组拖车避障控制器的避障控制结果。图2a和图3a为仿真结果的整体展示，由图可知，拖挂车避障控制器和拖车避障控制器都对障碍物做出了避让控制，且避障结束后，被控的农用拖挂车又回到了给定行驶路径。图2b和图3b则为仿真结果的局部放大，由图可知，在本文提出的拖挂车避障控制器的控制下，农用拖挂车的拖车和挂车都实现了避障；而在拖车避障控制器的控制下，农用拖挂车的拖车避开了障碍物，挂车则与障碍物发生了碰撞。

表1 农用拖挂车及NMPC控制器参数Tab.1 Parameters of agricultural tractor-trailer and parameters of NMPC controller

图2 实验组农用拖挂车避障控制器的避障控制仿真结果Fig.2 Simulation results of obstacle avoidance control based on tractor-trailer obstacle avoidance controller of experimental group

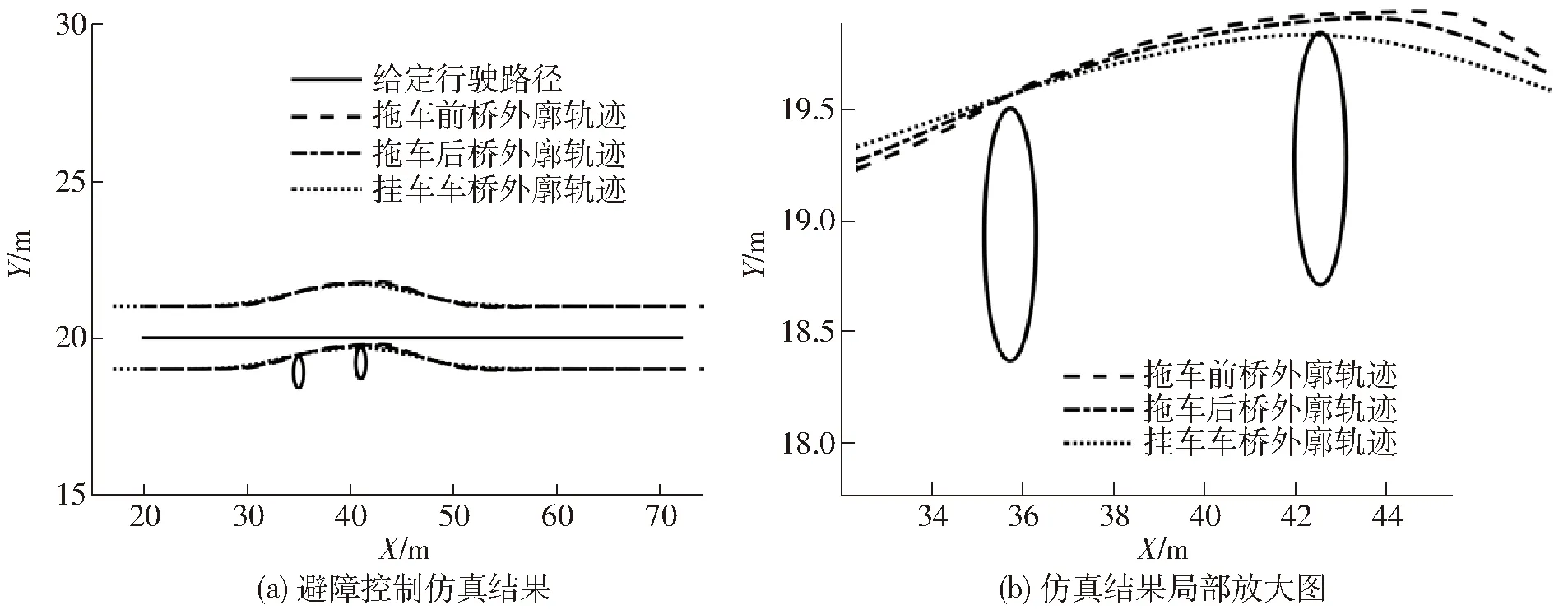
图3 对照组拖车避障控制器的避障控制仿真结果Fig.3 Simulation results of obstacle avoidance control based on tractor obstacle avoidance controller of control group

图4为避障控制过程中的控制变量变化曲线。由图4可知，在仿真过程中，拖挂车避障控制器和拖车避障控制器的控制变量变化都较为平缓，符合农用拖挂车的系统约束。此外，由图4b可知，由于未考虑挂车的位姿状态，拖车控制器在农用拖挂车的拖车驶过障碍物(41,19.2)m后，即控制拖挂车向给定行驶路径靠拢，因此挂车与拖车的内轮差导致挂车与障碍物发生了碰撞。

表2为农用拖挂车的关键位置与障碍物中心的最小距离，在拖挂车避障控制器的控制下，农用拖挂车各桥端点轨迹与各障碍物中心的最小距离为0.550 5 m，减去障碍物半径与安全裕度之和0.550 0 m后大于0 m。在拖车避障控制器的控制下，挂车车桥端点轨迹与障碍物中心(41,19.2)m的最小距离为0.490 5 m，减去障碍物半径0.500 0 m后小于0 m，挂车车桥右端与障碍物发生了碰撞。

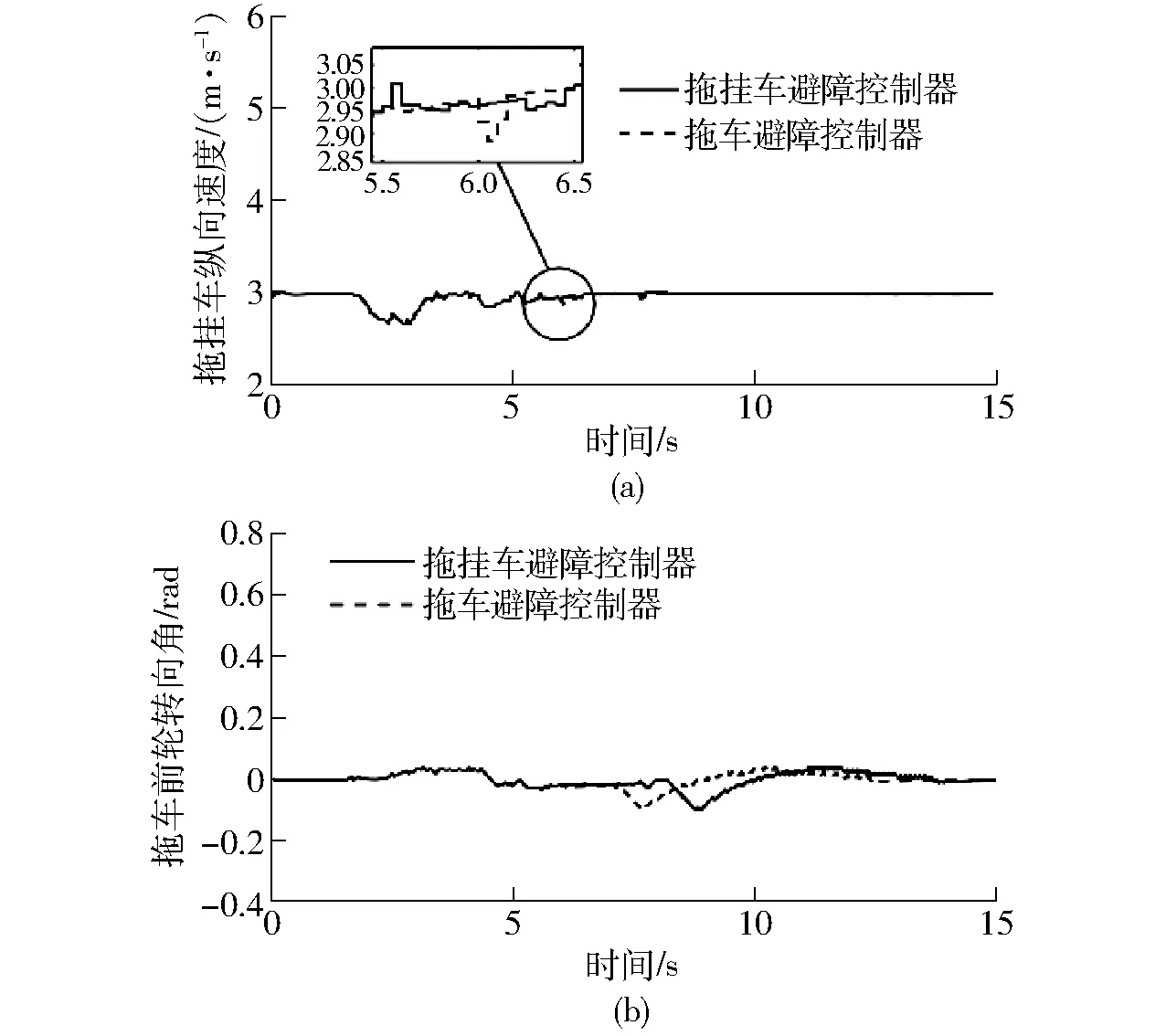
图4 对照仿真的控制变量Fig.4 Control variable of comparison simulation

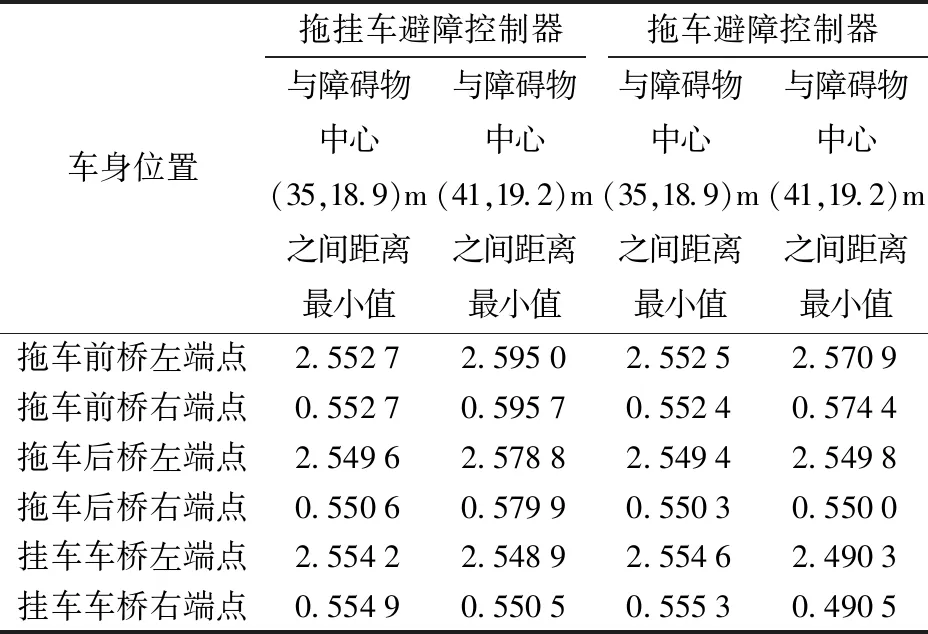
表2 对照仿真中农用拖挂车的关键位置与

3.2 复杂工况仿真

为了进一步测试本文提出的拖挂车避障控制器，在农用拖挂车的给定行驶路径上布置了更多障碍物。由图5可知，在拖挂车避障控制器的控制下，农用拖挂车的拖车和挂车都顺利地实现了避障，并且在完成避障后回到了给定行驶路径。

由图6可知，在避障控制中，控制变量符合农用拖挂车的系统约束条件。

图7为农用拖挂车的拖车后桥与给定形式路径之间的误差曲线，此误差用于表征拖挂车避障控制器在避障后将农用拖挂车与给定行驶路径之间的误差收敛能力。由图7a可知，在完成避障后，农用拖挂车与给定行驶路径的横向误差超调量较小，收敛速度较快，最终收敛为0 m。由图7b可知，航向误差的超调量较小，收敛速度较快，最终收敛为0 rad。

图5 农用拖挂车避障控制仿真结果Fig.5 Simulation results of obstacle avoidance control for agricultural tractor-trailers

图6 复杂工况仿真的控制变量Fig.6 Control variable of simulation of complex condition

图7 拖车后桥中心与给定行驶路径之间的误差Fig.7 Errors between center of rear axle of tractor and given path

表3中，农用拖挂车各桥端点轨迹与障碍物中心的最小距离为0.550 0 m，减去障碍物半径与安全裕度之和0.550 0 m等于0 m。

4 结论

(1)为实现农用拖挂车的避障控制，考虑到农用拖挂车与乘用车不同的车身结构，基于刚体运动学和非完整约束条件推导了农用拖挂车运动学模型，该模型能够同时表达拖车和挂车的位姿状态。

表3 复杂工况仿真中农用拖挂车的关键位置与 障碍物中心的最小距离Tab.3 Minimum distance between key position of agricultural tractor-trailer and center of obstacle in simulation of complex condition m

(2)基于运动学模型推导了农用拖挂车位姿状态预测模型，基于改进的禁区惩罚函数设计了优化目标函数，完成了基于非线性模型预测控制的农用拖挂车避障控制器的设计。仿真结果表明，该控制器能够在较复杂的工况下实现农用拖挂车的避障控制，农用拖挂车各车桥端点轨迹与障碍物中心的最小距离减去障碍物半径与安全裕度之和的结果均大于或等于0 m。

(3)对照仿真结果表明，不考虑挂车位姿状态的拖车避障控制器控制下的农用拖挂车与障碍物发生了碰撞，挂车车桥端点轨迹与障碍物中心的最小距离减去障碍物半径与安全裕度之和的结果小于0 m。通过对比，证明了本文提出的农用拖挂车避障控制器的有效性。

(4)完成避障控制后，本文提出的农用拖挂车避障控制器对路径跟踪性能的影响较小。仿真结果中，农用拖挂车与给定行驶路径之间的横向误差和航向误差均收敛为零，且收敛速度较快。