基于区间两阶段模糊可信性约束模型的灌区水资源配置
岳 琼 郭 萍 王友芝 张成龙 李 鹏
(1.中国农业大学中国农业水问题研究中心, 北京 100083; 2.湖北省漳河工程管理局, 荆门 448156)
0 引言
如何顺应经济社会发展要求、合理高效利用水资源是当前的热点问题[1-2]。随着城镇化规模的扩大,漳河灌区来水量时空分布不均、逐年减少的趋势与用水量大幅增长之间的矛盾日益突出,如何协调灌区各用水户之间的利益冲突、科学优化且合理配置有限的水资源,对提高水资源综合利用效益,保障漳河灌区工农业生产、生态环境以及人类生活的可持续发展具有十分重要的意义[3]。
近些年,针对漳河灌区各用水部门间水资源优化配置问题的研究较少,而且往往忽略或简化了水资源配置系统中的不确定性[4-6]。来水量时空分布不均,规划期供需水量波动,管理者的模糊决策以及市场环境多变等不确定性构成了漳河灌区水资源配置系统的复杂性[7-8]。区间两阶段随机规划(Interval-parameter two-stage stochastic programming, ITSP)模型由于能够处理参数上下限已知而概率分布未知的随机问题而被广泛应用[9-13],模糊可信性约束规划(Fuzzy credibility constrained programming, FCCP)模型由于能够解决带有违规概率的模糊风险问题而备受青睐[14-16]。因此,本文针对漳河灌区水资源系统的复杂性和不确定性,构建各用水部门间水资源优化配置模型,将FCCP模型引入ITSP模型框架,结合随机概率、离散区间和模糊集数学方法,以期实现系统不确定性的衡量以及系统收益与风险的平衡,为灌区管理者提供合理的决策支持。
1 模型建立与求解
1.1 区间两阶段模糊可信性约束规划模型
根据灌区水资源配置系统特征,将区间两阶段随机规划模型与模糊可信性约束规划模型结合,构成区间两阶段模糊可信性约束规划模型,对漳河灌区各用水部门进行优化配水,获得系统最大收益,减小缺水损失,权衡系统收益与违规风险。模型分两个阶段进行最优配置目标及最优配置水量(灌溉面积)的求解,在随机事件发生之前,模型按照预先设置目标进行水量(灌溉面积)分配;当随机事件确定之后,模型对前一阶段的配置目标进行调整,对缺水量(缺灌面积)进行优化配置,尽可能减小系统经济损失。模型考虑效益系数和惩罚系数的模糊不确定性,来水的随机性以及可利用水量的随机模糊特征,同时引入区间参数来解决无法表示为概率分布的不确定性参数,获得决策及收益区间。所建立的优化模型满足以下约束条件:①某一流量水平及置信水平下的配水总量不超过该流量水平及置信水平下的总可利用水量。②某一流量水平下各用水户的配水量介于该流量水平下的最大、最小需水量之间。③某一流量水平下各农业分区的灌溉面积应该介于该流量水平下最大、最小需灌面积之间。④模型的决策变量应始终大于等于0。由此,模型表达式如下:
目标函数为
(1)
约束条件为:
可利用水量约束

(2)
各用水部门需水量约束

(3)
各农业分区需灌面积约束

(4)
非负约束
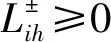
(5)

(6)
式中f±——系统净效益,亿元
i——非农业用水部门,取1~4,分别代表生活用水、工业用水、生态用水、发电用水
j——农业用水分区,取1~3,分别代表荆门市、荆州市、当阳市
h——流量水平,取1~5,分别代表特丰流量水平、偏丰流量水平、中等流量水平、偏枯流量水平、特枯流量水平
ph——h流量水平发生的概率








Cr{·}——事件{·}的可信性测度
λ——可信性置信水平
M±——漳河灌区农业净灌溉用水定额,m3/hm2



Xih,min——i用水部门h流量水平下的最小需水量,m3
Xi,max——i用水部门的最大需水量,m3
Ajh,min——j农业用水分区h流量水平的最小需灌面积,hm2
Aj,max——j农业用水分区最大需灌面积,hm2
其中±表示区间。
1.2 模型求解

(7)
1.2.1上限子模型
目标函数为
(8)
约束条件为:
可用水量约束
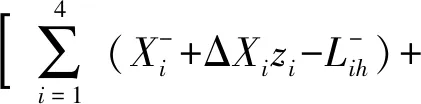
(9)
各用水部门需水量约束
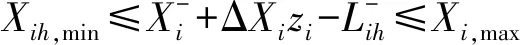
(10)
各农业分区需灌面积约束
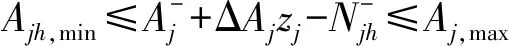
(11)
非负约束
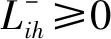
(12)
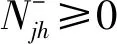
(13)

1.2.2下限子模型
目标函数为
(14)
约束条件为:
可用水量约束
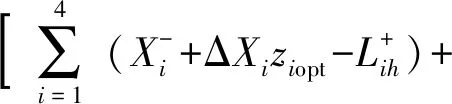
(15)
各用水部门需水量约束
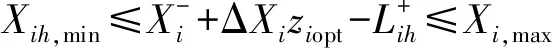
(16)
各农业分区需灌面积约束

(17)
非负约束

(18)
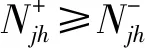
(19)
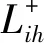
因此在任一α截集下,模型的优化解为
(20)
最优配置目标为
(21)
最优配置结果为
(22)
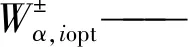

2 实例研究
2.1 研究区域概况
漳河灌区地处长江中下游,位于湖北省中部,属亚热带季风气候,年内温差较大。灌区降水量丰富,多年平均降水量为884.5 mm,但年际丰枯变化较大,且年内分布不均,降水多发生在4—10月。漳河水库是漳河灌区的主要水源,担负着荆门市、荆州市、当阳市部分县区的农田灌溉用水和荆门市的城市工业和生活供水任务,兼有防洪、发电、生态供水等综合效益。随着城市规模不断扩大,灌区社会经济的持续发展对水资源的需求量增长较快,尤其是工业、城镇生活及生态用水需求量大幅增加。在灌区水资源优化配置中,来水及可供水量符合随机分布规律,用水效益所涉及到的相关参数存在一定波动,统计年鉴中的种植面积及灌区水资源利用效率也存在一定的误差,这些不可控的因素都增加了系统的复杂性。本文所建立的模型能够定量表征灌区水资源优化配置系统中的多重不确定性,且有效协调各用水部门的利益冲突,缓解有限水资源条件下的用水供需矛盾,同时帮助管理者深入了解灌区水资源系统的不确定性,权衡系统风险与收益,提出合理的水资源规划与管理方案。
2.2 模型参数确定
以灌区4个非农业用水部门(生活、工业、生态、发电)以及3个农业灌溉分区(荆门市、荆州市、当阳市)为研究对象,进行水量及灌溉面积的优化配置。参考漳河工程管理局提供的各用水部门历年用水统计资料及漳河灌区灌溉台账(2003—2017年)确定模型水量及灌溉面积配置目标,各部门用水效益系数及惩罚系数采用文献[17]中的计算方法得到,计算公式中的参数来源于荆门市统计年鉴及漳河灌区灌溉台账(2003—2017年)。表1、2为不同用水部门的配置目标和相关的经济参数,效益系数及惩罚系数均用三角模糊数[15]表示。如果第一阶段预设目标得到满足,可以获得可观的经济效益,一旦配置目标未得到满足,则会缩减当前规划或从其他途径获取更高成本的水量,从而会有相应地惩罚,导致经济效益的损失。各农业分区的灌溉水利用系数和渠系水利用系数由漳河工程管理局提供(表3)。根据漳河灌区1963—2017年的来水数据,采用经验频率分析方法划分特丰、偏丰、中等、偏枯、特枯5种流量水平。P表示频率,P<12.5%对应特丰流量(h=1),12.5%≤P<37.5%对应偏丰流量(h=2),37.5%≤P<62.5%对应中等流量(h=3),62.5%≤P<87.5%对应偏枯流量(h=4),P≥87.5%对应特枯流量(h=5)。由统计知识可知,当样本数量足够大时,可以用频率近似代替概率,本文水文系列为54年,因此计算历年经验频率作为随机事件发生的概率[17]。对漳河工程管理局提供的历年降雨径流量统计数据进行分析,得到不同流量水平下的可供水量及概率分布(表4)。由于可利用水量兼有随机性和模糊属性,故将其表示为三角模糊数对应其概率分布。 一般来说,有意义的可信性置信水平应该大于0.5[20],故取可信性置信水平为0.80、0.85、0.90、0.95、1.00进行分析。

表1 非农业用水部门的配水目标及相关经济参数Tab.1 Non-agricultural water distribution targets and economic parameters

表2 各农业分区的灌溉面积目标及相关经济参数Tab.2 Agricultural irrigation area distribution targets and economic parameters

表3 各农业分区用水效率系数Tab.3 Water utilization efficiency coefficient of agricultural divisions

表4 可供水量及概率分布Tab.4 Total available water and probability distribution
3 结果与分析
当zi=1时,最优配水目标结果为预设配置目标上限,系统收益较大的同时,也伴随着较大的缺水风险,系统惩罚风险也随之增大;反之,当zi=0时最优配水目标结果为预设配置目标下限,系统收益较小,同时惩罚损失风险也较小。zj服从与zi相同的规律。最优配置目标结果反映了优化模型对系统收益与风险的权衡。表5、6分别为不同可信性置信水平下的优化配水目标结果以及优化灌溉面积目标结果(α=0.8)。图1为当α=0.8、β=0.9时不同流量水平下非农业用水部门配水量及缺水情况,图2为当α=0.8、β=0.9时不同流量水平下各农业分区灌溉面积及缺灌情况。生态及发电用水户的配水目标结果和3个农业分区的灌溉面积目标结果均取其下限(ziopt=0,zjopt=0),结合图1、2的优化配置结果可知,在任一流量水平下,可供水量均不能达到系统配置目标下限,呈现出明显的缺水态势,因此,模型将预设配置目标下限作为最优配置目标以规避缺水风险,减少系统经济损失。相较之下,生活及工业用水户的缺水比例偏小,多数流量下灌区内的可供水量能够满足其用水需求。因此,生活和工业用水户

表5 不同可信性置信水平下的优化配水目标结果Tab.5 Optimal water allocation targets under different credibility levels

表6 不同可信性置信水平下的优化灌溉面积目标结果Tab.6 Optimal irrigation area allocation targets under different credibility levels

图1 不同流量水平下非农业用水部门配水量及 缺水情况(α=0.8、β=0.9)Fig.1 Non-agricultural water allocation and water shortage under different inflow levels(α=0.8,β=0.9)
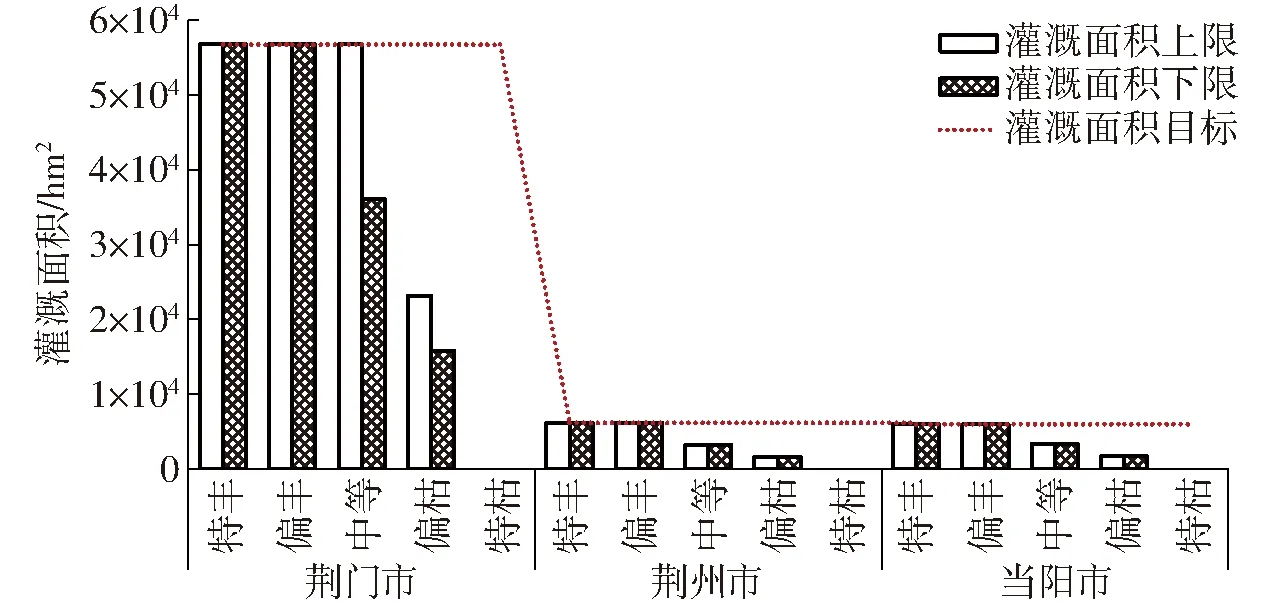
图2 不同流量水平下各农业分区灌溉面积及 缺灌情况(α=0.8、β=0.9)Fig.2 Agricultural irrigation area allocation and area shortage under different inflow levels(α=0.8,β=0.9)
在不同置信水平下的ziopt值略高于其他用水部门,以期获得更高的经济效益。总体而言,优化模型更侧重于规避高违规风险,选择适当的优化配置目标,不盲目追求高系统收益。
考虑不同可信性置信水平下的优化配水量及灌溉面积,不同流量水平下的配水结果是不同的,低流量下的可供水量较小,因此分配给各个用水户的水量较少,相反的,高流量水平下的可供水量较充足,各部门的缺水量较小。以α=0.8、β=0.9为例,4个非农业用水户的优化配水量(图1)随流量水平的增加而增加,其中,发电用户的配水量最大,这与优化配置目标相关。当可供水量无法满足第一阶段的预设配置目标,会造成部分用水户缺水。在特丰流量水平下,除发电用水户外所有用水户均不存在缺水现象。随着可供水量的不断减少,各用水户先后出现不同程度的缺水,且缺水比例呈显著增长趋势。生活用水在特枯流量水平下存在较低程度的短缺,工业用水在偏枯及特枯流量下不能够被满足,生态用水在中等、偏枯及特枯水平下存在不同程度的短缺,而发电用水在各流量水平下均不能够得到满足。以上结果表明,优化模型对各用水部门进行配水的优先级为生活用水最高,工业用水次之,生态部门更次,发电用户最低。在实际调度过程中,当各部门用水需求有矛盾时,漳河工程管理局秉持“城镇用水优先”的原则,通过限制发电用水,优先满足其他部门用水需求,该优化结果与实际情况高度吻合,可行性强。然而,若发电用水严重短缺,一方面将对灌区社会经济效益造成损失;另一方面,由于发电尾水作为生态用水向下游排放,其水量也会对生态环境保护造成一定消极影响。因此,在有必要的情况下,对漳河水库进行扩容,或增强中小型水库和塘堰的蓄水能力,也是一种策略。
由于不同流量水平下的可供水量不同,灌溉面积也不同(图2)。以α=0.8、β=0.9为例,高流量水平下的灌溉面积较大,低流量水平下的灌溉面积较小。当可供水量无法满足农业用水户的灌溉面积目标,会导致部分农业用水户的种植面积缺灌。在高流量水平下,可供水量在各农业分区的缺灌面积比例较小。各分区的缺灌面积比例随着入流量的减少而增加。在偏枯流量水平下,3个分区的缺灌面积比例最高可达75%,在特枯流量水平下,3个分区的所有种植面积将得不到灌溉。其中,荆州市及当阳市的缺灌情况尤为严重,这一方面是由于满足非农业用水户的用水需求,而相应减少农业用户供水量,另一方面是由于荆州市与当阳市与漳河水库在地理位置上有一定距离,在明渠输水过程中将产生一定的水量损失,故优化模型优先对距离漳河水库较近的荆门市配水。因此建议采取一定的工程措施,提高灌区内水资源利用效率,减少不必要的渗漏损失。另外,过低的灌溉水量将影响作物正常生长,限制当地农业的发展,因此,建议可以从其他途径例如外调水等获取一定的灌溉水量。同时,灌溉定额的制定很大程度上决定了农业灌溉用水量,从而影响灌溉面积优化结果。漳河灌区内以雨养农业为主,作物实际灌溉水量与当年实际降雨径流直接相关,因此,建议当地管理者从作物需水的角度出发,针对不同的水文年型,制定不同的灌溉定额,在保障作物实际需求的同时提高水资源的利用效率。
考虑不同的流量水平,不同的可信性置信水平下的配水结果是不同的。以发电用水及荆门市农业灌溉为例,图3、4分别为其不同流量水平及可信性置信水平下水量以及灌溉面积配置结果。结果表明,特丰年及偏丰年时,随着可信性置信水平的降低,分配给发电用水户的水量不断增加,伴随着缺水违规风险不断升高,系统可靠性不断降低。其他用水户的水量优化配置结果也具有相同的规律。同样的,随着置信水平的降低,模型分配给农业分区的灌溉面积不断增加,随之而来的系统风险也不断升高。优化结果以区间形式表示,为决策者提供配置范围,从而决策者可根据实际情况结合自身偏好制定最终配置方案。乐观型决策者愿意承担一定的违规风险,选择配置区间上限值,以获得较高的系统收益;保守型决策者会倾向于选择区间下限值以避免较高的缺水风险,同时,获得的系统收益相对较低。

图3 不同流量水平及可信性置信水平下发电用水 部门水量配置结果Fig.3 Optimal water allocation schemes for power sector under different inflow and credibility levels

图4 不同流量水平及可信性置信水平下荆门市 灌溉面积配置结果Fig.4 Optimal irrigation area allocation schemes for Jingmen under different inflow and credibility levels
图5为不同可信性置信水平及隶属度水平下的系统经济效益。系统收益的上限值随α水平的增加而逐渐减小,相反的,系统收益的下限值随α水平的增加而增加,这与本文选用的三角模糊隶属度函数的形状直接相关。对于三角模糊隶属度函数,α水平越大代表模糊事件发生的概率越小,系统的模糊程度越低,反之亦然。因此,随着α水平不断增加,系统收益的取值范围越来越小,即取值越来越接近确定型模型结果。当α=1时,系统收益区间将趋于0,模型中相关经济参数的模糊特性将不存在。相反的,α=0是另一种极端情况,代表模型参数的模糊特征最强,区间范围最大。另外,在同一α水平下,系统的效益在不同的违规概率下存在差异。以α=0.6为例,系统效益随着违规概率的增加而增加,这是由于随着系统违规程度增加,模型更加放松了可利用水量约束,可利用水总量增加,分配给各用水户的水量随之增加,系统经济收益也有所提高。因此,灌区管理者可以结合个人偏好权衡系统收益和系统可靠性,制定相应的水资源优化配置方案。

图5 不同可信性置信水平及隶属度水平下的经济效益Fig.5 System benefits under different credibility and membership levels
4 结论
(1)针对灌区配水系统中存在的多重不确定性,采用耦合区间、模糊、两阶段随机规划以及模糊可信性约束规划等理论方法,构建不确定条件下的区间两阶段模糊可信性约束规划模型。该模型能切实反映灌区水资源管理的不确定性,同时将系统收益与违规风险紧密联系在一起,为管理者提供合理的决策支持。
(2)给出模型的表达形式及求解方法,将不确定性模型转换为确定性的上下限子模型进行求解。将所构建的模型应用于湖北省漳河灌区各部门配水管理中,得出多种组合情景下的系统经济效益,生活、工业、生态、发电4个非农业用水户优化配水量,以及荆门市、荆州市、当阳市3个农业分区的优化灌溉面积。结果表明,模型更侧重于规避风险,降低系统违规损失,当置信水平为0.8时,系统总收益高达[10.26亿元,13.25亿元]。模型优化结果有助于管理者更深入了解系统的不确定性,以便更好地平衡系统收益与风险。
(3)总体来看,漳河灌区水资源短缺。在低流量水平下,各用水户(分区)有很大的缺水比例(缺灌面积比例)。结合灌区实际情况,从灌区可持续发展角度出发,一方面建议限制发电用水以满足农业灌溉及其他部门用水需求,另一方面建议采取更多工程及农艺节水措施,充分挖掘灌区节水潜力。

