基于似然比检验的橡胶密封件加速试验机理一致性判别方法*
鲁 相,汪亚顺,陈 循,谭源源
(1. 国防科技大学 智能科学学院, 湖南 长沙 410073; 2. 中国空气动力研究与发展中心 设备设计及测试技术研究所, 四川 绵阳 621000)
随着产品质量水平的不断提高,近代研制出的产品普遍具有高可靠、长寿命的特点,例如发光二极管及橡胶密封件等元器件中位寿命可以超过10年[1]。对于这类高可靠性产品,现代工业广泛利用加速退化试验预测其使用寿命和贮存寿命。在加速退化试验中,将产品置于加速应力水平下并记录产品样本的性能退化数据,利用加速模型建立应力与退化速率之间的关系。当各试验应力水平下的失效机理相同时,就可以将加速应力下的试验结果外推,进而估计在正常应力状况下的产品寿命。各试验应力水平下失效机理具有一致性是加速退化试验结论具备有效性的首要前提,因此需要研究加速退化试验机理一致性判别方法。
利用试验数据统计分析方法或物理分析测试手段,判断失效机理在试验各加速应力水平下是否发生变化,这个过程被定义为失效机理的一致性判别。目前失效机理一致性判别方法可分为3类:概率图检验法[2-4]、基于模型参数一致性检验法[5-9]、基于灰色预测模型检验法[10-11]。这些一致性判别方法各有优劣,但存在共同的缺点:通常只对寿命服从某一特定分布的产品有效,应用场合受限,因而难以推广到其他统计分布,并且这些方法对判别结果的误判风险没有开展定量分析。因此,提出基于似然比检验的失效机理一致性判别方法,该方法适用于多个统计分布,可以定量分析误判风险,并且模型参数估计精度较高。
1 机理一致性判别的数学模型及参数估计
1.1 两类加速模型
通常利用混合效应模型[12-13]对高可靠产品退化建模,并认为性能退化量初始值B及退化轨迹形状参数α是固定不变的,不同个体间的退化速率存在差异。产品的退化速率Kij在各应力水平Si下一般服从对数正态分布LN(μi,σ2),其中σ为对数标准差,μi为对数均值(与应力水平有关)。选择如式(1)所示的混合效应模型。
(1)

在混合效应模型下,当失效机理不变时,提高载荷或温度的试验产品统一加速模型为:
μi=a+b·φ(Si)
(2)
式中,φ(Si)为转换应力水平,温度为加速应力时φ(Si)=1/Si,载荷为加速应力时φ(Si)=lnSi。
当加速应力范围较大导致失效机理变化时,式(2)中的参数a和b不再为常数,式(2)在较高应力水平下无效。比式(2)更适用的模型可以表述为:
μi=ai+bi·φ(Si)
(3)
可得到如下原假设H0:μi=a+b·φ(Si)和备择假设H1:μi=ai+bi·φ(Si)。
从上述定义可以看出,在原假设中假定退化速率-应力关系为对数线性,将原假设对应模型称为对数线性加速模型。相比之下,在备择假设中模型参数与应力水平有关,将备择假设对应模型称为非对数线性加速模型。式(2)与式(3)的表达式表明原假设对应模型是备择假设对应模型的一种特例。在对数线性加速模型中参数a和b被限定为常数,导致其独立参数少于非对数线性加速模型。如果两种假设模型中一种模型是另一模型的特例,则可用似然比检验比较两种模型的拟合优度[14-15],因此似然比检验可用于检验上述原假设。
1.2 似然比检验的基本准则
假定有来自于分布T的随机样本t1,t2,…,tn,令θ表示该分布未知参数向量,则该样本的似然函数为:
(4)
令L0(θ)为对数线性加速模型参数的似然函数,L1(θ)为非对数线性加速模型参数的似然函数。对数线性加速模型参数的极大似然估计(Maximum Likelihood Estimation, MLE)为:
(5)
非对数线性加速模型参数的极大似然估计为:
(6)
似然比统计量可表示为:
(7)
由于包含更多独立参数,通常非对数线性模型对样本观测值的拟合效果比对数线性模型好,但两类模型也可能都有较好的拟合效果。非对数线性模型参数的似然函数值不小于对数线性模型的似然函数值,似然比统计量满足:
(8)
如果对数线性模型与非对数线性模型一样适用,则似然比较大,反之较小。当似然比统计量数值过小时似然比检验法会拒绝原假设(对数线性加速模型),似然比检验法的临界域或拒绝域为:
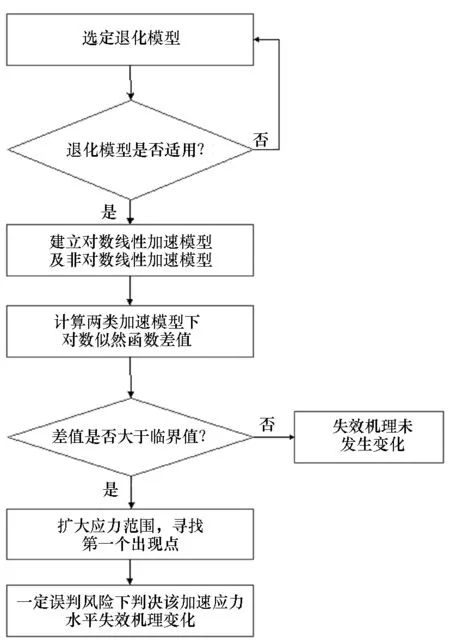
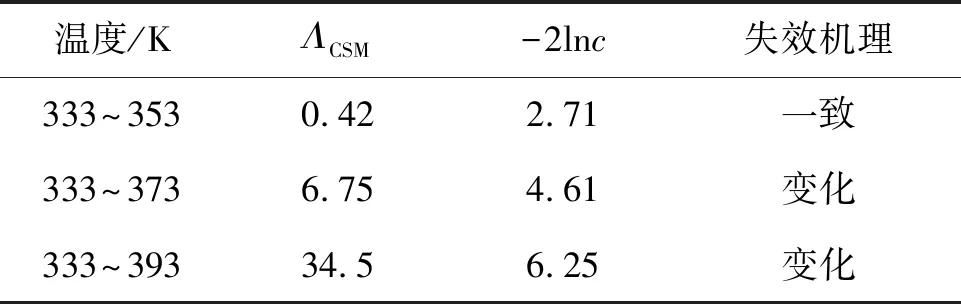
W={λ≤c} 0 (9) 式中,临界值c与参数λ、β有关。β是似然比检验中规定的显著性水平,β表示将失效机理相同误判为失效机理变化的风险大小。 根据上述分析,首次应用似然比检验法辨识加速退化试验中加速模型的变化,并计算两种假设模型下对数似然函数的极大值。设恒定应力加速退化试验(Constant Stress Accelerated Degradation Testing, CSADT)采用q个应力水平,在每个加速应力水平Si(i=1,2,…,q)下测试ni个试验样本的性能退化量,测试mi次,测试的时间节点为tik(k=1,2,…,mi),在每个应力水平下的试验截止时间为ti,测得退化量数据为yijk(j=1,2,…,ni)。建模时取样本的性能退化量对数值lnyijk统计分析,混合效应模型下其条件累积分布及条件概率密度函数可以表示为: (10) (11) 其中,Φ(·)和φ(·)表示标准正态分布的累积分布函数及概率密度函数。由式(10)及式(11)可得恒定应力加速退化试验数据的似然函数为: (12) 式中,f(Kij)代表退化速率Kij的概率密度函数。 (13) 假定采用温度作为加速应力,在对数线性加速模型中ai=a,bi=b,取向量δ=(lnB,α,a,b),Kij=exp(a+b/Si+cij),yijk=(yij1,…,yijmi)T,tik=(ti1,…,timi)T,协方差矩阵D=σ2,cij服从正态分布N(0,σ2)。采用近似极大似然估计法求解模型参数。 步骤1:在固定协方差矩阵的情况下,用非线性最小二乘法获得加速模型参数a、b、cij和形状参数α及退化量初始值B的估计值,估计值是使式(14)最小化的解。 (14) 步骤2:首先将模型函数在第一步获得的各参数估计值处作Taylor展开,根据模型函数表达式,有 其中, *代表哈达马积。 然后利用第一步获得的估计值求取协方差矩阵D及其他参数的极大似然函数表达式,取 可得对数线性加速模型的对数似然函数为: (15) 设定好数值迭代算法的初始解,利用Newton-Raphson算法[16-19]求解未知参数估计值,按式(15)计算对数似然函数的极大值。 在非对数线性加速模型中,取向量κ=(lnB,α,μ1,…,μq),Kij=exp(μi+cij),yijk=(yij1,…,yijmi)T,tik=(ti1,…,timi)T,协方差矩阵D=[σ2]。 按以下步骤进行参数估计。 步骤1:在固定协方差矩阵的情况下,用非线性最小二乘法获得加速模型参数μi、cij和形状参数α及退化量初始值B的估计值,估计值是使式(16)最小化的解。 (16) 步骤2:首先将模型函数在第一步获得的各参数估计值处作Taylor展开,根据模型函数表达式,有 同样求取协方差矩阵D及其他参数的极大似然函数表达式,取 可得非对数线性加速模型的对数似然函数为: (17) 利用Newton-Raphson算法类似得到对数似然函数的极大值。 算出两种假设下似然函数极大值后,需要确定似然比统计量的分布,以构建判别准则。多数情况下难以确定似然比统计量λ的精确抽样分布,但可以确定大样本场合下对数似然比统计量的渐进分布,令 (18) 根据Wilks提出的广义似然比统计量的极限分布定理[20],在原假设成立的情况下,统计量Λ渐进服从自由度为v的卡方分布χ2(v)。自由度v等于在假设H0和H1下的独立参数数目之差,有v=q-2。由式(9)可知,当λ≤c时原假设H0被拒绝,因此当Λ≥-2lnc时对数线性加速模型无效。利用显著性水平β及统计量Λ的分布,可以得出 (19) 式中,等式右端表示卡方分布χ2(q-2)的1-β分位数。 利用式(15)和式(17)计算恒定应力加速退化试验中两类模型的极大对数似然函数的差值,得到: ΛCSM=-2[lnL0(δ,D,σε)-lnL1(κ,D,σε)] (20) 失效机理一致性的判别准则是: 1)如果0<ΛCSM<-2lnc,失效机理在所有应力水平下相同; 2)如果ΛCSM≥-2lnc,失效机理在某一高应力水平下变化。 根据上述分析,基于似然比检验的失效机理一致性判别方法流程如图1所示。 在发光二极管(Light Emitting Diode, LED)加速试验中,最高温度下激活能可能发生变化。本例中设定退化失效机理发生变化,在378 K激活能从16.1 kJ/mol转变为32.2 kJ/mol。 图1 失效机理一致性判别方法流程Fig.1 Flow chart of identification method of failure mechanism consistency 仿真试验温度应力水平为298 K、338 K、378 K,试验样本量为6,测量间隔为336 h,每个水平下测量次数为11。设定退化模型参数分别为a1=-0.546 6,b1=-1933.25(298~338 K),a2=5.173 1,b2=-3866.49(338~378 K),B=1.051 6,α=0.65,σ=0.185,σε=0.014。利用式(1)生成仿真退化轨迹。 利用近似极大似然估计法分析仿真数据,得出对数线性模型中未知参数的极大似然估计,将极大似然估计值与未知参数真值进行比较,结果如表1所示。 表1结果表明,采用指定的加速模型进行建模及统计分析时,加速模型参数估计值a、b与真值的偏差较大,估计值近似于两真值的均值,导致在298 K以下的预测寿命偏大。 表1 对数线性模型参数估计值 非对数线性模型中未知参数极大似然估计值与真值的比较如表2所示,可以看出,模型各参数的估计值与真值相差较小,非对数线性模型拟合效果明显优于对数线性模型。 进一步可以算得温度水平在298~378 K下检验统计量为: ΛCSM=-2lnλ=-2(lnL0-lnL1) =-2×(510.254 7-518.963 2)=17.417 (21) 在298~378 K温度范围内的试验应力水平数为3,给定显著性水平β=5%,临界值满足-2lnc=3.84<ΛCSM。因此在298~378 K范围内失效机理发生变化,这一判别结果与失效机理发生变化的原始设定相符,验证了方法的正确性。 表2 非对数线性模型参数估计值 丁腈橡胶密封件是典型的高可靠性产品,但易于发生热氧老化。受热氧老化的影响,丁腈橡胶密封件在贮存或使用期密封性能会不断退化。随着密封性能的退化,橡胶密封性能的高弹性复原力不断减小,压缩永久变形不断增大。因此可以通过观测压缩永久变形cs的变化来监测退化趋势,当压缩永久变形上升到某一临界值时,认为橡胶密封件密封失效。试验采用安装于系统中的橡胶密封件的压缩率,样本可以代表在空气介质存储下系统内受压丁腈橡胶密封件的退化。试验总样本量为20,选择在5个温度应力水平(333 K、343 K、353 K、373 K、393 K)下进行加速退化试验,每个应力水平下样本量为4。密封件在333 K及393 K应力水平下测得的压缩永久变形量如图2所示,其他应力水平下曲线形状类似,不再给出。根据图1所示流程对数据进行失效机理一致性判别。建立退化模型,将测得的压缩永久变形cs(无量纲)转换为性能退化数据y,转换关系式为y=1-cs,采用混合效应模型(1)对试样退化规律进行描述。 (a) 333 K丁腈密封圈加速退化试验数据 (a) CSADT data of nitrile seal rings at 333 K (b) 393 K丁腈密封圈加速退化试验数据 (b) CSADT data of nitrile seal rings at 393 K图2 丁腈密封圈恒定应力加速退化试验数据Fig.2 CSADT data of nitrile seal rings 利用近似极大似然估计方法,令ni=4(i=1,2,3),可求解333~353 K、333~373 K及333~393 K下模型的未知参数,设定显著性水平β=10%,进一步算得密封圈试样在三个不同温度范围的假设检验结果,如表3所示。 表3 密封圈失效机理一致性判别 根据失效机理一致性判别方法,结合表3计算结果可知,试验所用丁腈橡胶密封圈在373 K以上时温度失效机理发生变化。Wise等[21]、Le等[22]对类似产品开展失效物理分析,得到368 K温度以上丁腈橡胶失效机理变化的结果,与本文所得结论基本一致,验证了本文方法的有效性。 高可靠性产品在进行加速退化试验时,失效机理在高应力水平下可能发生变化,导致错误的寿命预测结果。基于似然比检验的加速退化试验机理一致性判别方法,适用范围广,能够定量分析误判风险,并给出机理一致性判别结论,得到准确的寿命预测结果。建立非线性加速模型与高可靠长寿命产品失效机理变化间的联系,并将似然比检验应用于加速退化试验中对加速模型的辨识,建立了有效的失效机理一致性判别准则及方法。 通过仿真案例及应用实例,进一步验证了所提方法的有效性。多应力加速退化试验下产品失效机理的一致性判别较为复杂,相关方法还需要进一步研究。1.3 数学模型及参数估计
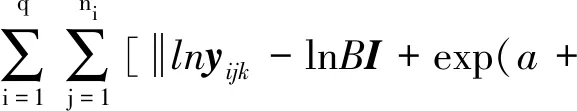

2 失效机理一致性判别准则及方法流程
3 仿真算例


4 应用实例


5 结论

