一类捕食者带有传染病的捕食模型的定性分析

王雅萍

(江苏商贸职业学院， 江苏 南通 226001)

一、模型的背景及问题的提出

传染病的出现可能会极大的改变生态系统的动力学性质，因此，将种群动力学和流行病动力学相结合研究传染病是非常必要的[1-6]。本文将研究一种捕食者带有传染病的生态——流行病模型[7]对应的加入交错扩散项反应扩散问题[8-9]：

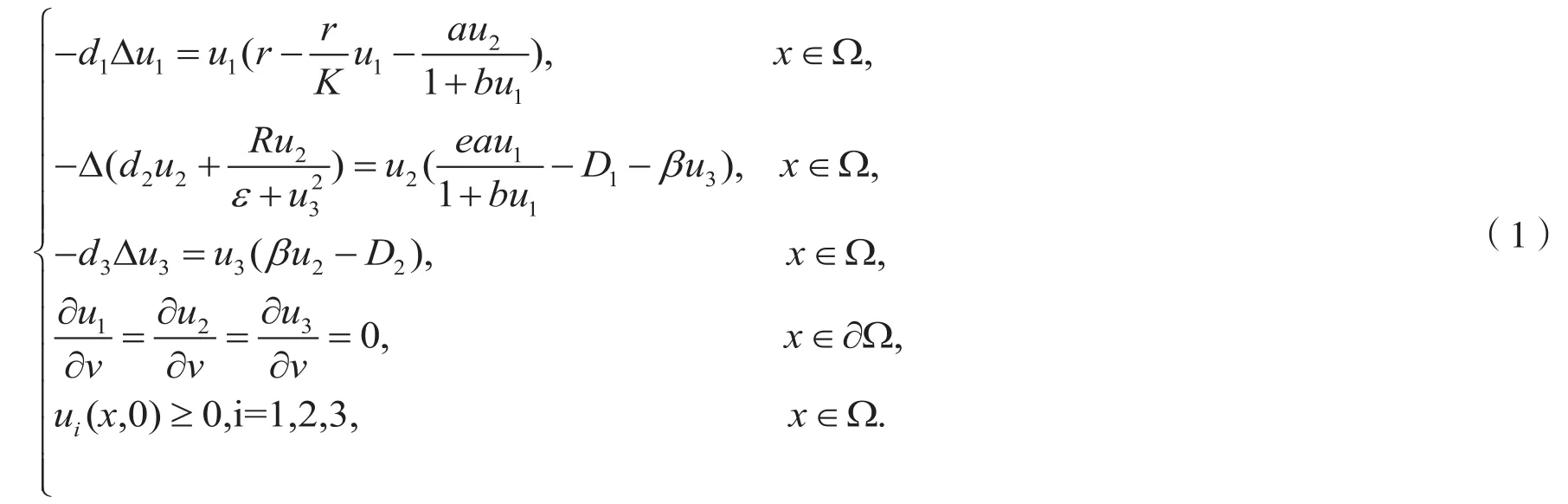
其中：u1表示食饵的密度，u2表示易感类捕食者的密度，u3表示染病类捕食者的密度;r表示食饵的内禀增长率，K表示食饵的最大容纳量，a是捕食系数，e是转化系数，β为接触率;R为交错扩散系数;D1表示易感类捕食者的死亡率，D2表示染病类捕食者的死亡率，由于要考虑因病死亡，所以D1＜D2。v表示Ω上的单位外法向量，以上所有系数都是正常数。初值u1（x, 0）, u2（x,0）, u3（x, 0）,都是连续函数。Ω是中的一个具有光滑边界的有界区域。捕食者与被捕食者在区域内的分布密度不均匀。

二、正常数平衡解的局部分析

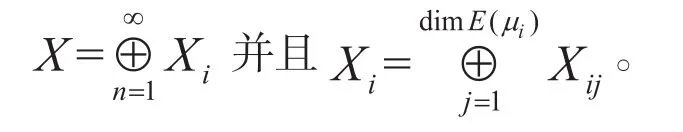
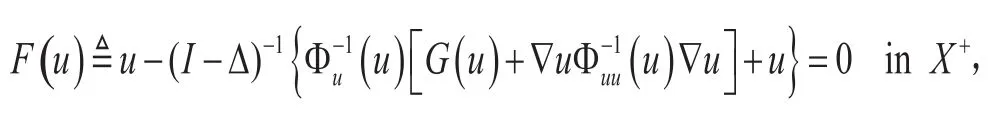
这里(I-Δ)-1为I-Δ 在x上的逆算子。由于F(·)是单位算子的一个紧摄动，所以对任意的B=B(C)，只要在B上F(u)≠0，Leray-Schauder度 deg(F(·),0,B)就有定义。

进一步，我们有

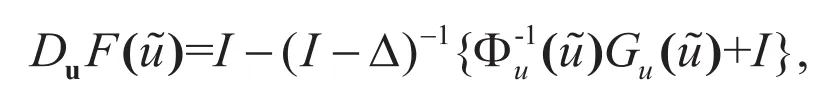
对于每个整数i≥1与每个整数，为的不变子空间，且λ为在上的一个特征值当且仅当它是以下矩阵的一个特征值

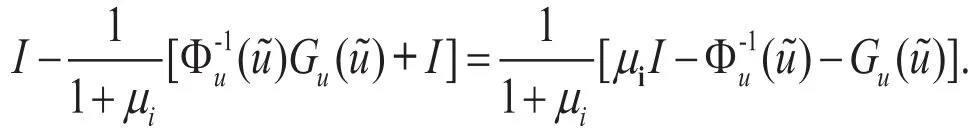
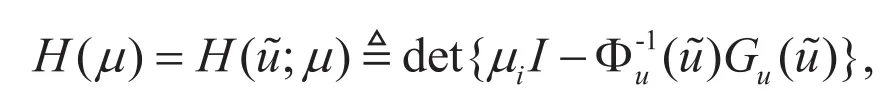
因此，我们有如下结论：

命题1假设对所有的i≥1，矩阵是非奇异的。那么

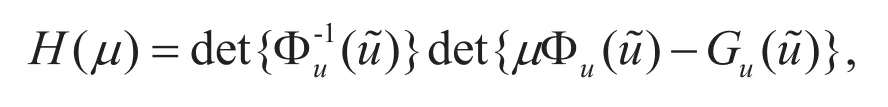
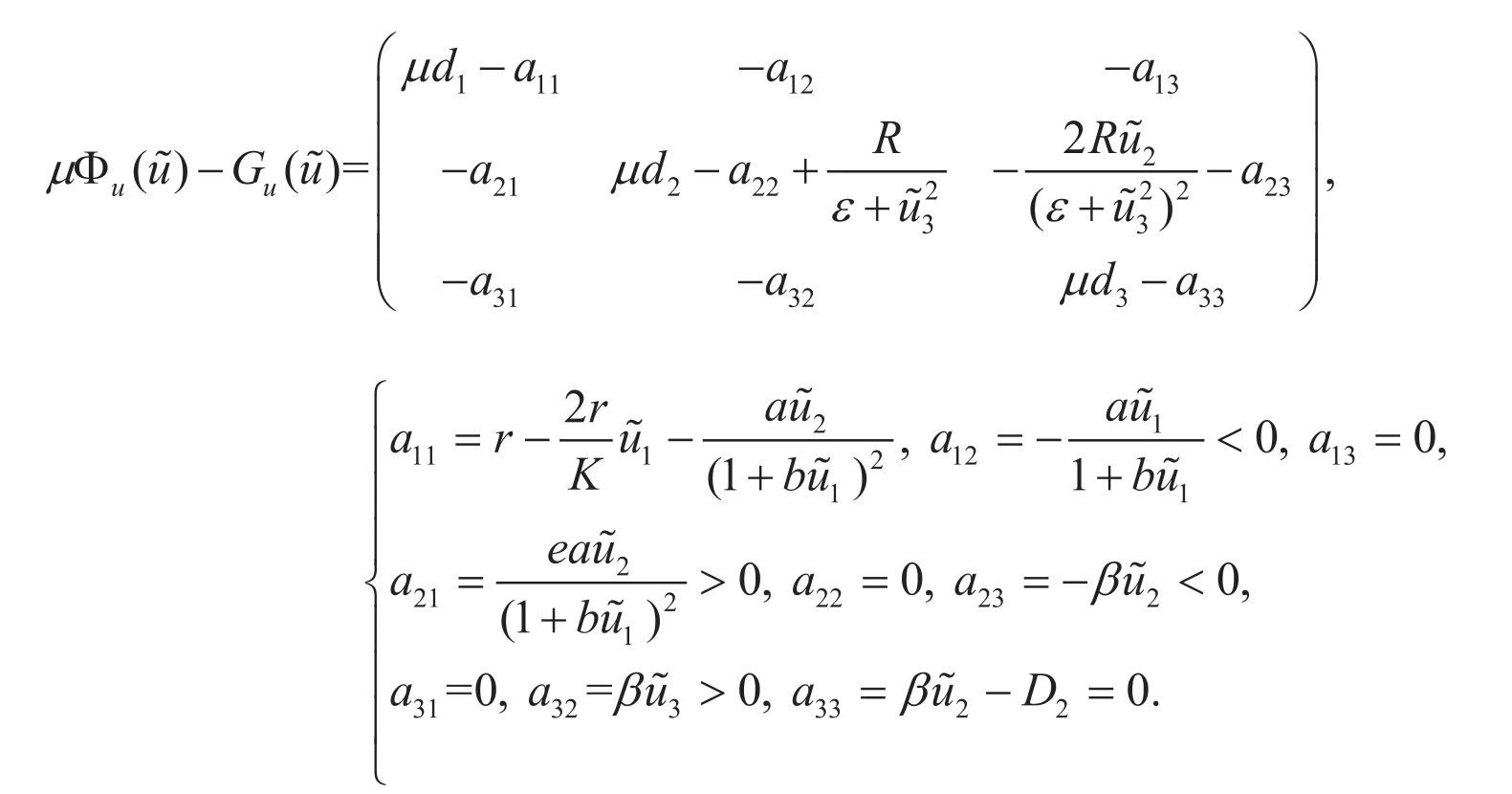
我们有

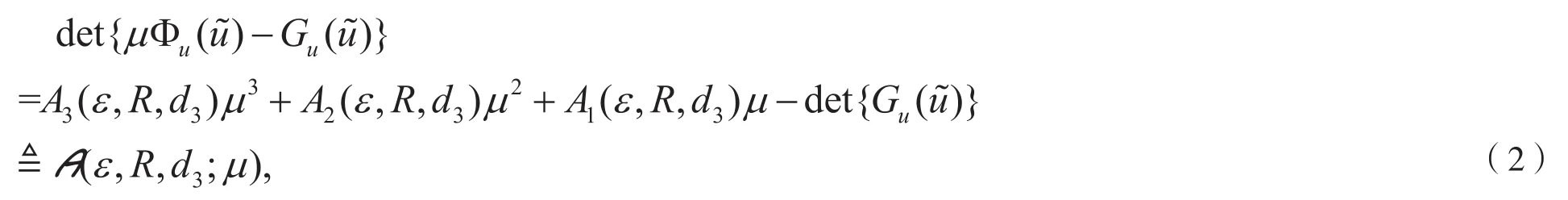
其中

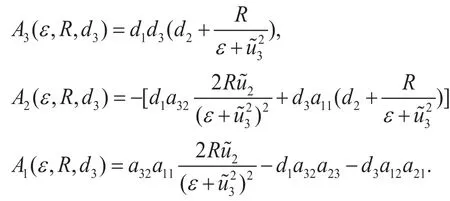
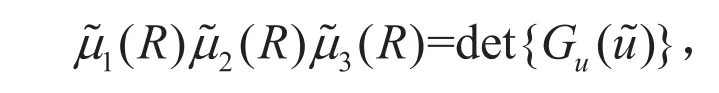
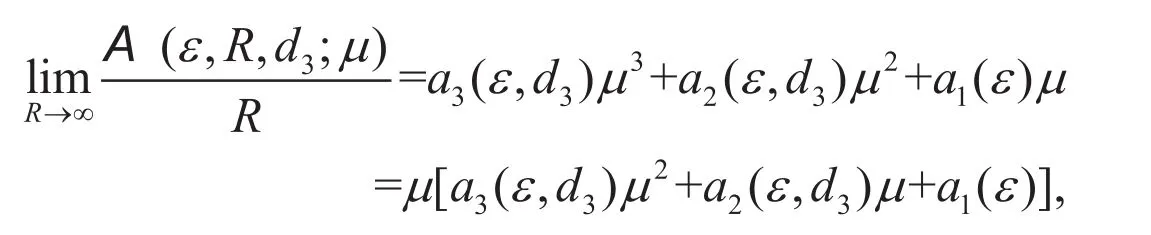
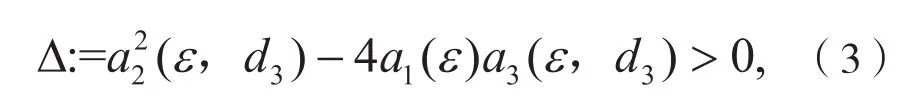
利用连续性可知，当R很大时，为负实数。进一步的，由于，所以都为正实数，并且

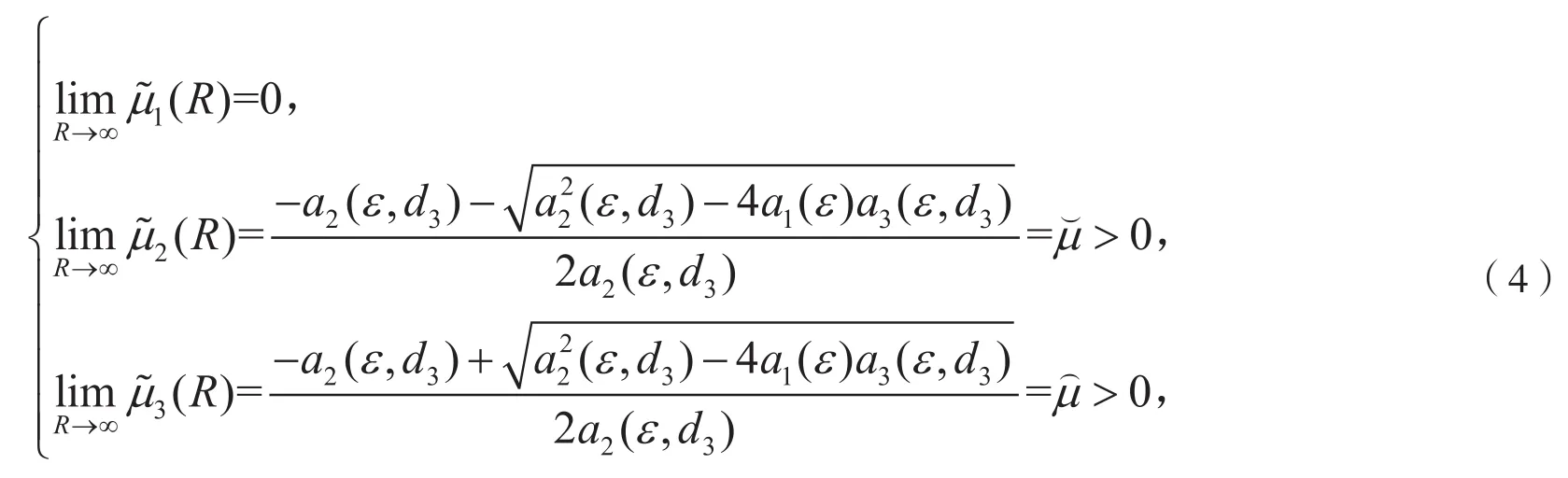
由此，我们得到以下命题：

命 题2假 设且 条件(3)成立，则存在正常数使得当时，代数方程的三个根都是实数，并且满足式(4)。此外，对所有的，

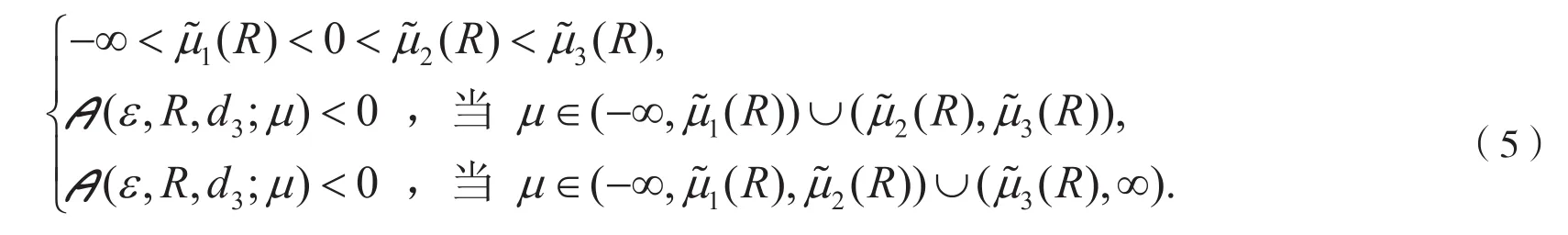
同上，考虑极限

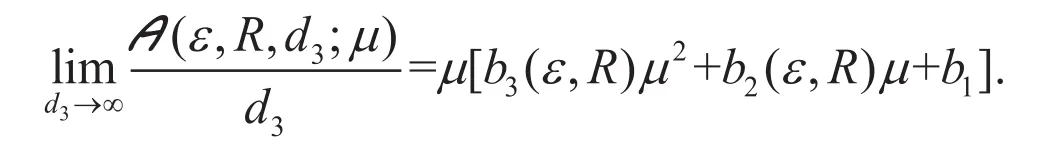
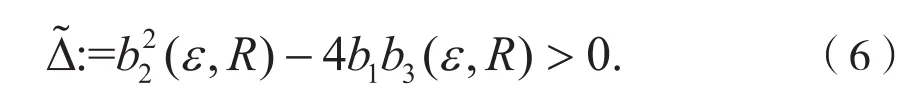
时，可以得到与命题2类似的结果。

命题3假设条件(6)成立，且交错扩散系数R很大，则存在正常数D，使得当时，代数方程的三个根都是实数，并且满足：

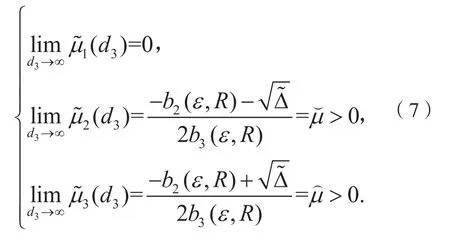
三、正平衡解的全局存在性

定理1固定参数和，使得并且条件(3)成立。取由极限(4)确定，如果对于某，有，并且和

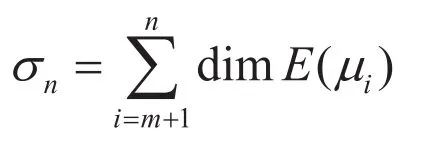
证明：由极限(4)与命题2知，存在正常数，使得当时，式(5)成立，并且

我们将利用拓扑度的同伦不变性采用反证法来证明，对于任意的，问题(1)至少有一个非常数正解。

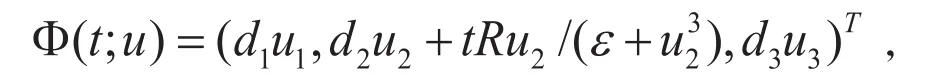
考虑边值问题

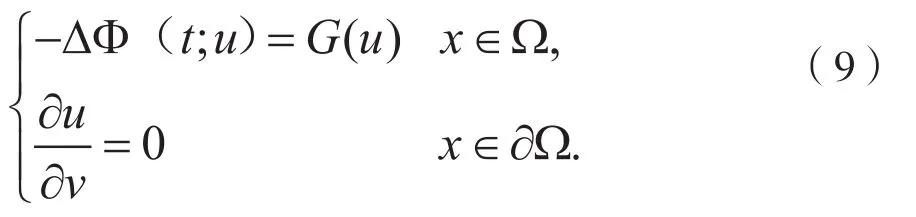
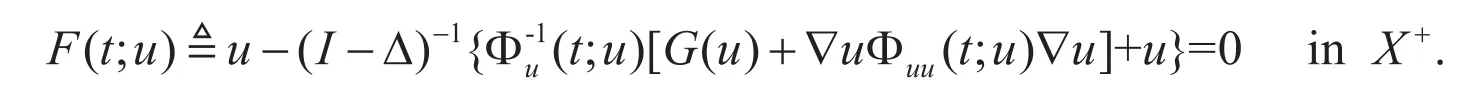
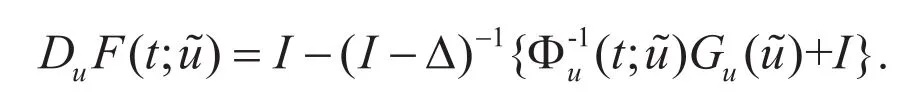
特别的，

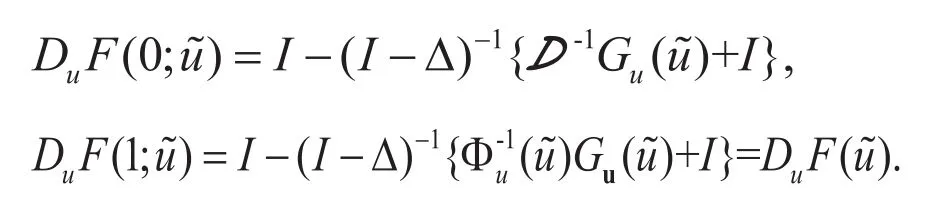
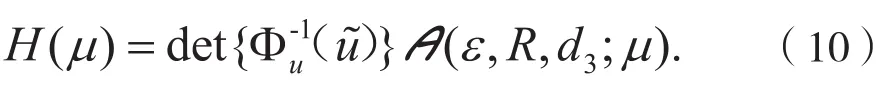
由式(5)和式(8)，从关系式(9)可推出

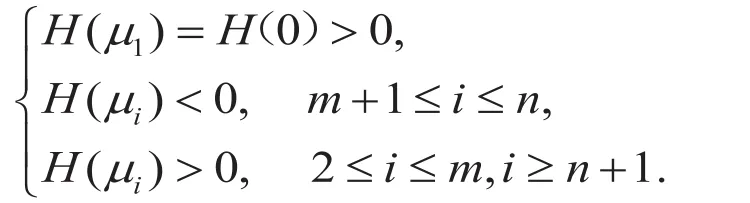
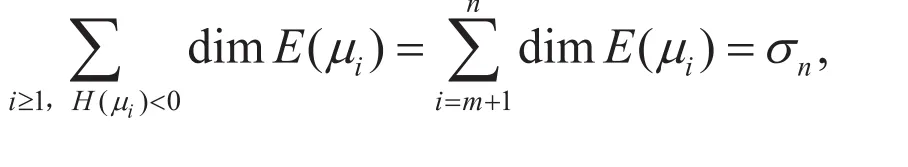
是奇数。由命题1，我们得到

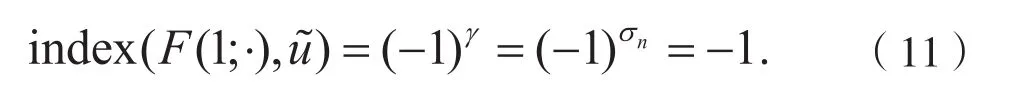
类似的，有

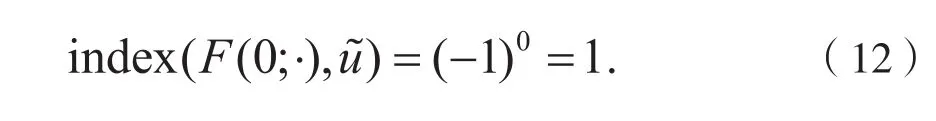
根据上下界估计，存在正常数C，使得对所有的，问题(9)的正解满足。

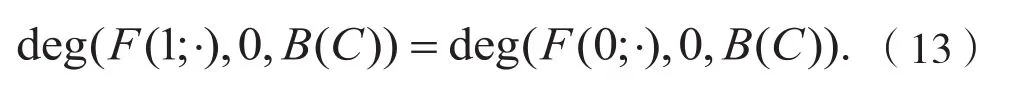
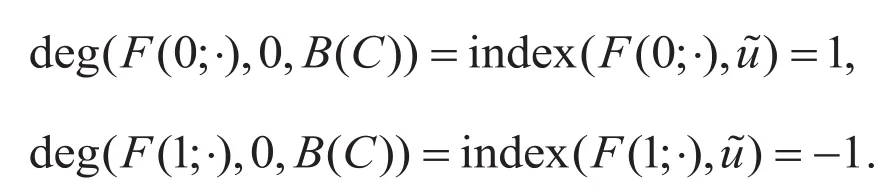
这与式(13)矛盾。证毕。

类似的有如下结论：

定理2固定参数和，使得并且条件(6)成立。取由极限(7)确定，如果对于某，有并且和