梁拱组合体系桥整体节点有限元分析方法对比研究

杨鹰，盛兴旺，郑纬奇，戴劲, 2



梁拱组合体系桥整体节点有限元分析方法对比研究

杨鹰1，盛兴旺1，郑纬奇1，戴劲1, 2

(1. 中南大学 土木工程学院，湖南 长沙 410075； 2. 湖南省水利水电勘测设计研究总院，湖南 长沙 410000)

采用基于力边界条件的节段模型分析方法、基于位移边界条件的节段模型分析方法以及多尺度模型分析方法，对大跨度梁拱组合体系桥梁中的某个整体节点进行有限元仿真分析，并结合现场试验，分析该整体节点的力学性能，对比研究梁拱组合体系桥梁复杂整体节点结构有限元分析方法。研究结果表明：各测点的理论值与实测值差异大多在20%以内，较为吻合；由于整体节点的处理方式不同，导致整体节点的节段模型计算结果与多尺度模型计算结果有所差异；对于复杂梁拱组合体系桥梁局部结构分析，多尺度模型分析方法能够较准确的描述其实际状态和刚度，具有较高的分析精度。

梁拱组合体系桥梁；整体节点；有限元；节段模型；多尺度模型；分析方法

近年来，随着我国大跨度钢桥建设事业的不断发展，整体节点技术得到广泛的应用[1−3]。桥梁跨径的增大，导致桥梁中整体节点的刚度和尺寸规模有增大的趋势。目前，国内学者对整体节点已经开展了部分研究，重点关注整体节点的工作性能和疲劳性能。其中，陈淮等[4]研究了郑州黄河公铁两用桥的整体节点的应力集中效应。张鹏举[5]对东新赣江桥的整体节点进行了受力分析，为设计提供依据。邓晓光等[6]对杨泗港长江大桥整体节点开展疲劳试验，并进行多轴荷载下整体节点的疲劳性能分析。实际上，大跨度桥梁整体节点与传统普通节点存在着较大的差异，尚缺乏大跨度桥梁整体节点设计计算的标准方法。目前，在进行局部结构有限元分析时常用的节段模型分析方法和多尺度模型分析方法，对于复杂梁拱组合体系桥梁结构中整体节点局部分析是否适用和各分析模型的结果差异还有待进一步研究。

1 工程背景

厦深铁路榕江特大桥主桥为梁拱组合体系桥梁，跨度布置为110+2×220+110 m。榕江特大桥主桥技术结构复杂，桥梁各节点均采用整体节点技术，整体节点的连接杆件较多，受力复杂，以E11整体节点为例，该节点连接了直腹杆和左、右弦杆以及上、下拱肋等10根杆件[7]。榕江特大桥主桥布置和E11节点位置如图1所示，E11节点结构尺寸如图2所示。

单位：m

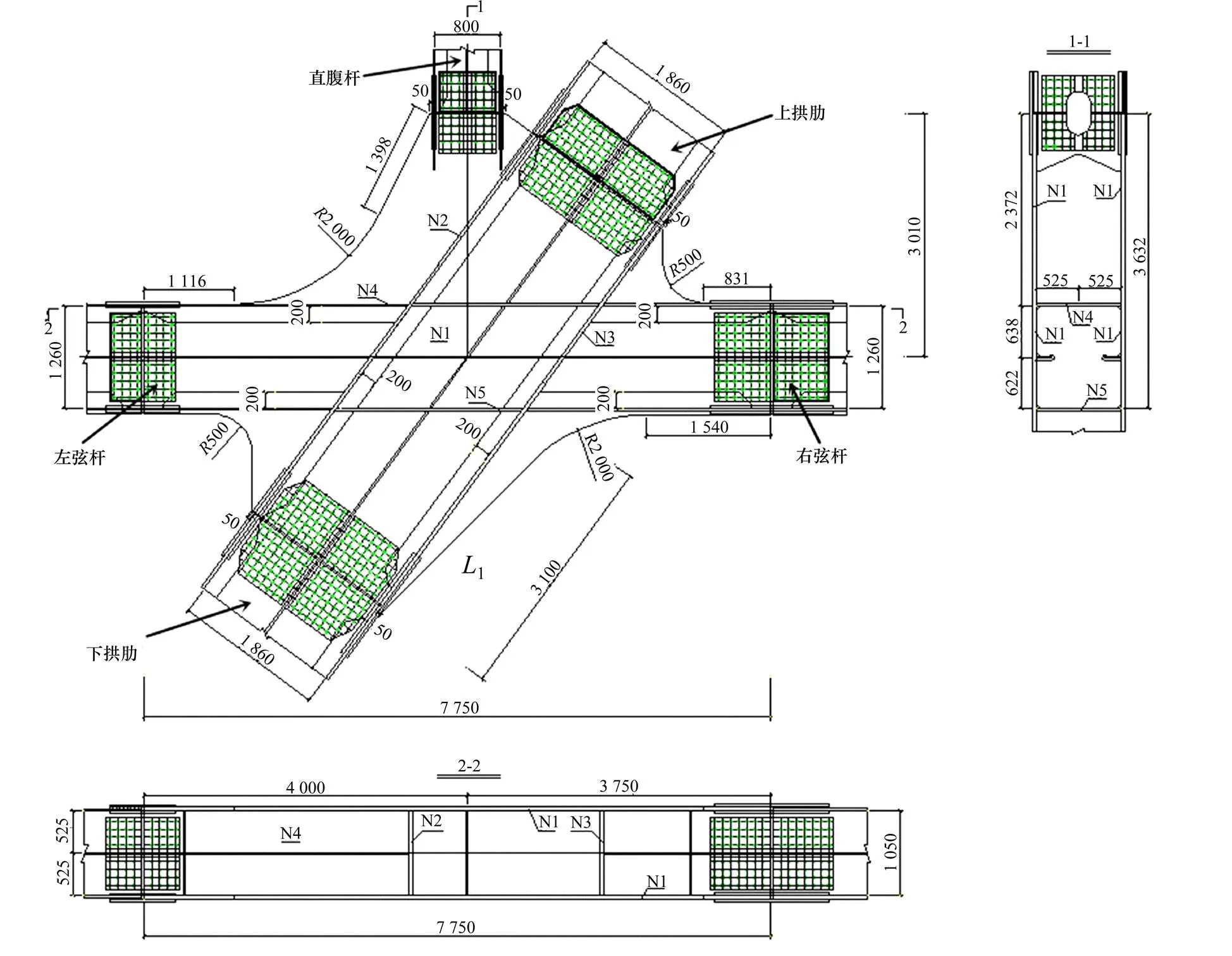
单位：m

2 桥梁有限元模型与整体节点有限元模型

2.1 桥梁有限元模型

在进行节段模型分析和多尺度模型分析前，应先进行全桥有限元分析。本文采用Midas Civil建立全桥有限元模型，由此计算得到对应荷载工况下各个整体节点位置相连杆件杆端的内力和变形。全桥有限元模型如图3所示，有限元模型中未考虑桥墩和桩基的影响，全桥主体结构均采用梁单元进行模拟，有限元模型中的约束条件根据实际桥梁结构的支座类型进行添加，该有限元模型共计7 225个节点，15 157个单元。

图3 榕江特大桥全桥梁单元模型

2.2 整体节点节段有限元模型

2.2.1 整体节点精细化节段模型

采用Midas FEA建立E11整体节点的精细化模型，模型由3节点和4节点板单元组成，最大边长不超过50 mm。在整体节点各个连接杆件杆端设置加长段，以消除因杆端施加荷载所引起的整体节点应力集中现象，各个杆件加长段的长度不小于相应杆件高度的5倍[8]。E11节点精细化节段模型如图4所示。

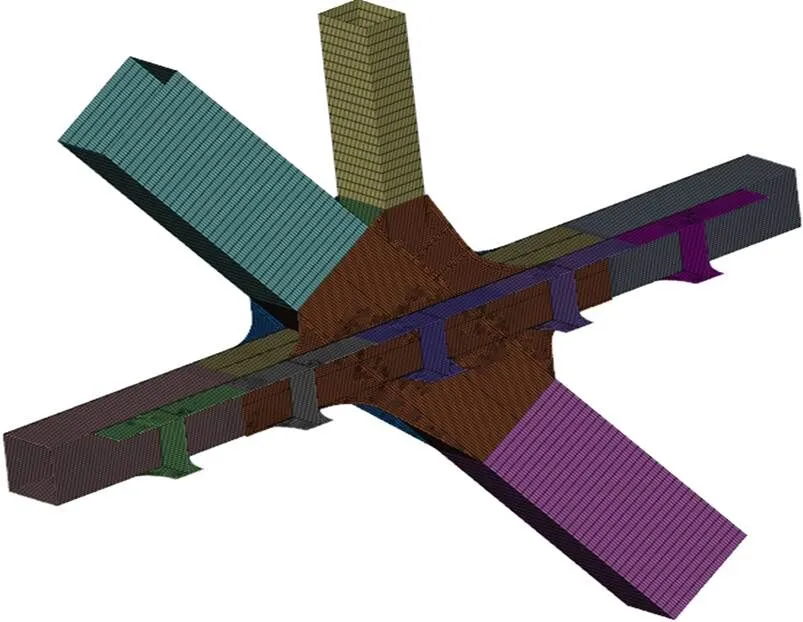
图4 E11节点精细化节段模型

2.2.2 整体节点节段有限元模型边界条件

节段模型的边界条件包括力边界条件、位移边界条件和混合边界条件等，由于力边界条件和位移边界条件概念清晰，实现容易，本文中予以应用并进行对比研究。基于力边界条件的节段模型和基于位移边界条件的节段模型是在整体节点精细化节段模型上，分别施加对应的力边界条件和位移边界条件得到的。在全桥有限元模型中得到的整体节点各相连杆件对应加长段长度末端位置节点的内力作为节段模型的力边界条件条件，施加于整体节点精细化节段模型各加长杆件端部。基于力边界条件的节段模型如图5(a)所示。为保证模型为几何不变体系，在节点板中心施加外部固定约束。同理，将全桥有限元模型中得到的整体节点各相连杆件杆端节点的内力换为变形，并将其作为位移边界条件施加于整体节点精细化模型时，可得到基于位移边界条件的节段模型，此处位移边界条件与力边界条件施加方式相同。基于位移边界条件的整体节点节段模型分别如图5(b)所示。

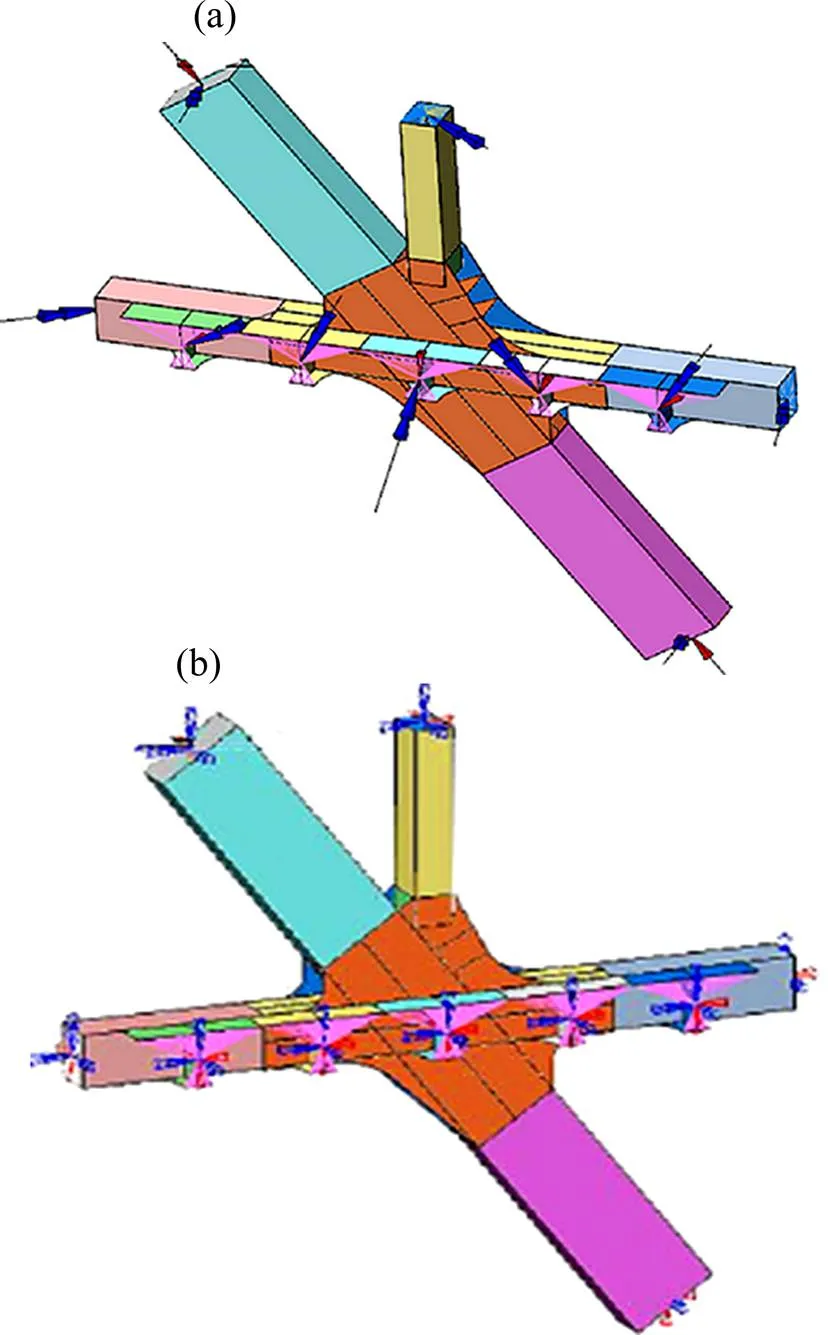
(a) 基于力边界条件的节段模型；(b) 基于位移边界条件的节段模型

2.3 整体节点多尺度有限元模型

多尺度模型是在同一个结构中同时使用多种尺度建立有限元模型[9−10]，多尺度模型相比节段模型模拟精度高，但建模复杂，计算量大。本文采用Midas FEA建立榕江特大桥E11整体节点的多尺度模型，即将全桥梁单元模型中与E11节点及加长段相同位置的杆件替换为上文中整体节点精细化节段模型。多尺度模型中整体节点相连各杆件加长段的板单元节点与其全桥梁单元模型中相邻的梁单元杆件的端节点通过刚性连接的形式实现力和变形的传递，由于整体节点存在杆件加长段，可认为刚性约束对整体节点受力无影响。刚性连接示意图如图6所示，图中板单元一侧对应为多尺度模型中包含的整体节点精细化节段模型，梁单元一侧对应为多尺度模型中包含的全桥梁单元模型中与整体节点相邻的梁单元模型，由此可认为，整体节点多尺度模型为全桥有限元模型对应整体节点位置替换为整体节点精细化节段模型得到的。

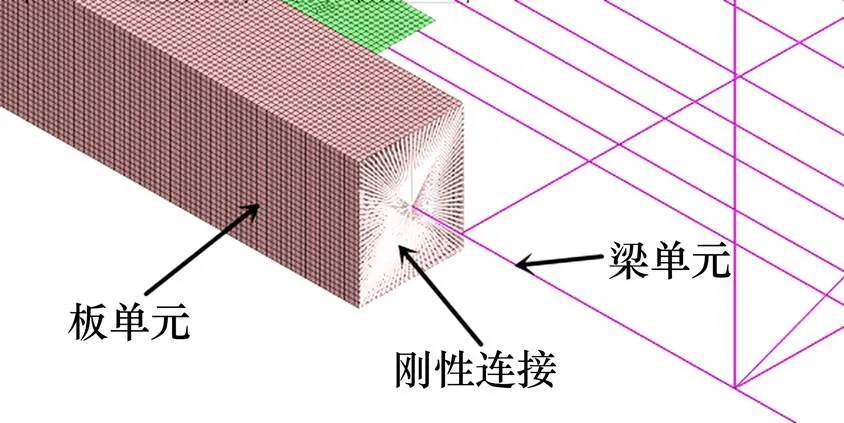
图6 刚性连接示意图

3 梁拱组合体系桥梁整体节点力学性能试验研究

3.1 试验工况

榕江特大桥E11整体节点力学性能试验的加载工况为双线最不利加载，具体为2节DF4型机车和4节满载K13型货车加载，按照运营中E11节点出现最不利工况的列车车辆位置进行加载，如图7 所示。

3.2 试验测点布置

通过采集E11整体节点几个典型部位的应变来研究其受力性能，并与前述各种有限元分析方法得到的理论值进行对比，通过试验结果来验证有限元分析方法的适用性。E11整体节点力学性能试验共布置14个应变测点，分别在整体节点的主板和上弦杆、下弦杆、拱肋、腹杆连接杆件处，测点布置位置和形式如图8所示。在试验过程中有5个测点失效，其余9个测点工作状态良好。

(a) 试验加载布置；(b) 有限元模型中的加载布置

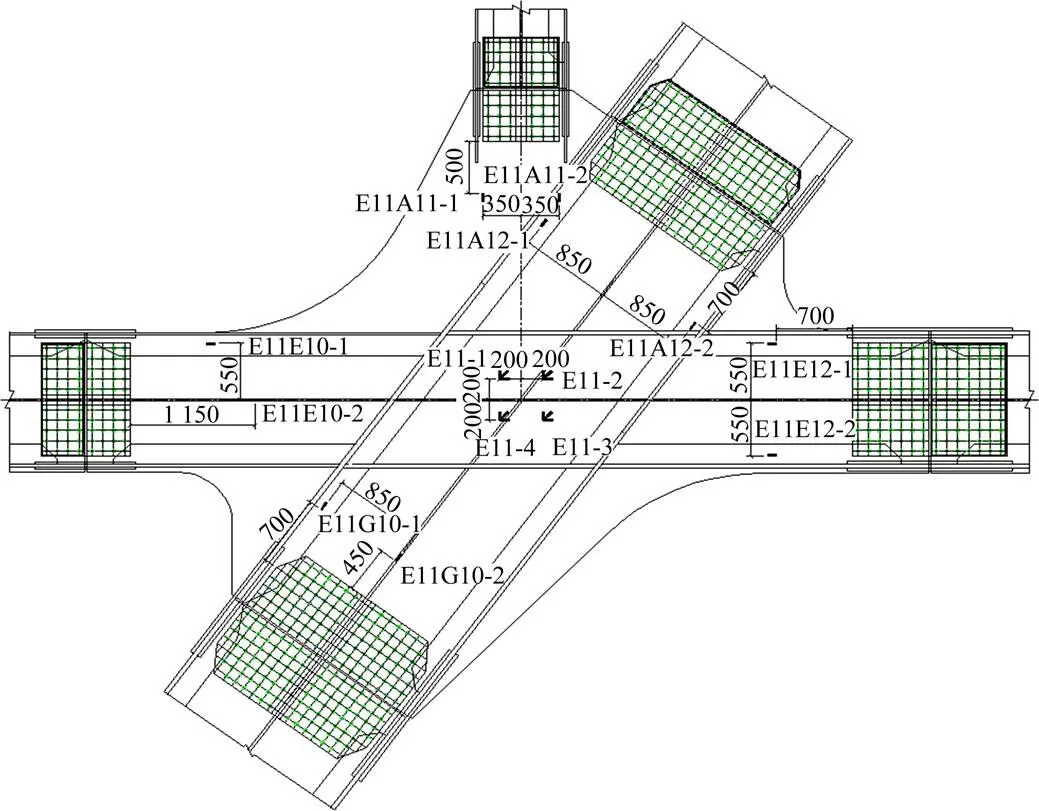
单位：mm

4 梁拱组合体系桥梁整体节点有限元分析方法对比分析

4.1 各有限元模型计算结果对比分析

由于试验测点有限，仅可得到整体节点测点位置的应力值，而整体节点结构的应力分布规律只能通过有限元分析才能得到。因此，本文中首先对各个有限元模型计算得到的应力分布规律进行对比研究，而后再将试验测点位置的应力值与各有限元模型计算结果进行对比研究，以期得到整体节点的应力分布规律和合适的有限元分析方法。各个有限元模型的荷载工况与试验加载工况相同，计算得到的E11整体节点的应力分布汇总于表1。

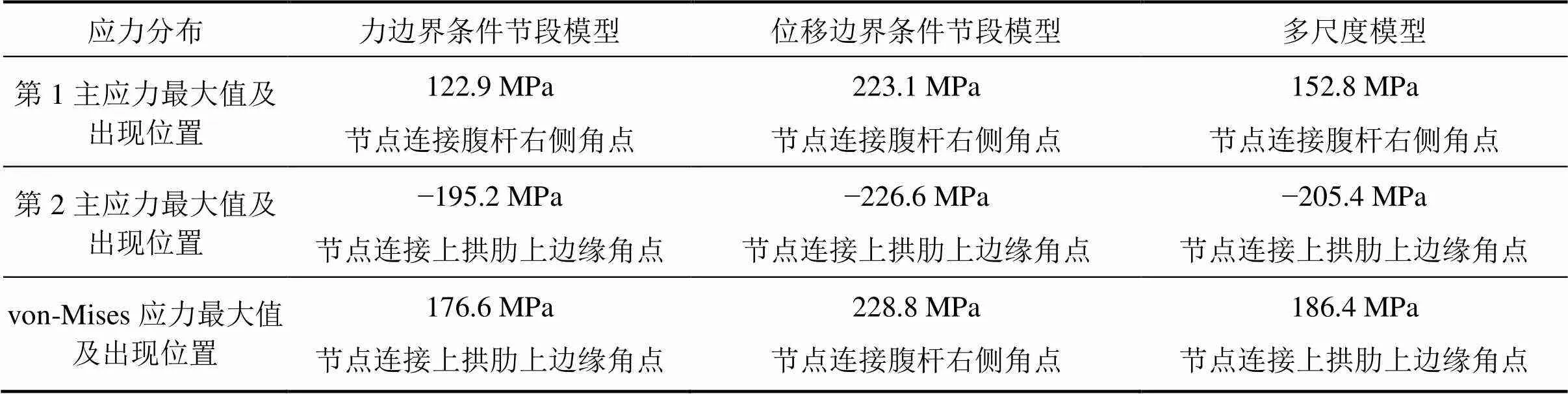
表1 E11整体节点应力分布

由表1可以看出，基于力边界条件的节段模型、基于位移边界条件的节段模型和多尺度模型计算得到的E11整体节点的各应力最大值出现位置是基本相符的，各应力最大值基本都出现在E11整体节点的连接上拱肋上边缘角点和腹杆右侧角点，在设计计算和施工运营时应特别注意。从全桥梁单元模型中提取整体节点节段模型边界条件时，无法考虑整体节点对全桥模型的影响，而多尺度模型中以板单元模拟了整体节点结构，这就导致基于力边界条件的节段模型和基于位移边界条件的节段模型以及多尺度模型的计算结果存在差异。

4.2 试验测试结果与有限元计算结果的对比分析

将上述各个有限元分析模型的理论结果与现场试验实测结果进行对比分析，具体如图9所示。

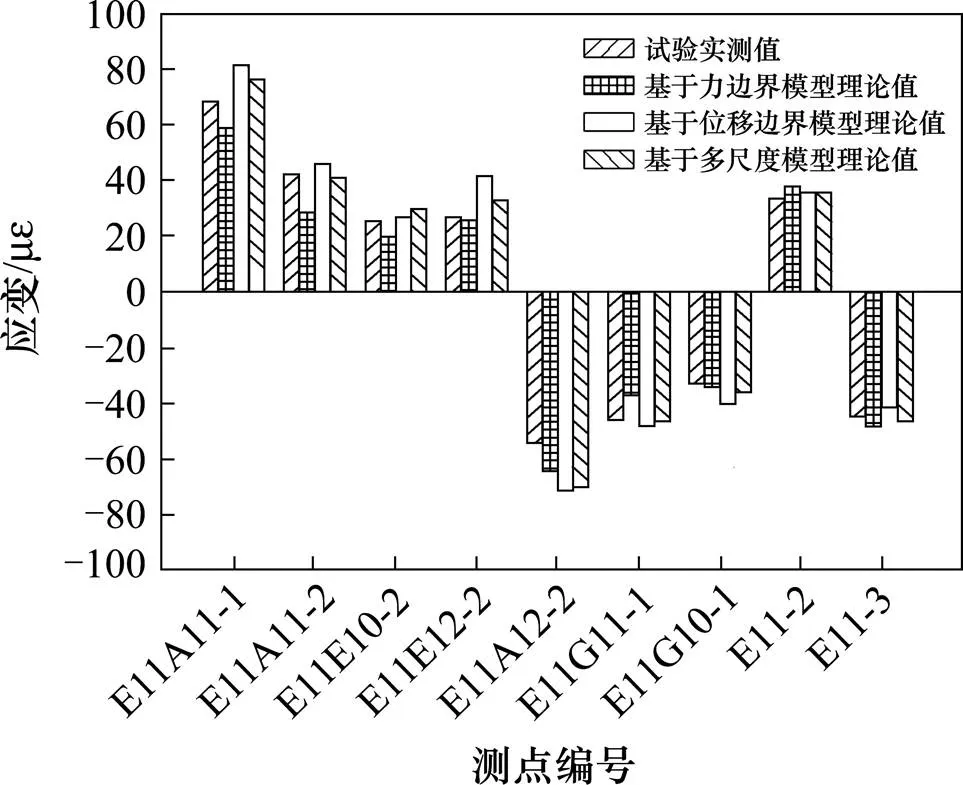
图9 实测应变值与有限元计算应变值对比

由图9可得，理论值与实测值相差不大，差异率大部分不超过20%。从全桥梁单元模型计算结果中取出整体节点的相关杆件的内力或位移，以此为边界条件开展整体节点的节段模型分析。由于整体节点的刚度很大，且全桥梁单元模型中节点的刚度是由刚性转角假定确定的，忽视了整体节点的实际状况，导致节段模型的边界条件存在误差，节段模型的计算精度取决于梁杆系模型中的刚性转角节点与实际节点刚度的差异。相比于节段模型，多尺度模型使用精细模型直接模拟复杂梁拱组合体系桥梁结构中的整体节点，一般能够较准确的描述实际结构和刚度，且有效避免从整体模型中提取节段模型边界条件带来的二次误差，因此，对于复杂梁拱组合体系桥梁整体节点分析，多尺度模型的计算结果具有较高的精度。

5 结论

1) 节段有限元模型和多尺度有限元模型的理论值与实测值基本吻合，差异率大都在20%以内。

2) 节段模型分析方法概念清晰，但由全桥模型提取力或位移作为节段模型的力或位移边界条件时存在二次误差，且全桥模型中难以准确模拟实际节点结构的刚度贡献。

3) 多尺度模型分析方法与节段模型分析方法相比，虽然建模工作量有所增加，但能够较准确的描述实际结构和刚度，避免二次误差的出现，确保模拟和计算的精度。由此，对于复杂梁拱组合体系桥梁结构的局部分析建议采用多尺度模型分析 方法。

[1] 程帅, 王会利, 韩加伦. 钢桁梁整体节点研究综述[J]. 钢结构, 2012, 27(6): 1−4. CHENG Shuai, WANG Huili, HAN Jialun. Review of the study of integral panel points of steel truss grider[J]. Steel Construction, 2012, 27(6): 1−4.

[2] 邢扬, 杨翠屏. 沪通长江大桥整体节点下弦杆制作工艺研究[J]. 钢结构, 2017, 32(4): 74−77. XING Yang, YANG Cuiping. Research on the manufacturing process of the lower chord with integral joints of Hutong Yangtze River bridge[J]. Steel Construction, 2017, 32(4): 74−77.

[3] 盛兴旺, 郑纬奇, 戴劲. 考虑整体节点刚域模拟影响的钢桁梁力学效应分析[J]. 桥梁建设, 2016, 46(6): 78−82. SHENG Xingwang, ZHENG Weiqi, Dai Jin. Analysis of mechanical effect of steel truss girder considering influences of rigid zone simulation of integral joints[J]. Bridge Construction, 2016, 46(6): 78−82.

[4] 陈淮, 李杰, 李谊修. 连续钢桁梁施工阶段整体节点局部应力分析[J]. 桥梁建设, 2011, 41(5): 21−25. CHEN Huai, LI jie, LI Yixiu. Local stress analysis of integral joint of continuous steel truss girder at construction stage[J]. Bridge Construction, 2011, 41(5): 21−25.

[5] 张鹏举. 四线双桁连续钢桁梁节点受力性能研究[D]. 成都: 西南交通大学, 2011. ZHANG Pengju. Study of mechanical behavior of joints of a continuous steel truss girder arranged with four tracks and double trusses[D]. Chengdu: Southwest Jiaotong University, 2011.

[6] 邓晓光, 刘沐宇, 史晶, 等. 大跨径双层悬索桥钢桁梁整体焊接节点疲劳分析与试验[J]. 中国公路学报, 2017, 30(3): 96−103. DENG Xiaoguang, LIU Muyu, SHI Jing, et al. Fatigue analysis and test on integral welded joint at steel truss girder of long-span double deck suspension bridge[J]. China Journal of Highway and Transport, 2017, 30(3): 96−103.

[7] 戴劲. 钢桁梁柔性拱组合体系桥节点板受力性能分析与试验研究[D]. 长沙: 中南大学, 2014.DAI Jin. Study on mechanical behavior and experiment of integral joints in combination structure of steel truss girder and flexible arch[D]. Changsha: Central South University, 2014.

[8] 宋少云, 尹芳. 有限元网格划分中的圣维南原理及其应用[J]. 机械设计与制造, 2012(8): 63−65. SONG Shaoyun, YIN Fang. Sain Vaint principle of meshing in finite element method and its application[J]. Machinery Design & Manufacture, 2012(8): 63−65.

[9] 王会利, 殷洪建, 秦泗凤. 基于多尺度有限元的钢桁架整体节点疲劳性能分析和试验研究[J]. 世界桥梁, 2016, 44(6): 46−49. WANG Huili, YIN Hongjian, QIN Sifeng. Analysis of fatigue performance of steel truss girder integral panel points based on multi-scale finite element and experimental study[J]. World Bridge, 2016, 44(6): 46−49.

[10] 周萌, 聂建国. 自锚式悬索桥主缆锚固区多尺度建模方法[J]. 桥梁建设, 2014, 44(1): 11−17. ZHOU Meng, NIE Jianguo. Multi-scale modeling method for main cable anchorage zone of self-anchored suspension bridge[J]. Bridge Construction, 2014, 44(1): 11−17.

Comparative study on finite element analysis methods of integral node in combinatorial bridge with beam and arch

YANG Ying1, SHENG Xingwang1, ZHENG Weiqi1, DAI Jin1, 2

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Hunan Hydro & Power Design Institute, Changsha 410000, China)

The finite element models of integral joint plate in combinatorial bridge with beam and arch were established based on the method of segmental model and multi-scale model. Combined with the static loading test, the mechanical performance of the integral joint plate in each calculation mode was compared and analyzed. The research results show that the difference rate of the calculated value and measured value is mostly within 20%; due to the different processing modes of the integral node, the calculation result of the integral node's segmental model is different from that of the multi-scale model; compared with segmental model, the multi-scale model can describe the actual state and stiffness of complex structures in combinatorial bridge with beam and arch more accurately, and has higher analytical accuracy.

combinatorial bridge with beam and arch; integral node; finite element method; segmental model; multi-scale model; analysis method

10.19713/j.cnki.43−1423/u.2019.04.016

U24

A

1672 − 7029(2019)04 − 0953 − 06

2018−05−14

中南大学中央高校基本科研业务费专项资金资助项目(2017zzts155)；中国铁路总公司科技研究开发计划项目(2015G001-G)

郑纬奇(1991−)，男，山东淄博人，博士研究生，从事大跨度桥梁结构行为及无砟轨道理论研究；E−mail：wqzheng@csu.edu.cn

(编辑 涂鹏)