基于修正Stribeck模型的摩擦补偿策略

陈 琳，梁耘涌，贺飞翔，黄旭丰，张 旭，潘海鸿

(1. 广西大学，南宁 530004； 2. 广西制造系统与先进制造技术重点实验室，南宁 530004)

0 引 言

摩擦广泛存在于数控、机器人、印刷、包装和医疗等机电系统，其容易导致系统低速运行不平稳，停止时出现定位误差以及极限环现象[1]。通过引入摩擦补偿可以较好地解决以上问题，但同时也容易出现摩擦过补偿现象，同样会引起极限环振荡及系统抖动[2-4]。为此，国内外学者对摩擦作了大量研究，目前已提出30多种摩擦模型[5]，其中，Stribeck摩擦模型因其对摩擦特性描述相对全面和准确，模型相对简单，是研究较多的一种摩擦模型，且在工程上应用比较广泛。

为改善Stribeck摩擦补偿效果，向红标等[6]提出了基于Stribeck模型的自适应滑模补偿控制方法，有效提高系统准确度和动态跟踪性能，抑制伺服系统的摩擦干扰，但滑模控制容易使系统发生抖振。付永领等[7]提出模糊算法整定Stribeck摩擦模型状态参数；张来福等[8]提出利用遗传算法辨识出摩擦参数，使得辨识出的摩擦参数和实际参数尽可能接近，然后将辨识出的摩擦参数加入到伺服系统补偿控制中，通过提高摩擦模型参数辨识精度，改善了摩擦补偿效果，但存在算法复杂、运算费时的不足，且以上研究均未考虑摩擦过补偿问题[9]。Cong S[10]等根据平台位置及速度正反方向，提出一种改进Stribeck摩擦补偿策略用于降低过补偿影响，但需要辨识12个模型参数，模型过于复杂。晋超琼[9]和周旋[11]通过添加扰动观测器观测并补偿系统中过补偿的摩擦，但扰动观测器需要对系统标称模型求逆，容易引入微分测量噪声。

针对上述问题，本文提出了一种适用于低速换向的修正Stribeck摩擦模型，该模型采用位置信号微分滤波滞后的速度作为输入，使其与系统实际速度同相位，通过在系统速度过零点附近出现过补偿的速度段，引入修正因子，修正补偿值，削弱过补偿效果，从而减小系统过零点速度波动及跟踪误差，提高运动控制系统低速运行性能。

1 Stribeck摩擦补偿策略原理

基于运动控制层研究摩擦补偿算法，摩擦补偿点选择运动控制器层，采用轴运动控制器的速度控制器输出作为摩擦补偿信号注入点，并选择基于Stribeck模型摩擦补偿方法，如图1所示。

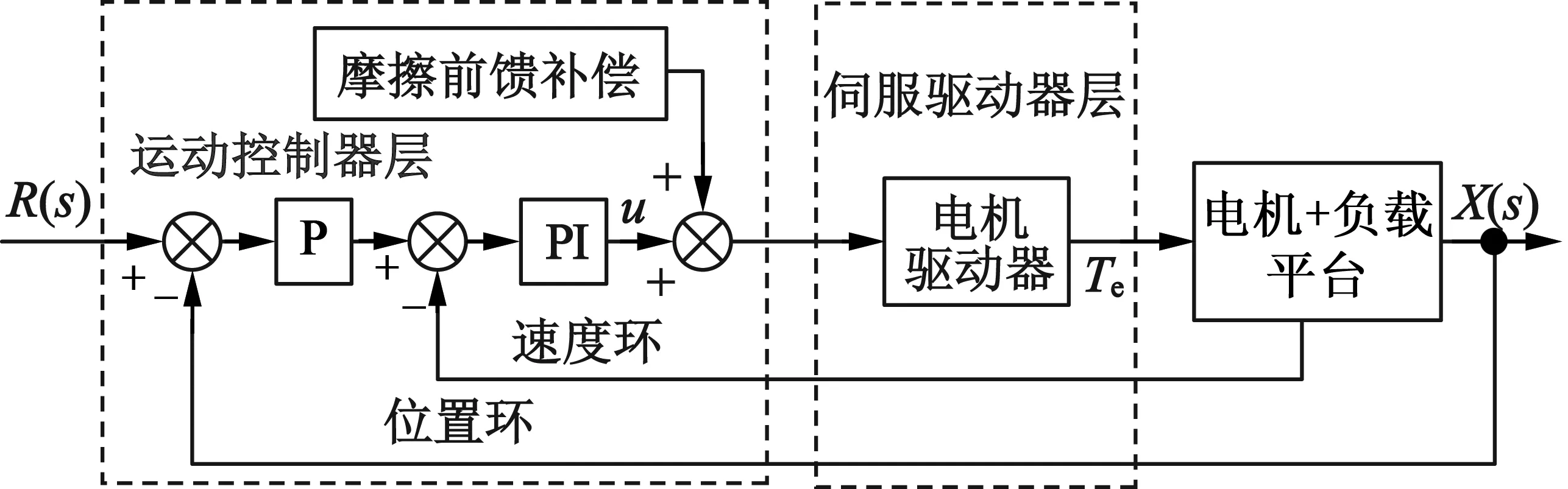
图1 摩擦补偿原理框图

1.1 Stribeck摩擦模型

Stribeck摩擦模型中摩擦力矩与转速关系如下：

Tf(v)=[Tc+(Ts-Tc)e-(v/vs)2]sgn(v)+Bvv(1)

式中：v为旋转角速度；Ts为最大静摩擦力矩；Tc为库伦摩擦力矩；Bv为粘性摩擦系数；vs为Stribeck速度。

1.2 传统Stribeck摩擦模型补偿效果仿真

对轴运动控制系统进行摩擦补偿仿真，首先需对轴运动控制系统建模。一阶模型有良好的抑制扰动作用，而且由于阶次低，不会过多放大测量误差。将速度环被控对象简化为一阶惯性环节[12]，轴运动控制系统可简化为图2的模型。

图2 轴运动控制系统简化模型

图2中，Pref为给定位置，Kpp为位置控制器比例增益，ωref为位置控制器输出，Kvp，Kvi为速度PI控制器比例增益及积分增益，Kt为转矩系数，J为转动惯量，B为粘性摩擦系数，ωout为电机输出转速，Pout为电机输出位移。

模型中电流环和电机部分参数参考文献[7]，而速度环PI参数Kvp，Kvi与位置环P参数Kpp则采用MATLAB/Sisotool工具箱进行整定[13]，参数如表1所示。

表1 轴运动控制系统简化模型参数

基于图2建立的系统摩擦扰动仿真模型如图3所示，其中摩擦扰动采用基于Stribeck摩擦模型的摩擦扰动，依据文献[14]的参数辨识方法辨识获得的摩擦模型参数如表2所示。由于摩擦对系统低速运行平稳性影响较为明显，给定较小的正弦位置信号sin(0.4πt)，通过观测系统速度和位移曲线研究系统低速换向时摩擦特性。摩擦仿真模型在正弦激励下位置响应情况如图4所示，速度响应情况如图5所示。由图4、图5可知，由于摩擦影响，系统在速度过零点处速度无法及时响应，导致正弦位置响应峰值处出现削顶现象，在速度响应曲线上则表现为速度死区现象。

图3 摩擦扰动仿真模型

图3中，vel为反馈速度，Tf摩擦扰动转矩。

表2 Stribeck摩擦模型参数*

*表中参数为松下100 W电机空载运行时的参数

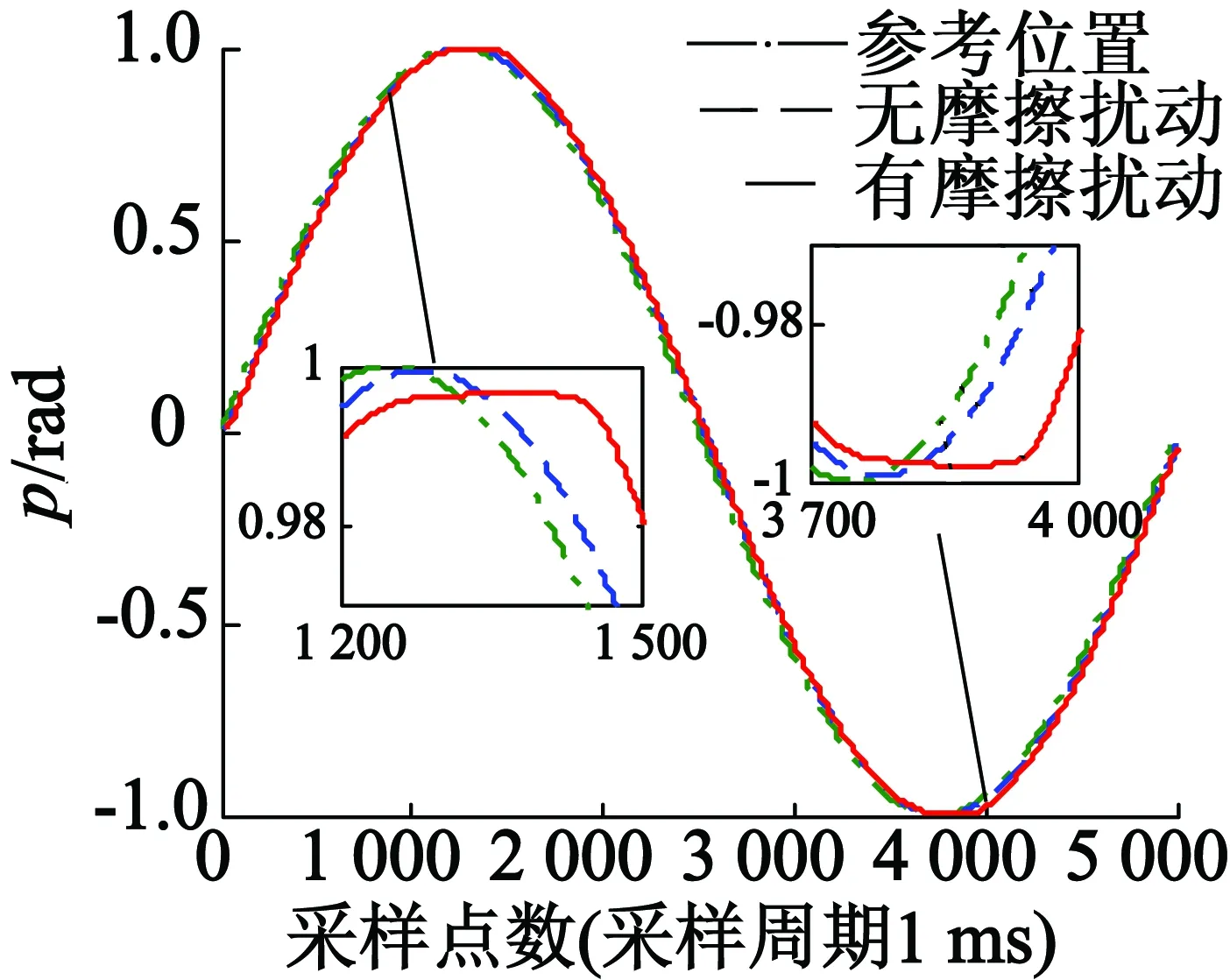
图4 有无摩擦扰动下的位置换向曲线

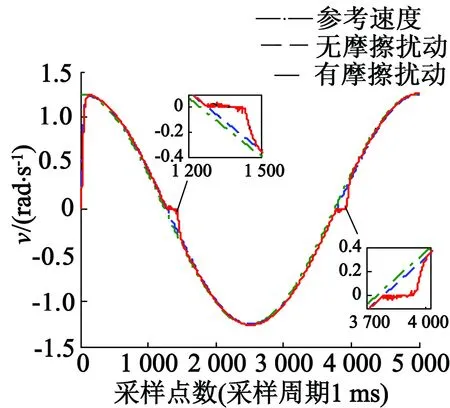
图5 有无摩擦扰动下的速度换向曲线

为减小摩擦对系统运动性能影响，采用Stribeck模型进行摩擦补偿，基于图3的摩擦仿真模型在0.001～60 rad/s速度范围内取不同速度值进行匀速运动，采用MATLAB/Curve Fitting对速度和摩擦扭矩进行Stribeck拟合，辨识获取Stribeck模型参数如表3所示。

表3 Stribeck摩擦模型辨识参数

建立如图6所示的轴运动控制系统Stribeck摩擦补偿仿真模型，采用表3的模型参数进行摩擦补偿实验。摩擦补偿前后系统位置换向曲线如图7所示，速度换向曲线如图8所示。

图6 摩擦补偿仿真模型

图6中，vel为反馈速度，Tf摩擦扰动转矩，pos为位置指令，Tf_comp为摩擦补偿转矩。

由图7、图8可知，摩擦补偿后系统在速度过零处响应加快，对应摩擦扰动下速度死区现象得到消除，因此，Stribeck摩擦补偿可以消除系统速度过零点处因摩擦导致系统速度无法及时响应的情况。但是因为摩擦补偿采用的模型与摩擦扰动采用的摩擦模型存在差别，出现摩擦过补偿、速度突然反向且存在波动现象，导致正弦位置曲线峰值出现波动。

图7 摩擦补偿后位置换向曲线

图8 摩擦补偿后速度换向曲线

2 修正Stribeck模型后的补偿仿真

针对Stribeck摩擦补偿导致系统过零点处速度换向存在较大波动，从而导致位置响应出现波动的问题，经过分析，主要有如下两方面原因：一是系统滞后，二是系统摩擦模型存在误差。系统滞后导致基于参考速度的Stribeck摩擦补偿在实际速度未达到零时，摩擦补偿反向，而模型误差进一步加大速度过零处点的速度波动。针对系统滞后的问题，可以将Stribeck摩擦补偿输入参数的参考速度更改为系统实际速度，但是由于存在测量噪声，实际速度在零速附近波动较大，对系统速度过零点附近运行情况并没有改善，反而增加系统速度波动。而采用经过滤波滞后的参考速度作为Stribeck摩擦补偿输入，不仅可以与实际速度同相位，而且系统过零点附近无明显速度波动。针对系统摩擦模型存在的误差，可通过对Stribeck模型进行修正来解决，如图9所示，对零速附近的摩擦补偿进行修正。

图9 修正Stribeck摩擦仿真模型

Stribeck摩擦模型修正后表达式如下：

(2)

式中：m为速度范围，根据传统Stribeck模型进行摩擦补偿时出现过补偿现象的速度点附近选取；k为修正因子，k<1，通过试凑法选择最优值。

对修正Stribeck摩擦模型补偿效果进行仿真实验验证，系统正弦位置换向曲线如图10所示，速度换向曲线如图11所示，将无摩擦补偿与有摩擦补偿以及修正摩擦补偿三者速度误差与跟踪误差进行对比，如图12、图13所示。

图10 修正摩擦补偿后系统位置换向曲线

图11 修正摩擦补偿后系统速度换向曲线

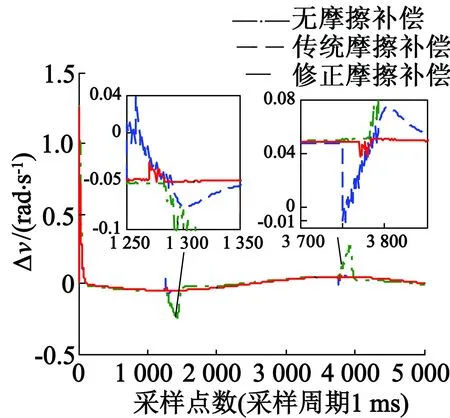
图12 有无摩擦补偿情况下的速度换向误差曲线

图13 有无摩擦补偿情况下的位置换向误差曲线

由图12、图13可知,采用修正Stribeck摩擦补偿后,仿真模型在速度过零点处速度波动明显减小，无摩擦补偿位置响应削顶现象和有摩擦补偿时速度波动均得到抑制。其中,仿真模型在速度过零点处速度波动情况如表4所示，采用修正Stribeck摩擦补偿方法，在系统速度过零点处最大速度波动，比无摩擦补偿时减小80%以上，比传统Stribeck摩擦补偿减小49%以上。

表4 速度过零处速度波动值

3 实验与结果分析

为验证本文的修正Stribeck摩擦模型补偿效果，在单轴运动控制系统配置位置环、速度环，驱动器配置为转矩控制。实验平台实物图如图14所示。

图14 单轴运动控制系统实验平台

轴运动控制器相关控制参数选择：位置控制器比例系数Kpp=15，速度控制器比例系数Kvp=150，速度控制器积分系数Kvi=0.8。

Stribeck模型参数辨识结果如表5所示。

表5 Stribeck摩擦模型参数辨识结果

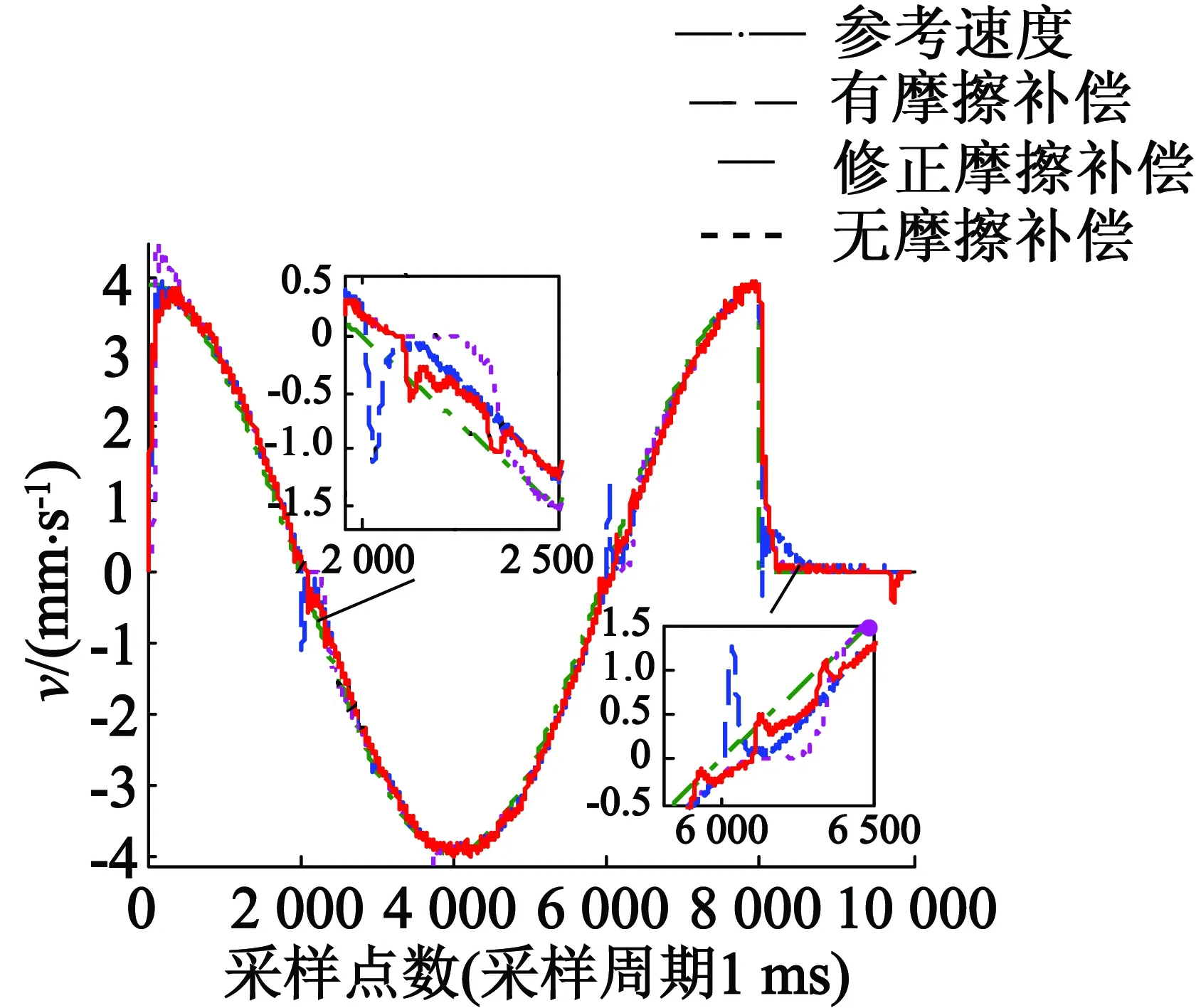
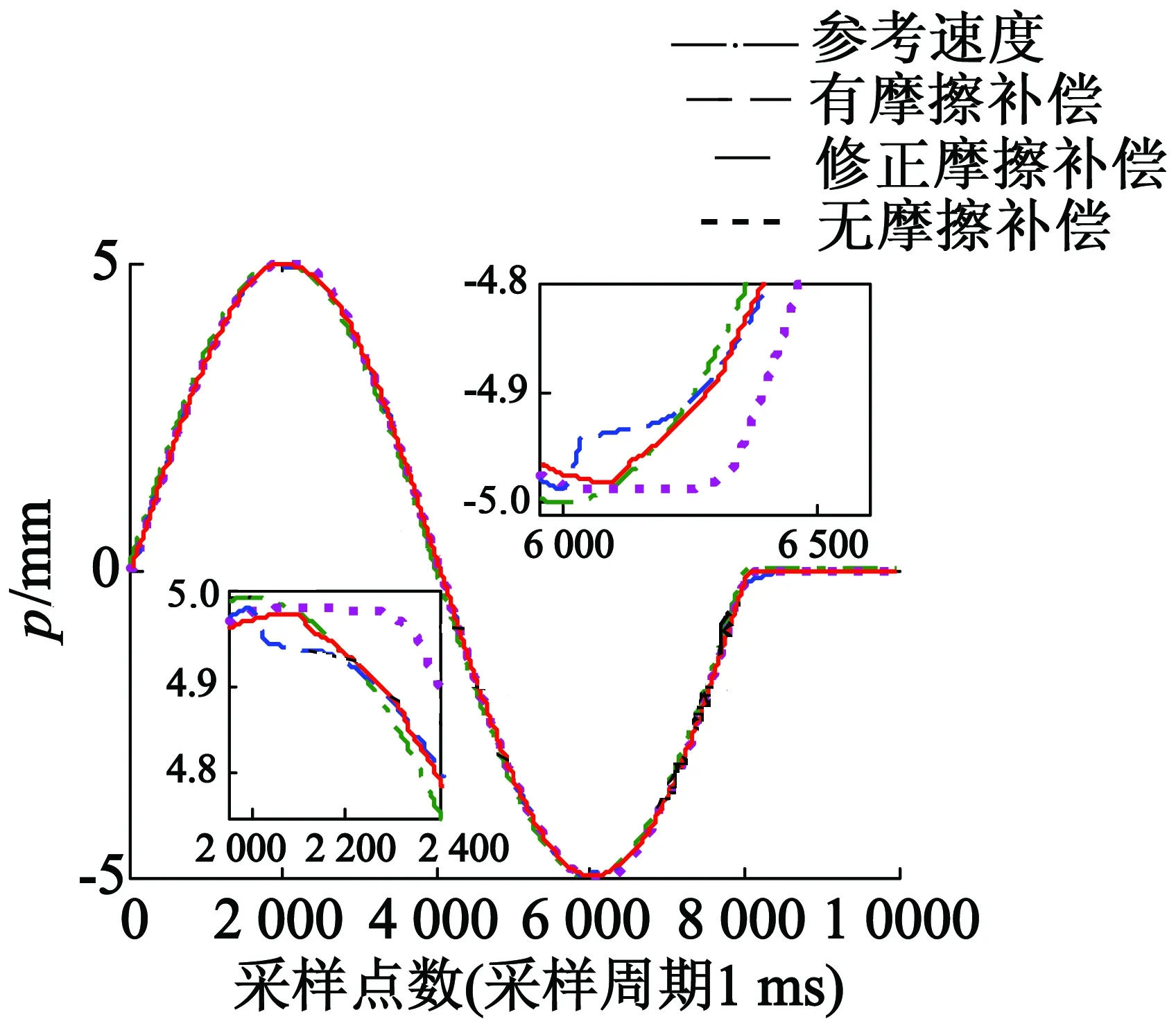
分别对平台进行幅值为5 mm和10 mm的正弦位置响应实验，对参考速度滤波使之与实际速度同相位。通过反复实验对Stribeck摩擦模型进行如表6所示的修正，有无摩擦补偿系统的实际速度换向曲线如图15(a)、图16(a)所示，系统的实际位置换向曲线如图15(b)、图16(b)所示。

表6 Stribeck摩擦模型修正参数表

系统在无摩擦补偿、有摩擦补偿和修正摩擦补偿之后，速度过零点处的速度波动如表7所示，在修正摩擦补偿下系统速度过零点处的速度误差波动最小，即速度偏离参考速度最小。幅值5 mm正弦位置信号下，修正摩擦补偿后速度由正变负过零点附近的速度误差波动由无摩擦补偿时的-1.99mm/s减小至0.65 mm/s，减小67.34%；修正摩擦补偿后的速度波动比传统摩擦补偿后减小63.48%。而速度由负变正过零点附近的速度误差波动由无摩擦补偿时的1.88 mm/s减小至-0.58 mm/s，减小69.15%；修正摩擦补偿后的速度波动比传统摩擦补偿后减小71.71%。幅值10 mm正弦位置信号下，速度由正变负过零点附近，速度误差波动由无摩擦补偿时的-2.15 mm/s减小至修正摩擦补偿后的0.71 mm/s，减小66.98%；修正摩擦补偿后的速度波动比传统摩擦补偿后减小72.70%。而速度由负变正过零点附近的速度误差波动由无摩擦补偿时的2.48 mm/s减小至修正摩擦补偿后的-0.69 mm/s，减小72.18%；修正摩擦补偿后的速度波动比传统摩擦补偿后减小64.62%。

(a) 速度换向曲线

(b)位置换向曲线

(c)速度换向误差曲线

(d)位置换向跟踪误差曲线

(a) 速度换向曲线

(b)位置换向曲线

(c)速度换向误差曲线

(d)位置换向跟踪误差曲线

表7 速度过零点处的速度波动

采用修正Stribeck模型的摩擦补偿，可以有效减小速度换向时的速度误差，并且由图15(a)和图16(a)可知，修正摩擦补偿下系统的位置响应在速度过零点处更加平滑，在图15(c)、图15(d)和图16(c)、图16(d)中也可以发现，系统速度过零点处的速度误差及跟踪误差有明显的减小。

4 结 语

针对运动控制系统低速换向运行时Stribeck摩擦模型的过补偿现象，本文设计了修正Stribeck摩擦模型。在传统Stribeck摩擦模型基础上，首先对参考速度进行滤波使其与反馈速度同相位后作为模型输入速度，然后对过补偿的速度段的摩擦力乘以一个修正系数，有效地改善了摩擦过补偿现象，提高了系统响应速度，从而最终减小系统速度换向处的跟踪误差。