基于波面分解的跨海桥梁下部结构波浪荷载计算方法
魏 凯,张家瑞,梁春明
(1.西南交通大学土木工程学院桥梁工程系,成都 610031; 2.中铁二院工程集团有限责任公司,成都 610031)
近年来,跨海大桥在我国沿海地区大量修建[1,2]。以在建的平潭公铁两用大桥为例,该桥所处的平潭海峡,属于世界三大风口海域之一,风大浪高、海况复杂,巨大的波浪作用严重威胁跨海大桥的建设和运营安全[3-5]。在实际桥梁工程中,结构所受的波浪荷载很难直接测量,通常采用声学波浪仪或浮标等设备对桥梁所在海域的波面变化情况进行观测,根据实测数据推算相应海域的波浪环境参数,进而计算结构受到的波浪荷载。目前,通过波面得到波浪荷载的主要方法有:代表波法、谱分析法等[6]。代表波法是对波面实测数据进行统计分析,提取具有统计特征的波高和周期,然后由此构造规则波计算波浪荷载[7]。然而,代表波法不能反映波浪荷载随时间的变化规律。谱分析法则是将波面时程转化为频谱模型,通过谱分析方法计算波浪荷载。高加云对比讨论了不同波浪谱数学模型对波浪场、风浪场的模拟精度[8],贺成柱基于SZF型波浪浮标数据,详细研究了常用海浪功率谱以及海浪方向谱的参数估计方法[9],高加政等针对江苏沿海的波浪场采用基于不同波浪谱的SWAN模型进行模拟,结果发现采用实测谱的模拟结果与实测值更为接近[10]。虽然谱分析法能够得到波浪荷载随时间的变化,但不同海域的谱模型存在明显差异,对于缺乏长期观测的海域,缺乏适用性[11]。
综上,如果能够基于波高仪等观测到的波面数据直接计算作用于跨海桥梁下部结构的波浪荷载,就可以实现对波浪荷载的实时监控,这对跨海大桥的设计、建造以及运营维护具有重要的现实意义和实用价值。李玉成、康海贵等学者先后基于对称和反对称滤波器原理,由已知波面过程线计算速度和加速度过程线,从而计算波浪水流力[12-13]。采用类似思路,本文提出一种基于波面分解的跨海桥梁下部结构波浪荷载计算方法。通过与理论、试验、数值模拟进行对比,验证方法的适用性和准确性。
1 基于波面分解的波浪荷载计算理论
1.1 基本假设
以桥梁圆柱桥墩为例,推导基于波面分解的波浪荷载计算方法。为便于理论推导,忽略结构与波浪场的相互影响,仅关注小尺度结构。
1.2 波面分解

(1)
式中,Ai、ωi、εi分别为第i个组成波的振幅、圆频率、相位;t为时间。

图1 波面分解
1.3 波浪速度场与加速度场重构
根据线性波理论,式(1)中第i个线性规则波的水平速度vi、加速度ai可根据式(2)求解
(2)

将所有m个线性规则波的水平速度、加速度时程线性相加,得到波面时程η(t)对应的水质点水平速度v和加速度a
(3)
1.4 结构波浪荷载
对于小尺度圆柱桥墩,根据Morison方程[14],作用于直径D,长度ds圆柱上的波浪荷载dF如式(4)所示
(4)
式中,ρ为水的密度;CD为拖曳力系数;CM为惯性力系数。
将式(3)代入式(4),并沿水深z方向积分即可得到桥墩墩底剪力F与墩底弯矩M,如式(5)所示。由此可见,波浪荷载与波浪的速度、加速度密切相关,波浪速度、加速度的准确重构是进行波浪荷载合理计算的前提。所以,在对比本文方法与理论和试验结果时,主要对比分析的要素为水质点的速度和加速度,而在对比本文方法与数值模拟结果时,主要对比分析的要素为波浪作用产生的墩底弯矩和剪力。
(5)
2 波面分解的理论验证
本节以经典波浪理论为参照,对本文方法进行验证。主要对比要素为根据波面分解重构得到的水质点速度与加速度。
2.1 波浪速度与加速度理论值
线性规则波的波面时程、速度与加速度理论值根据式(6)求解
(6)

Stokes五阶波的波面时程、速度与加速度理论值根据式(7)求解
(7)
式中,c为波速,系数λ1,…,λ5的计算公式较为复杂,具体可参阅文献[15]。
不规则波根据线性叠加法生成,其波面时程、速度与加速度理论值根据式(8)求解
(8)

2.2 规则波
取波高1.6 m,周期10 s,水深10 m为规则波参数,分别根据式(6)~式(7)计算线性波与Stokes五阶波的波面时程、不同深度处水质点的水平速度、加速度时程。根据上述波面时程数据,应用本文方法,即式(1)~式(3)对波面进行分解,得到不同深度处水质点的水平速度与加速度。
图2依次给出了线性波和Stokes五阶波水平速度、加速度最大值沿水深方向的分布。由图2可知,对于线性波,本文方法的结果与理论值吻合较好;对于Stokes五阶波,在水下较深处,本文结果与理论值吻合较好,但本文方法在波面处的速度和加速度偏大近8%。差异较大的原因主要是本文方法根据线性波理论计算水质点速度,而Stokes五阶波属于非线性波,本文方法未考虑非线性波水质点速度计算中的高阶成分。

图2 规则波验证
2.3 不规则波
取有效波高15 m,谱峰周期13.73 s,水深50 m作为不规则波参数,采用JONSWAP谱[16]根据式(8)计算波面时程,水平速度、加速度时程理论值。不规则波面如图3所示。根据该波面时程,应用本文方法,即式(1)~式(3)计算相应的速度、加速度。图4给出了水平速度、加速度的理论值和本文方法值对比图。由图4可知,在任意深度本文方法值与理论值基本一致,说明本文方法可以有效根据不规则波面求解水平速度和加速度场。
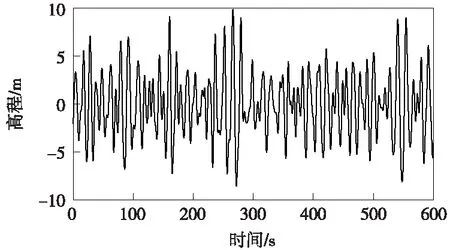
图3 JONSWAP谱生成的不规则波面
3 波面分解的试验验证
3.1 试验工况
为进一步验证本文方法计算水质点运动速度的准确性,依托西南交通大学深水大跨桥梁实验室中型波流水槽开展相关试验研究。该波流水槽长60 m,宽2 m,高1.8 m,采用推板造波系统造波,可根据水深、波高、周期、波浪类型等参数,通过计算机控制推波板的往复运动,生成指定的波浪。消波区采用斜坡消散造波机产生的波浪,避免反射的波浪对测量造成干扰。试验过程中,利用造波机在水槽中生成如下试验波浪工况:

图4 不规则波验证(黑色实线为波面)
(1)规则波,水深0.6 m,波高0.09 m,周期1 s;
(2)不规则波,水深1 m,有效波高0.1 m,谱峰周期1.5 s,采用JONSWAP谱。
水槽中的波面数据采用电阻式波高仪进行实时采集,采样频率20 Hz;水面下0.2 m处水质点的水平速度时程数据采用多普勒流速仪采集,采样频率100 Hz,并以此作为波浪速度的试验值。测试过程中,波高仪与多普勒流速仪由计算机控制,从而实现数据的同步实时采集。试验仪器的布置如图5所示。
3.2 方法验证
试验实测得到的水质点速度时程与本文方法结果的对比如图6所示。由图6可知,无论是规则波还是不规则波,本文方法值与试验值吻合较好,其中,对于不规则波,在速度峰值处试验值比本文方法值偏大。
将试验和本文方法得到的水平速度时程分别进行傅里叶变换,得到相应的速度谱,如图7所示。由图7可知,对于规则波,本文方法与试验的速度谱吻合较好;对于不规则波,本文方法整体上与试验值相吻合,但在谱峰处偏低(如图中方框所示),这解释了二者在时程上的差异。

图5 波浪水槽试验
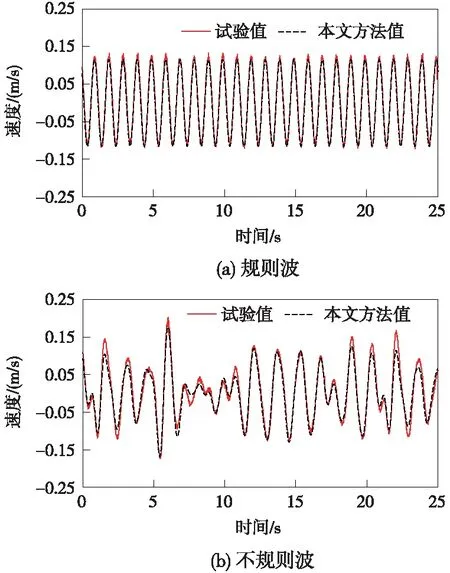
图6 水质点速度时程对比

图7 水质点速度频谱
4 圆柱桥墩波浪荷载算例
本节采用算例的形式对比了数值分析与本文方法得到的波浪作用下圆柱桥墩的墩底弯矩和剪力。
采用海洋工程分析中常用的商业计算软件USFOS建立圆柱的三维数值模型,如图8所示。该软件首先以表1中的有效波高和谱峰周期为输入参数,根据JONSWAP谱生成不规则波面,如图9所示,采用Morison方程直接计算波浪作用下圆柱墩底弯矩和剪力[17]。作为对比,对于图9所示的不规则波面时程,根据本文方法,应用式(1)~式(5),依次通过波面分解、速度和加速度场重构和波浪荷载计算3个步骤计算桥墩受到的波浪荷载。
图10给出时间150~250 s的墩底剪力和墩底弯矩时程对比。表2给出了图10中时间190~205 s之间4个墩底剪力、弯矩峰值点的对比情况。由图10和表2可知,本文方法得到的墩底剪力和墩底弯矩与数值模拟结果吻合良好。与数值模拟相比,本文方法得到的墩底剪力及墩底弯矩均较大,墩底剪力相对误差在3%左右。而墩底弯矩相对误差在8%左右,满足工程应用的精度要求。由此可知,基于波面分解的波浪荷载计算方法是可行的。同时,由于本文方法无需任何波浪数值分析软件,只需波面时程就可以进行波浪荷载估计,具有较高的计算效率。
虽然本文仅以圆柱桥墩为算例进行讨论,但本文方法同样适用于矩形桥墩、群桩等结构,只要根据规范[18-19]、试验[13,20]等得到对应的水动力系数CD、CM,就能够应用本文方法计算这些结构的波浪荷载。

图8 软件USFOS中数值模型

参数数值参数数值桥墩直径/m3谱峰周期/s13.73拖曳力系数1.2水深/m30惯性力系数2.0计算时长/s350有效波高/m6

图9 由JONSWAP谱生成的不规则波面

图10 墩底剪力、弯矩时程对比

剪力/kN数值模拟本文方法值相对误差/%弯矩/(kN·m)数值模拟本文方法值相对误差/%651.60677.503.9713970151158.20683.30695.441.7813080133391.98683.50695.391.7414000146994.99636.30645.591.4612220124531.91
5 结论
本文提出一种基于波面分解的跨海桥梁下部结构波浪荷载计算方法,分别从波浪理论、水槽试验和数值模拟三个方面对计算方法的有效性和准确性进行了对比验证,得到的主要结论如下。
(1)当波高不大时,本文方法得到的水质点速度和加速度沿水深分布与线性波浪理论值吻合良好;对于非线性规则波,因本文方法未考虑非线性效应,在水面附近较理论值误差较大。
(2)对于水槽试验中波高仪测得的规则、不规则波面,本文方法得到的水质点速度时程、速度谱与水槽试验结果吻合较好。
(3)本文方法基于不规则波面时程得到的圆柱桥墩波浪荷载与数值模拟结果吻合良好,墩底剪力峰值相对误差在3%左右,墩底弯矩峰值相对误差在8%左右。相比数值模拟,本文方法无需结构建模,具有更高的计算效率。同时,当能够根据规范、试验得到合适的水动力系数时,本文方法也适用于矩形桥墩、群桩等桥梁下部结构的波浪荷载计算。
本研究为基于波浪实测进行跨海桥梁下部结构波浪荷载监测提供了一种可行的策略,对建立深水大跨桥梁灾害预警系统具有借鉴价值。但本文方法采用的线性波浪理论在波高较大时存在一定误差。考虑到实际水深、波浪要素的复杂性,对于结构波浪荷载计算问题还需开展进一步深入细致的研究。

