彩色形态学无人机航拍影像边缘检测算法*

秦 娜,苏金凤

(1.西北师范大学 计算机科学与工程学院，甘肃 兰州 730070;2.西北师范大学 数学与统计学院，甘肃 兰州 730070)

0 引言

数学形态学是以形态为基础对图像进行分析的数学工具，它的基本思想是用具有一定形态的结构元素，去度量图像中对应的形状，以达到对图像分析和识别的目的[1]。SERRA J[2]、STERNBERG S R[3]等将二值形态学推广到对灰度图像处理，对结构单元内像素按照灰度值排序，并寻找排序后的最大值和最小值。近年来，针对彩色图像的形态学研究是彩色图像处理的一个重要研究方向[4-6]，然而彩色图像是矢量函数，不能直接比较大小。2006年，EVANS A N和LIU X U[7]采用矢量排序算法，提出了基于数学形态学梯度算子的彩色图像边缘检测算子，新的算子改善了传统形态学算子对噪声较为敏感的缺陷。2013年，雷涛等人[6]对RGB颜色空间的三个分量分别按照灰度形态学方法处理，然后融合得到彩色图像，但是这种方法没有考虑RGB分量间的相关性，而且会引入新的彩色值从而改变原始图像的信息。更多关于矢量顺序的彩色边缘检测方法可参见文献[8-10]。就矢量排序统计理论而言，主要问题在于算法缺乏通用的排序标准而且计算复杂性较高，从而导致基于矢量排序的彩色图像边缘检测方法难以被广泛应用。

无人机航拍影像的边缘集中了图像的很多信息，它的检测对于整个图像的识别与理解是至关重要的[11]。目前，对于无人机航拍影像检测已有大量研究，特别是对城市道路、建筑物的检测[12]。但是，大多数算法都集中在主要目标的检测，对多样化的目标整体检测时效果甚微，缺乏完整性，不利于场景的整体识别和理解。随着无人机航拍影像空间分辨率的提高，对其处理的要求也越来越高，迫切需要开发一种针对无人机航拍影像的边缘检测算法，为后续目标的提取与识别打下基础。

针对以上问题本文提出在RGB颜色空间中采用标准化欧氏距离和夹角余弦相似度来衡量两个彩色矢量之间的相似性程度，并结合人类视觉感知定义彩色矢量互相关性度量函数，以此函数为准则定义结构单元内彩色像素集合的上确界和下确界，构建彩色形态学的基本算子。这种彩色形态学充分考虑了RGB颜色空间中的相互关系以及个人视觉感知存在的差异性，对彩色图像的膨胀、腐蚀操作更加平缓，不会改变原始影像的色彩信息，有利于图像细节特征的保持，最终达到彩色图像分析和处理的目的。将提出的彩色形态学操作进一步应用于无人机航拍影像，通过实验对比验证边缘检测的效果，说明其实用性和有效性。

1 互相关性度量函数的彩色形态学方法

1.1 彩色矢量互相关性度量函数的定义

RGB颜色空间是大部分彩色图像获取与显示设备最常采用的三维矢量模型，一幅n×n大小的彩色图像可以用矢量集合表示：

X={x(i,j,k)|i=1，…，n,j=1，…，n,k=R，G，B}

其中，R、G、B分别表示其中某一彩色矢量的红、绿、蓝分量。

在RGB颜色空间中，给定一对彩色矢量x,x∈X，则其互相关性度量函数定义为：

μ(x,x′)=λ×δds(x,x′)+(1-λ)×cos(θ(x,x′))

(1)

其中，λ和δ∈[0,1]是互相关性度量函数的两个调节参数，ds(x,x′)是两个彩色矢量的标准化欧氏距离，θ(x,x′)是两个彩色矢量的夹角，其分别定义为：

(2)

(3)

由公式(2)计算的标准化欧氏距离主要用来衡量矢量间绝对距离的差异，这是一个数学期望值为0，方差值为1的结果，因为彩色矢量的RGB三分量对色彩值的贡献程度是不同的，即：数据各个维度分量的分布不同。如果直接计算矢量欧氏距离，对彩色矢量间距的衡量将不够准确，所以要先将各分量都标准化到均值、方差相等。公式(2)中SR、SG、SB分别表示R、G、B三分量的标准差，其定义如下：

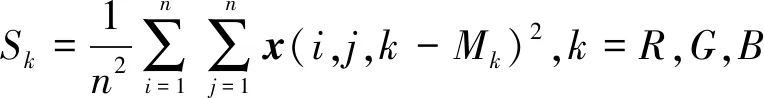
(4)

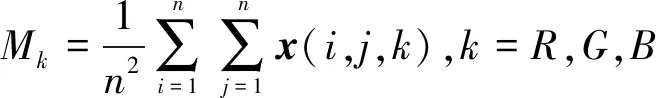
(5)

公式(4)中的Mk表示彩色图像R、G、B三分量的平均值。因为彩色矢量既有大小又有方向，公式(3)计算的是彩色矢量夹角余弦相似度，用来衡量两个彩色矢量方向上的差异。

由(1)式可以看出，定义的彩色矢量互相关性度量函数的取值范围在0与1之间，其表示的含义是，当两个彩色矢量的距离和夹角越接近时，其相似性越大，对应的度量函数值越接近1；反之，当两个彩色矢量的距离和夹角越大，其相似性越低，对应度量函数值越接近0；当两个彩色矢量完全相同时，其距离值与夹角都为0，对应度量函数值等于1，这代表最大的相似性程度。以上定义充分考虑了RGB颜色空间中彩色矢量的相互关系，与生活中彩色影像的采集与显示硬件设备完全吻合。除此之外，人眼视觉系统对色彩的感知由于个体生理、心理和社会认知等方面的巨大差异而存在不同，因此在彩色矢量互相关性度量函数的定义中引入参数λ和δ，这两个参数的取值都在0与1之间，通过对参数调节，可以使彩色矢量互相关性度量函数值更加符合人眼视觉感知的不确定性。这是构建彩色形态学的基本理论基础。

1.2 基于互相关性度量函数的彩色形态学基本算子

由于现有彩色矢量排序方法缺乏明确、统一的标准，通用性较差，将灰度形态学推广到彩色形态学存在很多困难[13-15]。彩色形态学处理的根本是寻求矢量元素的最小值及最大值，只要建立合适的完备格空间，就可以定义彩色形态学算子[16]。为了避免彩色矢量排序的难题，本文在上述定义的基础上提出一种新的彩色形态学方法，以彩色矢量互相关性度量函数为准则定义结构元素内彩色矢量集合的上确界和下确界，并构建彩色形态学的基本算子。

给定一幅n×n大小的彩色图像，其中所有彩色矢量构成集合：

X={x(i,j,k)|i=1，…，n,j=1，…，n,k=R，G，B}

设结构元素为大小的彩色矢量集合：

Y={y(i,j,k)|i=1，…，n,j=1，…，n,k=R，G，B}

其中，Y是X的非空真子集。

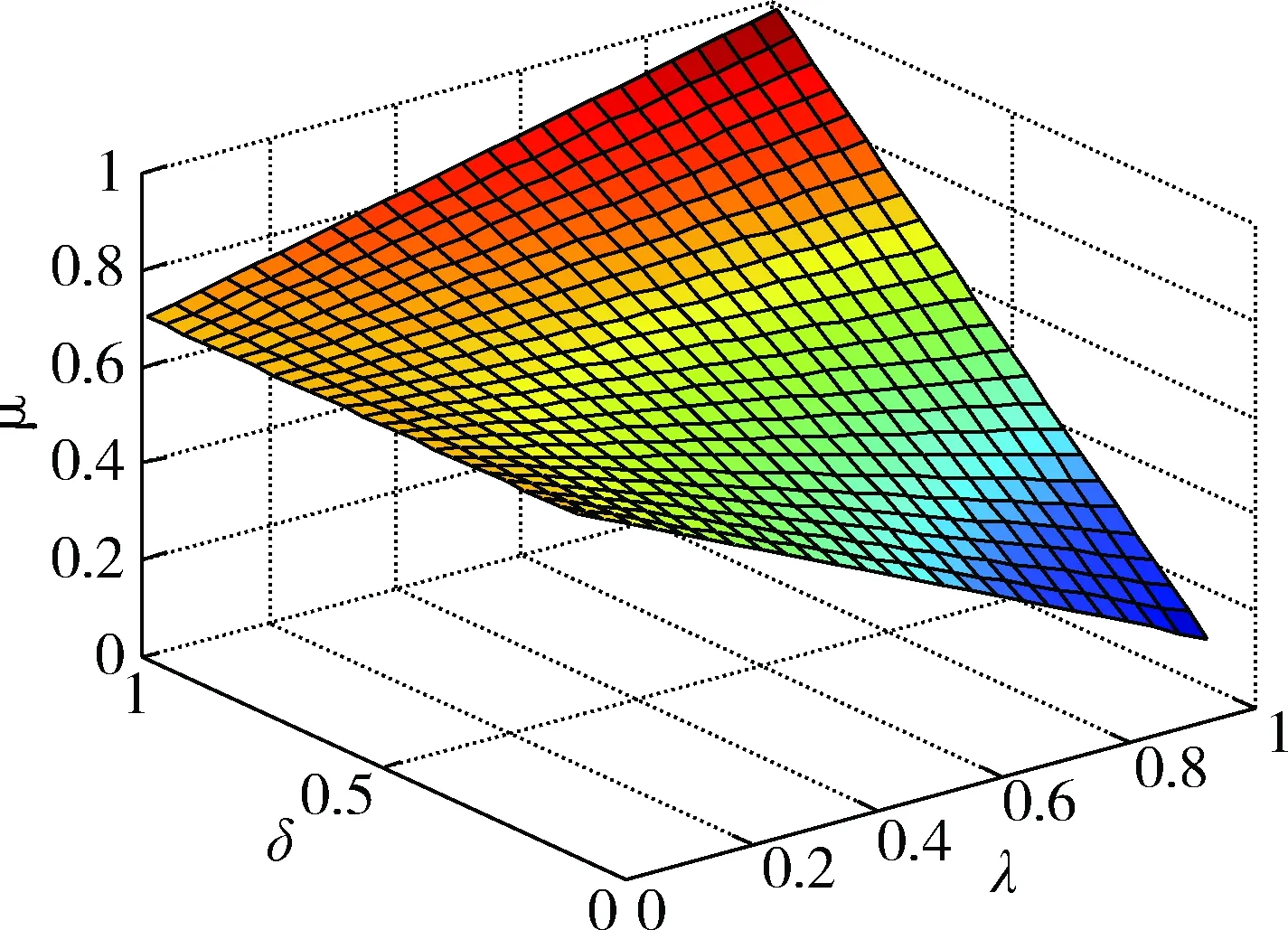
在结构元素集合Y中，根据公式(1)计算每个彩色矢量y(i,j,k)与Y中所有矢量的互相关性度量函数值，计算的结果得到一个(m×m)2大小的矩阵A，该矩阵主对角线上的元素全部为1，其他元素按照主对角线对称。当结构元素集合Y的参数取值m=5，互相关性度量函数的调节参数取值λ=0.5,δ=0.5时，计算出矩阵A，其互相关性度量函数的变化情况如图1所示。

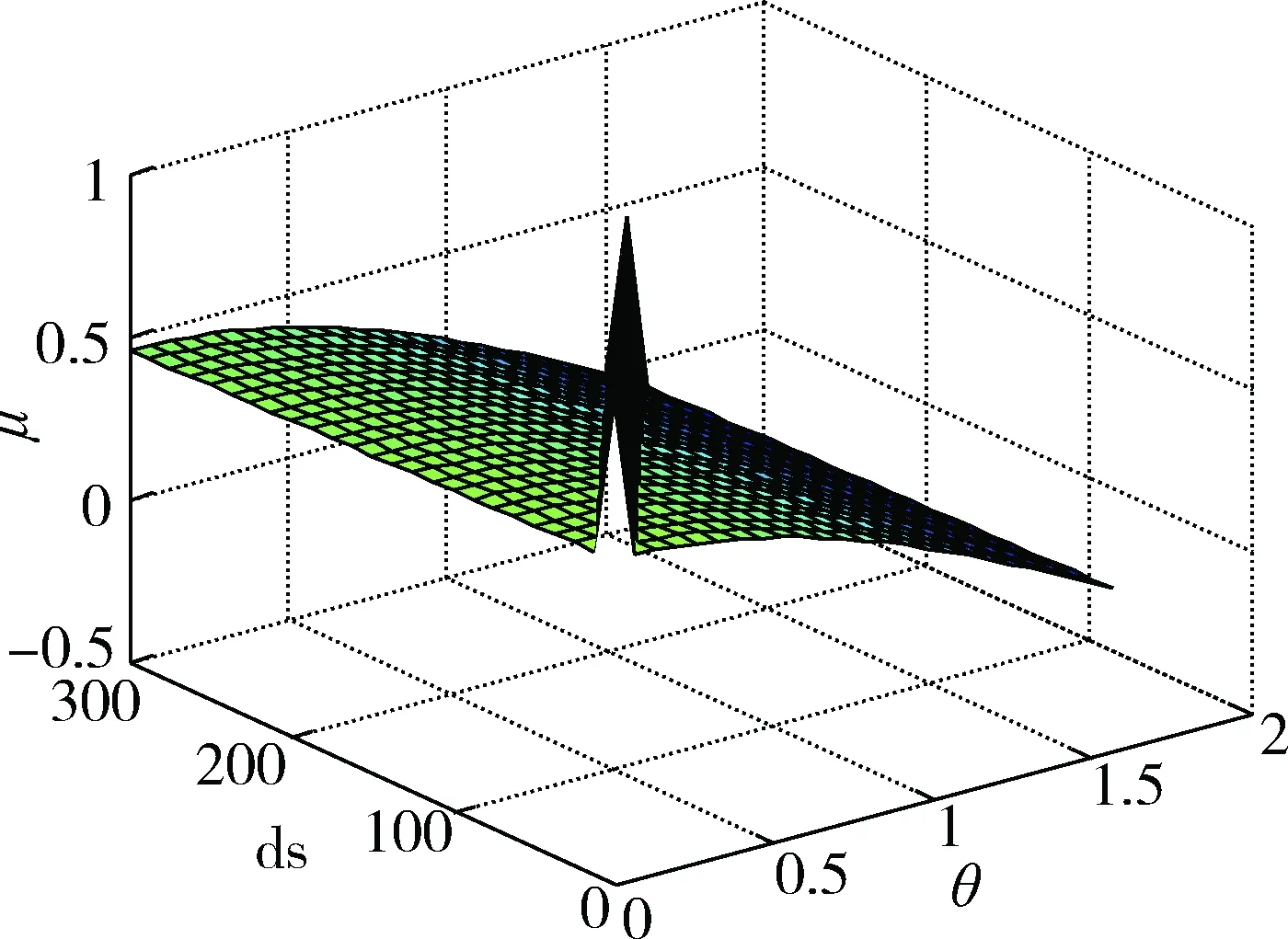
图1 λ=0.5，δ=0.5时，互相关性度量函数变化情况

根据公式(1)分析可知，矩阵A的元素取值在0与1之间。现计算矩阵A中元素的最小值，得到Y中最不相似的两个彩色矢量，即：找到结构元素Y中求得互相关性度量函数最小值所对应的一对彩色矢量，将其分别记为y1和y2。

μ(y1,y2)=min(min(A))

以此为依据，定义结构元素集合Y的上确界∨和下确界∧如下：

(6)

(7)

由公式(6)和(7)可以看出，∨Y和∧Y操作输出的彩色矢量分别是结构元素内最不相似的一对矢量y1和y2，其中模值较大的彩色矢量定义为上确界操作，模值较小的矢量定义为下确界操作。这样的输出结果计算方法简单，运算效率高，并且不会产生新的颜色矢量，有效保存了集合X的原始信息。本文提出的彩色形态学方法就是以上述∨Y和∧Y操作为基本准则，定义膨胀算子、腐蚀算子、开运算和闭运算等基本形态学操作。

用结构元素Y对输入彩色图像X进行膨胀记为X⊕Y，其定义为：

X⊕Y(s,t,k)=∨{X(s-x,t-y,k)+Y(x,y,k)|((s-x),(t-y),k)∈DX,(x,y,k)∈DY,k=R,G,B}

(8)

式中，DX和DY分别是X和Y的定义域，k代表彩色矢量的R、G、B三分量。

用结构元素Y对输入彩色图像X进行腐蚀记为X⊗Y，其定义为：

X⊗Y(s,t,k)=∧{X(s+x,t+y,k)+Y(x,y,k)|((s+x),(t+y),k)∈DX,(x,y,k)∈DY,k=R,G,B}

(9)

彩色形态学中关于开启和闭合的表达与它们在二值数学形态学中的对应运算是一致的[1]。

用结构元素Y开启彩色图像X的操作记为X∘Y，其定义为：

X°Y=(X⊗Y)⊕Y

(10)

用Y闭合X记为X·Y，其定义为：

X·Y=(X⊕Y)⊗Y

(11)

1.3 互相关性度量函数的参数分析

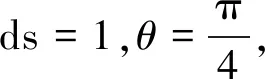
图时对互相关性度量函数的影响

为了研究单个参数对互相关性度量函数的影响，令公式(1)中δ=0.5，当λ分别为0、0.1、0.3、0.7时，μ值的变化情况如图3所示。图3(a)中由于λ=0，μ值仅与夹角θ有关而与标准化距离ds无关，当夹角θ为0时互相关性度量函数取得最大值1，μ值随着彩色矢量夹角θ的增大逐渐减小。如图3(b)～图3(d)所示，当λ取值逐渐增大时μ值迅速减小，说明互相关性度量函数对参数λ的变化比较敏感；还可以看出，随着λ增大图中突起部分的变化更加剧烈，这是由于参数λ可以用于调节矢量间距离与夹角的权重，其重要性越大则互相关性度量函数值越大。

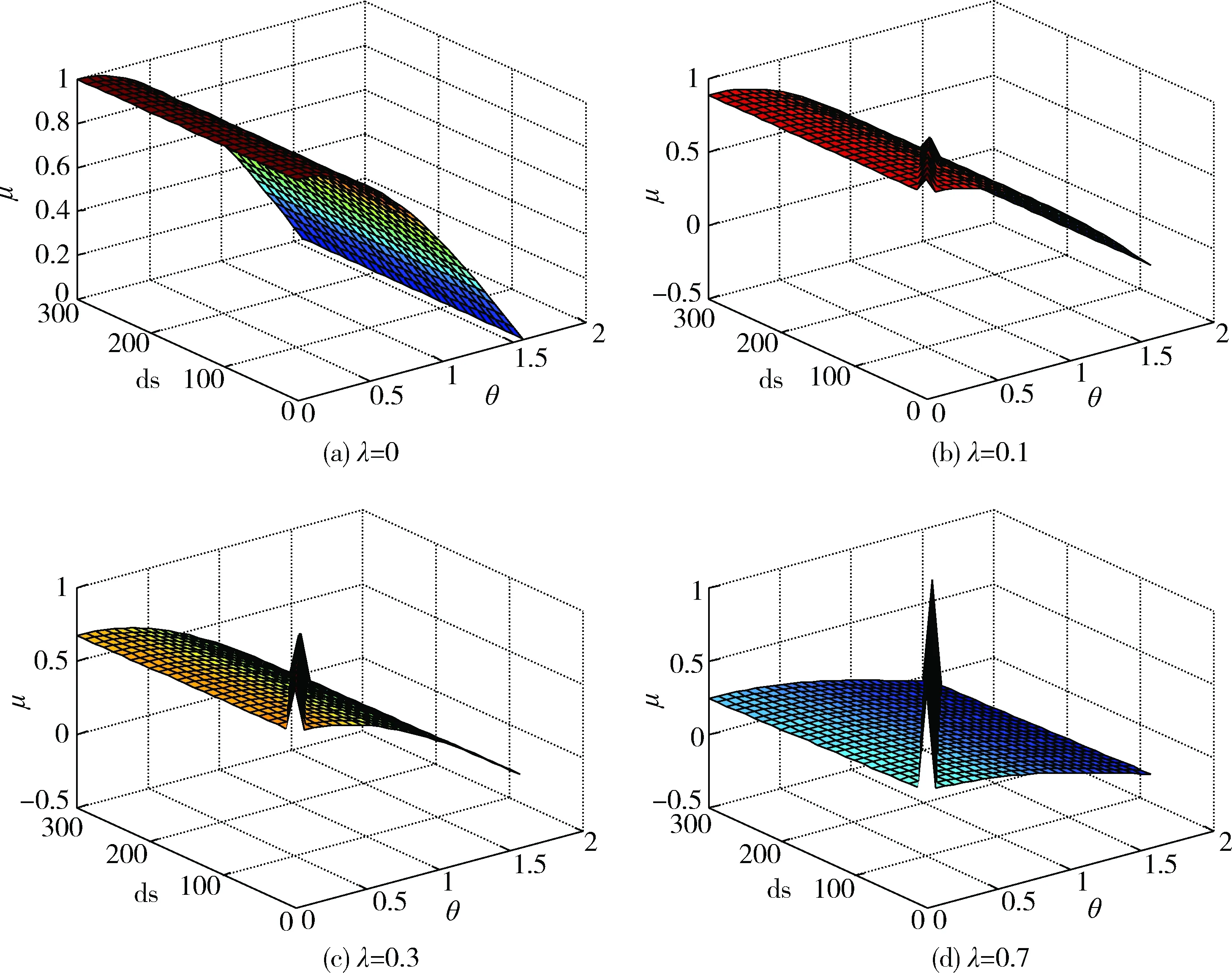
图3 δ=0.5，λ分别为0、0.1、0.3、0.7时互相关性度量函数

同理，为了说明参数δ对互相关性度量函数的影响，根据公式(1)假设λ=0.5,ds=1，当参数δ在开区间(0,1)中变化，并结合两个彩色矢量夹角θ改变时，互相关性度量函数值μ的变化情况如图4所示。从图中可以看出，μ值随着参数δ增大而逐渐增大，随着夹角θ增大而逐渐减小。说明可以通过调节参数δ的取值改变度量函数的结果，这符合彩色矢量相似性判断因人而异的特点，使互相关性度量函数更加符合人眼视觉感知的不确定性。

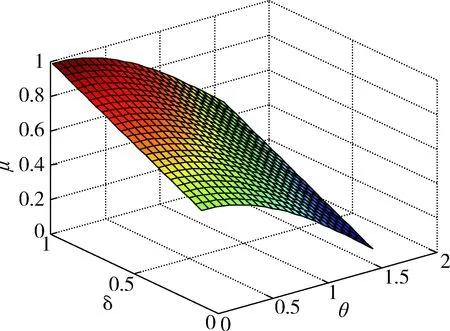
图4 λ=0.5,ds=1互相关性度量函数变化情况

2 彩色形态学操作实验

为了验证本文提出的彩色形态学方法，选择一幅无人机拍摄的高空遥感影像如图5(a)所示，该彩色图像尺度大小为200×200×3，图像中包括红色的车辆、绿色的草地以及蓝色的房顶等丰富的彩色信息，也包括房顶边缘、草坪与树木的纹理等细节信息。

图5 彩色形态学实验

2.1 彩色形态学基本操作实验结果与分析

现将本文提出的彩色形态学操作应用于该图像，其中结构元素尺度大小为3×3，调节参数取值λ=0.5,δ=0.5。实验结果如图5(b)～5(e)所示。

膨胀算子具有放大功能，由图5(b)可以看出草坪的白色边界变粗，而高楼左侧的树荫形状变小，说明图像中比背景亮的部分得到扩张，而比背景暗的部分得到收缩。反之，腐蚀算子具有收缩功能，由图5(c)可以看出草坪的白色边界变细，而图像中比背景暗的部分面积扩大了，图像中的小细节被去除，同时目标颜色及边缘变得更加平滑。如图5(d)所示，开运算消除了比结构元素尺寸小的亮细节，而保持图像色彩和亮度基本不受影响。这是因为开运算首先用腐蚀算子去除了小的亮细节，同时使图像亮度减弱，接着用膨胀算子增加并恢复图像亮度，但不会重新引入前面去除的细节。闭运算与开运算的结果相反，如图5(e)所示，闭运算在消除图像中较小暗细节的同时保持图像色彩和暗区域基本不受影响。因此，开运算和闭运算都可以抑制比结构元素小的特定图像细节，同时保证不产生全局的几何失真。

2.2 彩色形态学对比实验与分析

为了将本文提出的彩色形态学操作与现有算法进行对比，仍然以图5(a)作为实验图像，结构元素取3×3大小。对RGB颜色空间的三个分量分别按照灰度形态学处理后融合为彩色图像的方法，称为M序算法；基于多元数据排序准则的彩色形态学，称为C序算法。为了说明形态学算子的处理过程，选择图5(a)中某一3×3×3大小的矢量集合进行实验，其三分量取值如表1所示。

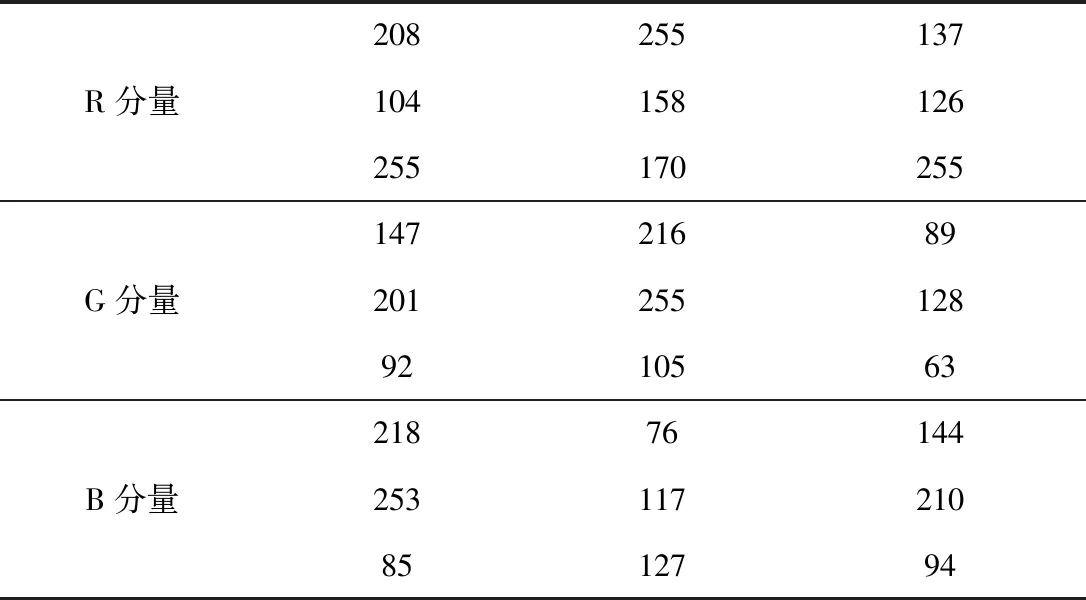
表1 R、G、B分量取值

该矢量集合的中心像素为(158,255,117)，分别采用M序算法、C序算法和本文算法计算膨胀算子和腐蚀算子，计算结果如表2所示。

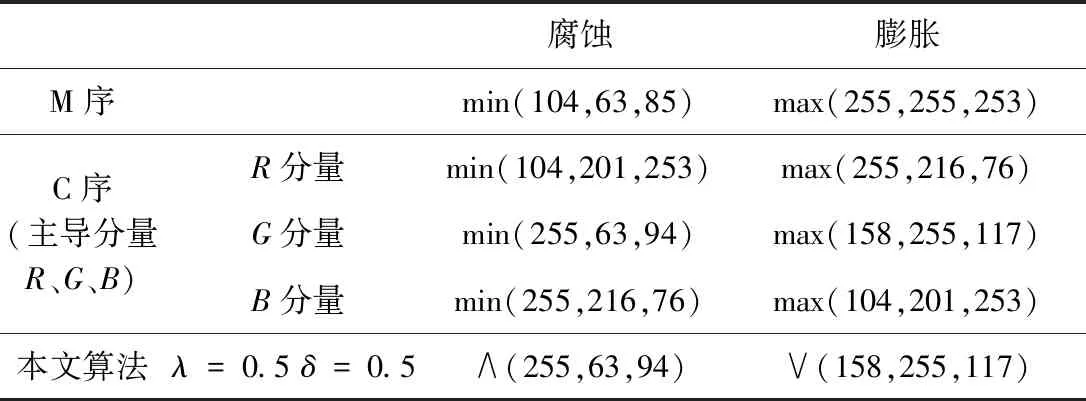
表2 不同算法膨胀算子和腐蚀算子计算结果

可以看出M序算法没有考虑三个通道之间的相关性，得到的最小值及最大值在原矢量集合中并不存在，新色彩的引入破坏了原始彩色图像的拓扑结构。而C序算法中三个分量比较次序是人为规定的，实验中分别以R、G、B为主导分量进行排序，计算结果相差很大，尤其在本例中，R分量主导排序的最小矢量值与B分量主导排序的最大矢量值结果相同，因此算子性能较差。而本文算法基于彩色矢量互相关性度量函数定义算子，采用标准化欧氏距离和夹角余弦相似度作为明确的标准，同时结合人眼视觉感知引入控制参数，通过参数分析可以得到高性能彩色形态学算子，并适用于无人机航拍影像的建筑物检测。

通过以上实验分析表明，本文提出的彩色形态学操作符合数学形态学的基本原理，对彩色图像膨胀和腐蚀操作更加平缓，有利于图像细节特征的保持，并且不会引入新的彩色矢量而改变原始图像的色彩信息。本文提出的彩色形态学方法可以应用于背景估计和消除、边缘的形态检测、图像快速分割、纹理分割等方面，最终达到有效分析处理彩色图像的目的。

3 基于彩色形态学的无人机航拍影像边缘检测算法

一般边缘检测算法得到的都是边缘点，这仅仅反映图像的局部信息，为了实现无人机航拍影像显著特征的提取与识别，首要任务是获得完备的边缘信息。

3.1 彩色形态学边缘检测算子

许多常用的边缘检测算子，其检测原理是通过计算图像的局部微分得到灰度剧烈变化的像素点，但这些算子对噪声较敏感并且会增强噪声。图像的形态学梯度是局部边缘重要性的一个测度，基于形态学的边缘检测方法虽然也对噪声敏感但是不会加强或者放大噪声，而且彩色形态学边缘检测算子操作的结果仍然是RGB空间的彩色图像。因此，首先采用本文提出的彩色形态学方法对无人机航拍影像进行处理，计算图像的彩色形态学梯度得到边缘特征。依据本文公式(8)与公式(9)，设X与Y分别代表彩色图像和结构元素，基本的彩色形态学梯度定义如下：

grad1=(X⊕Y)-(X⊗Y)

(12)

X⊕Y将原始彩色图像中的亮区域扩展一个像素的宽度，而X⊗Y又将该亮区域收缩一个像素的宽度，所以grad1计算的边界宽度为两个像素。如果想要获得单像素边界，可用如下公式定义形态学梯度：

grad2=(X⊕Y)-X

(13)

grad3=X-(X⊗Y)

(14)

公式(13)和(14)的区别是公式(13)计算的单像素边缘实际上是在图像背景中，而公式(14)计算得到的单像素边缘会属于目标。

上述形态学梯度的定义方法都不会放大图像中的噪声，但是仍然保留了原来的噪声。为了减少随机噪声对建筑物提取的影响，本文采用如公式(15)的方式定义形态学梯度，使其对图像中的孤立噪声不敏感，适用于无人机高分辨率影像的边缘检测。

grad4=min{[(X⊕Y)-X],[X-(X⊗Y)]}

(15)

3.2 实验结果与分析

为了验证本文提出的彩色形态学梯度算子，仿真实验选用图6的无人机航拍影像作为实验图像。

图6 无人机航拍影像

为了说明本文算法的优越性，利用不同的方法对无人机航拍影像进行边缘检测，结果如图7所示。图7(a)～图7(c)是采用经典边缘算子。图7(d)～7(f)是利用本文算法的公式(13)～公式(15)定义的彩色形态学方法得到的检测结果。

图7 不同方法对无人机航拍影像的边缘检测结果对比

从实验结果来看，本文提出的彩色形态学方法能检测到更多的图像细节，效果最好。边缘函数的检测算法中Roberts算子明显只能检测到很少的边缘；Prewitt算子虽然能检测到图像边缘，但是对细节边缘存在漏检；Sobel算子得到的图像有更多的图像边缘，但是明显有较多的伪边缘信息。利用彩色形态学方法的公式(13)得到的图像有完整连接的边缘信息，更加凸显很多边缘细节；利用公式(14)所得的图像清楚地表示了建筑物的轮廓信息，易于观察和辨识；利用公式(15)所得的图像虽然亮度变暗，但是有完整的建筑物边缘信息。因此，本文方法能够完整检测到连接的建筑物边缘信息，有助于建筑物的进一步提取。

为了说明本文提出算法的有效性和实用性，利用图5(a)加入参数为0.01的椒盐噪声得到图8(a)的噪声原图，再通过经典边缘算子检测，进行对比实验，得到图8(b)～图8(d)，图8(e)是利用公式(15)得到的边缘检测结果。

不难发现，公式(15)的效果明显优于经典边缘算子的检测结果。观察图8(b)～图8(e)，比较各种方法的结果，由图8(b)～图8(d)可知，经典边缘算子产生的边缘不清晰，边缘定位模糊，特别是对含有复杂结构的建筑物(如图8(b)左侧建筑物、图8(c)右侧建筑物、图8(c)左右两侧建筑物)会产生较明显的污染，并且有细节丢失；而采用公式(15)的图8(e)虽然亮度较暗，但是能清楚地看到建筑物的边缘，说明边缘定位准确，且保留更丰富的细节(如左右两侧建筑物)，在低对比度的非边缘处基本没有污染现象，更好地有助于建筑物的提取和识别。

4 结束语

本文基于彩色矢量互相关性度量函数的定义提出彩色形态学方法。为了避免矢量排序的难题，本文在给定结构元素的作用下以该函数为准则定义矢量集合的上确界和下确界，实验验证该算子效果良好。进一步将该算子应用于无人机航拍影像边缘检测，通过参数调节能够应对不同需求的提取工作，同时也证明了本文彩色形态学方法的实用性和有效性。如何将该方法推广到视频处理和医学图像检测中是我们今后的研究方向。