基于LFSR的前馈模型在量子随机数提取器中的应用*

杨晓亮，刘翼鹏，黄严严

(1.信息工程大学，河南 郑州 450001；2.61497部队，北京 100089)

0 引言

真随机数是指随机数的信息熵达到最大，具有不可预测、相互独立、分布均匀和不可重复等性质，被广泛应用于数值模拟、抽样统计、算法设计等研究领域，特别是在保密通信中，发挥着至关重要的作用。而现实中，由于噪声源的信息泄露，攻击者可能获取初始随机数源的部分信息，所以生成的初始随机源往往是弱随机源，即随机数的信息熵达不到最大。通过随机数提取器从弱随机数源中提取真随机数是获得真随机数常用的方法之一[1]。

基于是否需要额外真随机种子的加入，随机数提取器分为有种提取器和无种提取器两大类。有种提取器虽然需要额外随机种子的输入，但其对初始弱随机数源的要求较低，因此目前使用更多的是有种提取器。Trevisan结构的随机数提取器就是典型的有种提取器，其构造方法是将额外真随机种子以一定的规则进行分组，该分组方法被称为“弱设计”，将经“弱设计”处理后的种子与初始弱随机数源输入到一比特随机数提取器中，然后通过级联多个一比特随机数提取器的输出，从而获得一串真随机序列。Trevisan结构的随机数提取器具有所需的随机种子较短、抗量子攻击、种子可以重复利用(强随机数提取器)三大优势，故受到广泛关注和应用。

随机种子使用量和实现效率是衡量一个有种提取器性能的两个重要指标。在实践中，随机种子仍然是极为稀有的资源，尽管弱设计环节一定程度上缩短了种子的长度，然而其使用量仍然很大，并且存在种子的重用问题，为此文献[1]利用输出反馈模式结合简化的DES算法对随机种子进行伪随机扩展，当弱随机数源的输入长度为n时，在理想情况下(反馈序列周期达到最大)能将真随机种子的使用量由原来的O(log3n)减少到O(logn)，在种子集合之间的相关性较小的条件下，避免了种子的重用问题。但这种方法存在两个不足，其一是只有在理想情况下才能将真随机种子减少到O(logn)，其二实现效率可待进一步提高。

线性反馈移存器(LFSR)是序列密码设计中常用的一种初始乱源，其目的是以种子密钥为反馈移存器的初态，按照确定的递推关系，产生一个周期长、统计特性好的初始乱源，从而为进一步利用非线性变换等设计手段，产生抗破译能力强的乱数序列提供“原料”[2]。考虑到LFSR具有结构简单、运算速度快、生成的序列周期长、统计特性好等优点，本文使用基于LFSR的前馈模型扩展随机种子，并结合一比特随机数提取器——Xor-code，给出了此类短种子随机数提取器模型在量子边信息下的安全性分析及具体实现参数，并与基于Trevisan结构及输出反馈模式的随机数提取器进行了对比分析，发现利用广义LFSR的前馈模型也可以将真随机种子的使用量缩小为O(logn)，且实现效率较高。

1 相关知识

本节首先介绍基于Trevisan结构的随机数提取器模型，然后介绍线性反馈移存器。

1.1 基于Trevisan结构的随机数提取器模型

2001年，TREVISAN L利用Nisan-Wigderson[3]伪随机数生成器和一类纠错编码list-decodable codes构造一比特输出的随机数提取器[2]。TREVISAN L证明了在初始弱随机数源的最小熵足够大的情况下，将其进行编码后，利用随机种子随机的挑选此类纠错编码一个输出位置的比特，则该比特是接近真随机的。

同时，TREVISAN L利用该一比特输出的随机数提取器，构造一类多比特输出的随机数提取器，并证明了在初始弱随机数源最小熵满足一定条件的情况下，将一比特随机数提取器的输出级联所产生的多比特输出是接近真随机的。TREVISAN L在构造多比特随机数提取器时，为了使用更少的种子，利用了NISAN N和WIGDERSON A提出的交集结构[3]，之后并经RAN R等人[4]的改进，拥有较好的性质，这类方法被统称为“弱设计”。

定义1[4]一个集合族S1,…,Sm⊂[d]，如果满足

(1)对于所有的i，|Si|=t。

其中r定义为种子“弱设计”的重叠度，则称S1,…,Sm为一个(t,r) “弱设计”。

Trevisan结构的随机数提取器模型可以描述为定义2。

定义2[2]对于一个一比特随机数提取器C:{0,1}n×{0,1}t→{0,1}，其种子长度为t，以及一个(t,r) “弱设计”，定义m比特随机数提取器ExtC:{0,1}n×{0,1}d→{0,1}m为

ExtC(x,y)=C(x,yS1),…,C(x,ySm)

(1)

其中ySi为序列y中由Si集合确定的那些位置的比特。

对初始种子进行“弱设计”，在一定程度上缩短了种子的长度，但其种子使用量依旧很大，且存在种子的重用问题。针对这些问题文献[1]利用输出反馈模式结合简化的DES算法对随机种子进行伪随机扩展，取得了良好的效果。对于输出反馈模式的随机数提取器模型及其量子边信息下安全分析证明的介绍可参考文献[1]。

1.2 线性反馈移存器

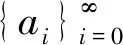
am=f(am-1,am-2,…,am-n)

(2)

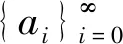
am=c1am-1+c2mm-2+…+cnam-n

(3)

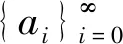
对n位寄存器增加移位功能就是n级移位寄存器，带反馈电路的寄存器就是反馈移位寄存器，简称反馈移存器。n级反馈移位寄存器就是实现变换

(4)

的一个数字逻辑电路。当反馈移存器的反馈函数f是线性函数时，即:

f(x1,x2,…,xn)=c1x1+c2x2+…+cnxn

(5)

则称该反馈移存器为线性反馈移存器(LFSR)。

LFSR的初始设定值称作种子，由n级递归序列的定义可知其能达到的最大周期为2n，故n级LFSR其状态序列至多是2n。而LFSR产生大于1的状态序列不可能出现全0状态，因此最多能够产生2n-1位长不可重复的伪随机序列。

n级LFSR所能产生最大周期长为2n-1的序列称为m序列。当LFSR的反馈多项式是本原多项式时，便可保证其产生的序列是m序列。m序列的伪随机性能满足Golomb的3个随机性假设，即平衡特性、游程特性、自相关特性。故在实际应用中，通常使用反馈多项式为本原多项式的LFSR。所以，LFSR产生的伪随机数具有很好的随机性。此节内容可见文献[5]。

2 基于LFSR的前馈模型的随机数提取器及在量子边信息下安全性分析

2.1 LFSR的前馈模型扩展随机数种子

由于LFSR按线性方式生成的输出序列具有线性制约性，故不能直接作为伪随机序列使用。利用非线性变换对反馈移存器的输出或者状态序列进行进一步加工，达到破坏其线性制约性，并保持m序列的周期长和统计特性好的优点[5]。

前馈模型主要由LFSR和非线性变换g(x)组成，其逻辑框图如图1所示。

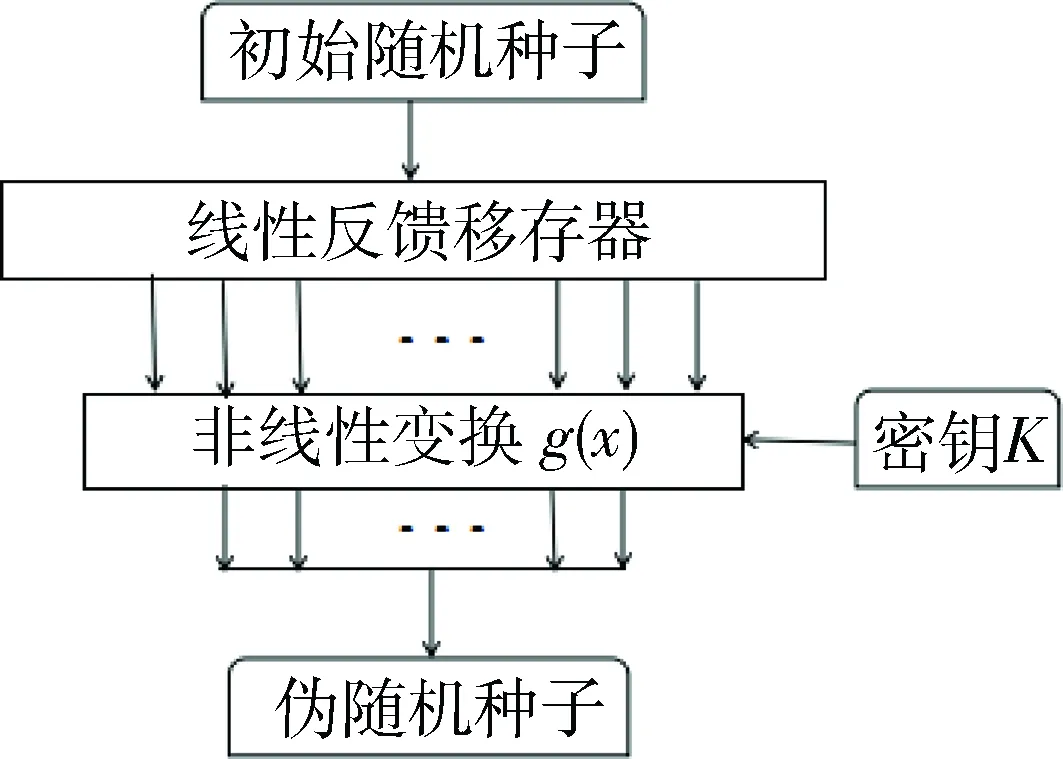
图1 基于线性反馈移存器的前馈模型

其中非线性变换g(x)受密钥控制时，密钥K的长度为O(1)；非线性变换g(x)也可能不受密钥控制，此时密钥K的长度为0。设随机数提取器输出长度为m，具体种子扩展过程如下：

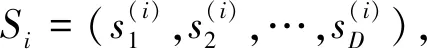
(6)

(2)将得到的2D-1比特的伪随机序列d1,d2,…,d2D-1分为t比特每组，记为y1,y2,…,ym，再分别作为种子输入一比特随机数提取器。

由于LFSR是序列密码设计中常用的一种初始乱源，在实际应用中，大部分序列密码算法都可应用到该模型中，以扩展随机种子。

2.2 结合Xor-code构造短种子随机数提取器

考虑到实现速度，使用Xor-code[6]来进行一比特提取，此一比特随机数提取器通过计算输入序列的l个随机位置的异或值，从而得到一比特的真随机数。此结构的计算效率较高，有如下定理。

定理1[7]对于任意的ε>0，n∈N，函数

Cn,ε,l:{0,1}n×[n]l→{0,1}

(7)

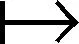
为经典边信息下的(k,ε)强提取器，其中k=h(ln2/l·log2/ε)n+3log1/ε+log4/3，h(p)=-plogp-(1-p)log(1-p)为二元熵函数，种子长度t=llogn。

结合LFSR的前馈模型随机种子扩展算法及一比特随机数提取器Xor-code，可得短种子随机数提取器如定义4。

定义4对于一比特Xor-code随机数提取器C:{0,1}n×{0,1}t→{0,1}，其种子长度为t，以及经LFSR的前馈模型伪随机扩展后的种子集合y1,…,ym，定义m比特随机数提取器ExtC:{0,1}n×{0,1}d→{0,1}m为

ExtC(x,y):=C(x,y1)…C(x,ym)

(8)

2.3 基于前馈模型的随机数提取器在量子边信息下的安全性分析

引用文献[1]中短种子随机数提取器模型在量子边信息下的安全性分析证明结果，很容易得到如下定理。

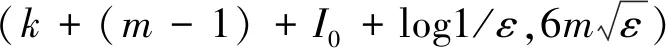
3 具体实现参数及与Trevisan结构、输出反馈式模型的对比分析

由MAUERER W等人[7]的研究可知，使用Xor-code作为一比特随机数提取器时，其所需种子长度约为t=llogn=O(logn)比特。

对于一般的Trevisan结构，其真随机种子的使用量约为[8]

d=O(t2logm)≈O(log3n)

(9)

利用输出反馈式并结合简化的DES算法，在理想情况下，仅需要预制t=O(logn)比特真随机种子，DES算法算法密钥长度为K≈O(logn)，所以

d=D+K=O(logn)

(10)

利用基于LFSR的前馈模型扩展随机数种子，将D比特随机种子作为LFSR的初始状态，生成长度为2D-1比特的m序列，再经非线性变换g(x)打破其线性制约，得到2D-1比特伪随机序列。由于使用Xor-code作为一比特随机数提取器，其种子长度约为t=O(logn)比特，故定义4给出的m比特随机数提取器所需的伪随机序列长度为t=O(mlogn)=O(nlogn)比特，所以有

2D-1=O(nlogn)

(11)

即可得所需的随机种子量为D=O(logn)。又因为K=O(1)，故

d=D+K=O(logn)

(12)

经上述分析可知，本文提出的基于LFSR的前馈模型，相比Trevisan结构，解决了存在比特重用问题，且缩小了初始随机种子的使用量。在理想情况下，输出反馈式的随机数提取器可将种子使用量降低到O(logn)，而本文提出的提取器模型，在满足模型要求的任何情况下都能将随机种子使用量降低到O(logn)。且序列密码的实现效率远远高于分组密码，故基于LFSR的前馈模型的提取器实现效率较高。

4 结论

本文利用LFSR的前馈模型扩展随机种子，不仅解决了基于Trevisan结构的随机数提取器模型随机种子使用量较大、存在比特重用等问题，而且实现效率较输出反馈式随机数提取器更高。结合一比特提取器Xor-code，将提取器结构模块化，设计了一类量子边信息下强随机数提取器。给出了实现的具体参数及与Trevisan结构、输出反馈式随机数提取器进行对比分析，结果表明，本文的提取器结构在缩小随机种子使用量上有良好的效果，且实现效率较高。