SKINNY-n-n算法和MANTIS算法的相关密钥分析*

石淑英，何 骏

(郑州信大捷安移动信息安全关键技术国家地方联合工程实验室，河南 郑州 450004)

0 引言

SKINNY算法族是由BEIERLE C等人[1]在CRYPTO 2016上提出的一个可调轻量级分组密码算法族，主要目的是为了设计出一种软硬件实现都非常高效，并且性能能够比NSA提出的候选算法SIMON更好的轻量级分组密码算法。此外，设计者也提出了SKINNY算法的一种低延迟的变体MANTIS算法，与SPECK算法进行性能对比，安全性分析结果对比情况见表1。

SKINNY算法采用的是SPN结构，根据分组规模和密钥规模的不同，表示为SKINNY-n-k，具体可分为SKINNY-n-n、SKINNY-n-2n和SKINNY-n-3n三大类，其中n表示分组规模，k表示可调规模。设计者证明了该算法族对已知的分组密码攻击方法例如差分/线性分析、不可能差分分析、相关密钥分析等有较强的安全性。

MANTIS算法基于PRINCE算法进行改进，即该算法基本结构与PRINCE类似，均采用FX结构[2-3]。轮函数的具体环节中采用的与Midori算法相同的S盒变换、P盒置换以及列混合变换，只是分组状态的排列与Midori算法有所不同，在密钥调度环节采用的是可调模型，设计者认为该步骤能有效提高算法安全性。在算法实现方面，其具有低延迟和易于硬件实现的优点。

TOLBA M等人[4]利用不可能差分技术分析了SKINNY算法在单密钥条件下的安全性，分别对SKINNY-n-n、SKINNY-n-2n、SKINNY-n-3n攻击至18轮、20轮、22轮；LIU G等人[5]给出了算法在相关密钥不可能差分攻击和相关密钥矩阵攻击下的攻击结果，对SKINNY算法族的三大类分别攻击至19轮、23轮、27轮；ANKELE R等人[6]同样采用相关密钥不可能差分技术对SKINNY-64-128算法进行了分析，攻击到了21轮，并且在已知一定数量的密钥的假设条件下，将攻击轮数拓展到了23轮；SADEGHI S[7]等人分析给出了算法在相关密钥不可能差分和零相关线性分析下的攻击路径；DOBRAUNIG C[8]等人给出了针对MANTIS5的实际密钥恢复攻击。现有分析对SKINNY-n-n算法的最好攻击结果仅达到了19轮，对MANTIS算法除MANTIS5外还未有其他的攻击结果。

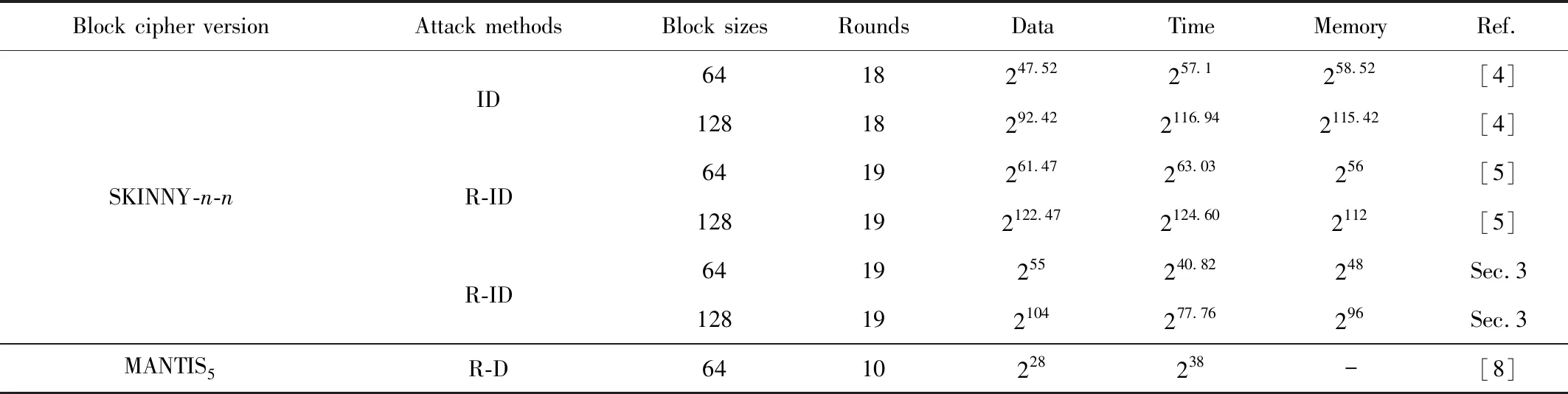
表1 SKINNY与MANTIS算法安全性分析结果对比

注：ID表示不可能差分分析；R-ID表示相关密钥不可能差分分析；R-R表示相关密钥矩阵攻击；R-D表示相关密钥差分分析。

本文中，针对SKINNY-n-n算法，首先通过分析算法的结构特性，给出了两类长度为13轮的相关密钥不可能差分区分器，而后据其中的一种区分器，对算法进行了19轮的相关密钥不可能差分分析。针对MANTIS算法，同样通过分析算法结构特性，并利用相关密钥分析方法，给出了可用于MANTIS算法安全性分析的几类高概率相关密钥区分器。

在第1节中，介绍了SKINNY算法和MANTIS算法的基本结构；在第2节中，首先介绍了SKINNY-n-n算法的相关特性，基于这些性质，给出了两类13轮的相关密钥不可能差分区分器；在第3节中，运用第2节中得到的区分器中的一种，给出了19轮的SKINNY-n-n算法的相关密钥不可能差分攻击结果，并分析了攻击所需的复杂度；在第4节中，首先分析了MANTIS算法的性质，而后据此，给出了几类MANTIS算法的相关密钥区分器。

1 算法介绍

本节中，主要介绍SKINNY算法和MANTIS算法的具体结构，并对文中所用到的具体符号进行解释说明。

1.1 符号说明

SKINNY算法：

ΔXr:第r轮S盒变换前的差分状态，也是第r-1轮列混合变换后的差分状态；

ΔYr:第r轮S盒变换后的差分状态；

ΔZr:第r轮密钥加和常数加变换后的差分状态；

ΔWr:第r轮行移位操作后的差分状态。

MANTIS算法：

ΔX:明文差分与白化密钥异或后的初始差分状态；

ΔX*:密文差分与白化密钥异或后的差分状态；

ΔXSBr，ΔXMCr-1:第r轮S盒变换后的差分状态，也是第r-1轮列混合变换后的差分状态；

ΔXKAr:第r轮密钥加和常数加变换后的差分状态；

ΔXPTr:第r轮P盒置换后的差分状态。

1.2 SKINNY算法

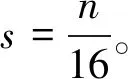
当分组规模为64 bit时，矩阵中的每一比特块表示一个半字节，即s=4；分组规模为128 bit时，每一比特块表示一个字节，即s=8。具体的表示形式如下所示。

SKINNY算法的设计沿用TWEAKEY算法中的设计思想，即其采用可调的密钥输入来替代单纯的密钥和一对可调密钥。该算法根据分组规模n的不同，给出了三种不同的密钥规模，即t=n，t=2n，t=3n。

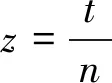
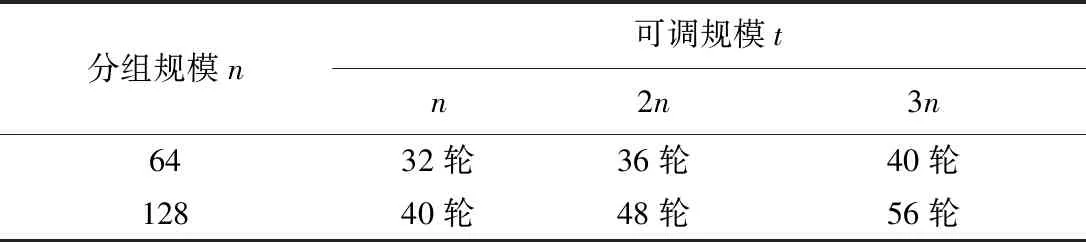
表2 SKINNY算法分组、可调和轮数的对应关系

算法的轮函数包括Subcells、AddConStants、AddRoundTweakey、ShiftRows、MixColumns这五个变换操作，下面将进行具体介绍。此外，本文中主要介绍SKINNY-n-n算法，对其余规模的SKINNY算法不再做具体描述。

S盒变换(Subcells) S盒变换是对输入状态的每一比特块均进行操作，根据分组规模不同，其变换所用的S盒也不同。在这里，仅给出了4-bit S盒S4的具体表示，如表3所示，8-bit S盒S8的具体表示详见文献[1]。

表3 4-bit S盒S4

轮常数加(AddConStants) 通过一个6 bit的随机数发生器生成轮常数，并将其赋值到一个4×4矩阵第一列的前三个比特块，而后将初始状态的第一列的前三个比特块与之进行异或。

轮密钥加(AddRoundTweakey) 实现轮密钥的前两列的值和相对应位置的输入状态的值进行异或，轮密钥由下面介绍的密钥扩展算法生成，对于SKINNY-n-n算法，其轮密钥为TKi=TK1i。

行移位(ShiftRows) 该步骤实现初始状态第0行位置不改变，第1、2、3行分别循环右移1、2、3位，其逆运算SR-1也显而易见。具体表示形式如下：

列混合(MixColumns) 使得初始状态每一列与列混合矩阵做矩阵的乘法运算，达到混乱和扩散的目的。下面给出列混合矩阵。

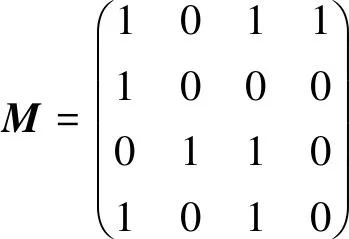
相应地，其逆运算MC-1所用的矩阵表示为：

密钥扩展算法密钥扩展算法具体生成过程如图1所示。对于TK1，在每一圈中，提取前两行的密钥值作为该圈的轮可调密钥，而后经过PT置换操作改变密钥比特块的位置，得到下一圈可调密钥的输入值，其中，

PT=[9,15,8,13,10,14,12,11,0,1,2,3,4,5,6,7]。

TK1中不需要经过线性反馈移位寄存器的操作，而TK2、TK3需要，这里不对TK2、TK3的生成过程进行详细介绍，详见文献[1]。

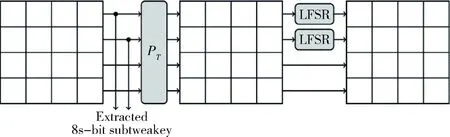
图1 SKINNY算法的密钥扩展过程

1.3 MANTIS算法

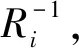
Ri=MixColumns·PermuteCells·AddTweakeyTK·

AddConstants·SubCells

其中S盒变换、P盒置换以及列混合变换的采用与Midori算法相同，具体变换环节见文献[1]，一轮结构如图2所示。

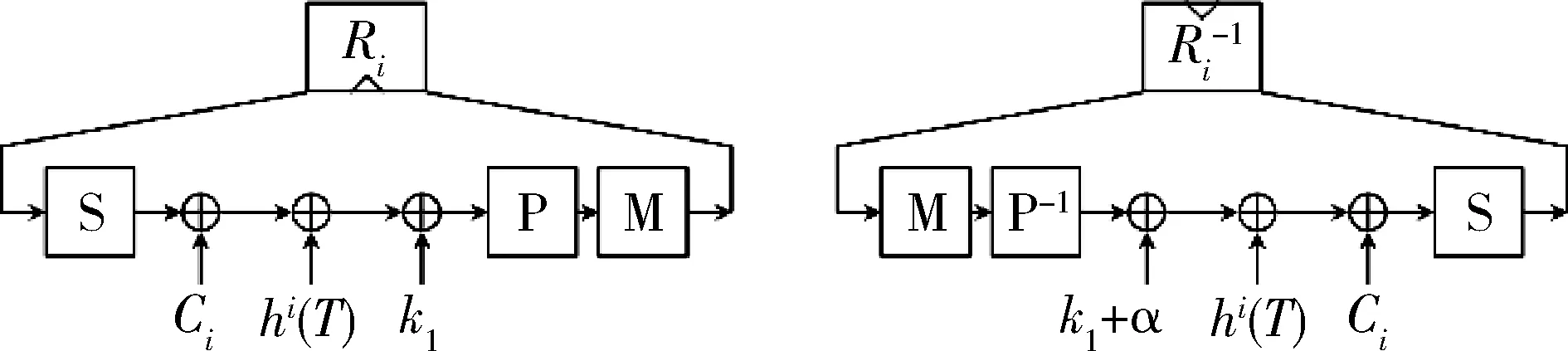
图2 轮函数Ri和的结构图

在算法Rr和Rr+1的中间环节有一个大S盒，可以表示为S·M·S，其中S表示S盒变换，M表示列混合变换。在本文中，将除了输入输出端白化密钥加变换外的其余部分称为MANTISrcore，图3以MANTIS7为例给出了具体算法结构图。

图3 MANTIS算法的结构示意图，以MANTIS7为例

2 SKINNY算法的相关密钥不可能差分区分器构造

本节中首先具体介绍SKINNY算法轮函数以及密钥扩展算法的相关性质，而后依此构造了13轮SKINNY-n-n算法的相关密钥不可能差分区分器。构造得到的区分器分为两类，一类其输入输出状态均仅有一个比特块差分活动，另一类区分器在输入状态仅有一个差分活动块时，其输出状态在同一列有三个比特块差分活动，且这两类区分器的每一类均有两种等价情况，具体过程将在第2.2节中进行介绍。

2.1 SKINNY-n-n算法相关性质

性质1[5]在每一轮变换中，密钥加变换可以和移位变换以及列混合变换操作交换顺序，即将输入状态先进行移位变换以及列混合变换，而后将得到的状态与该轮密钥的等效密钥进行异或，不改变运算结果。

性质2若列混合变换MC的输入状态仅在第1或第3行存在1个比特块活动差分，则输出状态仅有1个比特块差分活动；反之，若列混合变换的逆变换的输入状态仅在第0或第4行存在1个比特块的活动差分，则输出状态也仅有1个比特块差分活动。

证明分析算法的列混合变换矩阵可得，矩阵仅在第1列和第3列有1个1，该两列其余位置取0，则根据矩阵运算规则可得，输入状态若仅在第1行或第3行存在1个差分活动比特块时，运算结果即输出状态定仅有1个比特块差分活动；同理可得，其逆变换矩阵仅在第0列和第2列有1个1，该两列其余位置取0，则输入状态若仅在第0行或第2行存在1个比特块差分活动，此时输出状态也仅有1个比特块差分活动。

证毕。

性质3[5]在对SKINNY算法进行密钥恢复攻击时，由于算法列混合变换所用的矩阵不是MDS矩阵，不仅需要知道活动差分比特块位置处的差分值，还需知道该位置比特块的具体取值。因而不仅需要猜测活动差分比特块位置处的密钥值，对于部分差分值为0位置处的密钥值也需进行猜测。

性质4对于SKINNY-n-n算法，其密钥扩展算法为一个16圈的循环。

证明根据SKINNY-n-n算法密钥扩展方式中PT置换操作的运算规则有TKi+16=PT(TKi)，即构成一个周期为16的循环。具体的各轮密钥中各个位置处的密钥与主密钥的对应关系见图4。

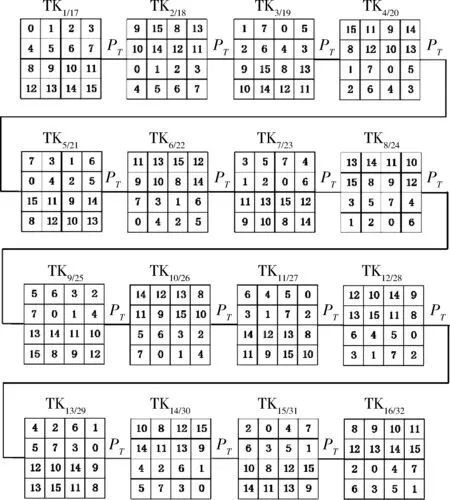
图4 SKINNY-n-n算法密钥扩展方式的周期性

证毕。

性质5[9](S盒性质)对于确定的S盒，随机给定S盒的一对输入输出差分对应时，则平均可以确定S盒的一对输入输出。

2.2 13轮相关密钥不可能差分区分器

SKINNY算法使用较为简单的密钥扩展算法，并且在算法设计者对算法进行介绍时，分析得出不可能差分攻击、相关密钥攻击对算法均有较好的攻击效果，因此本文结合相关密钥攻击和不可能差分分析这两种方法，对SKINNY算法进行了安全性分析。考虑到要使得攻击的轮数尽可能多，就须控制使得活动S盒的数目尽可能少。因此结合性质2和性质4，通过选取特定的明文差分，使得其与某一轮的相关可调密钥差分进行抵消，则可以获得较少的活动S盒，实现差分传递链尽可能地长。

本节中，通过对性质2和性质4的运用，找到了两类长度为13轮的SKINNY-n-n算法的相关密钥不可能差分区分器，与现有的分析结果相比，这两类区分器是攻击长度最长的区分器，下面对这两类区分器进行介绍。

第一类区分器：这类区分器分为两种情形，特点表现在其输入输出状态均为仅有一个比特块差分活动。第一种情形，选取区分器的输入状态仅在ΔY4[3]处存在差分，轮密钥仅在TK4[3]处存在差分，并且两者差分值相等，均为0x1。则其在经过13轮加密后，得到的输出状态仅在ΔY17[11]存在差分，且差分值为0x1是不可能的。第二种情形与第一种情形相似，选取区分器的输入状态仅在ΔY4[0]处存在差分，主密钥仅在TK[7]即轮密钥TK4[0]处存在差分，且ΔY4[0]=ΔTK4[0]=0x1。则其在经过13轮加密后，得到的输出状态仅在ΔY17[8]=0x1是不可能的。

第二类区分器：这类区分器同样也是两种情形，但与第一类区分器不同的是，该类区分器在输入状态仅有一个差分活动块时，其输出状态在同一列有三个比特块差分活动。第一种情形中，选取区分器的输入状态仅在ΔY4[1]处存在差分，轮密钥仅在TK4[1]处存在差分，并且两者差分值相等，均为0x1。则其在经过13轮加密后，得到的输出状态仅在ΔY17[3,7,15]差分活动是不可能的。第二种情形与第一种情形相似，选取区分器的输入状态仅在ΔY4[2]处存在差分，轮密钥仅在TK4[2]处存在差分，且ΔY4[2]=ΔTK4[2]=0x1，则其在经过13轮加密后，得到的输出状态仅在ΔY17[1,5,13]差分活动是不可能的。

上述两类区分器均可以用来进行对SKINNY-n-n算法进行相关密钥不可能差分分析，但运用第一类区分器进行攻击所需的复杂度与第二类区分器相比较少，因此下文中主要运用第一类区分器的第一种情形，给出SKINNY-n-n算法的密钥恢复攻击结果，如图5(a)所示。图5中(a)、(b)分别表示第一类和第二类区分器中的第一种情形，分别记为区分器1.1和区分器2.1。

3 19轮SKINNY-n-n算法的相关密钥不可能差分攻击

本节中首先介绍基于区分器1.1对SKINNY-64-64进行相关密钥不可能差分攻击的具体过程，而后类似地给出对SKINNY-128-128的安全性分析结果。攻击总共分为两个部分：数据收集阶段以及密钥恢复阶段，其中，数据收集部分由两个步骤构成，密钥恢复阶段由7个步骤构成。

3.1 SKINNY-64-64算法的相关密钥不可能差分分析

(1)构造明文结构，使得每个明文结构由216个明文构造而成，其中，在第(5,7,10,13)个半字节遍历所有的可能值，其余位置取定值，则使得每个明文结构产生的231个明文对满足对应的输入差分ΔP=(0,0,0,0,0,*,0,*,0,0,*,0,0,*,0,0)。

(2)在ΔTK=(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0x1,0)的条件下加密明文对，得到相应的密文对，筛选出密文在ΔW19=[2,4,5,7,10,11,13,15]差分值为0，其余位置差分活动，取值不确定的明文，选择2n个这样的明文结构，则攻击所需的明文量为2n+16，得到的对应明文对2n+31×2-32=2n-1个。

(3)计算得到TK19[1,5]，猜测密钥TK19[6]；首先，筛选ΔX19[10]=0x1的明文对，予以保留，此时平均剩余明文对个数为2n-1×2-4=2n-5；而后，由已知ΔY19[9,13]以及Y19[9,13]的值，可计算得ΔX19[9,13]和X19[9,13]，又由ΔX19[1,5,13]有相同的差分值，则根据已知ΔY19[1,5]以及性质5，可确定X19[1,5]和Y19[1,5]的值，再由已知Z19[1,5]、TK19[1,5]=Y19[1,5]⊕W19[1,6]和W18[1]=M-1°X19[5]可计算出TK19[1,5]、ΔW18[1]以及W18[1]的值；而后猜测TK19[6]，计算得Y19[6]，通过S盒的逆运算可得X19[6]；由已知ΔX19[10]=0x1、ΔY19[10]以及Y19[10,14]，利用性质5和S盒的逆运算可得X19[10,14]，进而基于W18[6]=M-1°X19[6,10,14]可计算得W18[6]；最后，由已知ΔY19[11,15]以及Y19[11,15]，筛选ΔX19[11]=ΔX19[15]的明文对，予以保留；则该步骤后，平均剩余明文对的个数为2n-5×2-4=2n-9。

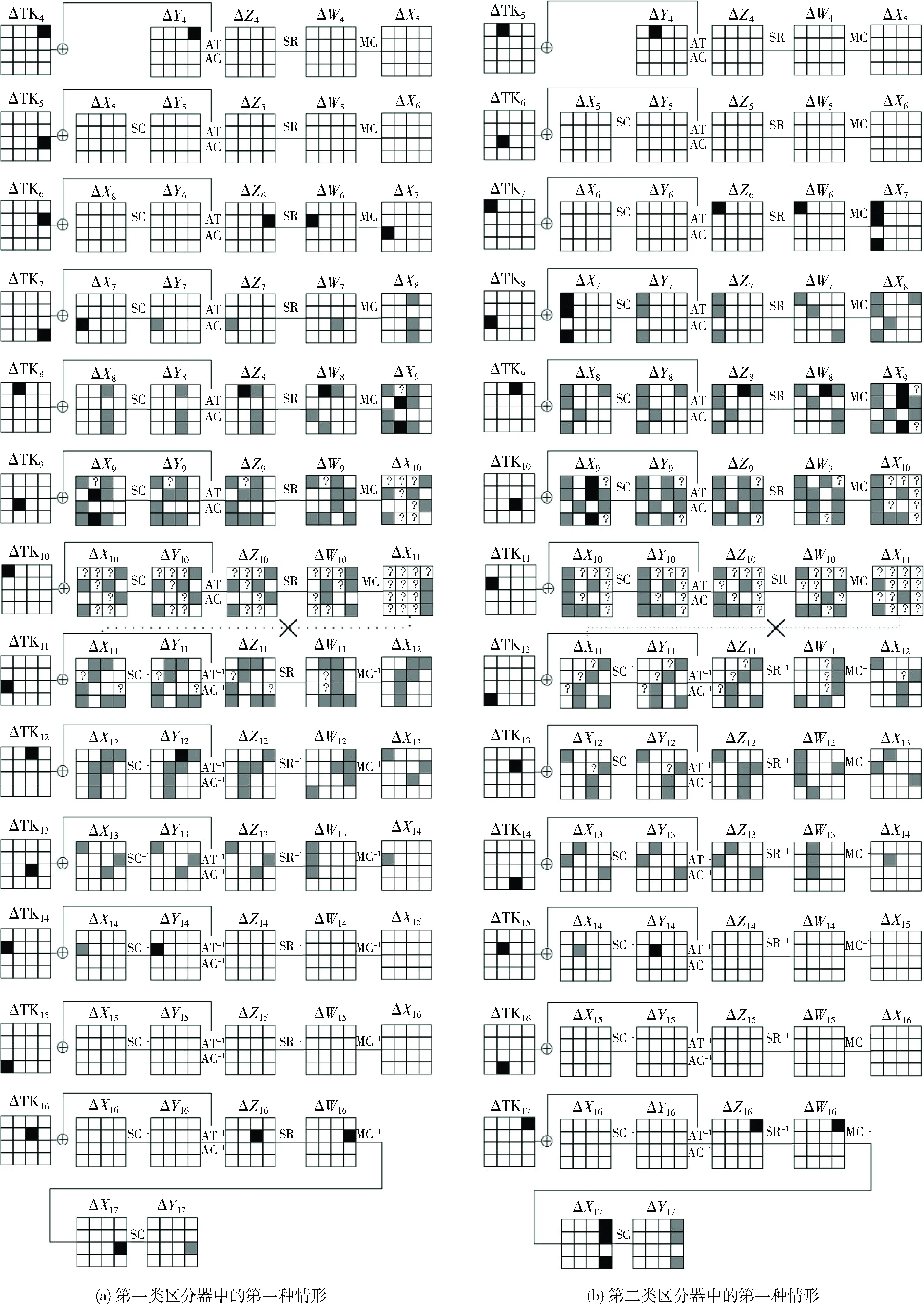
图5 13轮相关密钥不可能差分区分器

(4)计算TK19[3]，猜测密钥TK19[7]；在步骤(3)基础上，已知ΔX19[3]=ΔX19[15]和ΔY19[3]，利用性质5，可确定X19[3]和Y19[3]的值，再由已知Z19[3]可计算出密钥TK19[3]=Y19[3]⊕Z19[3]；猜测密钥TK19[7]，计算得Y19[7]，再由已知Y19[15]，则根据S盒的逆运算可得X19[7,15]，利用W18[11]=M-1°X19[7,15]可计算得ΔW18[11]以及W18[11]的值，则该步骤后，平均剩余明文对的个数仍为2n-9。

(5)猜测密钥TK19[0]；可计算得到ΔY19[0]以及Y19[0]的值，进而可得ΔX19[0]以及X19[0]的值，再由已知Y19[12]，根据S盒的逆运算可得X19[12]，利用W18[12]=M-1°X19[0,12]可得ΔW18[12]以及W18[12]的值，则该步骤后，平均剩余明文对的个数仍为2n-9。

(6)猜测密钥TK18[5]，计算TK18[1]；由步骤(3)～(5)，已计算得ΔW18[1,6,11,12]和W18[1,6,11,12]，进而可求得ΔY18[1,9,13]和Y18[9,13]，利用S盒逆运算，可计算出ΔX18[9,13]，筛选ΔX18[9]=ΔX18[13]的明文对予以保留，则此时平均剩余明文对个数为2n-9×2-4=2n-13；进一步由于ΔX18[1]=ΔX18[9]=ΔX18[13]，利用性质5可确定X18[1]和Y18[1]，即计算得TK18[1]=Y18[1]⊕W18[1]；在此基础上，对密钥TK18[5]进行猜测，基于W17[9]=M-1°X[5,13]，确定ΔW17[9]以及W17[9]，再进行一轮解密，筛选满足ΔX17[11]=0x1的明文对予以保留，则该步骤后，平均剩余明文对的个数为2n-13×2-4=2n-17。

(8)猜测密钥TK2[0,3,4]；在步骤(7)基础上，猜测TK2[0,3,4]，计算得到Z2[0,3,4,10,11,13]的具体值，其中由X3[12]=M°W2[0,8,12]=M°Z2[0,10,13]可求得ΔX3[12]以及X3[12]的值，根据Z2[3]和Z2[4,11]可分别求得X3[3]和X3[9]的值，则该步骤后，平均剩余明文对的个数为2n-29。

(9)由步骤(4)已得TK19[3]，根据密钥扩展的对应关系，即已知TK3[3]，在步骤(8)基础上，计算得ΔZ3[12]以及Z3[3,9,12]的值，进而计算并验证ΔY4[3]=0x1是否成立。若此时仍有明文对通过验证，则说明猜测的密钥错误，将其放入错误密钥候选密钥集。余下的未猜测的16 bit密钥选取一个明密文对进行验证。具体的攻击路径如图6所示。

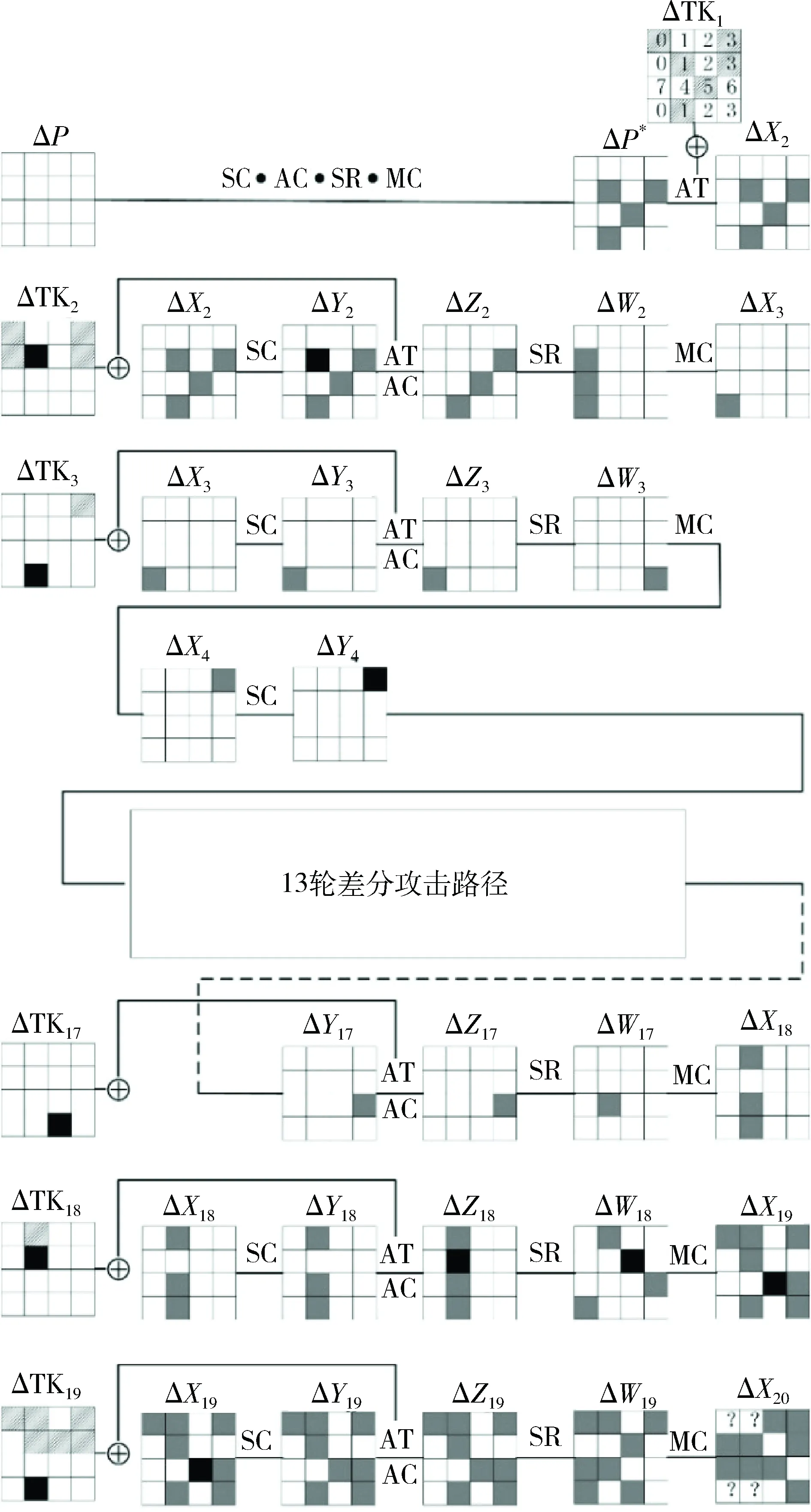
图6 19轮相关密钥不可能差分攻击路径

其中灰色表示活动比特块，白色表示差分为0的比特块，？表示差分值不确定的比特块，差分值为0x1的密钥比特块和状态比特块用黑色表示，条形状表示除具有差分的密钥比特块外的其余需猜测的密钥比特块。攻击所需的复杂度由定理1给出。

定理1根据此攻击，可以恢复出SKINNY-64-64算法的全部密钥比特，攻击所需的数据复杂度为255个选择明文，时间复杂度为240.82次19轮SKINNY-64-64加密，存储复杂度为248。

证明攻击所需的复杂度主要分为数据复杂度、时间复杂度以及存储复杂度三部分。数据复杂度方面，主要由步骤(2)决定，所需选择明文量为2n+16，即数据复杂度为2n+16个选择明文。时间复杂度主要集中在密钥恢复阶段，下面对各步骤所需的时间复杂度进行具体分析。

在步骤(3)中，首先筛选明文对，而后计算得到TK19[1,5]，并对TK19[6]进行猜测，筛选保留符合条件的明文对，则所需的计算复杂度为2n-5×24×2=2n；

在步骤(4)中，根据步骤(3)操作后剩余的2n-9个明文对，首先计算得到TK19[3]，然后猜测密钥TK19[7]，所需的计算复杂度为2n-9×28×2=2n；

在步骤(5)中，根据步骤(4)操作后操作后剩余的2n-9个明文对，对密钥TK19[0]进行猜测，所需的计算复杂度为2n-9×212×2=2n+4；

在步骤(6)中，首先筛选保留满足ΔX18[9]=ΔX18[13]的明文对，计算出密钥TK18[1]，而后猜测密钥TK18[5]，所需的计算复杂度为2n-13×216×2=2n+4；

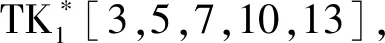
在步骤(8)中，根据步骤(7)中剩余的2n-29个明文对，猜测密钥TK2[0,3,4]，所需的计算复杂度为2n-29×232×2=2n+4；

在步骤(9)中，已知密钥TK3[3]，计算并验证ΔY5[3]=0x1是否成立，若验证满足，仍有明文对通过检验，则说明之前的猜测错误。一个错误猜测无法通过检测的概率为(1-2-4)2n-29，此时已对TK19[0,1,3,5,6,7]，TK18[1,5]，TK1[0]和TK2[0,3,4]共48 bit密钥进行了计算和猜测，要使错误密钥剩余的明文对足够少，即有N=248×(1-2-4)2n-29≤1，得n≈39，该步骤得计算复杂度为2n-29×232×2=2n+4。总计，攻击所需的计算复杂度为：

综上可得，攻击所需的数据复杂度为255个选择明文，计算复杂度为240.82次19轮SKINNY-64-64加密，存储复杂度主要在于存储明文结构及错误密钥，则所需的存储复杂度为248。

证毕。

3.2 SKINNY-128-128算法的相关密钥不可能差分分析

上面介绍了运用第2.2节构造得到的13轮相关密钥不可能差分区分器对SKINNY-64-64实施攻击的具体过程。同样地，该攻击步骤对于SKINNY-128-128算法也适用，但由于在这两种密钥规模的SKINNY算法中每一比特块对应的比特数一个为4，另一个为8，因此在攻击选择明文量、每一步骤操作后剩余明文对数目以及攻击所需复杂度方面，二者有较大不同。所以，在这里，不再赘述针对SKINNY-128-128在密钥恢复阶段的具体攻击步骤，只介绍每一步骤后剩余的明文对数目以及恢复的密钥比特，并分析攻击所需复杂度。

与第3.1小节的攻击类似，在数据收集阶段，每个明文结构由232个明文构造而成，即其在第(5,7,10,13)个字节遍历所有的可能值，其余位置取定值，选择初始密钥在ΔTK=(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0x1,0)的条件下加密明文对，得到相应的密文对，筛选出密文在ΔW20[2,4,5,7,10,11,13,15]差分值为0，其余位置差分活动，取值不确定的明文，则选择2n个这样的明文结构，得到的对应明文对2n+63×2-64=2n-1个，即攻击所需的明文量为2n+32。下面通过表4介绍密钥恢复阶段每一步骤的具体情况，攻击所需复杂度由定理2给出。

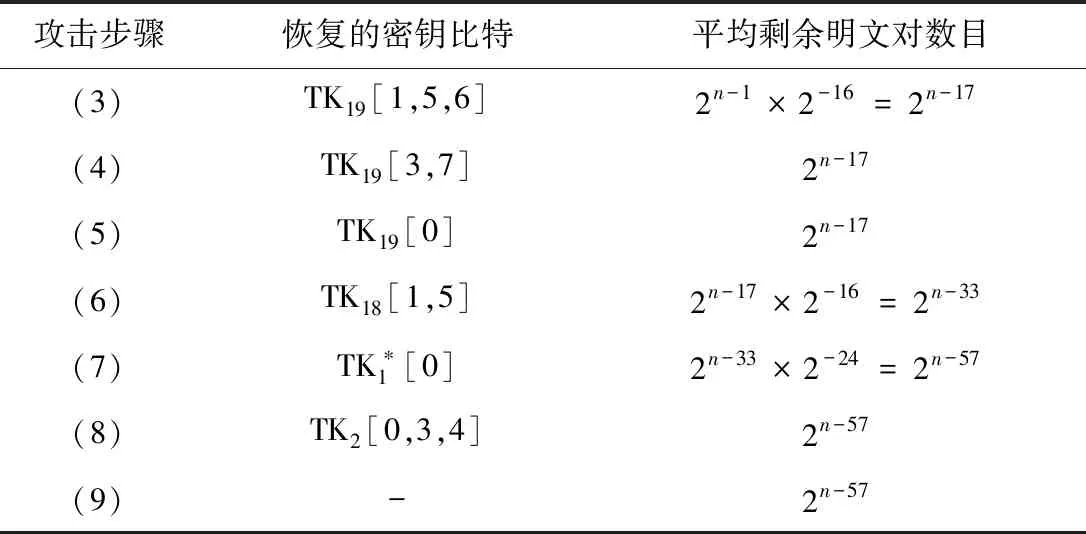
表4 SKINNY-128-128密钥恢复阶段的具体情况

定理2根据此攻击，可以恢复出SKINNY-128-128算法得全部密钥比特，攻击所需的数据复杂度为2104个选择明文，时间复杂度为277.76次19轮SKINNY-128-128加密，存储复杂度为296。

证明同定理1证明类似，攻击所需的复杂度主要分为数据、时间以及存储复杂度三部分。数据复杂度方面，同样地主要由步骤(2)决定，所需选择明文量为2n+32，即数据复杂度为2n+32个选择明文。时间复杂度主要集中在密钥恢复阶段，下面简要分析介绍各步骤所需的时间复杂度。

步骤(3)所需的计算复杂度为2n-9×28×2=2n；步骤(4)所需的计算复杂度为2n-17×216×2=2n；步骤(5)所需的计算复杂度为2n-17×224×2=2n+8；步骤(6)所需的计算复杂度为2n-25×232×2=2n+8；步骤(7)所需的计算复杂度为2n-41×240×2=2n；步骤(8)所需的计算复杂度为2n-57×264×2=2n+8；在步骤(9)中，一个错误猜测无法通过检测的概率为(1-2-8)2n-57，要使错误密钥剩余的明文对足够少，即有N=296×(1-2-8)2n-57≤1，得n≈72，该步骤得计算复杂度为2n-57×264×2=2n+8。总计，攻击所需的计算复杂度为：

综上可得，攻击所需的数据复杂度为2104个选择明文，计算复杂度为277.76次19轮SKINNY-128-128加密，存储复杂度为296。

证毕。

4 MANTIS算法的相关密钥差分特征

在本节中，通过分析MANTIS算法的结构特性，利用相关密钥分析技术，结合差分类分析方法，找到了可用于对该算法进行安全性分析的几类高概率相关密钥差分类区分器。首先，与PRINCE算法[10]类似，介绍基于算法α映射的性质，得到的一种针对全轮MANTIS算法的平凡的相关密钥差分特征；而后，根据找到的一类特殊的一轮循环区分器，构造出了一类针对MANTISrcore的相关密钥矩阵攻击区分器，其中1≤r≤6；最后，通过选取特殊的可调差分，构造得到了针对MANTIS5可进行实际攻击的一种改进的相关密钥差分特征。

4.1 基于α映射的平凡相关密钥差分特征

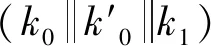
其中，X1、X2表示P1、P2经过白化密钥后的MANTIScore的输入，Y1、Y2表示C1、C2经过白化密钥逆运算后的MANTIScore的输出。

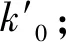
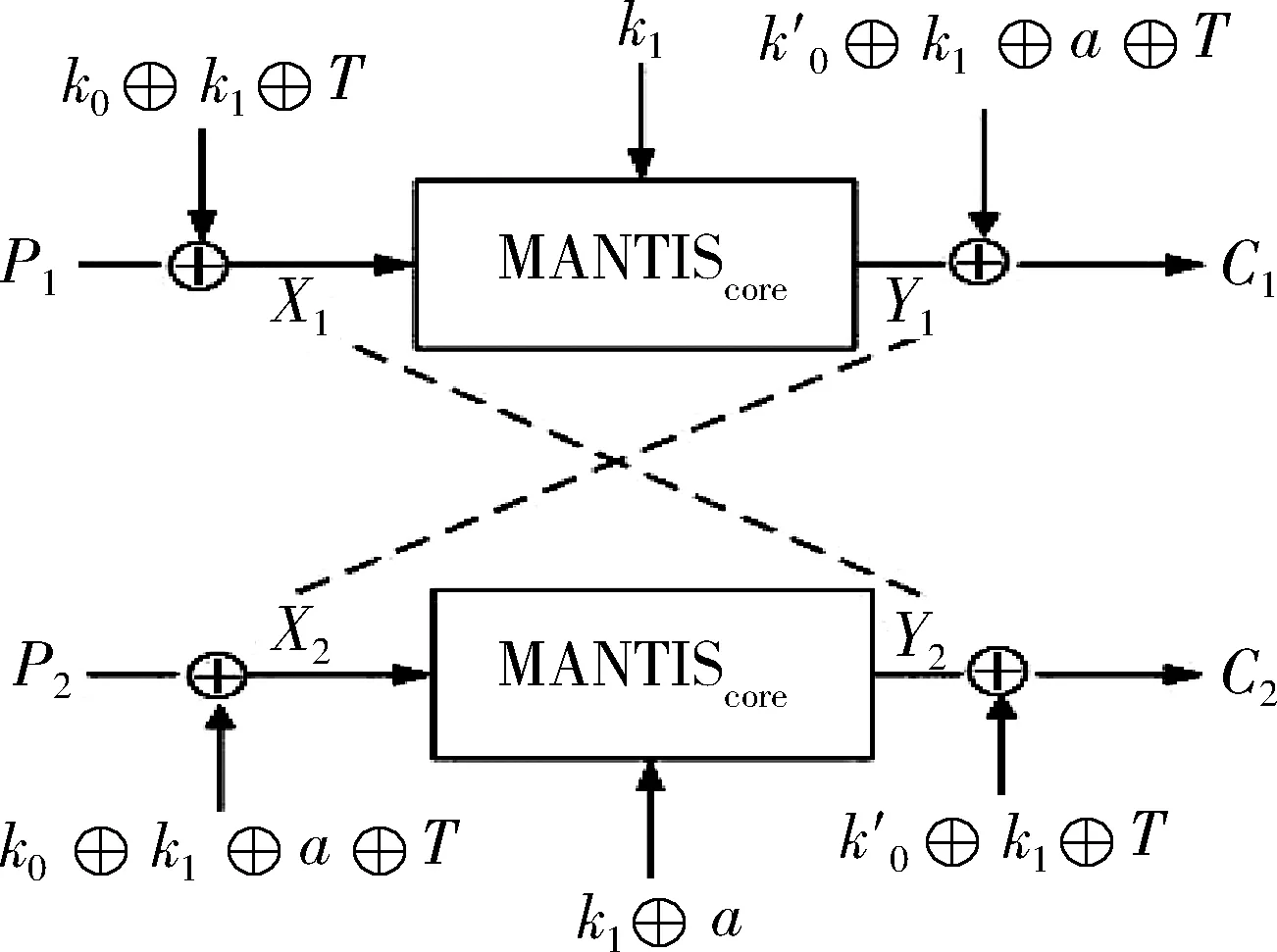
图7 基于α映射的平凡相关密钥差分

4.2 针对MANTISr core的相关密钥矩阵攻击区分器

通过分析算法的结构特性可得，要想使得对算法进行攻击的轮数足够多，则就需要使得活动差分比特块的数量足够少。基于此思想，将MANTISrcore分为E0和E1两部分，其中E0表示MANTISrcore的前r-1轮，E1表示MANTISrcore的剩余加密环节。通过对E0、E1分别找到一条高概率的差分路径，两者结合，从而构造得到了一类针对MANTISrcore的相关密钥矩阵攻击区分器。

定理3通过将算法分为E0和E1两部分，构造得到了一类针对MANTISrcore的相关密钥矩阵攻击区分器，区分器概率为2-8r-12.36，其中r≤6。

证明对于E0部分，主要使用的是一种特殊的一轮区分器，对其迭代r-1轮，得到E0的一条高概率差分路径。首先根据算法S盒变换的差分分布表，选取进行一轮S盒变换时，输入输出在具有相同差分时，其概率达到S盒的最大概率2-2的差分值。经过筛选，得到候选的差分值为{0xa,0xb,0xe,0xf}。在这里，为了使得E1部分的概率最大，选取输入的差分值为0xa。此外，考虑使用的相关密钥差分比特块较少，选定明文输入差分仅在第1个半字节存在，即ΔX=(0,0xa,0,0,0,0,0,0,0,0,0,0,0,0,0,0)。而后，选取密钥差分，使得经过PT变换和列混合变换后的输出ΔXMC=ΔX=(0,0xa,0,0,0,0,0,0,0,0,0,0,0,0,0,0)。在这里，选取Δk=(0,0,0,0,0xa,0,0,0,0,0,0,0,0,0,0xa,0)，由此构造得到了可用于迭代的一轮区分器，且该区分器的概率为2-2。将此区分器再向下迭代r-2轮，即得到了E0的一条概率为2-2(r-1)差分路径，具体一轮区分器如图8所示。

图8 E0部分的一轮区分器

E1部分，主要由第r轮、中间环节大S盒以及后r轮组成，每一轮均使用相同的相关密钥，即Δk=(0,0,0,0,0xa,0,0,0,0,0,0,0,0,0,0xa,0)。第r轮与部分的区分器结构相似，所不同的是使得其经过S盒变换的输入与输出差分值不同，即输入差分为0xa，输出差分ΔXSBr∈{0x5,0xd,0xf}，其中任一种概率均为2-2。选取S盒的输出差分为其中任一种情况，则在经过一轮变换后的状态ΔXMCr在第(1,9,13)个半字节存在差分，也就是ΔXMCr=(0,*,0,0,0,0,0,0,0,t,0,0,0,t,0,0)，其中*∈{0x5,0xd,0xf},t=*⊕0xa。对于后r轮的第一轮，采用与第r轮同样的方法，使得其经过S盒变换后的输出差分为0xa，但输入差分ΔXSBr∈{0x5,0xd,0xf}，其中任一种情况的概率也为2-2，则经过密钥加变换和PT变换的逆变换后的状态ΔXPTr在第(5,9,13)个半字节存在差分，即：

ΔXPTr=(0,0,0,0,0,*,0,0,0,0xa,0,0,0,0xa,0,0)

其中*∈{0x5,0xd,0xf}。余下的r-1轮与前r-1轮相同，均采用一轮区分器进行r-1轮迭代。所以当大S盒的输入为

ΔXMCr=(0,*,0,0,0,0,0,0,0,t,0,0,0,t,0,0)

输出为ΔXPTr=(0,0,0,0,0,*,0,0,0,0xa,0,0,0,0xa,0,0)。通过编程实验验证，当且仅当大S盒输入输出中*的取值相同时，差分路径才能成立，且所求得概率在取不同的*值时，也不全相同。当*=0x5、0xf时，大S盒以及其前后两轮差分路径成立的概率均为2-2×2-7.41×2-2；当*=0xd时，路径成立概率为2-2×2-9×2-2。所以进行求和可得该路径成立的最终概率为2-10.18，余下的利用一轮区分器迭代r-1轮的概率为2-2(r-1)。则E1部分的该差分路径概率为2-10.18×2-2(r-1)=2-8.18-2r。

综上，利用E0部分和E1部分的两条高概率差分路径，可以构造得到一类针对MANTISrcore的相关密钥矩阵区分器。该区分器的概率为(2-2(r-1)×2-8.18-2r)2=2-8r-12.36。又有算法分组规模为264，因此要使得2-8r-12.36>2-64，则1≤r≤6。图9给出了具体的相关密钥矩阵区分器的示意图。

证毕。

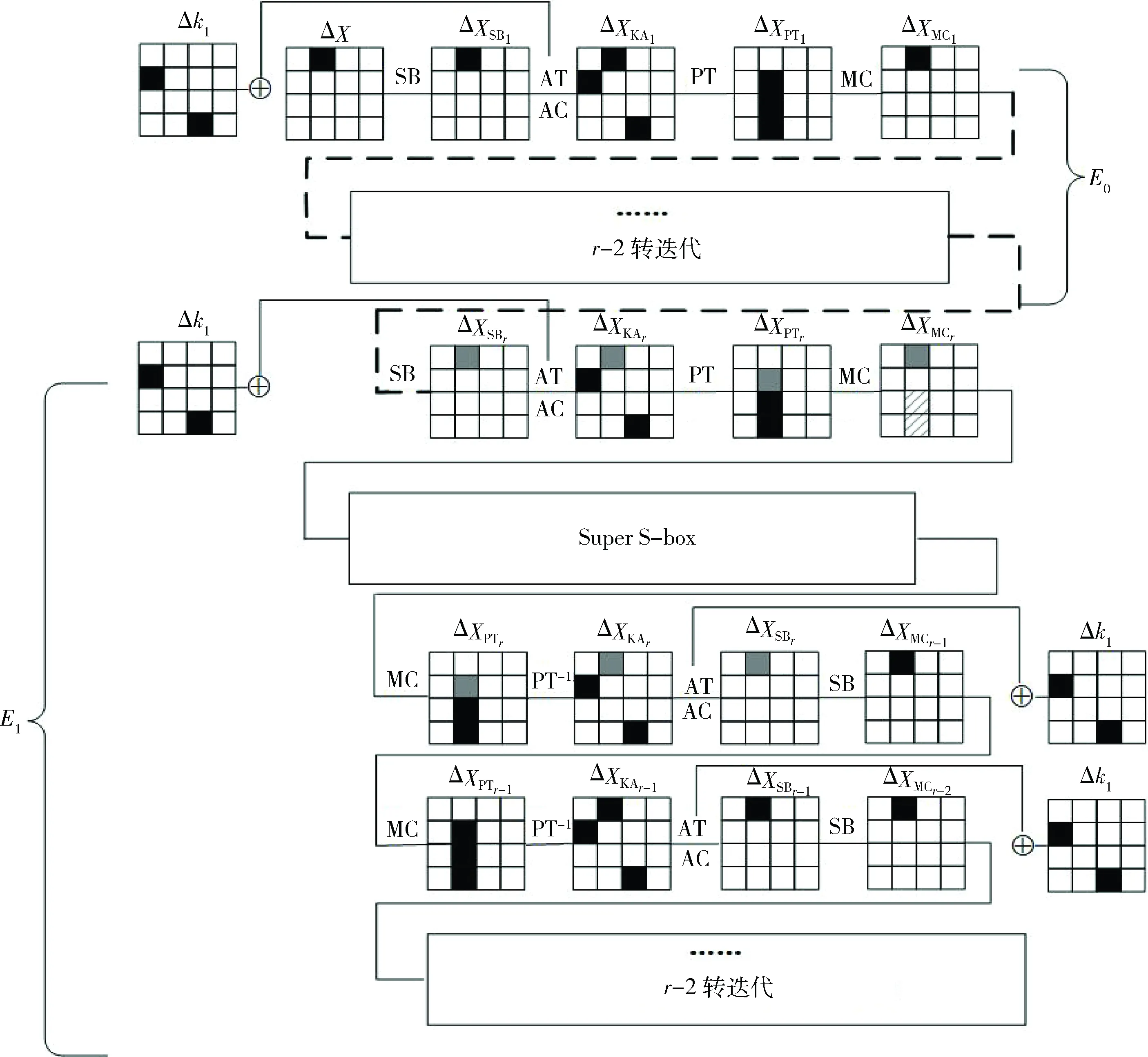
图9 MANTISr core的相关密钥矩阵攻击区分器

4.3 MANTIS5的改进相关密钥差分特征

在文献[8]中提出了一种针对MANTIS5的实际密钥恢复攻击。其主要利用密钥扩展算法中的可调密钥，给出了算法的一类相关密钥截断差分区分器，并使得该特征的概率与设计者提出的最优差分概率相匹配，即最优差分概率2-34×2=2-68。而本小节中，利用在特定位置选取相同的密钥差分和可调差分，构造得到了一种改进的相关密钥差分特征，提高了差分概率。

在这里，选取密钥k1在第4个半字节存在差分，且差分值为0xa，初始可调ΔT在第14个半字节存在差分值为0xa的差分。则由图9可得，观察差分特征在第3轮的状态，使得经过第3轮S盒变换后状态为

ΔXSB3=(0xa,0,0,0,0xa,0,0,0,0,0,0,0,0,0,0,0)

此时密钥差分为

Δk1⊕Δh3(T)=(0xa,0,0,0,0xa,0,0,0,0,0,0,0,0,0,0,0)

刚好差分抵消，再进行下一轮。在第4轮变换中，密钥差分与可调差分存在的位置相同，差分同样也相互抵消。因此，直到第5轮的密钥加变换后的状态存在差分，即:

ΔXKA5=(0,0,0,0,0xa,0,0,0,0,0,0,0xa,0,0,0,0)。

而后再进行接下来的轮变换。得到大S盒变换后的状态与ΔXMC5的状态相同。根据算法的FX结构性质，类似地可对第6～8轮进行相同构造。差分路径如图10所示。

根据编程验证，上述步骤较文献[8]中构造的区分器概率由2-40.51提高到了2-28.35，具体的每一轮的差分概率在此进行具体介绍。在第1轮输入状态选取明文差分，使得其经过初始密钥变换后的状态为

ΔP′=(*,0,*,*,*,0,0,0,0,0,*,0,*,0,0,0),*∈{0x5,0xa,0xd,0xf}，则经过S盒变换得到

ΔXSB1=(*,0,0xa,*,0xa,0,0,0,0,0,*,0,*,0,0,0),*∈{0xa,0xf},且ΔXSB1[0]=ΔXSB1[10]、ΔXSB1[3]=ΔXSB1[12]，其中该轮的概率为

在第2轮S盒变换的输入由第一轮可得，即

ΔXMC1=(*,0,0,0,*,0,*,0,0,0,*,0,0,0,0,0),*∈{0xa,0xf},

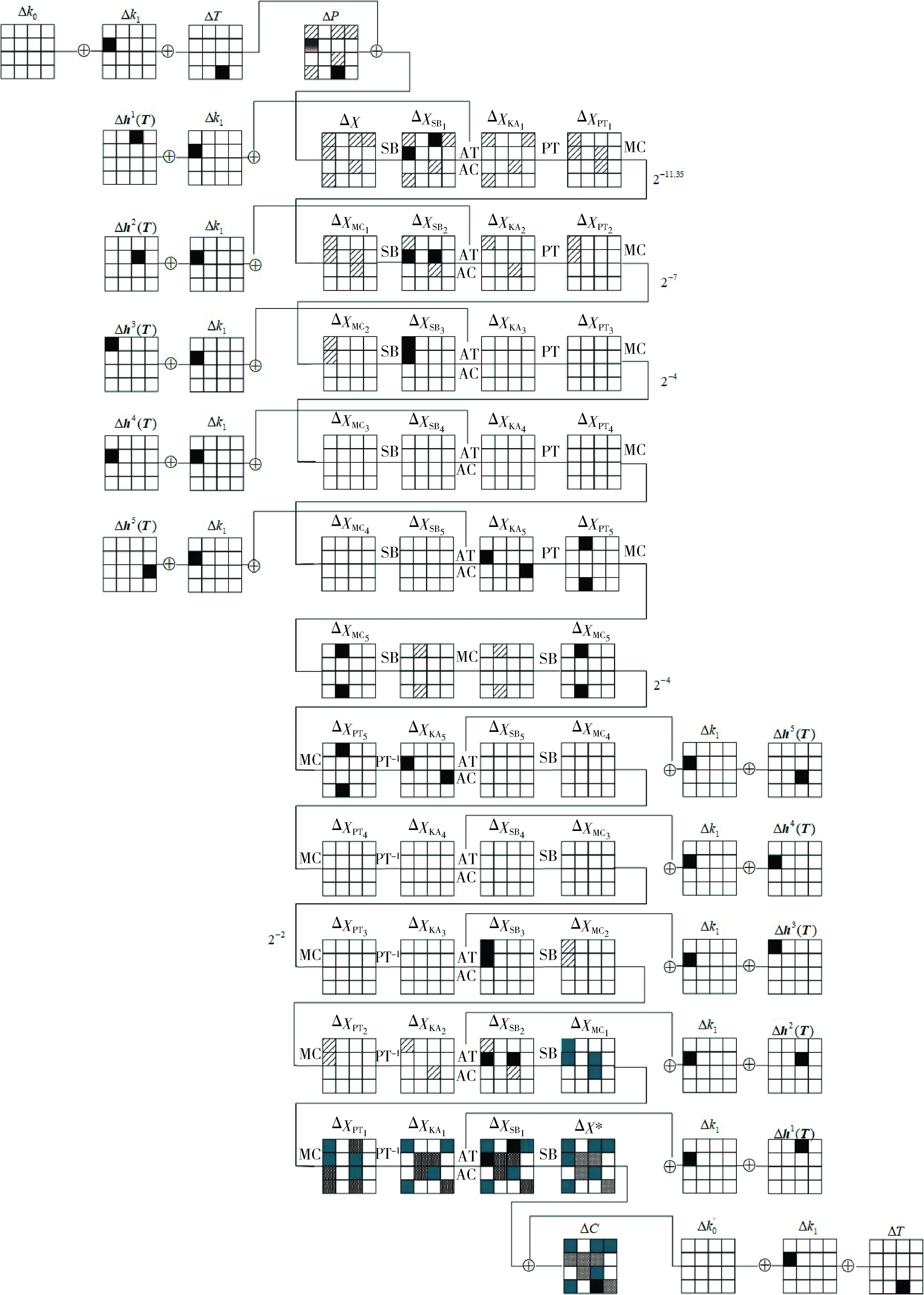
图10 MANTIS5相关密钥差分特征

同一列的两比特块差分值相同。则变换后的状态为使得其在第4、6个半字节差分值为0xa，第0、10半字节差分值相同，且取值属于{0xa,0xf}，则该轮的概率为2-2×2×(2-4+2-4)=2-7。第3轮变换中，当S盒输入差分为0xa或0xf时，得到输出差分为0xa的概率为2-2，因而第3轮变换的概率为2-4。大S盒的概率同样也为2-4，后5轮变换的概率计算与前5轮类似。综上，该区分器的概率为2-11.35×2-7×2-4×2-4×2-2=2-28.35。

从而根据上述步骤得到了针对MANTIS5的一类改进相关密钥差分特征。进一步地，将MANTIS5的区分器分别拓展1轮或2轮，即可得到对于MANTIS6和MANTIS7的相关密钥差分特征。

5 结论

本文首先通过分析SKINNY算法的密钥扩展方式的Tweakey结构特性以及算法扩散层的结构特点，构造了SKINNY-n-n算法的两类13轮相关密钥不可能差分区分器，并据此给出了对19轮SKINNY-n-n算法的安全性分析结果。其中，对于SKINNY-64-64算法，攻击所需的数据复杂度为255，时间复杂度为240.82，存储复杂度为248。对于SKINNY-128-128算法，攻击所需的数据复杂度、时间复杂度以及存储复杂度分别为2104、277.76和296。而后，针对SKINNY算法族中的低延迟变体MANTIS系列算法，分别给出了设计者提出的基于α映射一类平凡相关密钥差分特征、对于MANTISr core(1≤r≤6)的相关密钥矩阵区分器、对于MANTIS5的一类改进相关密钥截断差分路径，丰富了对于MANTIS系列算法的安全性分析结果。