BEC信道下高维核矩阵极化码的精确设计

黄志亮，张施怡，周水红

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

0 引言

第一个被证明的极化码由Arikan教授提出，它是一种可以在任意的二进制输入离散无记忆信道达到香农容量，并且有着低编译码复杂度和明确设计方法的编码方案[1]。该极化码基于核矩阵

文献[2]的研究表明，核矩阵G2可以被一个高维核矩阵Gm,m≥3替代，替代的极化码有着更快的极化速率。目前，研究者们已经设计出了大量具有更大极化速率的高维核矩阵[3-7]。

显然，要使用高维核矩阵极化码，首先就要设计出相应的极化码。一个很自然的思路就是将G2核矩阵极化码的设计方法推广至高维核矩阵。目前，G2核矩阵极化码的设计方法包括：① 高斯近似—密度进化方法(GA-DE)[8-11]；② Tal-Vardy的上/下近似方法[12]；③ 基于BEC信道下的设计方法[13]。GA-DE方法和Tal-Vardy的上/下近似方法的直接推广分别存在各种问题。本文将基于BEC信道下的设计方法从G2核矩阵推广至高维核矩阵极化码的设计。

极化码的设计步骤较明确，但只在BEC信道下的设计才是有效的[1]。文献[13]将BEC信道下的设计2×2维核矩阵极化码的方法推广到任意二进制高维核矩阵极化码设计中，通过近似计算出位信道的擦除概率来完成极化码的设计。本文给出一种BEC信道下高维核矩阵极化码擦除概率的精确设计方法，通过擦除概率多项式准确递归计算出位信道的擦除概率，从而完成高维核矩阵极化码的精确设计。

1 极化码的简单回顾

首先给出高维核矩阵极化码的定义，然后简要描述BEC信道下设计2×2维核矩阵极化码的方法。

1.1 极化码

考虑一个简单的擦除概率为ε的BEC信道W，如图1所示。

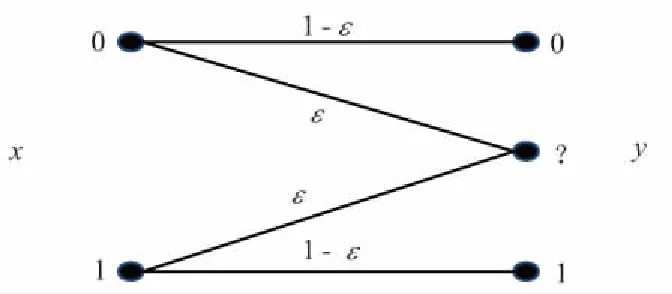
图1 擦除概率为ε的BEC信道

其输入集合为{0,1}，输出集合为{0,1,?}，转移概率为：

W(0|0)=W(1|1)=1-ε,
W(？|0)=W(？|1)=ε,
W(1|0)=W(0|1)=0。

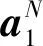
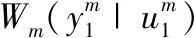
(1)

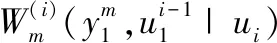
(2)

1.2 基于BEC信道的极化码设计

在2×2维极化码设计时，BEC信道下位信道的擦除概率递归计算式为[1]：

(3)

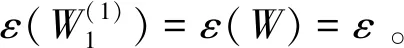
Arikan在文献[14]中提出了一个基于BEC信道的二维核矩阵极化码的启发式设计方法。给定一个信道W，假定其信道容量为C，则该启发式极化码设计方法如下：

① 令擦除概率ε=1-C的BEC信道为这个信道的配对信道;

② 在该ε的BEC信道下设计极化码：根据式(3)递归计算出最后一层位信道的擦除概率，并按擦除概率对位信道进行排序，选择出信息位和冻结位集合，即极化码。

2 BEC信道下高维核矩阵极化码设计

类比于2×2维核矩阵，BEC信道下高维核矩阵极化码设计的关键点是：第n～n+1层的擦除概率的有效计算。研究表明，BEC信道下高维核矩阵的位信道同样是BEC信道，并且第n+1层位信道的擦除概率可以通过第n层位信道的擦除概率组成的一个多项式计算获得。

首先给出高维核矩阵的单步位信道为BEC信道的证明，其次给出单步递归位信道的擦除概率计算多项式，最后给出BEC信道下的高维核矩阵极化码设计算法。

2.1 单步递归位信道为BEC信道的证明

文献[15-16]中提出一个l-表达式，l-表达式将单步递归位信道的似然比表示为原信道似然比的一个公式，该公式中只有3种操作：◇，×，⊗操作。因此，只需要证明经过这3种操作后的信道仍然是BEC信道，那么当原始信道为BEC信道时，对于任意的核矩阵Gm，其对应的位信道也为BEC信道。

定理1：任意核矩阵Gm的单步递归位信道也为BEC信道。

证明：首先证明2个BEC信道经过◇操作后的信道仍然是BEC信道。

给定一个BEC信道W，假设其擦除概率为ε。根据BEC信道的转移概率可得，其似然比取值和概率质量分布如下：

(4)

令l1，l2,l同分布且相互独立，则◇操作符定义为:

(5)

根据式(4)和式(5)得，l1◇l2的概率质量分布如表1所示。

表1l1◇l2的概率质量分布

(l1,l2)l1◇l2P(+∞,+∞)+∞14(1-ε)2(+∞,1)112ε(1-ε)(+∞,0)014(1-ε)2(1,+∞)112ε(1-ε)(1,1)1ε2(1,0)112ε(1-ε)(0,+∞)014(1-ε)2(0,1)112ε(1-ε)(0,0)+∞14(1-ε)2

将l1◇l2取值相同的概率值相加，即(+∞,+∞)和(0,0)合并看成为+∞，将(+∞，0)和(0，+∞)合并看成为0，其他元素合并看成为1，则有

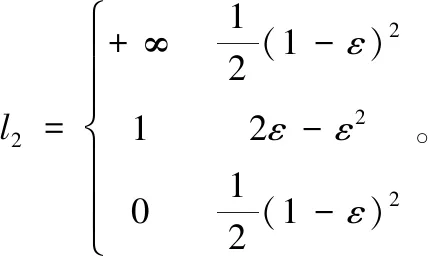
(6)

显然，根据式(6)，l1◇l2可看成为擦除概率为2ε-ε2的BEC信道。

×操作和⊗操作的证明过程类似于◇操作，这里不再叙述。同理可证明2个BEC信道经过×操作和⊗操作后的信道是BEC信道。

因此，定理1得证。

2.2 单步递归位信道擦除概率多项式

由上述内容可知，将l-表达式计算结果为1的概率值相加就是该单步位信道的擦除概率。因此，获得单步位信道擦除概率多项式最简单的方法是给定一个l-表达式，将每一个可能的输入带入l-表达式，如果最后计算结果为1，将该输出概率加入该位信道的擦除概率，最后累加出来的值就是该位信道的擦除概率。显然该概率值为原始信道擦除概率的一个多项式，称之为单步递归位信道擦除概率多项式。

例如，初始BEC信道的擦除概率为ε，对于文献[4]给出的G6和G7核矩阵，其单步递归位信道的擦除概率多项式分别为：

(7)

(8)

2.3 BEC信道下的高维核矩阵极化码设计

BEC信道下高维核矩阵极化码的设计步骤如下：① 根据单步递归位信道擦除概率多项式递归计算最后一层位信道的擦除概率；② 对最后一层的擦除概率由小到大排序，挑选出最小的K个位构成信息位集合，即完成了极化码的设计。算法1给出基于BEC信道的极化码设计算法。

算法1：基于BEC信道的极化码设计算法

1：输入码长N，码率R，初始BEC信道W的擦除概率ε，存储各层擦除概率值的二维数组Q

2：输出：信息位集合A

3：获取单步递归多项式，并记其为f(i),i=1,…,m

4：Q[0]初始化长度为1，且Q[0][0]=ε

5：fori=1,2，…,ndo

6：Q[i]初始化长度为mi

7： forj=0,1,…,mi-1-1 do

8： fork=0,1,…,m-1 do

9：Q[i][m*j+k]=f(k)[Q[i-1][j]]

10： end

11： end

12：end

13：forl=0,1，…,Ndo

14：Pe[l]=Q[m][l]

15：end

16：依据Pe(N)，选择K个最少的错误索引作为A

17：输出A

算法1中f(k)表示第k个位信道的擦除概率多项式，它是擦除概率ε的一个多项式。而f(k)[Q[i-1][j]]是指将f(k)所表示的多项式中的所有ε替换为一个实际的值Q[i-1][j]，然后计算获得一个最终值。

3 仿真结果

首先给出参数ε的最优设置方法，然后给出基于BEC信道下设计的高维核矩阵极化码的译码性能。

3.1 最优参数选择

在算法1中，参数ε最优取值需要确定。Arikan直接令ε=1-C，C为初始信道的信道容量。然而实验结果表明该方法得到参数ε并不能设计出最优的极化码。本小节给出一种量化测试的方法来确定最优的ε，参数ε的取值范围为[0,1]，以步长0.1或0.05取有限个点，在固定为1.5 dB时，比较所有设计极化码的译码性能，则具有最优性能的点即为参数ε的最优值。

在不同ε下基于BEC信道设计方法设计出的极化码的误帧率(FER)和信噪比(Eb/N0)的仿真图如图2所示，码率为1/2，码长为4 096的G16核矩阵。

图2 不同ε下设计的极化码的FER比较

3.2 BEC信道下设计的极化码的译码性能

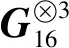
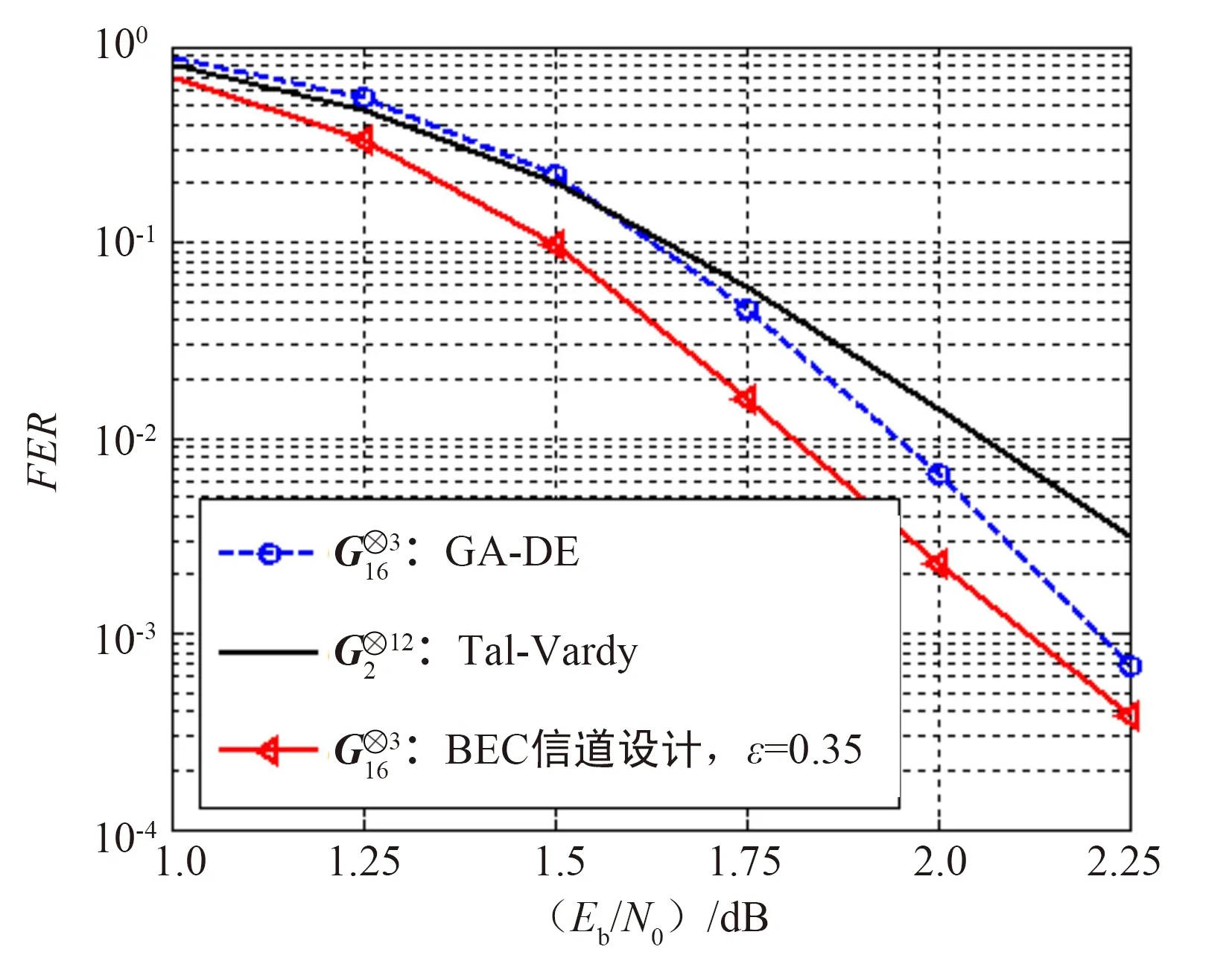
图3 基于BEC信道和GA-DE设计极化码的FER 比较

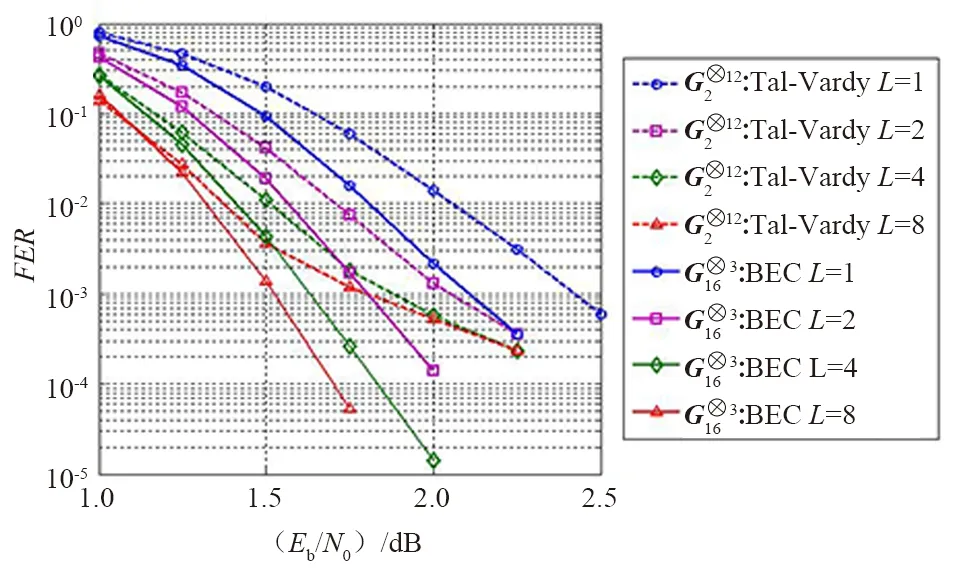
图和极化码的FER比较

由图可知，在LSC译码下，基于ε=0.35的BEC信道下设计的高维核矩阵极化码比原2×2核矩阵有更低的误帧率。

仿真表结果明，基于BEC信道的极化码设计方法明显优于GA-DE方法。同时，基于BEC信道设计方法设计的高维核矩阵极化码优于同等码长和码率下的G2核矩阵极化码。

4 结束语

本文提出了一种基于BEC信道下设计高维核矩阵极化码的方法，给定一个任意的高维核矩阵Gm，首先证明了单步递归位信道仍然为BEC信道；然后根据l-表达式获得了单步递归位信道的擦除概率多项式。

依据所获得的单步递归位信道的擦除概率多项式，Gm极化码设计方法为：由擦除概率多项式递归求出最后一层的概率，对其进行从小到大排序，挑选出个最小的K个位序号构成信息位集合A，从而完成了极化码的设计。

针对一个给定的一般信道W，需要选择对应合适的BEC信道来设计相应的极化码。提出一种量化方法用于获得参数ε的最优值，该方法表明原Arikan提出的启发式方法来设定ε取值的方法并不是最优方法。

仿真结果表明，在SC和LSC译码下，基于BEC信道下设计的高维核矩阵极化码，优于GA-DE方法设计的高维核矩阵极化码，也优于同等码长和码率情况下的2×2维核矩阵极化码。