小波分析在管道泄漏信号去噪中的优化研究

曹雪伟，孙首群，宣立明，林鑫，严亮

(上海理工大学 机械工程学院，上海 200093)

近年来，管道运输因其安全性高、污染小、运输量大、易于自动化管理等优点得到快速发展。但是，由于外界破坏因素或管道材料腐蚀等原因，管道易发生泄漏。管道的压力信号变化是泄漏检测和分析泄漏情况的主要依据，但原始信号具有较强的噪声，如何有效地去除噪声是管道泄漏检测和信号处理的关键。

虽然傅里叶传统分析技术和小波分析技术在信号处理方面各有其特点，但在工程应用领域小波分析技术通常更占优势。在信号处理过程中，傅里叶变换不能同时具备时域和频域的信号特征，有一定的局限性。小波变换采用时频分析方法，具有高时频聚集性，广泛应用于信号的滤波和特征提取中。在焊接超声缺陷检测中，迟大钊[1]等利用非线性小波收缩法将小波分析与相关分析相结合，更好地抑制了超声信号的噪声。在铝合金脉冲MIG焊方面，石玗[2]等通过监测电弧声信号，提取电弧声小波分量的归一化能量，分析得出了焊塌前后的能量变化规律。在搅拌摩擦焊监测中，DAS等运用小波变换提取转矩信号特征，收集搅拌摩擦焊的相关质量信息。

本文针对油气管道泄漏信号，根据信号处理的实际数据和相关理论，为管道泄漏信号的处理提供了一种小波分析的最优方法，丰富了小波分析方法在石油化工领域的应用。

1 傅里叶变换与小波变换

1.1 傅里叶变换

1) 傅里叶变换的定义。在L2(R)空间上，给定1个非周期实函数信号f(t)，则函数f(t)的傅里叶变换为[3]

(1)

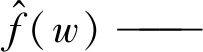
2) 傅里叶变换[3]的基本思想。信号处理时通过对含噪声的信号进行相应的变换，再使用滤波器将噪声频率去除，然后再用逆傅里叶变换恢复信号。

1.2 小波变换

1) 小波变换的定义。假设所给定的非周期实函数信号f(t)是平方可积函数，则式(2)为ψ的小波变换：

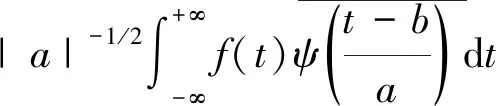
(2)

式中：a——尺度因子；b——平移因子。从式(2)可看出变换前信号是一元函数，而变换后成了二元函数。

2) 小波变换的思想。小波变换[4]的思想是将一元函数信号f(t)等价于多个尺度因子a和平移因子b的小波基函数的叠加和累积。当a和b取不同的值时，可以实现对分析的时间精度和频率精度按需缩放，即在频率变化激烈的部分提高频率精度。

多尺度分析[5]是构造小波分析的理论基础，即通过对含噪信号空间进行分解，然后在分解的子空间里面发掘合适的小波基函数，根据需要从不同的分解角度进行分解，从而实现对原始信号的简单高效的分析和处理。

1.3 傅里叶变换与小波变换的比较

1) 傅里叶变换涉及的函数具有唯一性，包含sinwt, coswt, expiwt三种；而小波分析用到的函数具有多样性，不同的小波函数用在同一个工程问题上产生的结果也不同。

2) 傅里叶变换中w的值与小波分析中尺度a的值大致呈负相关性。

3) 在工程领域的信号去噪过程中，如果采用传统的傅里叶变换分析，去噪效果不太理想，原因在于采用傅里叶变换时的信号处于频率域中，不能给出相应的时域信号特征；而小波分析具有多分辨分析能力，能同时在时域和频率域对信号进行分析，因此能更加有效地、准确地实现信号的去噪。

2 小波去噪方法

2.1 小波去噪方法的分类

假设原始信号为f(t)，被噪声污染后的信号为s(t)，则基本的噪声模型[6]可以表述为

s(t)=f(t)+σ1e(t)

(3)

式中：e(t)——高斯白噪声；σ1——噪声强度系数。为了方便分析，常取σ1=1。从数学观点上分析，噪声模型是以时间为变量的表达式。下面具体介绍小波去噪的三种常用方法。

2.1.1模极大值去噪法

模极大值去噪法[7]主要是利用信号真实值和噪声值奇异点的不同来实现信号的去噪，小波变换能够准确提取信号奇异点的详细信息，从而获取工程上所需的信号特性。

模极大值去噪法是先对函数s(t)实施小波变换，并观察真实信号f(t)和噪声信号e(t)的奇异点随去噪尺度不同而呈现的变化趋势，在区分噪声信号的同时去除噪声带来的奇异点，再依据真实信号对应的奇异点进行小波重构，从而实现去噪的目的。

2.1.2相关性去噪法

相关性去噪法[8]是对含噪信号进行小波分解后，其真实信号的小波系数相邻尺度之间有着某种特殊的关系，而噪声却没有这种相关性，相关性去噪法正是利用该特性去除噪声。

针对离散信号s(n)=f(n)+e(n),n=0, 1, …,M-1进行小波变换：

(4)

式中：Wf(a,b)——小波系数，记作Wa, b；a决定缩放；k决定平移幅度。

由上述分析可知，相关性去噪法是通过比较小波分解每层每个位置上的归一化相关系数的大小，并根据其大小来判断是有用信号还是噪声控制的点。

2.1.3阈值去噪法

阈值去噪法[9]是先按照信号处理的要求对含噪信号进行小波分解，然后对小波系数加工处理，最后对处理后的系数重构，得到原始信号。

阈值去噪法包括软、硬阈值去噪法，两种方法的不同之处主要在于选取的阈值函数不同。典型的阈值估计是Donono等人提出的通用阈值T的估计方法，该估计噪声的方法显示阈值与噪声的方差成正比，尤其是针对时间持续较长的信号，去噪效果会很好，阈值的取值也是根据数学上极大极小化的思想，其阈值函数[10]为

(5)

式中：N——信号长度；σ2——附加噪声的标准偏差。

2.2 小波去噪质量评价指标

小波去噪质量评价指标主要与处理后信号的信噪比和均方根误差两个因素有关。

1) 信噪比SNR。SNR为真实信号能量与噪声信号能量的比值，即：

(6)

式中：Ps，Pe——分别为真实信号和噪声信号的功率，其值可以通过信号采样点的平方和计算得出，去噪质量与SNR大小成正比。

2) 均方根误差MSE：

(7)

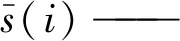
2.3 软阈值与硬阈值信号处理对比

线性信号是所有音波信号中最理想化的一种，考虑选用线性信号进行仿真处理，比较软、硬阈值小波去噪方法对一般信号去噪的效果。由于线性信号中往往连续分布且不含有奇异点，因而只要设置合适的T阈值，对比不同阈值后的信号效果图，便可以较准确地比较软、硬阈值去噪的优劣性。

对比分析的关键步骤是运用相关软件进行信号仿真，模拟1个在[-1， 1]内采样点数为100的线性信号，设置T阈值为0.4，并计算软、硬阈值，得到原始信号、硬阈值信号、软阈值信号的对比，结果如图1所示。

在软、硬阈值信号图1b)和图1c)两图中，小于等于阈值的信号点都转化为零，不同之处在于： 在硬阈值信号图1b)中，大于阈值的信号点保持不变，而在软阈值信号图1c)中，其值大于阈值的信号点转化为该点值与阈值之差。硬阈值去噪法在去噪后的波形上可以看出有非常明显的尖峰，这是由其阈值函数的不连续性造成的后果，然而软阈值去噪法就不存在这样的问题。

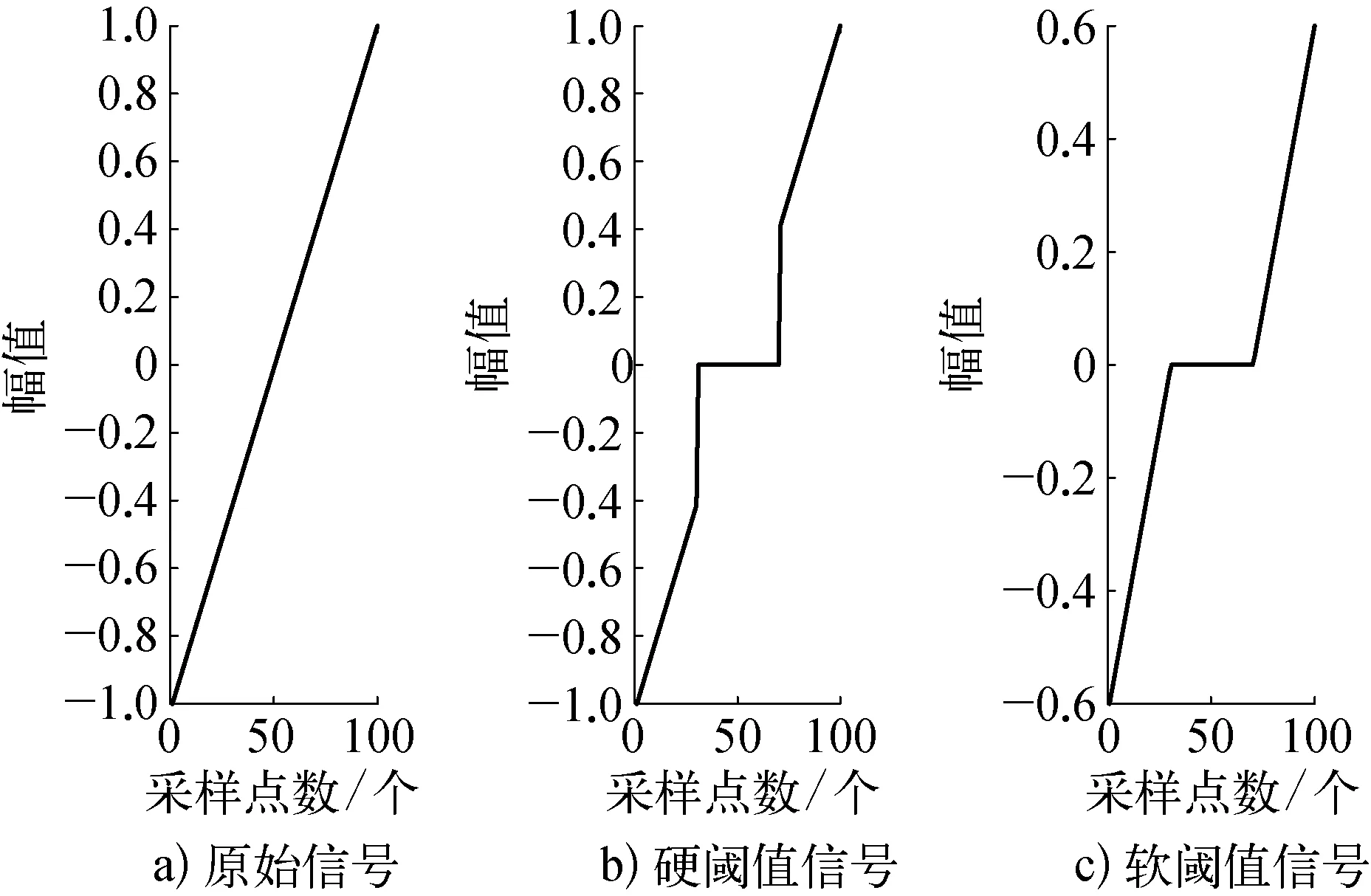
图1 不同阈值下的信号示意

通过以上对比得出，软阈值比硬阈值处理后的信号要更加精准一些，硬阈值法处理信号略显粗糙，故选用软阈值法对油气管道信号进行处理。该步骤的创新点在于： 通过对一般典型信号的处理分析得出软阈值法去噪的优越性，继而应用于特殊油气管道的信号去噪，该方法将普遍与特殊相结合，所得出的小波最优解在实际工程应用领域具有广泛的指导意义。

3 小波去噪案例分析

通过对傅里叶变换与小波变换中软、硬阈值法的二重对比分析，拟选定小波分析在软阈值法去噪的基础上进行信号处理。油气管道因腐蚀穿孔或打孔偷盗等引发管内的输送介质泄漏的同时，往往会伴随着信号的泄漏，在对管道泄漏信号进行小波去噪的过程中，去噪效果受到小波基函数、小波去噪方法及分解尺度3个因素的影响。该研究中确定最优的小波去噪算法是通过逐步寻优分析可以找出最优的去噪算法： 去噪函数最优—方法最优—去噪尺度最优，即通过二重对比与三步寻优相结合的方法可以确定最终的最优小波去噪算法。

3.1 小波基函数的选取标准

小波函数的选取是油气管道泄漏信号去噪处理过程中最重要的一步。常用的小波函数主要包括haar小波、db-N小波、dior-Nr.Nd小波、coif-N小波、sym-N小波。这五种小波函数在实际监测数据分析中的特性见表1所列。

表1 五种小波函数在实际监测数据分析中的特性

鉴于油气管道内信号复杂且数据量大，首先需要采用具有对称性或者近似对称的双正交小波函数，可以使得信号在多尺度分解和重构中边缘尽量不失真；然后应该尽量选用具有紧支撑性质的小波函数，以便工程技术人员准确地获取信号局部特征。

基于以上两点考虑，在综合分析表1的基础之上，选取db-N小波作为油气管道泄漏信号的监测及去噪处理方法。通过分析尺度函数图和小波函数图，并选择相对合适的阶数N进行后续的油气管道信号去噪的实例研究，以下均选定阶数为3， 5， 7进行对比分析不同阶数的db-N尺度函数结果如图2所示。

图2 不同阶数的db-N尺度函数结果示意

由图2可知，在一定范围内，db-N的尺度函数图像随着阶数的增加逐渐趋于光滑，突变点减少；在支撑区间的后部分，其值往往接近零，因而关键区间是函数值较大段。

小波函数在不同阶数下的图像除了平滑度略有提高，但在图形上并没有大幅度的改变，不同阶数的db-N小波函数结果如图3所示。从图2、图3可以看出： 无论是小波函数还是尺度函数，都呈现出一种收敛的趋势，在图形本质上是一致的。考虑到高阶db小波的消失矩较大，计算速度较慢，不太适合运用在管道泄漏信号处理中，故选用低阶的db3小波函数用于油气管道泄漏信号的处理。

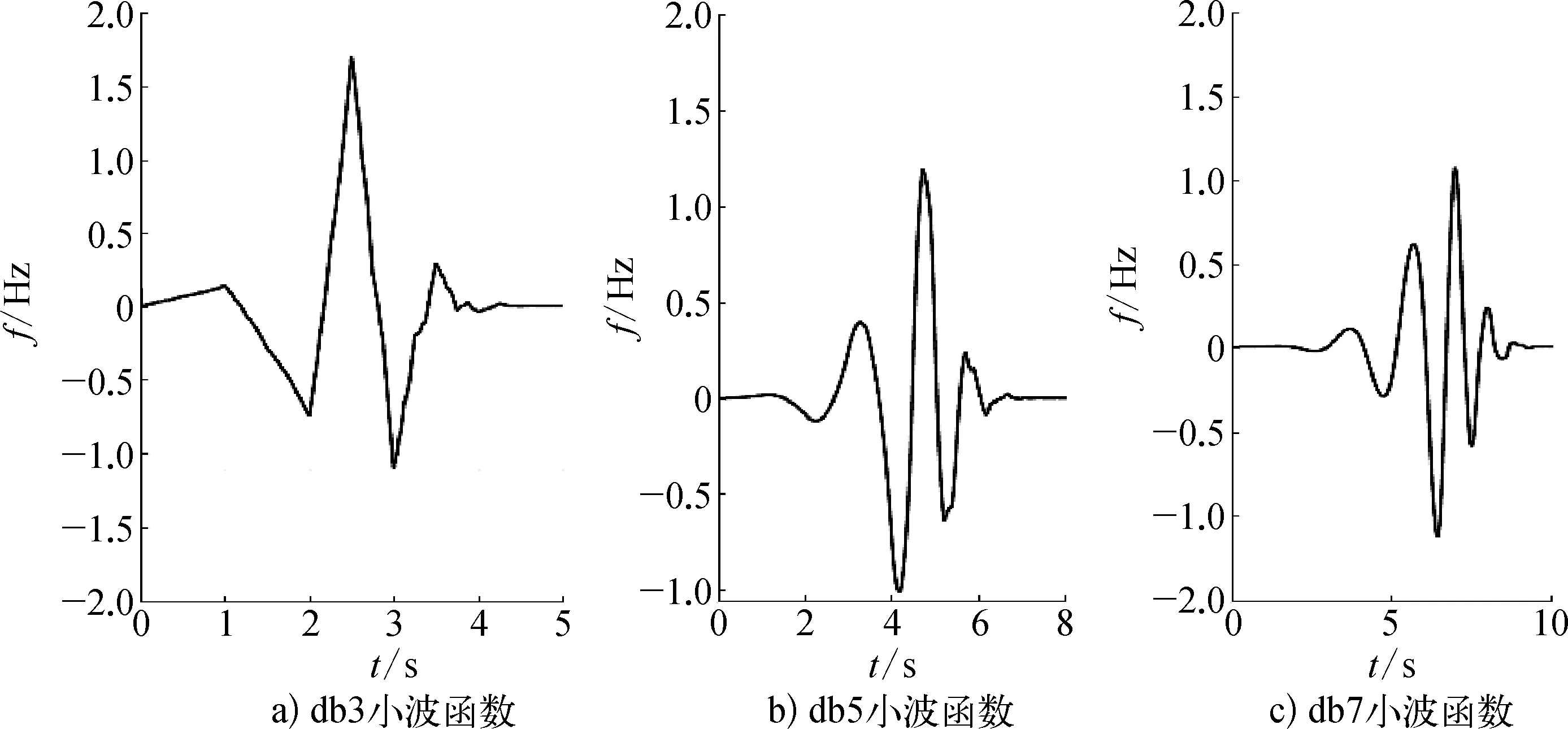
图3 不同阶数的db-N小波函数结果示意

3.2 输气管道仿真泄漏信号模拟

仿真研究的对象是输气管道的泄漏音波，该类音波往往具有非平稳性和随机性，在各类信号中具有普遍性。当管道内部介质发生泄漏时，泄漏音波发生瞬间突变并在一定时间内恢复原样。

该输气管道泄漏信号的仿真模拟是在大气环境为2.5 MPa下进行的，其泄漏位置随机选定在第10 000个采样点处，信号表达式为

(8)

未加噪的原始泄漏信号波形如图4所示，在该波形基础上加入了高斯白噪声的信号波形如图5所示。

3.3 不同去噪方法仿真寻优对比分析

根据软、硬阈值信号去噪效果的对比分析，在两种阈值法去噪法中不考虑硬阈值法，直接选取软阈值去噪与模极大值和相关性去噪法进行寻优分析，为后续的最佳去噪方法的研究提供了便利。根据控制变量的一般原则，将三种去噪法在相同尺度和相同小波函数进行信号去噪仿真，其中阶数为5，均使用db小波函数，不同去噪方法去噪对比如图6所示。

图4 原始泄漏信号示意

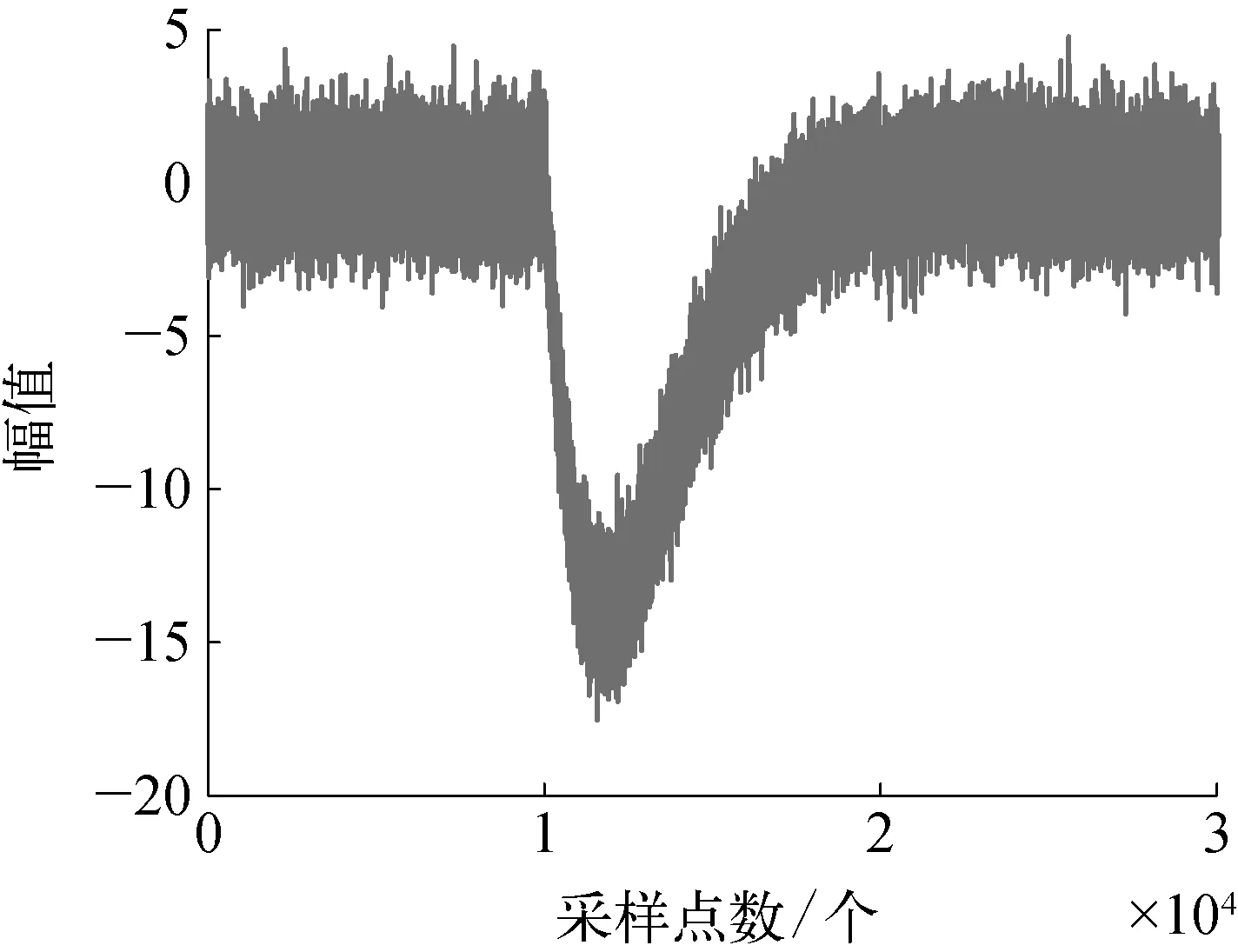
图5 含噪泄漏音波信号示意

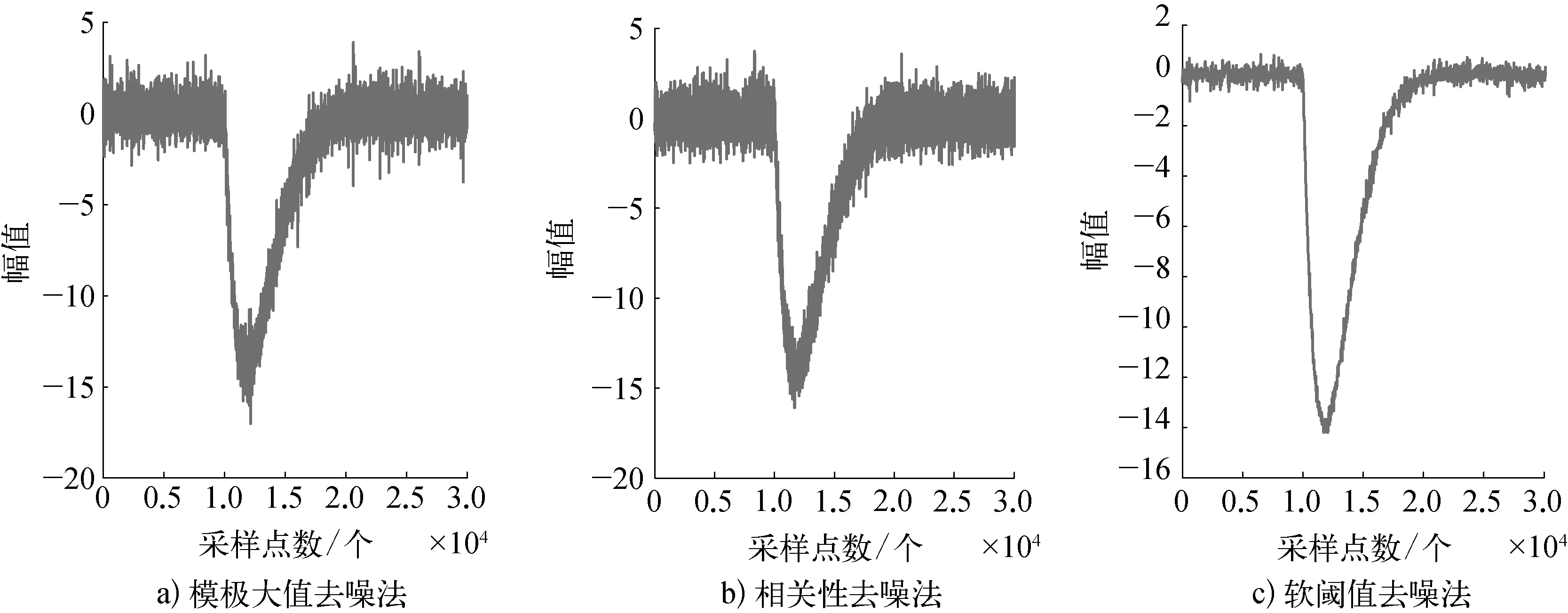
图6 不同去噪方法去噪结果示意

由图6可以直观地看出软阈值法去噪后的图像更加清晰，即实际信号传达的信息更准确，去噪效果更佳。总结上述不同去噪方式的SNR和MSE以及程序运行时间见表2所列。

表2 三种去噪方式对比结果

由表2分析可知，SNR值与信号去噪质量呈正相关性，软阈值法去噪的SNR值最大，而MSE值与信号去噪质量呈负相关性，软阈值法去噪的MSE值正好最小，故该法去噪直接更优。基于以上两点的基础之上，对比仿真去噪运行时间，软阈值法去噪时间最短，因而软阈值法去噪是同等条件下最优的去噪方法。

3.4 不同尺度的去噪方法仿真寻优对比分析

在均选用相同db3小波基函数及软阈值法去噪的前提下，取分解尺度为1～9，对泄漏音波仿真信号进行去噪分析[11]，SNR和MSE结果见表3所列。

表3 1～9种分解尺度去噪结果

根据表3可以直观地看出，当分解尺度为8时，所得到的SNR=81.940 5为最大值，MSE=0.065 2为最小值，根据去噪质量与SNR呈正相关性，与MSE呈负相关性，可知其他条件相同的情况下分解尺度为8时，去噪效果最优，db3小波8层分解尺度去噪结果与未加噪仿真信号对比如图7所示。

图7 db3小波8层分解尺度去噪结果与未加噪仿真信号对比示意

由图7分析可知，由db3小波在8层分解尺度下采用软阈值法去噪滤波后，原始信息得到很好的保留，与原始信息的相似度最高。鉴于油气管道信号处理属于信号整体特性的范畴，应往较大尺度进行考虑。将理论数据与实际情况结合分析，选取8层分解尺度，更加有利于施工人员获取所需信号信息。

4 结束语

针对小波去噪选取原则在工程应用领域尚无理论依据的现实情况，在傅里叶传统去噪方法与小波去噪方法及小波软、硬阈值法去噪的二重对比基础之上，结合管道信号处理的实际数据，通过软件对小波去噪函数、去噪方法及尺度选取进行对比寻优，根据理论分析去噪结果后可得出以下三个结论。

1) 在处理油气管道泄漏信号时，不同小波基函数均可不同程度地去除数据噪声，但最佳小波基的选取需遵循各小波簇系的基本数学特性和小波函数图的变化趋势，两者缺一不可。

2) 通过对管道泄漏信号消噪后SNR与MSE的对比，可以最终得出小波去噪法在选用软阈值法去噪和db3函数的前提下，进行分解尺度为8的去噪方式是最优的。

3) 本文选取2.5 MPa下的泄漏信号以及特定的波形系数作为研究数据，鉴于长期情况下的油气管道会发生弯曲应变和位移，小波去噪方法的选取可能会有局限性，还需在后续的学习中加以研究。