基于半正定测量的光量子OFDM通信系统在离散高斯噪声环境下的性能分析

，

(复旦大学 信息科学与工程学院，上海 200433)

0 引言

量子通信是量子力学与通信技术相结合诞生的一个新兴学科，是量子信息学的重要分支。基于量子力学原理，将微观领域的物理特性加以分析并运用在通信技术上，量子通信具有传统通信无可比拟的优势，是当今世界通信领域的研究热点[1]。然而，现有的量子通信系统通信速率较低，此类量子通信系统所需要的大量光纤资源是无法承受的。如果能在信道中同时传输多个不同波长的光脉冲，采用波分复用技术，就能够很大程度的提升通信速率和信道容量。对于不同波长、频率上独立的光脉冲来说，正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)是契合度相当高的复用方式。目前，来自华中科技大学和电子科技大学的研究团队分别实现了经典全光OFDM在光纤上的传输，分别为8路40 Gbits[2]和8路112 Gbits[3]。对于在全光OFDM系统中的量子态而言，大部分情况下都是非正交的，此时必须采用半正定算符测量POVM(Positive Operator Valued Measure)方法进行检测，可以依据不同的准则设计相应的POVM算符对接收信号量子态进行测量。本文采用了平方根检测SRM(Square Root Measurement)方法[4]，由信号量子态可以快速构造出用于检测的POVM算符，具有较高的研究价值。同时，考虑到实际通信的要求，在接收端，由于量子热噪声的存在，接受态也会变为混合态。虽然高斯量子热噪声的引入会极大地增加问题复杂度，但通过对连续的高斯量子噪声进行离散化近似，则可以在降低复杂度的同时尽可能的逼近实际情况[5]。

本文研究了量子通信的特点，基于马赫岑德干涉仪MZI(Mach-Zehnder Interferometer)的光OFDM系统的通信、不同量子态相位调制对应的SRM检测以及对量子高斯噪声的离散化近似。第二部分介绍了基于MZI的光量子OFDM系统的实现过程。第三部分介绍了量子POVM检测和量子SRM检测方法以及该方法在量子OFDM系统接收端的应用。第四部分介绍了量子高斯噪声对量子态的影响、离散化近似以及检测问题。第五部分研究了基于SRM检测的量子OFDM系统的性能，仿真了加入离散量子高斯噪声后整体的检测错误率并对其进行相应的分析说明。

1 基于MZI的量子OFDM系统

OFDM的主要思想是在频域内将信道分成若干子信道，每个子信道上对一个子载波进行调制，各子载波并行传输。而基于MZI的OFDM系统可以全部在光域上实现，满足量子通信的需求[6]。

在发送端，为保证各个子载波间的频率间隔，由光频梳生成器OCG(Optical Comb Generator)产生8个光子载波，彼此频率间隔相等，在频域上正交。然后利用MZI对于8个正交的光子载波进行量子态的调制。量子信号调制方式是基于MZI的相位调制方式。如图1所示。

图1 量子相位调制器

一个持续时间为T(T=1/Δf,其中Δf是子载波间隔)的光脉冲在发送方处被送入预先设定好相位差的MZI当中，输出的结果是两个持续时间同样为T、非叠加的连续的脉冲，强度各为输入脉冲的1/2，分别用r和s表示，这两个光脉冲，他们之间的相位差Φ表征对应的经典信息，如图2所示。

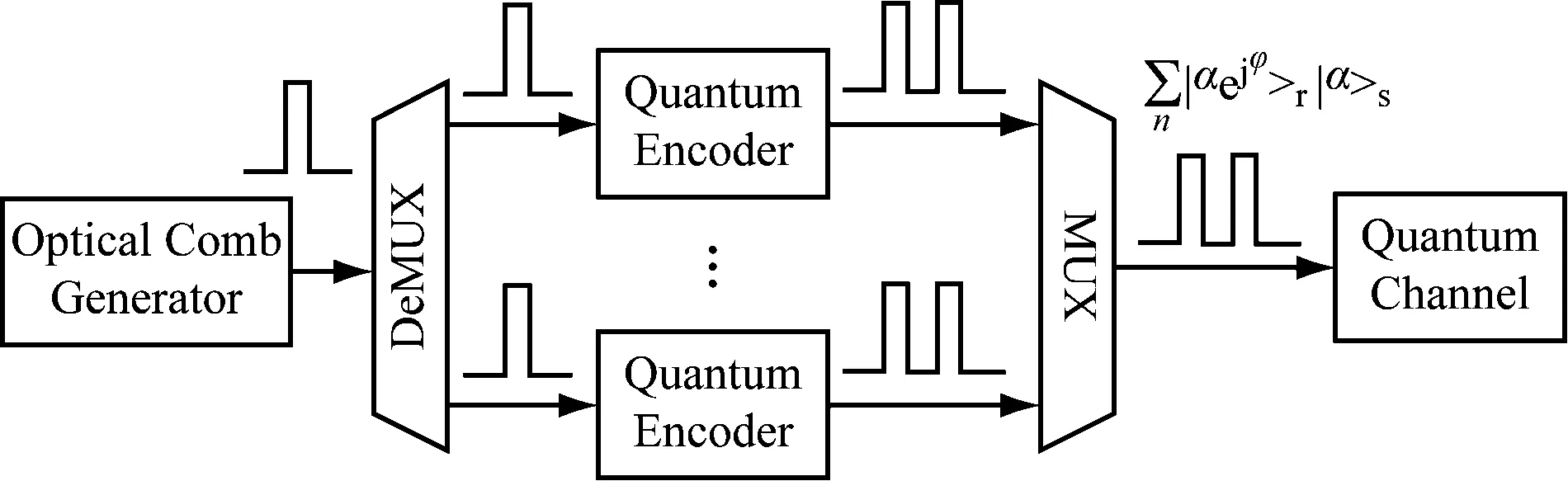
图2 全光量子OFDM系统发射端示意图

在对子载波调制完成后，通过光耦合器将n路光信号耦合为一路，产生携带光量子信息的OFDM符号。

在接收端，接收到的光量子OFDM信号通过一系列级联的MZDI后对各路光子载波解复用，每个MZDI单元由2个耦合器、1个相移器和1段时延线组成。MZDI单元的延时与相移记为(τ,θ)，中心频率为f，则其对应的传输函数可以记为式(1)。

(1)

光量子OFDM信号进入接收端后，每一级MZDI将对其进行延时和相移，经过3级MZDI延时后，光量子OFDM信号的8路光子载波被分离出来，如图3所示。

图3 全光量子OFDM系统接收端示意图(8路光脉冲子载波)

得到不同光子载波上的脉冲r和s后，使其通过预设好的MZI，通过检测门得到相位差同为Φ的位于3个脉冲中间位置的光脉冲，辅以相应的检测，从而得到量子信号当中的经典信息，如图4所示。

图4 量子相位解调器

由于信息调制是在两个光脉冲相对相位上完成的，因此初始的光脉冲相位可以是任意的。同时，在系统传输的过程当中，由于采用了相对相位搭载信息，可能的相位影响会同时作用于两个脉冲，并不会影响二者的相位差，使得系统对于相位噪声有较强的抵抗能力。

2 量子相干态检测

2.1 量子相干态

量子态有许多种形式，其中，相干态是指完全相干的量子光场，也是现实中最容易获得的量子态。在光频领域，电磁场借助于微观粒子体系，通过经典源驱动，通过量子谐振产生相干态光场。因此，由激光器产生的激光就是相干态。相干态是非Hermitian算符的本征态，所以利用相干态集可以构成非正交、超完备的表象。而在光量子OFDM系统中，以QPSK经典信息向量子态的映射为例，可以直观地看到，得到的相干态是非正交的，即式(2)。

k=1,3,5,7,m=1,3,5,7

(2)

显然，当k≠m，即两个相干态的本征值不同时，上式的值不等于0，即两个相干态是非正交的。相干态的光子数态(Fock态)表象形式为式(3)。

(3)

2.2 最小平方根检测

由于光量子OFDM系统中传输的量子态是相干态，而对应不同本征值的两个不同的相干态是非正交的，因而不能通过诸如冯·诺依曼测量等基于完全正交的方法完全确定发送的量子态。因此，需要找到一组测量基，来最小化检测非正交态的错误概率。量子平方根检测是POVM检测中效果较好的一种，是在最小平方根条件下的最优检测。同时，也是当量子态集是由某种几何对称特性的量子态组成的系统中最优的方法。SRM方法的测量基构建十分简洁，可以直接由给定的量子态集合得到。对发送的量子态集合{|αejφi〉}在光子数态表象下(维度为n)展开，得到集合{|φi〉}，它处于n维Hilbert空间中，向量|φi〉是线性独立的，并由所有向量|φi〉构成矩阵Φ=[|φ1〉,…,|φn〉]，它是一个秩为r的n×K的矩阵。对矩阵Φ作奇异值分解，即Φ=U∑V*。记SRM测量矩阵为M，则有式(4)。

(4)

此时，对应的SRM测量是正交测量且满足最优最小二乘测量准则。

取矩阵M的列向量，记为{|μi〉}，这就是最优的测量态集。针对SRM检测方法，对于包含K个发射量子态的符号集系统，在输入量子态等概率的条件下，检测的误码率为[7]式(5)。

(5)

3 量子热噪声的引入

3.1 离散高斯噪声模型

由于量子热噪声的引入，会使得接收端的量子态不再是纯态而变为混合态，考虑对引入量子热噪声的相干态其进行近似。将积分转换为无穷项和的形式表示，即将引入量子热噪声后的相干态视为一个有限数量的相干态的加权和，每个相干态出现的概率则有它所代表的区域Ajk的高斯权重决定。每一个特定的量子态对应复平面上一个特定的区域，接收到它的概率为Pjk是这片区域的权重。这一近似模型称为“离散相干态”近似，即(DCS，discrete coherent state)。

由于高斯分布的性质，当距离更远时，对应的权重会极大地减小，几乎可以忽略不计。因此，以原始信号态为中心，一个单位处分布不同的叠加噪声后的相干态足以相当准确地描述引入量子热噪声之后混合态的情况。

当发射的态为|φ0〉，接受态是[|φ00〉,|φ01〉,…,|φ0k〉],k=0,…,D-1中的任意一个，对应的概率为[P00,P01,…,P0k],k=0,…,D-1。这一系列可能相干态的概率分布则可以由高斯函数在对应区域内的权重得到，对于第k个发射态为式(6)。

(6)

在半径为r圆上对上式积分，即可得到概率为式(7)。

P(r)k=1-e-(r2/N)

(7)

由于噪声的引入，需要重新根据可能的接受态情况构造测量算符。任意一个可能的发射态都有了D个可能的接受态，故整个符号集由之前的K个变为K×D个。相对应的，对于混合态形式的接受态，其POVM算符变为式(8)。

(8)

信号矩阵Φ和测量矩阵M的尺寸均由n×K变为n×(KD)。

3.2 检测错误率分析

上面已经提到，当接收量子态为纯态，针对SRM检测方法，对于包含K个发射量子态的符号集系统，在输入量子态等概率的条件下，检测的误码率由式(X)给出。而对于引入噪声后的检测，量子测量假设依旧适用。假设发射态为Hk，正确检测的概率为式(9)。

(9)

对于包含K个发射量子态的符号集系统，记发射符号对应的先验概率为P(Hk)，正确的检测概率为式(10)。

(10)

由此易知，此时的检测错误率为Pe=1-Pc。

4 系统仿真与分析

为了验证本文中提到的光量子OFDM系统的性能，进行了相关的系统仿真。首先讨论了对量子高斯近似后不同的离散量子态半径范围取值对实际复平面的覆盖情况，然后仿真了引入不同强度的量子高斯噪声对系统检测性能的影响，最后，针对典型的不同的离散量子态半径值在不同强度的量子高斯噪声环境中的情况，进行了整体仿真，并就结果进行了相关讨论。

在用离散相干态模型对引入的量子高斯热噪声进行近似时，近似量子态覆盖区域的半径r是一个较为重要的参数，对r分别取0.4，0.5以及0.6的情况时对整个复平面覆盖比例的仿真结果,如图5所示。

图5 不同近似相干态覆盖半径覆盖率随噪声平均光子数的变化

由仿真结果可以看到，在噪声平均光子数较小，即量子高斯噪声较小时，3种半径取值均能很好的覆盖整个复平面。这是因为，在噪声较小时，叠加了噪声的接受量子态只有很小的概率会出现在离发射的纯态的位置较远的地方。而随着量子高斯噪声的增大，叠加了噪声的接受量子态出现在较远位置处的概率不断增大，此时较小的r覆盖的区域就不能很好的大概率覆盖可能的区域。

接下来我们仿真了在引入维度D=7，不同强度的量子高斯噪声后对系统检测性能的影响，结果如图6所示。

图6 引入不同平均光子数高斯热噪声后系统性能(混合态维度D=5)

由仿真结果可以看到，在采用量子QPSK调制的系统中，对比N=0，即没有任何量子高斯热噪声的情况，即使只引入平均光子数为0.05的量子热噪声，也会对系统的整体性能造成极大的影响。而随着热噪声平均光子数的进一步增加，检测的错误率也会进一步增大。注意到越是在信号态平均光子数较大的时候，有无噪声的存在对系统的影响越大。这是一点可以理解的，因为在信号态平均光子数较大时，同样的比例下叠加了噪声的量子态会偏出更远。

最后，为了综合考虑前文中提到的因素，我们仿真了维度D=7情况下，两种近似量子态覆盖区域的半径r对不同量子热噪声平均光子数的检测性能，如图7所示。

由仿真结果可以看到，在覆盖区域半径r相同的情况下，较小的噪声平均光子数N对应的检测错误率更低，与图7所得的结论相一致。而在其他参数都相同的情况下，较小的量子态覆盖区域的半径的检测正确率更低，因为它对噪声引入的区域覆盖的比例更低，这是可以理解的。但同时也应该意识到，这里的r也并不是取的越大越好，因为当r取的太大，实际上是将很大范围内叠加了噪声的混合态都作为纯态处理，这样也就失去了讨论引入量子热噪声的实际意义。

图7 不同近似相干态覆盖半径下量子高斯热噪声对系统的性能影响(混合态维度D=7)

5 总结

本文研究了量子通信的原理特点以及基于马赫岑德干涉仪的全光OFDM系统，结合量子相位调制的方法，研究并分析了基于马赫岑德干涉仪的光量子相位调制OFDM通信系统。针对光量子OFDM相位调制发送量子态符号集不正交的特点，将发送量子态符号集在光子数态表象下展开，并采用了最小平方根的量子测量方法。并且引入离散量子高斯热噪声近似这一噪声模型，并通过仿真讨论了量子热噪声的引入及诸如混合态维度、近似范围、噪声平均光子数等不同噪声参数对系统所造成的影响及原因。