球形储罐考虑储液晃动时的简化动力学模型基本理论
吕 远, 孙建刚, 孙宗光, 崔利富, 王 振
(1.大连海事大学 道路与桥梁工程研究所,辽宁 大连 116026;2.大连民族大学 土木工程学院,辽宁 大连 116650)
球形储罐是石油化工领域非常重要的存储设备,其存储介质往往为生产过程中易燃易爆的原料、过程料和成品。此类结构一旦遭遇强震,可能发生储罐容器坠落倒塌引起爆炸,进而引发火灾等。因此研究球形储罐在地震作用下的动力响应及抗震、减震措施是很有必要的。《构筑物抗震设计规范》[1]对球形储罐的抗震设计做出了相应规定,其忽略储液晃动效应,采用等效附加质量法将球罐简化为一个单质点体系进行抗震设计,但在地震动作用下球罐的振动为罐内储液与罐壁及支承结构的液固藕联振动,其受力过程较为复杂。事实上,有关储罐类的液固耦合振动国内外学者已经进行了大量研究,但主要针对立式圆筒形储罐,而对举架式球形储罐的研究相对较少。20世纪,学者们对球形储罐的晃动问题进行了理论和实验研究[1-7]。Ramaneyulu等[8]采用有限元数值仿真手段,对LPG球形储罐进行了地震荷载作用下的可靠性评估。Papaspyrou等[9]采用速度势理论针对50%储液球形储罐,推导出了一种用于计算储液动液压力等储液晃动效应的数学解析模型,并研究了不同外部激励条件时的储液晃动效应。Lazaros等[10-11]采用速度势理论推导出了球形储罐和水平圆柱形储罐线性晃动效应的数学模型,并以50%储液时为例进行了地震动响应研究。肖志刚[12]利用有限元软件对球形储罐进行了考虑储液晃动的地震动响应研究,认为罐内储液的晃动吸收了部分地震能量,有利于球罐结构安全。戴鸿哲等[13]采用有限元数值模拟手段,对液化石油球罐进行了地震响应研究,并分析了储液晃动对球罐受力的影响,认为球罐罐体在地震作用下是偏于安全的,其支承体系才是薄弱点。Seyyed等[14]采用线性势流体理论及Mehler-Fock变换求解球罐储液晃动问题,并研究了不同储液高度对动液压力的影响。
目前球形储罐考虑储液晃动的地震动响应研究已经取得了一些成果,但仍处于理论与实验的研究阶段,且理论求解过程十分复杂,不便于工程应用。因此为了更加真实地反应球形储罐在地震动作用时的液固藕联振动动力响应,本文采用速度势刚性理论,根据边界条件推导出合理的势函数,并进一步推导出球形储罐在地震动作用时的动液压力、储液晃动波高、支承底部剪力及倾覆弯矩表达式,构建了便于工程应用的球形储罐考虑储液晃动简化动力学模型,进行了地震动响应研究并与有限元数值仿真模拟计算结果进行对比,辅证了理论推导的准确性。
1 基本理论
1.1 基本假定
由于球形储罐相对于大型立式储罐来说体积较小,但壁厚较厚,且由于其球形形状及主要存储轻质油,所以在液体的晃动过程中罐壁发生的变形极其小,对工程应用来说达到了可忽略不计的程度。故将其假设为刚性罐壁,设x0是球罐罐体在地震动作用时的相对位移,其是时间相关变量,同时我们也知道在由于球罐支承的存在,罐体各部位的位移未必相同,因此x0也是空间相关变量,记作x0(R,θ,β,t)。球形储罐在地震动作用中主要激发第一阶振型,故主要以第一阶振型作为研究对象,现利用有限元软件,对球形储罐进行模态分析,研究其第一阶振型的振动形态。取某一工程实例,建立有限元数值仿真模型,并进行模态分析。
由图1可知,对球罐罐体来说,第一阶振型可近似分解为球罐罐体水平平动及罐体绕赤道面的旋转,由于球罐支承系统的抗弯刚度比抗剪刚度大得多,属于剪切型结构,故第一阶振型以水平平动为主,转动十分微弱,在工程计算时为简化计算可忽略转动影响。Lazaros等在进行储液晃动效应对工业球罐抗震设计影响的研究时便做过类似假定,其忽略了罐体转动影响,假设球罐罐体整体平动,在地震动作用时罐体各部位位移仅为时间相关变量,记作x0(t)。

(a) 第一阶振型
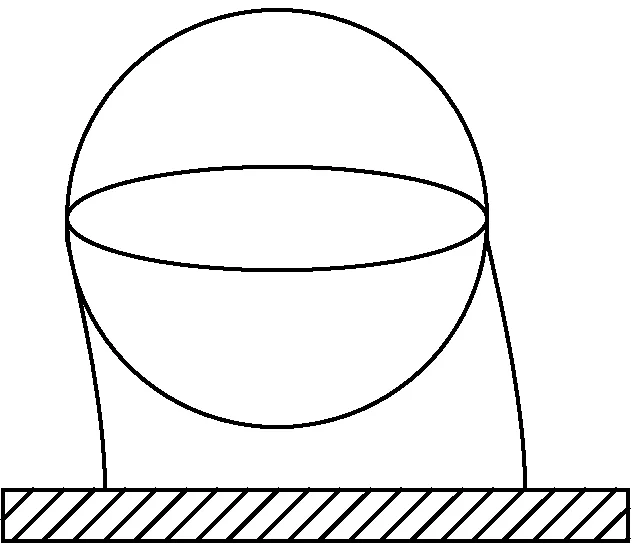
(b) 罐体水平平动
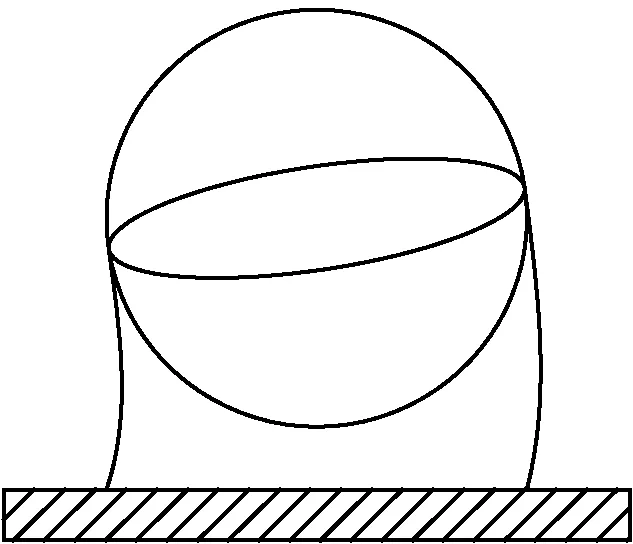
(c) 罐体转动图1 球罐第一阶振型Fig.1 Spherical tank first order mode
同时假定储液为无旋、无粘、不可压缩的理想流体。在地震作用下,根据速度势刚性理论[15-16],储液地震动响应可分为对流运动和刚性运动,储液总速度势可分为刚性速度势和对流晃动速度势,记为Φ(r,θ,β,t)=φr(r,θ,β,t)+φs(r,θ,β,t),满足球坐标系下的Laplace方程:
(1)
球罐计算简图如图2所示,地面运动xg(t)作用下,罐体会产生相对位移为x0(t)的振动。因为φr、φs均满足方程(1),故分别讨论刚性速度势和晃动速度势。
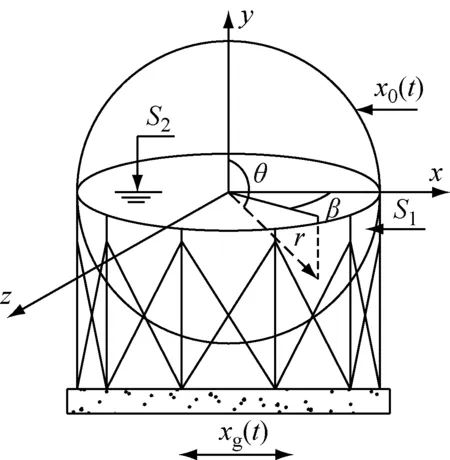
图2 球罐简图Fig.2 Spherical tank diagram
1.2 刚性速度势
根据上述假定,刚性速度势φr(r,θ,β,t)应满足Laplace方程(1)和边界条件:
φr(β+2π)=φr(β)
(2)
(3)
(4)

(5)
1.3 晃动速度势
同刚性速度势,晃动速度势φs(r,θ,β,t)也满足Laplace方程(1)和边界条件:
φs(β+2π)=φs(β)
(6)
(7)
(8)
m=0,1,2,3…
(9)
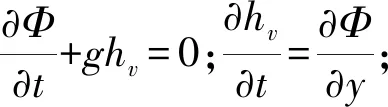
其中hv为表面波动方程,因此可得:

(10)
而又因为x=rsinθcosβ,所以存在
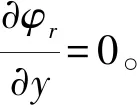
式(10)可以写为:
(11)
将速度势方程式(5)、(9)代入式(11)可得:
(12)
由于式(12)在自由液面S2上均满足,根据叠加原理,可将两边同时乘以调和函数φ*(r,θ),并在圆域S2内积分,所以可以得到如下方程:
sinθφ*(r,θ)rdrdβ=
(13)
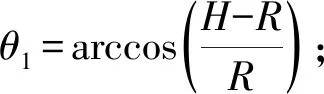
(14)
同时由边界条件(8)可得:
(15)
式(15)在储液与罐壁耦合面S1(r=R)上均满足,同样可根据叠加原理,将两边同时乘以调和函数φ*(r,θ),并在圆域S1内积分,所以可以得到如下方程:
cosθR2sinθdθdβ=0
(16)
将式(14)、(16)相加可得:
(17)
式(17)可以写成矩阵的形式:
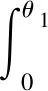
(18)
其中:
(19)
(20)
(21)
(22)
[f]=[fn(t)]m×1
(23)
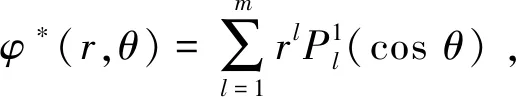
(24)
其中
[M]m×m=[P][N1]T
(25)
[K]m×m=[P]([N2]T-[N3]T+[N4]T)
(26)
(27)

(28)
(29)
(30)
参照结构动力学振型叠加原理[18],可以将式(24)看作是耦合在一起的m阶线性无阻尼运动控制方程,现在需要对其进行解耦,首先求出各阶振型及对应晃动频率:
(31)
式中:ωn为n阶晃动频率,{ψn}为对应的n阶晃动振型;根据上述内容可知,式(24)为m阶矩阵方程,其中m=1,2,3,4,为截断数,其取值不同时结果精度会产生差异;
因此式(24)可以转化为m个非耦合的方程:
(32)
其中
(33)
可将式(32)写为如下形式:
(34)
其中
(35)
式(34)为晃动分量无阻尼运动方程,有阻尼运动方程如下所示:
(36)
由于储液晃动主要以第一阶振型为主,所以只以i=1时为主要研究对象,记xc1(t)=xc(t)。
根据式(32)~(35)可得储液晃动速度势为:
(37)
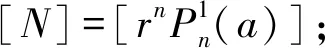
所以总速度势为:
(38)
有了总速度势,可得得出重力场作用下自由液面的振动形态,及储液作用在罐壁上的动液压力:
(39)
(40)
将式(38)分别代入式(39)、(40)中可得:
(41)
(42)
则由储液运动产生的水平方向基底剪力为:
(43)
可以写为:
(44)
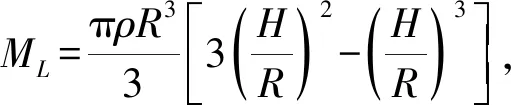
由储液惯性力而产生的对支柱底部的倾覆弯矩也是球罐地震动响应研究时的主要研究对象:
M1(t)=
(45)
其中:
(46)
(47)
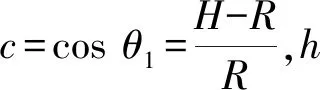

(a) e值

(b) 晃动分量系数
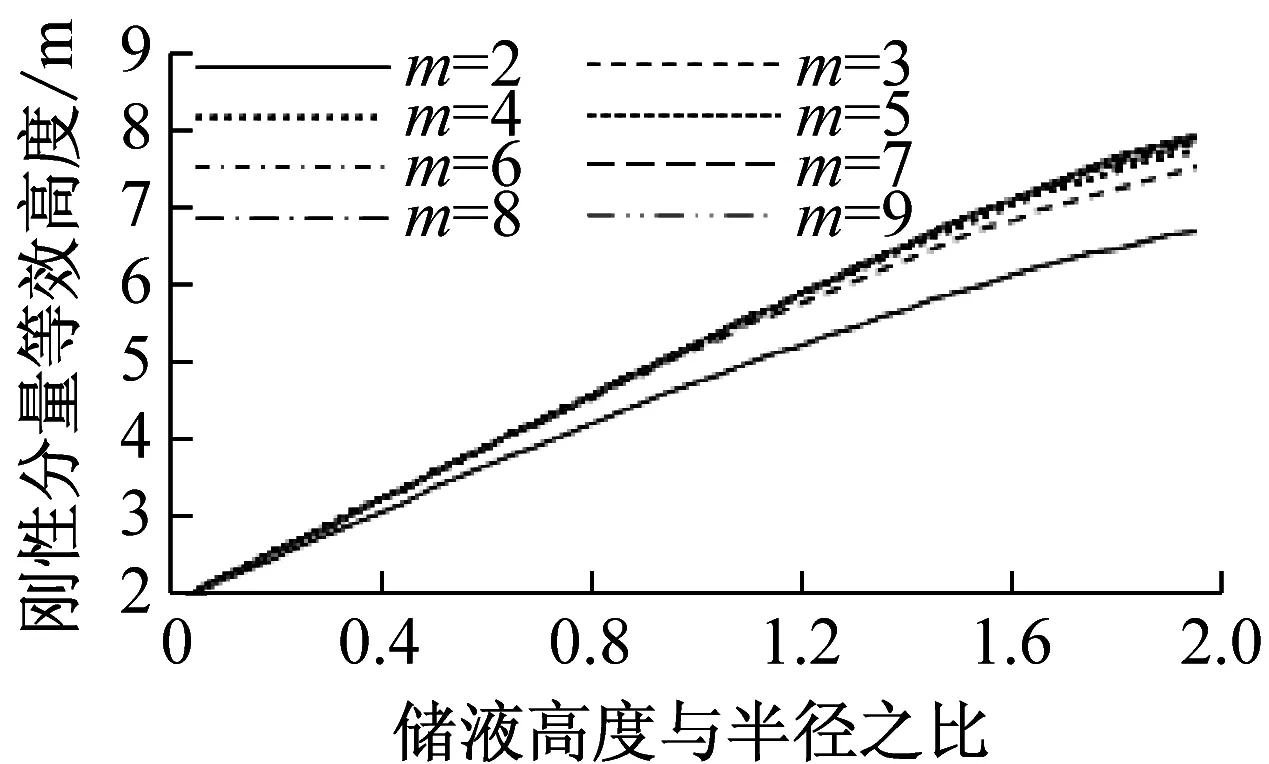
(c) 刚性分量等效高度

(d) 晃动分量等效高度
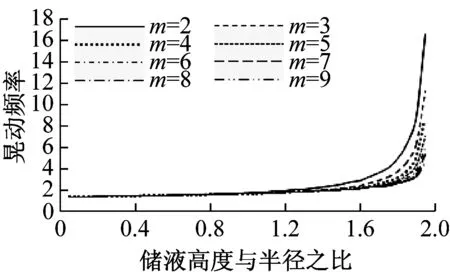
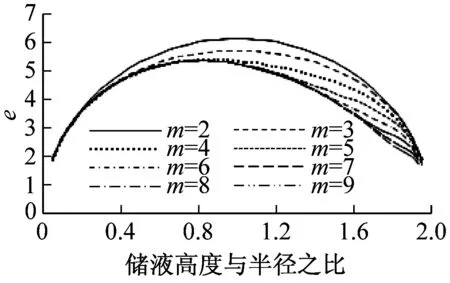
(e) 晃动频率图3 不同截断数m时各参数曲线Fig.3 The parameters curve of different truncated
由图3可知,随着截断数m的增大,各参数曲线趋近于某一值。当m≥8时各参数数值变化已十分微弱,基本满足计算精度要求,因此取截断数m=9。由于上述各参数也受储罐半径R的影响,因此研究不同储罐半径时,各参数的变化情况,计算结果如图4所示。
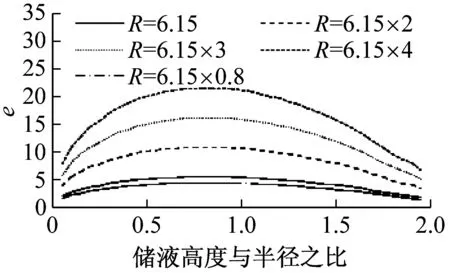
(a) e值
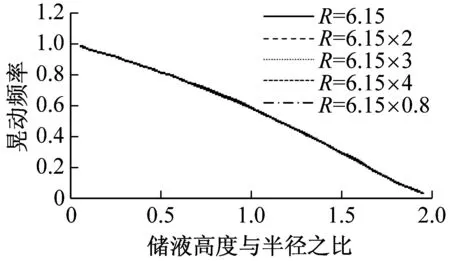
(b) 晃动分量系数
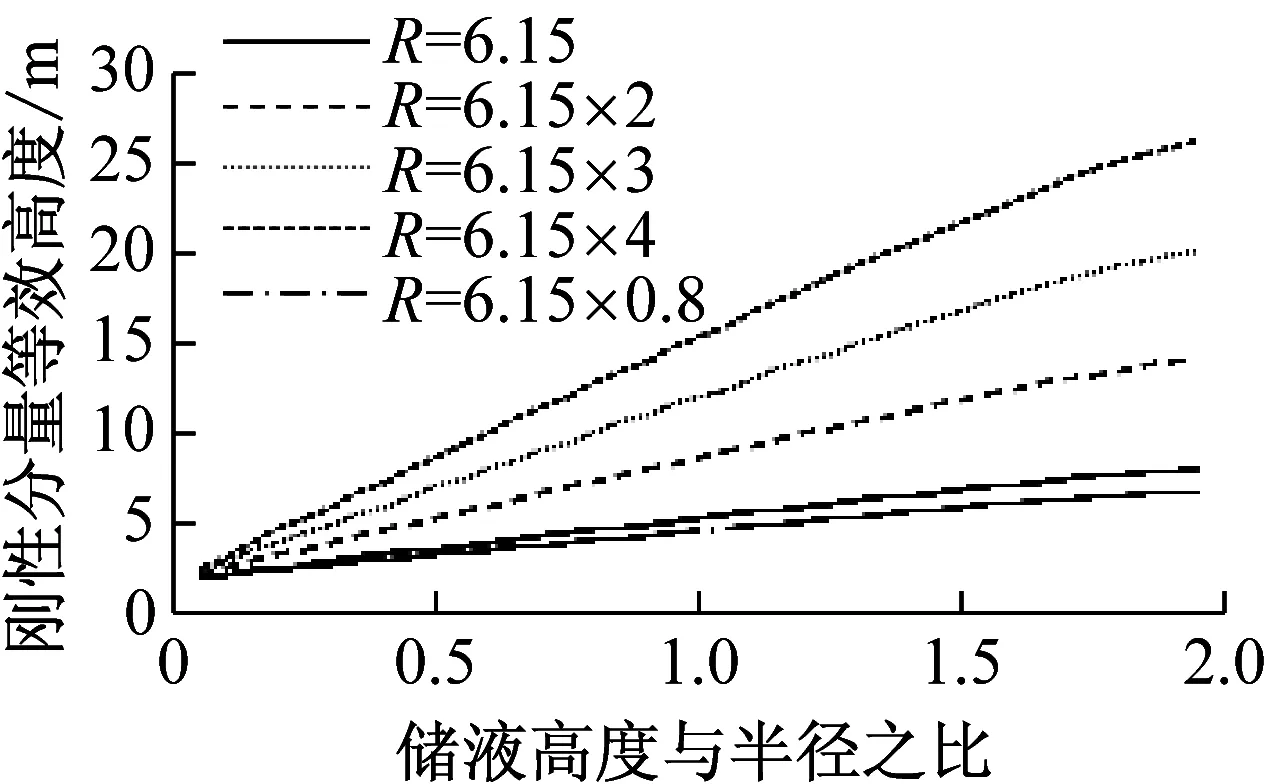
(c) 刚性分量等效高度

(d) 晃动分量等效高度
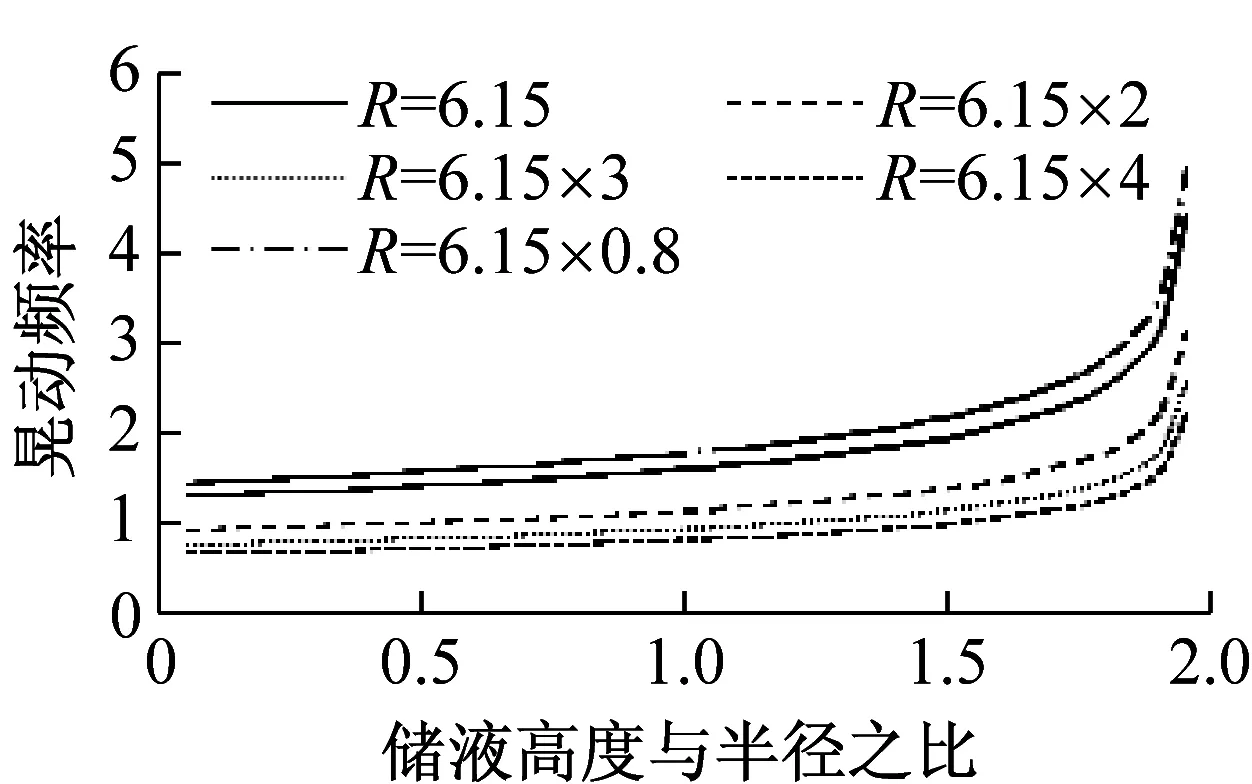
(e) 晃动频率图4 不同储液高度时各参数曲线Fig.4 The parameters curve of different height of the fluid

(48)
s=0.517 9+0.538 1cos(1.377x)-0.072 68sin(1.377x)-0.059 57cos(2.754x)-0.064 12sin(2.754x)
(49)
(50)
hc=(0.035 01x5-0.149 3x4+0.232x3-0.147x2+0.372x-0.002 425)2R+h
(51)
h0=(-0.013 76x5+0.050 26x4-0.066 86x3+0.030 77x2+0.274 8x-0.000 725 7)2R+h
(52)

表1 曲线拟合优度R2Tab.1 Goodness of fit of curves R2
将本文推导的晃动分量系数与晃动频率近似解析解与Lazaros[11]值作对比,如图5所示,发现两者十分接近,由此也辅证了本文推导过程的正确性。

(a) 晃动分量系数对比

(b) 晃动频率对比图5 数值对比Fig.5 Numerical comparison
2 简化力学模型
上述推导中所求出的Q1,M1分别为储液在地震动作用下而产生的作用于支承底部的剪力和弯矩。地震作用时,支柱底部总剪力和总弯矩还应包含由球罐罐体、支承质量、球罐配件等产生的剪力和弯矩。《构筑物抗震设计规范》(GB 50191—2012)[1]中将球罐简化为一个单质量体系:
meq=m1+m2+0.5m3+m4+m5
(53)
式中:m1为球壳质量;m2为液体有效质量;m3为支柱和拉杆质量;m4为保温层质量;m5为球罐其他附件质量,包括各开口,喷淋装置,梯子和平台等。
由于m4、m5一般附加于罐体,1/2支柱和拉杆质量集中于支承顶部附加在罐体上,为便于工程设计,此时也可将m1、0.5m3、m4、m5整合为一个集中质量,记作
ms=m1+0.5m3+m4+m5
(54)
可设地震动作用时集中质量ms对应的相对位移为罐体相对位移x0(t)。
进而可得由于其惯性作用而产生的基底剪力为:
(55)
总基底剪力为:
(56)
由罐体,支承体系及附件等产生的基底弯矩表达式为:
(57)
式中:h1为球壳集中质量等效高度;h3为支承质量等效高度;h4为保温层质量等效高度;h5…hn为各附件等效高度,根据不同球罐结构形式,表示多种附件对应的等效高度。
对球壳来说其对支柱底部产生的弯矩可表达为
m1h1=
(58)
求解积分,可得:
(59)
式中:R1为球罐内壁半径;R2为球罐外壁半径;ρ1为罐体密度;R1-R2为球罐罐壁厚度,相对于R1、R2来说十分小,因此式(59)可以写为:
(60)

(61)
总基底弯矩为:
(62)
则根据式(56)、(62)可以构建球形储罐考虑储液晃动时的简化动力学模型
图6中kc,cc,k0,c0,ms分别为:
kc=mcω2,cc=2ξωmc
(63)
式中:k0,c0分别为支承结构的刚度和阻尼,可根据规范[1]相关公式可得出;ms为储罐和支承结构质量,其等效高度为h+R。由Hamilton原理,可推导相应的运动方程:

图6 球罐简化力学模型Fig.6 Spherical tank simplified mechanical model δ(T-V)dt+δWdt=0
(64)
式中:T,V分别为系统的动能和势能;W为非保守力做的功。
由式(64)可得运动方程为:
(65)
3 算例分析
选取某一1 000 m3液化石油气罐作为算例,储液高度为H=1.5R,忽略其内压影响,储液密度为480 kg/m3,球罐直径为12.3 m,球心距地面8 m,拉杆上部连接处距地面6 m,球壳与支承体系均采用双线性强化模型,算例参数如表2所示。分别选择四类场地中满足规范[1]的五条天然波和两条人工波对球形储罐简化力学模型和有限元数值仿真模型进行地震动响应对比研究,四种场地波加速度反应谱如图7所示,调整加速度时程曲线峰值为0.2 g,计算结果,如表3~6所示。

表2 模型参数Tab.2 Model parameters
从表3~表6中数据可以看出,对不同场地地震动输入,球罐地震动响应差异较大,从(类场地到Ⅳ类场地,晃动波高、基底剪力及倾覆弯矩均值逐渐增大。变异系数反应了各工况计算数值在同场地不同地震波条件下的离散程度,从表中数据可知,变异系数均较小,说明离散程度较小,选波较为合理。而均值差异率则反应了本文推导的理论解与有限元解的差异大小,从表中可以看出,均值差异率均在10%以下,有限元解与理论解十分接近,且理论解均值均大于有限元解均值,计算结果偏于安全,由此则进一步佐证了本文所构建的简化力学模型的准确性及可靠性。
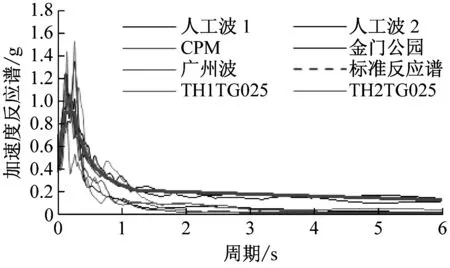
(a) Ⅰ类场地
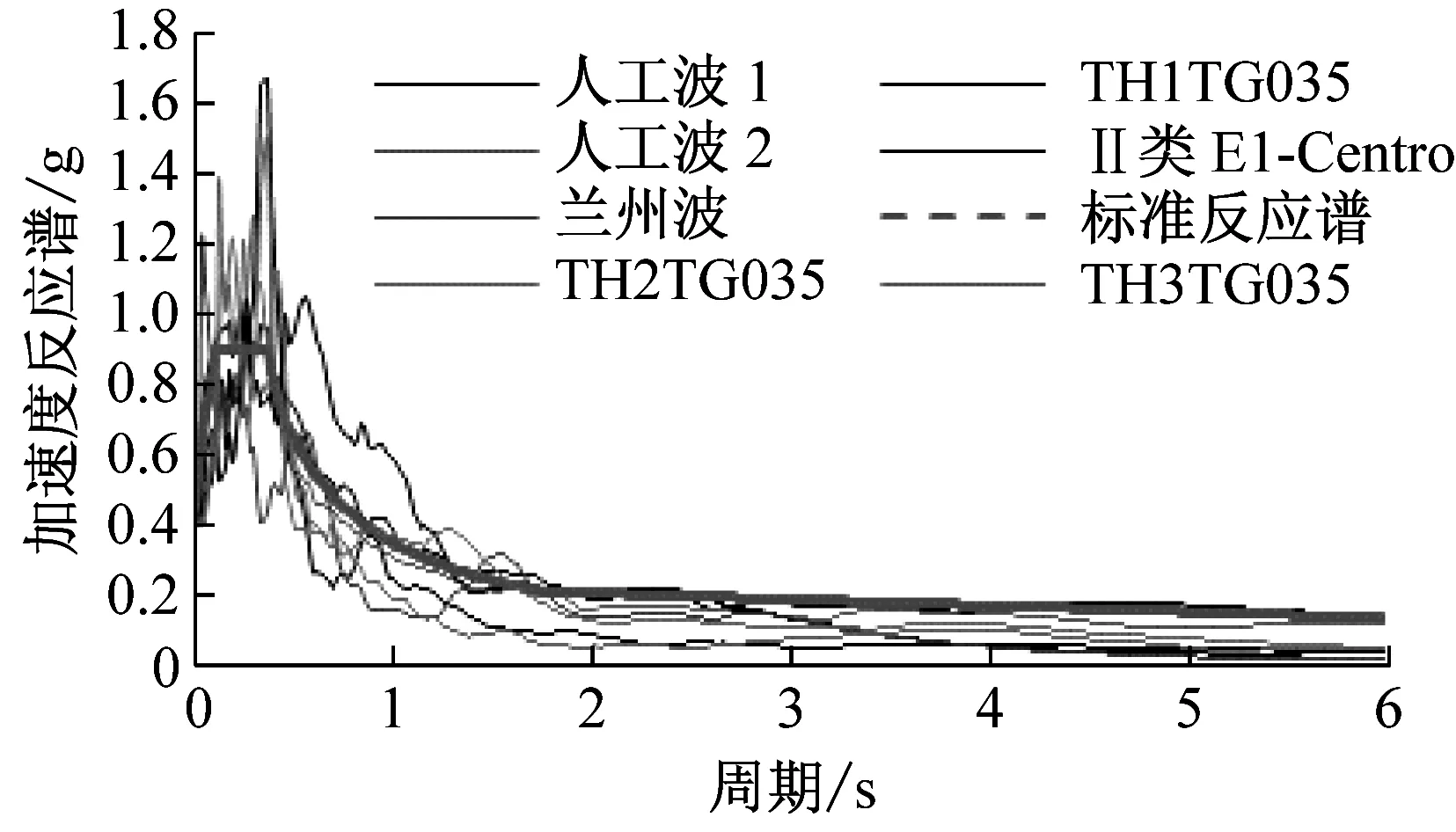
(b) Ⅱ类场地

(c) Ⅲ类场地
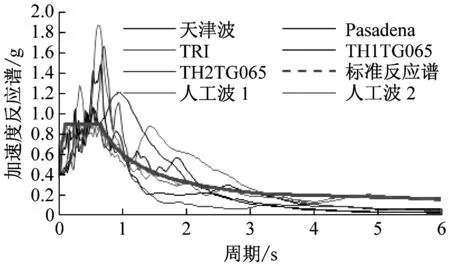
(d) Ⅳ类场地图7 四类场地加速度反应谱Fig.7 Four types of site acceleration response spectrum
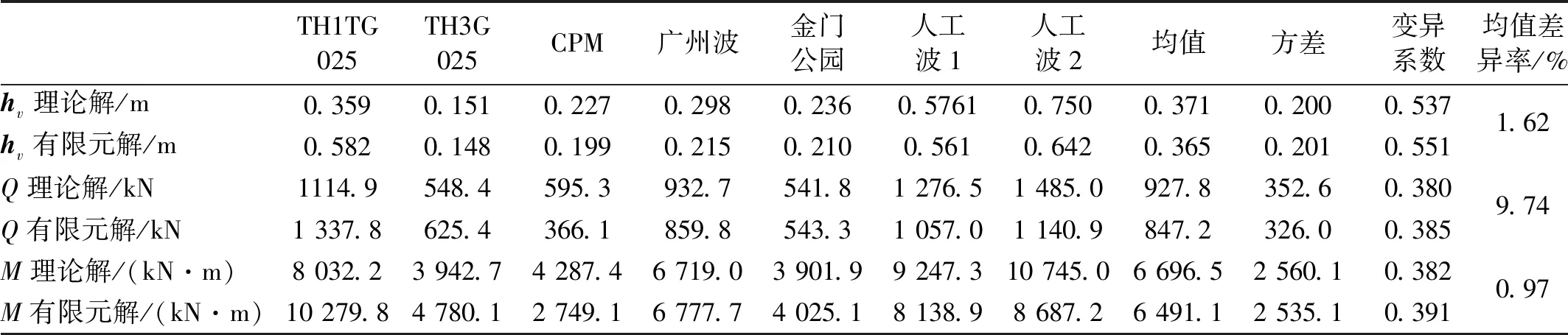
表3 Ⅰ类场地地震动响应对比Tab.3 ClassⅠsite ground motion response comparison
注:差异率=(理论解-有限元解)/理论解

表4 Ⅱ类场地地震动响应对比Tab.4 ClassⅡsite ground motion response comparison
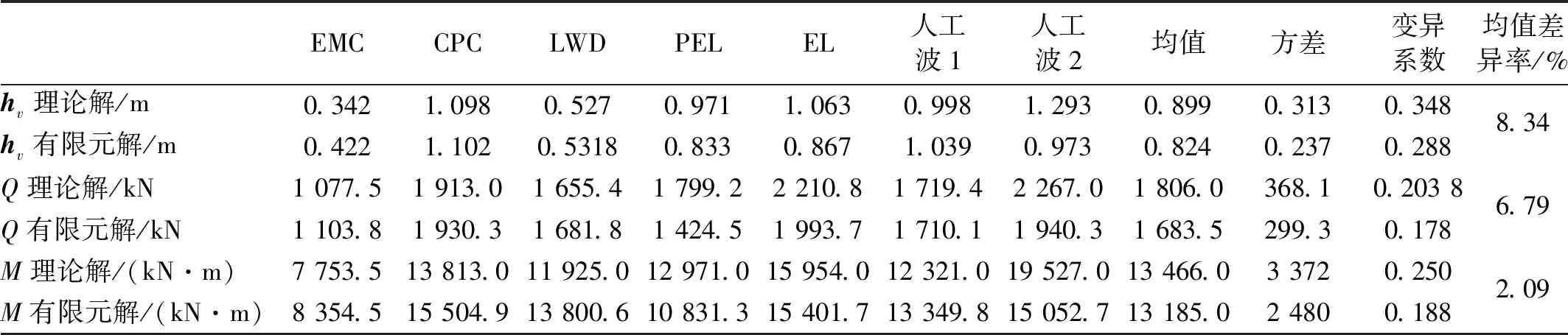
表5 Ⅲ类场地地震动响应对比Tab.5 Class Ⅲ site ground motion response comparison

表6 Ⅳ类场地地震动响应对比Tab.6 Class Ⅳ site ground motion response comparison
4 结 论
(1) 采用速度势刚性理论,根据边界条件推导出合理的势函数,并进一步推导出球形储罐在地震动作用时的动液压力、储液晃动波高、支承底部剪力及倾覆弯矩表达式,并分析了不同截断数m及求球罐半径R对各参量的影响,将本文推导的晃动分量系数和晃动频率近似解析解与与Lazaros值作对比,两者十分接近,由此也辅证了本文推导过程的正确性。
(2) 构建了便于工程应用的球形储罐考虑储液晃动简化动力学模型,进行了地震动响应研究并与有限元数值仿真模拟计算结果进行对比,有限元解与理论解十分接近,且理论解均值均大于有限元解均值,计算结果偏于安全,由此则进一步佐证了本文所构建的简化力学模型的准确性及可靠性。

