中国城镇化碳排放效应的实证检验

牛鸿蕾

（徐州工程学院 管理学院，江苏 徐州 221008）

0 引言

1 研究设计

根据经典经济发展理论，经济发展本身也是一个城镇化、工业化和城乡差距缩小的过程。而据国务院研发中心发布的数据，城镇化率每增加1%，能源消耗量会至少上升6亿吨标准煤。截至2017年底，我国城镇化率已由1990年的26.41%升至58.52%，当年总能耗达3.59亿吨标准煤，在全球位列第一。可见，城镇化进程的加快给节能减排目标的实现带来巨大的压力与挑战。

近些年，涉及城镇化与碳排放关系相关研究的基本情况如下：（1）研究的地理范畴可以是全球多个国家、某个国家或地区、甚至某一省份或城市[1，2]。（2）关于所采用的方法或模型，最常见的是改进STIRPAT模型、库兹涅茨曲线、格兰杰因果关系检验等[3]，此外，还有 LMDI指数模型[4，5]、非参数可加回归模型[6]等。（3）研究结论不尽相同，城镇化率的提升对于碳排放的影响方向问题成为争论的焦点。现有研究尚待补充与完善之处包括：（1）多数研究不专门针对城镇化与碳排放关系，而只是在研究碳排放影响因素时对此有所涉及，难以实现全面而深入的分析；（2）即使是专注于这一问题的研究，多数没能体现出城镇化的碳排放效应在国内各区域间的差异性及关联性，且忽视这一效应可能呈现的动态性与延续性特征。（3）在分析模型中，将城镇化水平简单的等同于城镇化率高低是不够全面的，很可能造成效应评价结果的偏差。

本文基于STIRPAT模型和动态空间面板数据模型，根据2002—2016年省域面板数据，实证分析中国城镇化的碳排放效应。与以往研究的不同主要体现在：采用的模型同时具备空间相关性与动态性特征；除城镇化率以外还纳入新的变量-城市首位度来表示城市规模分布的变化。

1.1 基本模型

19世纪70年代，IPAT模型（I=P×A×T）由Ehrlich和Holden（1971）[7]提出，式中的I、P、A和T分别代表环境效应、人口、人均财富和技术水平。之后，Dietz和Rose（2003）[8]又提出其随机形式即STIRPAT模型（I=aPbAcTde），其中，a为模型的系数，b、c、d为各驱动力指数，e为误差，该模型可转化为：

为测度城镇化对碳排放的影响效应，拓展模型（1）时重点纳入城镇化的相关变量，可得：

式中，S表示产业结构变动指标，UR代表城镇化率水平，US是城市规模分布变量，f、g和h分别指S、UR和US的系数，i和t则分别代表省域和年份。

本文对模型（2）中变量的定义如下页表1所示。另外，有两点需要说明：（1）碳排放总量I是指人类活动引起的碳排放，大约占总排放的90%以上。IPCC中介绍了三种方法测算固定和移动源的石化燃料燃烧碳排放，本文会采用第一种方法：根据燃烧的燃料数量和缺省排放因子来估算二氧化碳排放量。该方法的测算或多或少存在准确性不足的问题，但因其具备简单易行、对数据要求不高的优势，故而被采用。（2）除通常采用的城镇化率变量以外，新增城市规模分布变量，从另一个侧面反映城镇化发展情况，该变量用城市首位度指数US来表示。Jefferson（1939）[9]最先提出城市首位律：首位城市在大多数情况下是一定地理范围内的经济、政治与文化的交汇中心，对于周边城市有巨大的、多方面的影响力。此外，他构建的城市首位度指数—“两城市指数”法能够清晰、明了地概括城镇规模分布情况，故被本文采用。

表1 模型（2）中各变量的定义

1.2 模型构建与变量说明

面板数据模型在社会科学研究领域已得到广泛运用，为添加动态因素，进一步纳入滞后因变量，就构成动态面板数据模型。这类模型既能通过控制固定效应较好地克服变量遗漏，又能较好地解决反向因果性问题。其基本形式如下：

式中，y和x分别代表因变量和自变量，α和β分别是y和x的系数，ui表示未被观察到的定常异质性，εit是特质误差项，假设yi0和xi0是可观测的。i=1，…，N，t=1，…，T，并且满足。与一般面板数据模型类似，动态的面板数据模型也包含两类：当ui待估的是固定参数时，该模型是固定效应模型；若ui是随机的，则为随机效应模型。

J.Paul Elhors（t2003）[10]将动态面板数据模型与空间残差自回归形式相结合，建立一种动态空间误差面板数据模型，如下：

若仅将空间自相关性变量纳入该动态面板数据模型，可得一种动态空间滞后面板数据模型，如下：

模型（4）和模型（5）中，t=1，2，…，T，i和j都代表省份，i=1，2，…，N，j=1，2，…，N，wij为n×n阶的空间权值矩阵W中的某个元素。令模型（4）和模型（5）中xit=[lnPit，lnAit，lnTit，lnSit，lnURit，lnUSit] ，可 得 两 种 实证分析模型。上文已提到ui既可表示固定效应，又可指随机效应。实际上，当样本是随机抽取自考察总体时，随机效应模型更适用，但本文回归分析针对的是中国省级区划单位这些特定个体，采用固定效应模型更为合适。因此，这里ui为固定效应，且存在三种可能的情况：地区固定效应、时间固定效应或时间地区固定效应。那么，分别与模型（4）和模型（5）结合，可构建6种实证模型形式，下文将采取LMerr、LMsar及其稳健形式的统计检验法对其进行初步的筛选。

1.3 空间权重矩阵构建

构建空间权重矩阵的方式大致有基于邻接标准和基于距离标准两类，第一类方法可设置系数为1或0分别来表示两地区相邻与否。依据地理学第一定律，人类行为对所在地区的影响随距离的加大而减弱，仅通过区域间是否相邻将其间关联程度简单定为0和1两种，不太符合客观实际，这一关联程度应是渐变的，故本文采用反距离平方法构建空间权重矩阵W，令其中，d表示第i省与第j省中心位置之间的欧几里德距离，该距离根据国家地理信息系统网站提供的1：400万电子地图，利用Geoda095i软件测得。另外，模型估算时需对W进行行标准化处理，即用各元素除以所在行的行元素之和，可使每行元素之和为1。

1.4 参数估计与数据来源

根据非空间动态面板数据模型的估计思路，J.Paul Elhorst（2005）[11]提出用无条件极大似然法估计线性和对数线性的空间面板数据的动态模型。已被证明的是：当N→∞,t为任意值时，标量a和参数向量β具有相容估计量，并且，ML估计比GMM估计[12]更有效率。故本文采用J.Paul Elhorst提出的无条件极大似然法估计实证模型。为确保数据的可获性、完整性与连续性，本文采用中国29个省级区划2002—2016年的面板数据，港澳台地区、青海和西藏的数据因其资料不够完整未被包括。主要数据来源于由中国统计局出版的相关年份的《中国统计年鉴》、《中国能源统计年鉴》、各省级区划统计年鉴等。

2 实证检验与分析

2.1 空间自相关性检验

为了检验空间自相关性，即观测同一变量在不同空间区域上的相关性，下文借助全局空间自相关指数（Moran's I）来整体描述碳排放的空间分布模式，同时使用空间相关局域指数反映空间要素的异质性，而LISA本质上是将Moran's I分解到各个区域单元的结果，故又称为局部Moran's I。因篇幅限制，上述两种指数的计算公式及推导过程不再赘述，具体参见文献[13] 。

如下页图1所示，Moran's I在2003—2016年间波动不大，基本保持在0.16～0.21之间，显著性水平始终低于5%。具体来说，Moran's I在经历2002—2004年间的显著下降以后开始明显上升，于2008年达到0.2010的最高点，之后又有小幅的回落，但总体上波动不大、较为稳定。可见，各省域的总碳排放整体呈现较强的正相关关系，即碳排放量较高的省域或地区相对的相互邻接，而具有较低碳排放的省域或地区也相对的相互靠近，目前这种空间维度的相关性仍停留在较高水平。

图1 2002—2016年我国省域总能耗碳排放的Moran's I

利用Geoda软件绘制2002—2016各年LISA集聚图（图略），这是一种局域空间自相关分析方法，将各省碳排放量分为四种类型的分布模式：HH（High-High）表示高碳排放区域被同是高碳排放区域包围的空间关联形式，LL（Low-Low）代表低排放区域被低排放区域所包围的类型，LH（Low-High）指低碳排放区域被高碳排放区域所包围的空间关联类型，HL（High-Low）表示高碳排放区域被低碳排放区域所包围。其中，前两种属于正的空间相关性，后两种属于负的空间相关性。根据所得LISA集聚图发现：辽宁、内蒙、河北、江苏、山东、贵州、广西、海南等部分省域碳排放之间存在不容忽视的空间维度异质性与依赖性；另外，尽管在青海、安徽、吉林等少数省域的情况有所变化，但HH、LL、LH和HL各类集聚区的总体分布变化不大。具体来看，大部分具有较高局部Moran's I的热点区（即HH集聚区）分布在江苏、山东、河北、山西、河南、辽宁和内蒙古等地，地理位置较为集中，主要位于中国的北部、东北部和东部，而这些省域及其邻省都产生较大的碳排放。同时，LL集聚的盲点区大部分分布在青海、贵州、广西和海南等省域，因为这些省域及其邻域的碳排放量相对较低。因此，相对其他地域，属于热点区或盲点区的省域在碳排放方面具有较小的空间异质性和较强的正相关性。被热点区包围的省域（如吉林和天津）多数情况下属于LH类型，这类地区的碳排放量要小于其相邻区域。此外，经济发展更快的广东省比其周边地区（包括广西、江西、湖南等省域）产生更多的碳排放，故属于HL集聚区。

2.2 LMerr、LMsar及其稳健形式的统计检验

在固定效应的空间面板数据模型中，截距项能分解为时间固定效应、地区固定效应和时间地区固定效应。假定三种效应均可能分别存在于模型中，从而构成一系列不同形式的模型，为对其进行有效筛选，估算LMerr、LMsar及其稳健形式的统计量，如表2所示。以时间固定效应的面板数据模型为例，LMsar和R-LMsar的统计量分别等于9.0905和8.7528且远大于LMerr和R-LMerr的统计量0.7597和0.4221，这说明当包含时间固定效应时应选择空间滞后面板数据模型形式更贴近研究现实。以此类推，能够将其余两种模型选定为：含地区固定效应的空间滞后面板数据模型和含地区时间固定效应的空间误差面板数据模型。

2.3 模型估计结果分析

不同固定效应的动态空间误差或滞后面板模型的估算结果如表3所示。由R2、σ2和对数似然值（log-likelihood）、各模型估算的变量系数及其显著性水平来看，时间固定效应的动态空间滞后面板数据模型要明显优于其他模型，说明碳排放在我国区域分布具有的阶段性或时间性特征要强于区域性特征，故下列分析均针对这一模型的估计结果。

表2 不同模型的空间依赖性诊断

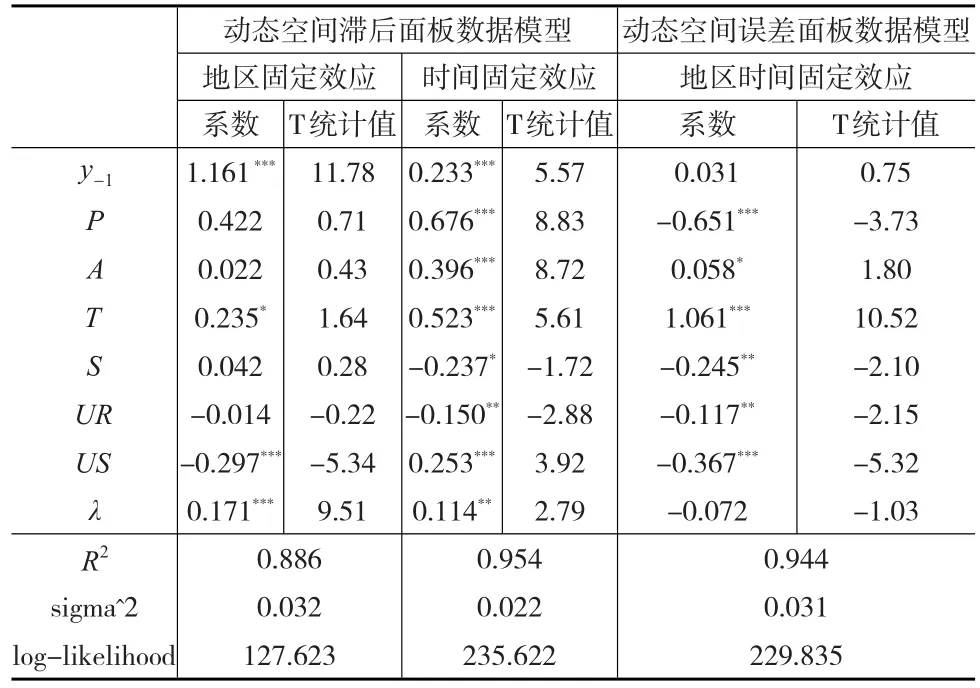
表3 动态空间面板数据实证模型的估计结果

（1）关于滞后因变量

碳排放滞后项的系数是0.233，显著性水平为1%，这表明滞后一期的碳排放增长对当期碳排放有显著的正向影响。由图2可知，除个别年份较上一年稍有下降之外，中国碳排放总量几乎每年都在增长，1996—2016年间由40.9亿吨增至127.1亿吨，年均增速达5.82%，在大多情况下年环比增速接近或超过3%，在2004年和2005年分别达到了16.1%和17.3%的最高值。碳排放量的趋势线所呈现的是一种连续、渐进且稳定的碳排量增长态势。

图2 1996—2016年我国的碳排放量及其增长率

（2）关于空间自相关系数

对于带时间固定效应的动态空间滞后面板模型，空间自回归系数λ的估计值等于0.114，显著性水平为5%。这说明，周边地区碳排放的变化会导致本地区碳排放的同向变化，可见，加大对于某些省域的碳排放控制与治理，所产生的降碳效应会在一定程度上扩散到周边地区，在制定相关方针政策时应充分考虑到省域间碳排放的联动性，有效发挥省级政府环境规制在节能减排领域正面的外溢性。

（3）关于自变量城镇化率

自变量城镇化率的估计系数是-0.150，显著性水平为5%，说明城镇化率水平的提高显著抑制了碳排放增长。然而，这仅表示一种整体效应，并不意味着盲目提升城镇化率就能直接带来碳排放的下降。因为城镇化进程本身是一个涉及多个领域的复杂系统工程，而城镇化率只是从城市人口角度出发来衡量城镇化水平的一种指标，并不能全面反映城镇化进展情况，例如发展质量。实际上，很多与城镇化相关的因素会对碳排放产生直接或间接的不同方向影响，这些影响力相互抵消或者增强，最终形成总体的碳排放效应并通过统计分析结果显现出来。总之，真正影响碳排放的是城镇化发展方式而非城镇人口增加本身。

图31978 —2016年我国城镇化率

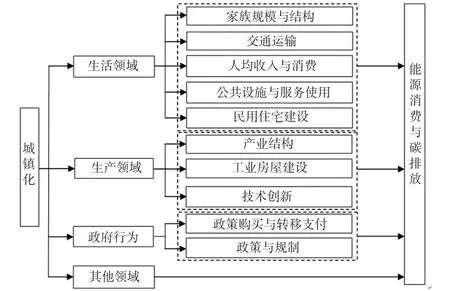
图4 城镇化的碳排放效应的概念框架

如图3所示，城镇化率在1978年只有17.9%，1995以来进入加速增长期，于2016年达到历史最高点57.4%，而期间的增长趋势一直非常稳定。由图4可知，城镇化的发展会给生产、生活、政府行为等不同领域所涉及的诸多方面带来一系列的改变，而总体效应的正负取决于不同方向影响力的合并结果。根据生态现代化理论，在某些阶段城镇化与碳排放可能正相关也可能负相关，这取决于城镇化的相关因素对碳排放不同作用力的合并结果，具体分析如下：

第一，在中国城镇化和老龄化的背景下，家庭规模小型化和家庭形态的多样化趋势越来越明显。家庭规模通常被作为决定家庭碳排放量的一个重要因素，因为较大的家庭规模往往带来规模经济效益[14]。

第二，城镇化会影响相关产业的发展和产业结构调整。居民从农村到城镇的迁移会推动工业化进程，随着工业吸纳就业的增加，农业就业人数所占比重由1996年的50.5%降至2016年的27.7%。一方面，农业生产运营的机械化带来对人工需求的减少，而现代工业和制造业的劳动密集程度在减弱，单位能耗也在减少。另一方面，城镇规模的扩大与数量的增加，在一定程度上推动了第三产业发展，而该产业已经并将继续在节能工作中发挥日益重要的作用。

第三，在城镇化进程中，越来越多的居民聚居于高层建筑、利用公共交通、选择能源密集程度低的交通运输方式，借助由此带来的规模经济优势，很多城镇对于能源的消耗有所减少。

第四，城镇化有助于要素集聚，增加城镇和农村居民的工资，改善他们的生活水平，进而带来更多的能源消耗。尤其是随着城镇服务业的扩张，城镇居民会有更多的工作机会和更高的工资，而农村剩余劳动力向城镇的转移也推动农产品市场的发展。

第五，为满足城镇化加速期的时代要求，政府会通过制定和实施环境治理与产业发展相关的政策措施，控制与约束企业与相关部门的高能耗行为，并大力加强技术创新、推广清洁生产与技术、新能源的运用等，从而有助于节能减排目标的实现。

（4）关于自变量城市首位度

自变量城市首位度的估计系数是0.253，显著性水平为1%，说明城市首位度与碳排放是显著正相关的。可见，目前城镇规模扩张的负外部效应居主导，盲目扩大城镇人口规模不利于节能减排。如下页图5所示，从2002—2016年，我国各省域城市首位度的平均水平总体呈现增长态势，说明越来越多的人口集聚在首位城市，该城市的人口规模与其他城市之间的差距越来越明显，而与此同时，碳排放总量维持稳定增长状态，可见，将城镇规模优化控制在一个高能效的合理范围内至关重要。实际上，较大的城市首位度有助于推动技术创新、技术扩散与产业升级等，并降低交易成本、劳动力配置不合理的风险与服务成本等，从而带来碳排放总量的减少。然而，若首位城市人口规模超过其承受范围会带来高额的生活成本、交通拥堵严重等一系列问题，也会拉大小城镇与之在技术与生活服务设施方面的差距，加剧资源分布的失衡，导致小城镇难以有效承接技术扩散、知识溢出与转移，环境恶化、碳排放量增加等一些负外部效应随之显现。

（5）关于其他自变量

变量P、A和T的系数分为0.676、0.396和0.523，显著性水平为1%，S的系数为-0.237，显著性水平均位于10%，这表明我国总人口数、人均国内生产总值和能源强度对于同期碳排放量有较强的正向影响，而变量产业结构（第三产业所占比重）对其的影响方向则相反。

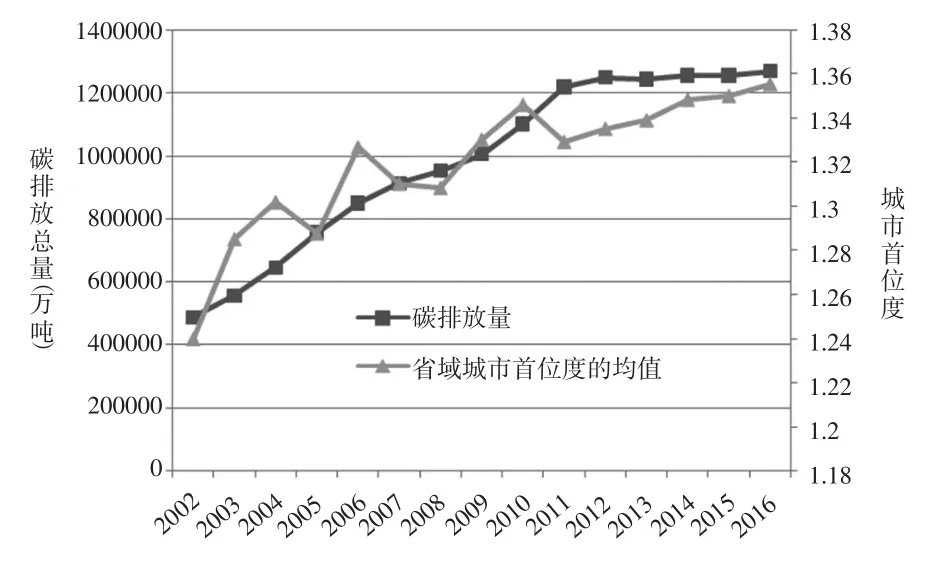
图5 2002—2016年我国碳排放总量及省域城市首位度的均值

3 结论

基于拓展的STIRPAT模型和动态空间面板数据模型，本文实证考察了中国城镇化的碳排放效应。得到结论如下：

（1）我国各省域（或区域）的碳排放存在一定空间维度的依赖性和异质性，周边地区碳排放的变化会导致本地区碳排放的同向变化，而节能减排活动对于当期碳排放的影响力会在将来持续产生作用。这意味着，各级政府在制定相关方针政策时，既要充分考虑到省域间碳排放的联动性，有效发挥政府环境规制在节能减排领域正面的外溢性，并力求各省域与其周边地区协调、互助共建低碳发展体系，又应从长期与短期的不同视角出发，确保降碳效应的延续性与持久性。

（2）随着近些年城镇化率水平的大幅提升，城镇化对碳排放的增长总体呈现出抑制作用，但并不能说明单纯提升城镇化率就可降低碳排放。因为城镇化本身是一个涉及多个领域的复杂系统工程，对于碳排放存在多角度的影响且其方向不尽相同，目前显现出的总效应是各方力量相互强化或抵消的结果。真正影响碳排放的是城镇化的发展方式与实现路径，那么，在城镇化率提升的过程中，应优化城镇化低碳发展模式，大力发挥城镇化的降碳效应，同时尽可能的遏制其增碳效果，充分协调城镇化相关要素间的矛盾与关系以最终达到节能减排总目标。

（3）较大的城市首位度有助于推动技术创新、技术扩散与产业升级，降低交易成本等，但同时加剧资源在大小城镇分布的严重失衡，导致小城镇难以有效承接技术扩散、知识溢出与转移、碳排放量增加等一些负外部效应随之显现。可见，在增加城镇人口比重的同时，应合理控制各城镇人口规模差距，才能确保在城镇化顺利发展的条件下，城镇规模分布变化所带来的环境友好效应高于环境污染效应。