基于分数阶微分方程的木马病毒传播规律

叶星旸

(集美大学理学院， 福建 厦门 361021)

0 引言

随着信息传播速度的加快和计算机的普遍使用，信息安全问题成为了人们关注的一大热点，木马病毒的出现也极大威胁了信息安全。与其他计算机病毒相比，木马病毒更具有“伪装性”，木马病毒通常以看起来无害的程序为载体存在于用户的电脑中，一旦用户触发了相关的网页或者软件等，程序就开始运行，然后夺取用户的控制权，从而达到窃取资料的目的。因此，研究木马病毒的传播规律从而找出有效控制木马病毒传播的措施，是非常有必要且具有重要的意义。

由于计算机病毒与生物病毒高度相似，因此，可以利用经典的流行病仓室模型来研究计算机病毒的传播规律，这方面已有大量的研究结果[1-8]。例如，文献[1-2]考虑了计算机病毒的SIRS模型，文献[3-4]研究了具有潜伏期的SEIR模型。然而，上述这些研究结果都是基于整数阶微分方程模型。

近几十年来，由于一些学科新现象新定律的发现，分数阶微积分已成为一个研究热点。随着分数阶微分方程的发展，分数阶模型更加接近实际情况，能对生物系统进行更为细致深入的研究，越来越多的研究者也开始关注分数阶传染病模型[9-10]。然而，目前尚无文献考虑利用分数阶方程模型来研究木马病毒的传播情况。而且，分数阶微分方程在研究一些具有记忆过程、遗传性质、异质材料及远程扩散过程比整数阶方程模型更具有优势。木马病毒通过将自身伪装吸引用户下载执行，向施种木马者提供打开被种主机的门户，使施种者可以任意毁坏、窃取被种者的文件，甚至远程操控被种主机。经典的整数阶方程如反应扩散方程就很难准确地描述木马病毒的这种远程操控和大范围传播的扩散现象，而分数阶导数的全局性使得分数阶微分方程能更准确地描述木马病毒的这种远程扩散现象。因此，本文通过建立合适的分数阶微分方程模型研究木马病毒的传播规律。

1 木马病毒传播模型

由于木马病毒一旦被计算机用户触发，则电脑立刻中病毒，因此木马病毒几乎没有潜伏期。基于此，假设在木马病毒传播范围内的计算机用户有3种类型：1)易感者S，指尚未感染木马病毒并有可能感染病毒的用户，在t时刻其数量记为S(t)；2)感染者I，指已经感染木马病毒的用户，在t时刻其数量记为I(t)；3)免疫者R，指具有免疫不会再感染木马病毒的用户，在t时刻其数量记为R(t)。木马病毒在计算机间的传播情况如图1所示。

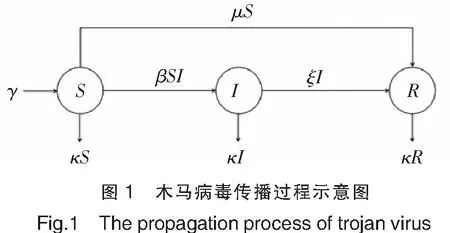
图1中：γ为t时刻进入系统的计算机用户数量；μ表示易感者因为安装木马补丁成为免疫者的比例；β为感染率，指的是在一定时间内，易感者因为没有安装木马补丁而感染上木马病毒，由易感者转变成感染者的计算机总数为βSI；ξ表示感染上木马病毒的计算机在进行杀毒后打补丁或升级系统从而获得永久免疫的比例。考虑到计算机用户在关闭计算机之后，木马病毒不再活跃，因此t时刻有κ比例的用户从易感者、感染者、免疫者移出系统。根据以上假设，建立如下的木马病毒传播的整数阶微分方程模型：

(1)

借鉴文献[11]的方法，在模型(1)的基础上引入分数阶导数，得到如下的分数阶微分方程模型：

(2)

2 解的有界性及唯一性

为证明本节的结论，需要用到下面的几个引理。

下面给出主要定理。

证明假设当t=0时，S(t)=0。首先证明S(t)≥0,∀t≥0。假设S(t)≥0,∀t≥0不成立，则存在t1>0,使得当0≤t0,当t=t1时，S(t)=0,当t>t1时，S(t)<0。

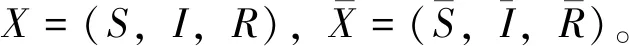
(3)

3 平衡点

定理3 当R0<1时，模型(2)有唯一一个未感染平衡点E0(γα/(μα+κα),0,μαγα/[κα(μα+κα)),当R0>1时，模型除了一个未感染平衡点E0外，还有一个感染平衡点E*(S*,I*,R*)，其中S*=(ξα+κα)/βα,I*=[βαγα-(ξα+κα)(μα+κα)]/(βα(ξα+κα))=(μα+κα)(R0-1)/βα,R*=(μαS*+ξαI*)/κα。

定理4 当R0<1时，系统(2)的无病平衡点E0局部渐近稳定，当R0>1时，E0不稳定。

证明系统(2)在E0处的Jacobian矩阵为：

(4)

如果Jacobian矩阵J(E0)的所有特征值满足条件[16]|arg(λ)|>απ/2，那么未感染平衡点E0是渐近稳定的。容易求得J(E0)的所有特征值为λ1=-κα<0,λ2=-(κα+μα)<0,λ3=βαγα/(μα+κα)-(ξα+κα)=(ξα+κα)(R0-1),。显然，当R0<1时，λ3<0,于是，J(E0) 的所有特征值均为负实数，从而条件|arg(λ1)|>απ/2,i=1,2,3满足，未感染平衡点E0是局部渐近稳定的；当R0>1时，λ3>0，未感染平衡点E0不稳定。

定理5 当R0>1时，系统(2)的地方病平衡点E*局部渐近稳定。

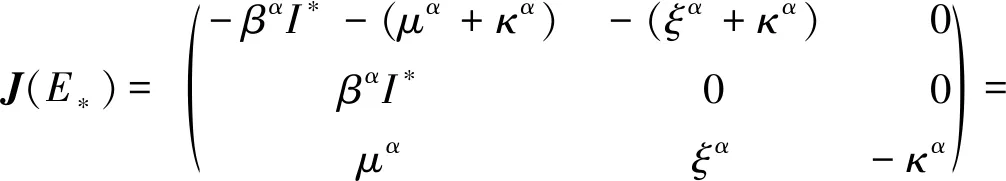
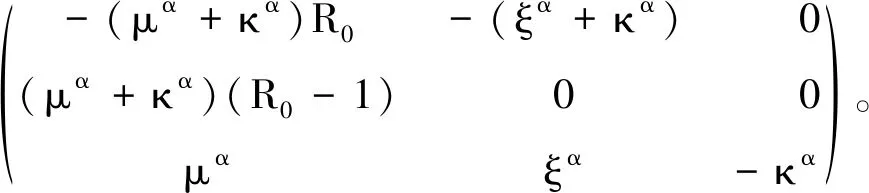
(λ+κα)[λ2+(μα+κα)R0λ+(ξα+κα)(μα+κα)(R0-1)]=0。

(5)

易知λ1=-κα<0是J(E*)的一个特征值，J(E*)的另两个特征值λ2和λ3是方程λ2+(μα+κα)R0λ+(ξα+κα)(μα+κα)(R0-1)=0的根。由韦达定理可知:λ2+λ3=-(μα+κα)R0<0,λ2λ3=(ξα+κα)(μα+κα)(R0-1)。当R0>1时，λ2λ3>0,于是，J(E*)的所有特征值均有负实部，从而条件|arg(λi)|>απ/2,i=1,2,3满足，感染平衡点E*是局部渐近稳定的。

4 数值试验

本节通过对模型(2)的数值模拟来研究模型平衡点的稳定性情况。取定初始值为S(0)=40,I(0)=5,R(0)=10。

表1 α取不同值时模型(2)的基本再生数和平衡点 Tab.1 The basic reproduction number andequilibriums of model (2) for several ααR0E0E∗1227.27(545.45,0,54.545)(2.4,497.8,99.8)0.864.859(144.09,0,22.836)(2.2216,128.81,35.896)0.617.735(37.117,0,9.3233)(2.0928,31.738,12.609)0.59.0928(18.61,0,5.885)(2.0467,15.064,7.3841)

例1 选取参数γ=60,β=0.05,μ=0.01,κ=0.1,ξ=0.02。表1列出了α=1,0.8,0.6,0.5时相应的基本再生数R0、未感染平衡点E0和感染平衡点E*。由定理5知，表1中的感染平衡点E*是局部渐近稳定的。在图2中绘出了模型(2)的解随时间的变化情况，从图2中可以看出，模型(2)的解最终收敛于感染平衡点E*。例2 选取参数γ=60,β=0.001,μ=0.09,κ=0.2,ξ=0.1。当α=0.6和0.8时，通过计算可得相应的基本再生数为R0=0.474 54,0.575。由定理4知，模型(2)只存在唯一稳定的未感染平衡点。图3绘出了模型(2)的解随时间的变化情况，从图3中可以看出，模型(2)的解最终收敛于未感染平衡点E0。

5 结语

研究了一类基于分数阶微分方程的木马病毒传播模型，得到：当基本再生数R0<1时，模型仅存在唯一的局部稳定的未感染平衡点E0，此时病毒得到消除；当基本再生数R0>1时，模型除了未感染平衡点E0外，还存在一个感染平衡点E*，且此时感染平衡点是局部稳定的，病毒将扩散。

为了控制木马病毒的传播，应想办法减少基本再生数的值。注意到基本再生数的形式R0=βαγα/((ξα+κα)(μα+κα))，可以通过减少γ,β的值或者增加ξ,κ,μ的值使基本再生数的值减小。由于γ表示t时刻进入系统的计算机用户数量，κ表示t时刻有κ比例的计算机用户移出系统，所以通常情况下比较难控制γ和κ的值。因此，为减小基本再生数的值，关键在于减小传染率β的值并增加ξ和μ的值。

结合参数的实际意义，给出如下建议：1)对计算机定期扫描系统检查漏洞，并及时安装木马补丁，由此可以增加ξ和μ的值，从而减少感染计算机的数目；2)感染计算机及时退出计算机系统，等到系统漏洞修复完毕之后再联网操作，由此可以减少感染者的数目，从而降低感染率。

此外，由前述数值模拟的结果可以看到分数阶导数的阶数α对模型解的影响。当其他参数固定不变时，α的值越小，基本再生数的值也越小。由定理4和定理5可以看到，当基本再生数从R0>1变化到R0<1时，模型最终的平衡状态将由稳定的感染平衡点变化为稳定的未感染平衡点，由此可以推测分数阶导数的阶数α是模型的一个分岔值。然而，如何从理论上来证实这一推测，分数阶导数的阶数在模型中的实际意义又是什么，这些问题有待在后续的研究工作中进一步探讨。