三自由度球形电机相对坐标检测系统研究

刘婷婷， 凌有铸

(安徽工程大学 安徽省电气传动与控制重点实验室， 安徽 芜湖 241000)

三自由度球形电机作为一种多自由度执行元件已经得到研究人员的广泛关注。一个具备多自由度的球形电机搭载在一个机械关节处，能够有效简化机械结构[1]。目前，针对多自由度电机的研究已经在各个领域中展开，例如：具有多个自由度的超声波电机[2-3]，转子安置永磁体的直流永磁球形电机[4]等。文献[5]设计了新型二自由度球形电机，文献[4]对永磁球形电机应用鲁棒自适应的学习方法，文献[6]使用扩展状态观测器实现球形电机鲁棒动态解耦过程，文献[7]设计了基于多面体划分的永磁直流球形电机。大多数的研究集中在球形电机本体与控制分析层面。

同时球形电机的检测系统也得到迅速发展。美国佐治亚理工学院学者Kok Meng Lee，借鉴传统单自由度电机的检测部件旋转编码器，结合可变磁阻步进球形电机三自由度特性，设计了双滑轨支架的转子位置检测系统[8]。文献[9]设计了双光学传感器的转子位置检测方法，两个光学传感器分别以高刷新频率对转子球体运动过程的变化量进行测量。合肥工业大学以美国GregoryS.Chirikjian等人提出的永磁步进球形电机的模型，对球形转子表面进行随机编码喷图，在16个球形定子线圈上安置96个光电传感器进行位置检测[10]，文献[11]在[10]的基础上借助遗传算法和最速下降法的思想，实现了转子空间位置定位。对球形电机的位置检测系统做了一系列探索，极大地推动了球形电机位置检测系统的发展。

多自由度球形电机究其结构的多样性，其转子与定子的形状均脱离不出球形的范畴，因此多自由度球形电机的坐标变换具有一定的普适意义。传统坐标变换在球形电机系统中已经得到广泛应用[1]。在考虑空间磁场等因素的磁场坐标系对传统坐标变换进行了定义，定义中将系统的静止坐标系与定子坐标系定义到同一坐标内，随后相关的球形电机的检测研究工作均是基于该研究的基础之上。球形电机的坐标变换大多是参照捷联惯导系统中[12-13]类似的坐标变换提出的。但是传统坐标变换中存在以下局限性：

(1)传统球形电机的转子检测系统多使用位姿检测传感器(倾角仪、陀螺仪等)，此类绝对传感器检测结果为转子坐标系相对于地面坐标系。此类方法在球形电机定子坐标系与地面坐标系重合时有效，当定子球体发生空间运动时，传统检测方法失效。

(2)文献[1]在空间使用方向余弦阵的方法进行空间坐标变换，方向余弦阵在做空间计算时，计算复杂，消耗资源大，对于检测系统的实时性造成一定的影响。

本文针对以上问题，主要做如下工作：

(1)结合传统坐标变换，推广基于四元数的广义相对坐标变换，广义相对坐标变换包含了定子坐标系静止的传统情形。

(2)结合相对四元数坐标变换，给出定子-转子(Ls-Lr)与转子-定子(Lr-Ls)的相对坐标变换算法及相对变换的一些性质。

(3)使用绝对位姿传感器，设计了四元数方法下的相对坐标变换检测系统，解决了相对坐标变换的物理实现问题。

1 三自由度球形电机坐标系

图1 三自由度球形电机内坐标系

三自由度球形电机与常规电机一样由定子与转子组成，常规电机的转子只能绕着其固定的输出轴旋转向外输出电机转矩，而球形电机并无机械机构对旋转轴进行限位。结构如图1所示，当球形电机转子绕某一指定轴旋转时，转子相对于定子的位置会发生改变，这一变化量将影响到三自由度球形电机的控制策略。

由三自由度球形电机结构可知，三自由度球形电机的转、定子相对坐标变换时，通常需要建立3个基本坐标系，分别为定子坐标系Ls、转子坐标系Lr和地面坐标系L0。

在三自由度球形电机的坐标系定义中，本文对球形电机的结构做如下假设：

假设1.1 ①假定三自由度球形电机的定子、转子均为光滑完整球体，定子和转子之间无接触摩擦；②假定三自由度球形电机的定子球心与转子球心完全重合于点O，不存在偏差δ；③假定三自由度球形电机做理想旋转运动，运动过程中无位移偏差Δ。

定义1.1 固定于地球表面的某一三维笛卡尔直角坐标系(X0,Y0,Z0)符合右手螺旋规则，坐标系原点O与定子、转子球心重合。设OX0指向地面某一方向，OZ0轴铅垂于地面向上，称为地面坐标系，记为L0。

定义1.2 固定于三自由度球形电机定子的某一三维笛卡尔直角坐标系(Xs,Ys,Zs)，坐标系原点Os与定子球心重合。OXsYs平面与定子球体赤道平面重合，OZs轴垂直于平面OXsYs，指向球形电机定子球体的北极，称为定子坐标系，记为Ls。

定义1.3 固定于三自由度球形电机转子的某一三维笛卡尔直角坐标系(Xr,Yr,Zr)，坐标系原点Or与转子球心重合。OXrYr平面与转子球体赤道平面重合，OZr轴垂直于平面OXrYr，指向球形电机转子球体北极，称为转子坐标系，记为Lr。

注1 笛卡尔坐标系符合右手螺旋规则，地面坐标系非惯导系统中的大地坐标系。地面坐标系以地面为基准，被作为参考坐标系，测量的所有的坐标系旋转量都是相对于该坐标系的旋转量。

注2 如图1所示，除了地面坐标系以外，定子坐标系与转子坐标系并非静止的，转子坐标系随着转子球体转动，整个坐标系均在不断变化中。文献[1]第2.5.3节对三维电机坐标系进行定义，将定子坐标系默认为一个静止坐标系。然而在球形电机的应用中，例如机械关节处，定子坐标系并非静止，也可能随着定子在关节处旋转而旋转，此时传统的设计方案将失效。

三自由度球形电机的定子线圈的位置与转子的永磁体间的相对位置是球形电机控制策略的重要一环。同时对球形电机的位姿测量多采用姿态传感器对转子旋转的欧拉角进行测量[14]，而姿态传感器所获得的结果是转子坐标系Lr相对于地面坐标系L0的坐标。这使得在定子做空间运动时，取得定子线圈与转子永磁体间相对位置的计算失效，结合三自由度球形电机的坐标系下分析，传统坐标方法无法解决定子做空间运动的情形。因此，使用四元数方法来解决三自由度球形电机相对坐标变换。

2 四元数与群旋转

四元数在惯导系统及群旋转中已经得到大量应用，与之类似，可以用以解决群旋转问题的方法是方向余弦阵，而方向余弦阵方法因为计算复杂度和运动奇点问题现在较少应用。四元数基本解析式为A=a0+a1i+a2j+a3k，式中i、j、k满足i2=j2=k2=-1、ij=-ji=k、jk=-kj=i、ik=-ki=-j，同时四元数满足乘法分配律、结合律等性质[15]。使用A的四元数即可表示一个群旋转。

引理1 三维空间中任一矢量α绕轴n旋转角θ获得的矢量β表示该旋转四元数，则βQ=QαQ。

注3 引理1中矢量α、β均是三维笛卡尔直角坐标系下的坐标，在做四元数运算时，应将三维矢量α、β扩充到四元数的虚部，矢量α、β扩展成四元数表达形式为αQ、βQ。Q-1是旋转四元数Q的逆。

3 相对坐标变换

3.1 相对坐标变换四元数算法

目前，转子坐标系折算到定子坐标系下，传统方式为使用方向余弦阵换算，在传统方法中作了定子坐标系与地面坐标系重合的假设[1]。

算法1 传统方向余弦阵计算方法。

Step1 定义符合定义1.1和定义1.3的转子坐标系Lr、地面坐标系L0；

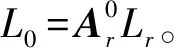
由第1节球形电机坐标系统的分析可知，传统的坐标变换方法在定子坐标系Ls与地面坐标系不重合时失效。因此，给出基于四元数的Ls-Lr相对坐标变换方法。

算法2Ls-Lr相对坐标变换。

Step1 定义符合定义1.1—定义1.3的转子坐标系Lr、定子坐标系Ls及地面坐标系L0；

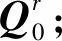
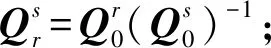
同理，给出Ls-Lr的相对坐标变换，实现转子坐标系变换到定子坐标系中。

算法3Lr-Ls相对坐标变换。

Step1 定义符合定义1.1—定义1.3的转子坐标系Lr、定子坐标系Ls及地面坐标系L0；

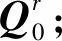
3.2 相对坐标变换的检测平台

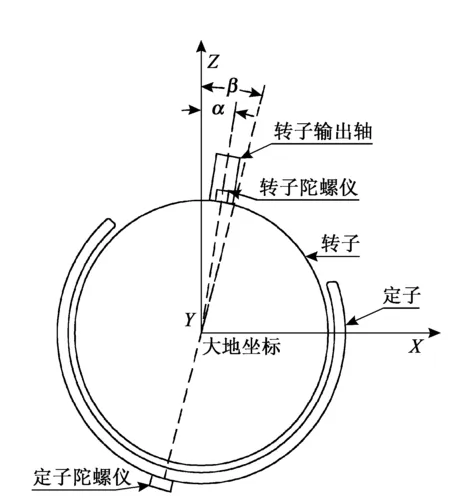
图2 球形电机的检测系统

现今对球形电机的位姿测量多采用绝对位姿传感器对转子旋转的欧拉角进行测量[15]，此类绝对位姿传感器多为多轴MEMS陀螺仪，采集的数据为传感器相对于地面参照的旋转欧拉角。

使用相对坐标变换来解决定子发生空间旋转的问题，应用3.1节中的算法2和算法3，做出如图2所示的改进。

(1)对球形电机转子北极与定子南极各安装1个绝对位姿传感器(六轴陀螺仪MPU6050)；

(2)应用相对坐标变换的算法2和算法3进行两个变换：转子坐标系Lr到定子坐标系Ls坐标系的相对坐标变换，定子坐标系Ls到转子坐标系Lr坐标系下的相对坐标变换。

定子陀螺仪获得定子坐标系Ls相对于地面坐标系L0的旋转欧拉角，以及转子陀螺仪获得转子坐标系Lr相对于地面坐标系L0的旋转欧拉角。

在设计球形电机相对检测平台时，因为姿态绝对位置传感器输出的角度为欧拉角，不能直接应用于四元数的空间运算，还需用到下述引理。

引理2[16]以X-Y-Z顺序的三维直角笛卡尔坐标系下的欧拉角为α、β、γ，则三维欧拉角到四元数的转换公式满足

(1)

图3 检测系统硬件构成

检测系统硬件结构如图3所示，定子陀螺仪和转子陀螺仪对球形电机的定子、转子旋转角度检测数据经由USB转TTL电路发送给上位机，上位机使用LabVIEW调用MATLAB脚本进行处理。

图4 检测算法流程图

该方法使用绝对式传感器，传感器的测量值为相对于大地坐标下的绝对变换值，保证了在连续工作情形下，与球形电机当前位姿无关，可以实现连续坐标变换。

4 数值计算

4.1 传统坐标变换与相对坐标变换

坐标变换分传统坐标变换与相对坐标变换两种情况分别讨论。首先举个极端的例子，取定子球体上北极点(0,0,1)，若转子绕Y0轴旋转90°，则该点在传统坐标变换下对应于转子坐标点为(1,0,0)。

在上述情形下，若定子也绕着Y0轴旋转了90°，在该种情形下，转子与定子应当视为未发生相对旋转，则Ls系统下的(0,0,1)相对于Lr坐标下仍为(0,0,1)。而根据传统坐标变换，坐标变换未考虑定子坐标变换情形，获得坐标变换视为错误情形。

对传统坐标变换与Lr-Ls坐标变换进行坐标数据比对。假设定子坐标点S(1,0,0)，转子绕旋转轴n(0,1,0)旋转1°～90°。定子绕旋转轴n(0,1,0)旋转20°。传统坐标下变换结果在三维图中显示如图5(a)所示，而Lr-Ls坐标变换如图5(b)所示，图中点A为原始数据点，点B为旋转1°所对应坐标变换，点C为旋转90°对应的坐标变换。对比情形下可以观察到传统坐标变换下的数据相当于绕着(0,1,0)旋转了-1°～-90°，在Lr-Ls坐标变换中因为考虑了定子绕着(0,1,0)旋转20°，实际相当于转子绕(0,1,0)旋转了19°～-70°。

(a) 点S(1,0,0)传统坐标变换下坐标 (b) 点S(1,0,0)Lr-Ls坐标变换下坐标 图5 传统坐标变换与Lr-Ls相对坐标变换

4.2 Ls-Lr坐标变换与Lr-Ls坐标变换

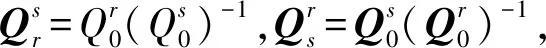
选择新的点S(0,0,1)，转子坐标系Lr绕旋转轴n(0,1,0)依次旋转1°～90°，获得90个旋转角度，定子坐标系Ls绕旋转轴n(0,1,0)旋转30°。则在Lr-Ls变换与Ls-Lr变换中，两者对相同的坐标旋转下，坐标变换结果是关于旋转轴n(0,1,0)对称的。

如图6所示，图中点A为原始数据点(0,0,1)，点B为旋转角度1°(起始点)所对应的坐标变换，点C为旋转角度90°(终点)所对应的坐标变换。图6(a)Lr-Ls坐标变换的起始点B与图6(b)Ls-Lr坐标变换的起始点B是关于旋转轴n(0,1,0)对称的。同理可以观察到终点C。

(a) 点S(0,0,1)Lr-Ls坐标变换下坐标 (b) 点S(0,0,1)Ls-Lr坐标变换下坐标 图6 Lr-Ls坐标变换与Ls-Lr坐标变换

4.3 实际传感器数据变换结果

数据仿真结果验证了算法2、算法3的正确性，实际相对坐标变换需要借助公式(1)来完成，借助六轴MEMS陀螺仪对转子系统的姿态进行检测。

选取转子上点R(0.707 1,0,0.707 1)，转子的旋转数据由传感器获得，采样了50个转子旋转的数据。在假设定子绕旋转轴n1(1,0,0)旋转0°、30°、60°、90°的情形，转子上点做50次旋转后Ls-Lr坐标变换的结果如图7所示。

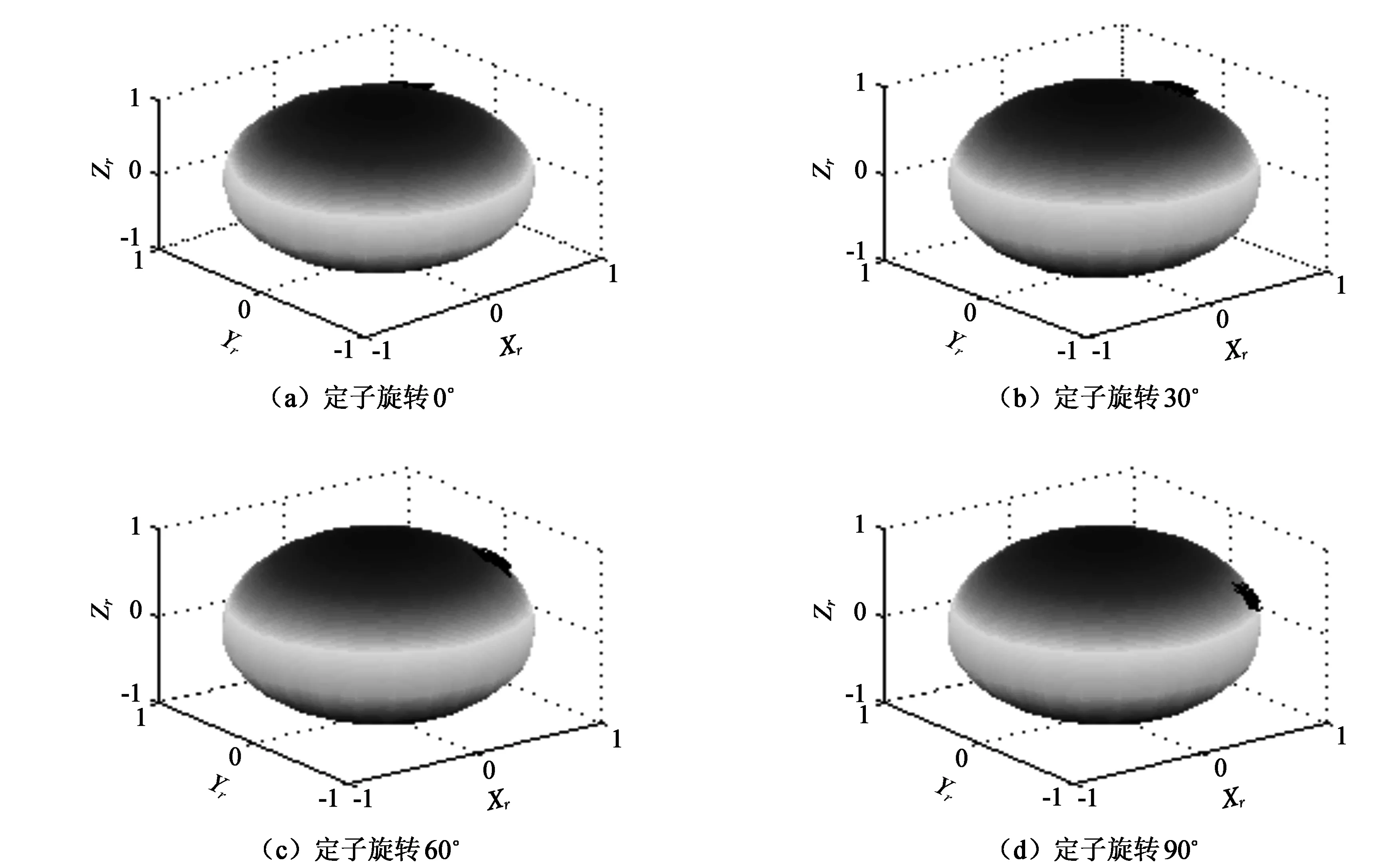
图7 转子传感器数据变换

由图7容易得到，定子旋转0°时，变换结果与传统坐标变换结果一致。定子旋转30°、60°、90°，相当于原坐标系的坐标数据绕着(1,0,0)旋转0°、30°、60°、90°。与实际情形一致。结果验证正确。

5 结 论

相对坐标变换算法的意义较传统方法应用更加广泛，传统坐标变换的应用受限于定子静止的状态。而相对坐标变换可以使用绝对式传感器对球形电机的转、定子位姿进行检测。并可以推广应用到多自由度场景，例如具有高自由度的机械臂系统中，机械臂的运动中会带动关节处电机的定子做空间运动，使用相对坐标变换容易求得电机各参量之间的折算关系。

在现有传统坐标变换方法中，从理论角度推广到相对坐标变换系统中，提供了相对坐标变换解决三自由度球形电机的空间运动的新坐标变换。该坐标变换方法相对传统坐标变换方法具有广义的普适性，而传统坐标变换则可以定义为相对坐标变换方法的一种特例，具有更好的推广应用价值。