基于主动加热光纤法的土中含水率测定与蒸腾分割模型评价
张晓明,施 斌,曹鼎峰,张 岩,孙梦雅,魏广庆
(1. 南京大学地球科学与工程学院,江苏 南京 210046;2. 苏州南智传感科技有限公司,江苏 苏州 215123)
植被的发育直接影响到人们生活的生态环境和地质灾害的发生,如浅层边坡破坏、地表侵蚀、水土流失、沙尘暴天气等[1],因此,研究植物与土中水分场之间的相互作用对于生态环境保护和地表地质灾害防治具有重要意义[2]。
植物对土的工程性质的影响可分为两个方面。一方面是根系对土的加筋作用。目前国内外学者已对此展开了大量研究,提出了不同的加筋模型[3-4],但由于植物与土之间的水力作用缺乏系统的研究,建立的相关分析模型经常失效。另一方面是植物的水力作用导致土中含水率的改变,进而影响土的强度,导致水土流失等灾害的加剧[5]。评价植物对土中水分场影响的根系吸水模型可分为微观模型和宏观模型。微观模型主要基于单根尺度上的水力机制,用来描述根吸收水分的过程机理[6]。宏观的根系吸水模型将根—土系统作为整体分析,不需要考虑植物根系吸水的全部过程机理,也不需要研究其非常复杂的参数[7]。宏观模型基于考虑因素和选取参数的不同又分为两大类,即电学模拟模型和权重因子类模型。前者没有充分考虑土水势、根系以及土壤对水流阻力的影响,后者将根系与植物的蒸腾作用联系起来,蒸腾分割模型就是其中一种。该模型将蒸腾吸水按照一定的权重因子在不同深度的土层进行分配,从而确定根系吸水模型[8]。相较于微观模型,宏观模型多直接应用在田间或野外,发展迅速。如Feddes[9]基于根系密度近似均匀分布的假设提出的根系吸水模型,认为植物根的吸水速率在不同深度土层处为定值;Van Genuchten[10]提出了非线性的根系吸水模型;罗毅[11]等人在Feddes模型的基础上提出了根系密度分布函数的概念;邵明安[12]等人得到水分胁迫下根系吸水的指数模型。
尽管已有大量根系吸水模型及改进形式被提出,用于描述植物蒸腾对土的性质影响,但是,目前还缺少原位含水率的精确测量技术和方法而影响了植物与土之间水力作用的准确评价。如Garg和Leung[13]等人利用张力计以及湿度计定点测试并分析了土的含水率、吸力以及蒸腾作用对土中水分运移的影响,但定点传感器无法高分辨率地获取根系周围水分场的连续时空分布信息,数据量少,准确性较差。因此,本文采用了主动加热光纤法(Actively heated fiber optic,简称AHFO),对植物根系周围土中含水率的变化进行实时分布式测定,根据测定结果评价了蒸腾分割模型,并对其有效性进行了讨论。
1 蒸腾分割模型
1.1 模型基本原理
蒸腾分割模型认为植物根系吸收的水分90%以上被蒸腾散失,只有不到10%的水分用于自身的新陈代谢等其他方面[14]。该模型将潜在蒸腾量定义为有效根区深度范围内根系吸收水分的积分,然后按照一定的权重分配到不同深度的土层。权重因子一般用根长密度分布表示,进而得到相应深度土层植物根的吸水项:
(1)
sp(z)=β(z)Tp(2)
式中:Tp——潜在蒸腾量/(mm·d-1);
a、b——有效根区深度的边界值/(cm);
sp(z) ——z深度处水分吸收量/(mm·d-1);
β(z) ——z深度的根长密度/(mm·cm-3)。
由于植物处于室内,其环境因素可能导致有效蒸腾量与潜在蒸腾量相差较大,影响模拟效果,因此,本文中采用水量平衡法计算得到的理论蒸腾量Ta取代潜在蒸腾量Tp,可得修正后的计算公式:
sp(z)=β(z)Ta(3)
采用水量平衡法[15]计算植物理论蒸腾量:
式中:T1-2——植物某时段的蒸腾量/(mm·d-1);
ρdi——第i层土的干容重/(g·cm-3);
Hi——第i层土的厚度/(cm),本文中每层按1 cm计算;
θ1和θ2——第i层土计算时段的始末含水率/(cm3·cm-3);
M、P、K、C——计算时段内的灌水量、降雨量、地下水补给量以及排水量/(mm)。
本文室内试验中M、P、K的值均为0,C是花盆通过底部小孔排出的水量,为负值。
某计算时段内的植物有效蒸腾量计算公式可简化为:
(5)
1.2 土中含水率AHFO法测定原理
利用AHFO法测试土中含水率的基本原理是,通过将埋入土中的加热型光缆进行通电加热,根据加热型光缆加热后热量向周围土扩散的快慢程度计算土的导热系数,并根据土的导热系数与含水率之间的关系确定土中的含水率[16]。加热光缆通电升温过程中温度与线性热源周围土的导热系数λ的关系为[17]:
(6)
式中:T0——初始温度/(℃);
q′ ——单位长度热源的加热功率/(W·m-1);
t0——与热源尺寸及热源与周围介质接触面有关的时间系数;
d——常数。
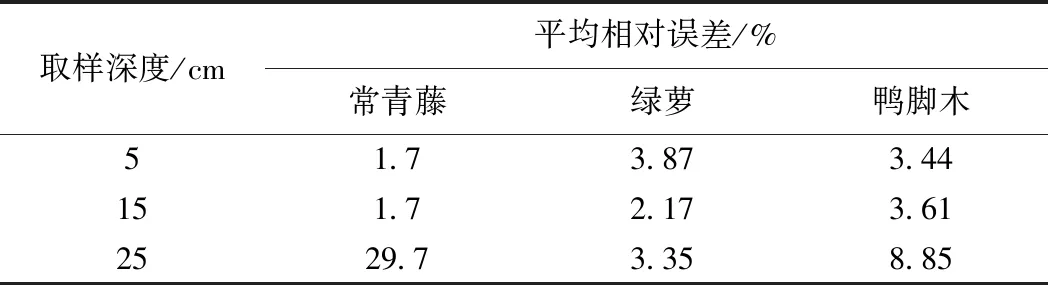
由于t0< (7) 可通过加热过程中t1,t2不同时刻的温度值求出导热系数[8]。传统的描述土导热系数与土中含水率之间的关系主要有4种典型模型,即一次函数模型、对数函数模型、指数函数模型和幂函数模型。基于王铄、Striegl、曹鼎峰等对以上模型的进一步研究和修正成果, 本文采用了曹鼎峰等提出的分段函数模型[16],即含水率较低时采用二次函数模型,含水率较高时采用一次函数模型[16]: (8) 式中:wcr——界限含水率/(m3·m-3); wsat——饱和含水率/(m3·m-3); a、b、c、k0和b0——与土类型相关的常数。 利用拉曼光时域反射测量技术(ROTDR)测定温度。ROTDR是Raman 散射感温效应和 OTDR相结合的新技术,前者用于温度测量,后者对光纤沿线进行空间定位。根据热力学定律,可得Anti-Stokes 光与 Stokes 光的强度比,根据光的传播距离与速率可得激光脉冲注入到接收背向散射光的时间,最后进行温度解调确定实际温度[18]。 (9) 采用分布式光纤温度测量系统监测埋设在土中的碳纤维加热光缆的温度变化,结合温度特征值与含水率的关系,获得土中含水率的分布信息。相对传统的水分场监测方法,AHFO法精度高,数据量多且有效性好,可精准实时监测原位土中含水率的时空分布信息。 为了评价蒸腾分割模型的准确性和适用性,室内试验主要通过监测植物根部土周围含水率的时空分布分析植物—土的相互作用关系。试验装置共设有7个花盆,其中6个花盆种植植物,剩余一个作为裸土对照组。花盆高40 cm,上口直径37 cm,盆底直径32 cm,花盆底部分布有12个透水小孔,小孔直径1 cm。7个花盆底部均匀撒铺5 cm厚的碎石子,作为反滤层。用铁丝制作两组圆柱形铁丝笼,其中一组高30 cm,直径22 cm,另外一组高30 cm,直径25 cm,每组各7个。 试验采用南智传感公司研发的含水率监测系统,精度较高,可实现土中含水率分布式信息的实时获取,系统基本参数见表1。该系统选用光缆型号为62.5/125的碳纤维加热光缆,对光缆进行人为加热,利用升降温过程中的温度特征值与含水率的关系进行土中含水率的分布式监测。为了提高光缆的空间分辨率,将碳纤维加热光缆均匀缠绕在圆柱形铁丝笼上,每个铁丝笼框架上缠绕约6 m的光缆,将直径相同的7个圆柱形铁丝笼串联在一起,首尾端各预留出10 m的冗余段。试验设备主要包括变压器、铜导线、植物补光灯、光缆。 表1 分布式含水率测试系统相关技术参数Table 1 Related technical parameters of distributedmoisture content test system 将缠绕好碳纤维加热光缆的2组不同直径的圆柱形铁丝笼分别放入底部铺有碎石子的花盆中,然后再将调配好的土装入。在装土过程中,每隔5 cm进行压实处理,填土完成后将植物移载到花盆中。 试验仅选用砂土和黏土质量比为6.6∶3.4的混合土,该类型土在浅层滑坡常见,且较为适宜3种植物的正常生长。为了土样拌合尽量均匀,分批次、分阶段进行搅拌。土样的干密度为1.31 g/m3,饱和渗透系数为1.50×10-6m/s,级配曲线见图1,不均匀系数为3.18,曲率系数为1.15。土水特征曲线见图2,在建立含水率与基质吸力关系时,选用Van Genuchten模型[19]。 图1 土样的级配曲线Fig.1 Size distribution of soil particles 图2 土-水特征曲线Fig.2 Soil-water characteristic curve 试验选用的植物共有3种,每种植物各两盆,并对其进行编号,1、2号花盆为鸭脚木树,3、4号花盆为绿萝,5、6号花盆为常青藤,7号花盆为裸土作为空白对照组。3种植物具有不同的生存习性,绿萝气根发达,对水分依赖性强,但需水量较少;常青藤宜排水良好的砂质壤,需水量较大;鸭脚木生命力强,适于环境绿化或边坡防护,需水量介于绿萝与常青藤之间。文章主要研究3种植物蒸腾过程中的水力作用以及不同植物对植物根系周围土含水率的影响情况。因此,在植物的选用方面,3种植物的根长密度、叶面积指数等不作为控制变量,对植物的根系、枝叶发育情况不作统一要求,只需3种植物具有相同的生长年龄并且在试验过程中维持正常的生长状态。 测定植物的根长密度具体试验步骤为:以植株为取样中心,垂直向下挖取边长为25 cm的正方形土块,直到肉眼观察不到根系为止;然后将根系冲洗干净,用直尺测量每根的长度并计量根数,最后得到根系总长度,总长度除以挖取的土样体积求得植物根长密度[20-21],纳入计量的根系径级范围为0.5 ~2 mm,该径级的根系对土中水分的影响最为明显[21]: (11) 在正式监测数据前15d,为了使植物能适应移植后的新环境,以保证在正式监测后正常生长,每天在7个花盆浇灌等量的水、生根液和营养液。其水量、生根液和营养液的添加量,以试验选用的3种植物维持正常生长所需量为依据,但严格控制等量的原则。植物15 d养护结束后,经观察,植物已经适应了新的土气环境状态。此时停止浇灌,室内温度控制在约18 ℃,相对空气湿度约50%。利用AHFO技术进行植物生长过程中水分场监测,同时对植物进行全天候补光,以保证植物在室内进行正常的蒸腾作用和光合作用等。利用加热设备对光缆进行加热时,施加电压为7.18 V/m,每组试验加热时间为20 min,冷却时间为40 min,根据AHFO方法进行监测。前10 d监测频率为1次/d,10 d以后监测频率为1次/3 d。 试验得到的含水率与温度特征值的关系,符合曹鼎峰等提出的分段函数模型,即含水率大于0、小于界限含水率的时候符合二次函数模型;含水率大于界限含水率、小于饱和含水率的时候符合一次函数模型。对于本试验中土样,临界值取0.17 m3/m3,其拟合结果见图3。 土壤含水率与温度特征值之间关系利用最小二乘法拟合,本试验所用土的拟合结果可表示为: (12) 二次函数段相关性系数为0.916,一次函数段相关性系数为0.908 9,均大于0.9,符合一般应用要求。 将试验组中植物土中含水率累积变化量(θcum) 与裸土对照组作差,可得植物所引起的土中含水率累积变化量与时间关系曲线见图4。3种植物花盆中土中含水率随时间变化的规律具有一致性,在试验的前10 d含水率降低迅速。主要原因是开始阶段土中的含水量较为充足,无水分胁迫,植物根内外的水势差较大,植物处于被动吸水的状态,根部土中的含水率变化非常明显。Leung等人研究发现干燥过程的初始阶段含水率降低迅速,土壤吸力恢复较快,与本试验中观测到的结果具有一致性[22]。第10 d以后,土中含水率保持相对稳定的状态,变化量非常小,此时重力水几乎被蒸发散失掉。此时土中细颗粒对水分的吸持力大于等于蒸腾拉力,植物根部仅发生蒸发作用以及由于植物生理活动发生的主动吸水现象。随着蒸腾作用的不断进行,试验装置本身也会损失水分,根部土与根内的水势差随之降低,进一步增加了植物根系吸水的难度,土中含水率变化曲线趋于平缓。 图4 植被所引起的土中含水率累积变化量与时间关系曲线Fig.4 Cumulative change of water content caused by plants with time 对比不同土层深度植物与土水分的作用曲线,得到3种植物都是在15 cm位置处引起的土中含水率累积变化量最大。主要原因是3种植物的有效根系密度约在15 cm处最大,是根部吸水的主要深度,监测结果与试验开始时种植植物的根部位置相符。试验结束后,通过直尺测量法对3种植物的根长密度分布进行计算分析,发现有效根长密度分布主要在10~15 cm范围内。在15 cm深度处,根系发育最好,根长密度最大,直接验证了监测数据的有效性以及植物根系密度分布对根部吸水起着至关重要的作用。植物对土中含水率的影响深度仅局限于土的浅表层。 对比分析3种植物对土中含水率的影响,其中常青藤影响最大,鸭脚木次之,绿萝影响最小。目前,蒸腾分割模型主要采用根系密度分布函数作为权重因子。本次试验在进行植—土水分交互作用分析时,重点考虑了根系分布对植物吸水的影响,将叶面积指数和土水势作为次要因素。试验发现,相较于鸭脚木和绿萝,常青藤在同一深度处的根系密度最大,蒸腾作用最为明显,引起的土中含水率累积变化量约为0.125 m3/m3,为鸭脚木和绿萝的2倍。由于土水势、根密度、叶面积指数、土壤阻力等都会影响植物的蒸腾作用,仍无法确定各种参数的影响权重。 将前10 d各个时段内基于水量平衡法计算得到的植物理论蒸腾量进行拟合,得到理论蒸腾量与时间的关系曲线见图5。鸭脚木、绿萝、常青藤的理论蒸腾量与时间的关系为: 图5 植物蒸腾量与时间关系曲线Fig.5 Plant transpiration with time 植物根长密度为单位土体积的根系长度,试验中采用直尺测定法。此次试验的各类植物的根长密度为: (14) 结合式(3)、(13)和(14),可得某时段土中深度z处根的理论吸水量: 其中,Sp(z,t)表示按照蒸腾分割模型植物在任意时间t和任意深度z的理论吸水量。 将AHFO法监测数据与Sp(z,t)进行比较分析,验证蒸腾分割模型的有效性。选用的深度值z分别为5、10、25 cm,将z值代入式(15),可得不同植物不同时间不同深度的理论吸水量,即蒸腾分割模型计算出的理论蒸腾量。将试验组花盆含水率的累积变化量与裸土对照组的含水率累积变化量作差,得到光纤监测的植物蒸腾量。图6为不同植物不同时间不同深度的理论蒸腾量与监测蒸腾量的对比曲线。 图6 不同植物的理论蒸腾量与监测蒸腾量对比曲线图Fig.6 Comparative curves of theoretical and monitoring transpiration of different plants 通过图6对比可得,理论曲线与实际监测曲线拟合性较好,误差见表2,其中15 cm深的位置拟合性最好。三种不同植物各个数据点的平均相对误差均小于5%,在允许范围内。其原因是该深度受土表面和盆底影响最小,其边界效应可以忽略不计。25 cm处,由于受花盆底部散失水分影响较大,边界效应明显;另外,根系密度分布函数为指数型函数,计算得到的根系密度随深度增加不断增加,实际上,25 cm处根系密度要小于15 cm处,导致理论蒸腾量偏高,拟合结果相对较差。5 cm处虽然接近土的表面,受到土表面水分蒸发的影响,但是在干燥初期,土层表面的蒸发作用相对植物的蒸腾作用来说较为微弱,因此数据拟合较好。将蒸腾分割模型用于分析植物根部土的水分运移规律以及探究不同植物的蒸腾作用对土中含水率的影响是有效的。在降雨入渗或灌溉后的干燥初期,根区不存在水分胁迫,根系吸水情况主要取决于根系分布情况,以根系密度分布函数作为权重因子的蒸腾分割模型简单实用,显示出独特的优越性。 表2 三种植物不同土层深度处蒸腾分割模型计算值相对误差Table 2 Relative errors of the transpiration segmentationmodel at different depths for the three kind of plants 蒸腾分割模型主要从宏观的角度对植物根的吸水机理进行数值模拟,经验性较强。从监测数据对模型的评价结果看,蒸腾分割模型对植物与原位土水分交互作用的模拟较为有效。但是从个别数据点的误差看,蒸腾分割模型在权重因子函数的选择和动态跟踪上有很大的完善空间。大多数蒸腾分割模型都是基于根系密度分布随土壤深度变化的一维模型,忽略了植物生长过程中物理、生理和水力机制的影响,模型参数设置有待完善[23]。根系密度分布函数是基于不同深度土层的根长建立,模型认为是不变的,实际上根系吸水项是与根系有效吸水表面积有关,且随着根系的生长衰败发生动态变化[24-25]。在蒸腾分割模型不断完善过程中,建议更多地借助于计算机技术,实现多维动态的描述根—土水分交互作用[8]。 (1)AHFO法监测结果显示,植物对土中含水率的影响可用蒸腾分割模型进行有效描述,含水率变化受植物叶面积、根系密度、土层深度和蒸腾时间的影响。 (2)本试验中选用的绿萝与鸭脚木叶面积指数和根系密度相近,二者引起根部周围土中的含水率变化值也相近,为0.075 m3/m3,常青藤的叶面积指数和球状根系密度远远大于绿萝与鸭脚木,因此,常青藤引起的根部周围土的含水率变化值远大于其他两种植物,为0.125 m3/m3。 (3)本次试验中,植物对土中水分运移的影响主要是土的表层10~15 cm深度范围内,深部位置的水分场几乎不受植物的影响。 (4)湿润事件之后的干燥初期,含水率下降明显,吸力得到迅速的恢复,随着干燥时间的延长,植物对土中水分的影响逐渐减弱。在植物土的水分交互过程中,相比较于蒸腾拉力产生的主动吸水,植物在土水势作用下的被动吸水占据主导地位。
2 室内试验
2.1 试验方案



2.2 数据采集
3 试验结果及分析
3.1 土中含水率与温度特征值的关系拟合
3.2 不同植物根系周围土中含水率监测

3.3 根系吸水蒸腾分割模型评价
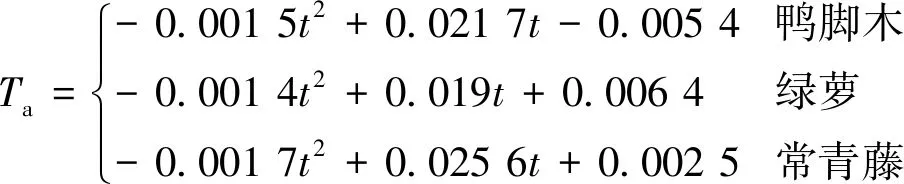



4 结论

