金属材料非平衡相变的热/动力学协同

张玉兵，王 慷，彭浩然，张 旭，陈豫增，刘 峰

(西北工业大学 凝固技术国家重点实验室，陕西 西安 710072)

1 前 言

所谓相变，是指在一定驱动力下通过原子结构的重组而降低系统Gibbs能的过程。根据转变速率和转变分数对温度和时间的依赖性，自然界中的大多数相变被划分为切变型马氏体相变和扩散型形核/生长类相变[1]。金属材料成形中两个紧密关联的物理过程凝固和固态相变大都属于形核/生长类相变。随材料科学发展，有关相变新理论、新技术的研究日新月异；这些已取得的成就大都基于热力学(thermodynamics)和动力学(kinetics)。新理论旨在描述非平衡相变，新工艺则是利用非平衡相变；两者在结构材料设计方面均起到立竿见影的效果，但是，依然无法解决困扰学术界和工业界多年的一大难题，即基于整体加工过程的微观组织预测和面向目标组织性能的调控工艺确定。究其根本，当前技术通过改变一种或多种工艺参量来进行组织调控，相对忽视了相变理论的指导；当前理论大都属于唯象模型[2]或隐含大量物理假设的解析模型[3]，即便有相场、第一原理计算等介入，也是针对某物理量或某平衡态的表述[4]，缺少真正从热/动力学协同来解决问题。

大量相变理论和技术成果表明，热力学与动力学不是完全独立而是相互关联[5-10]。材料加工涉及的相变大都属于复杂变形、温度及冷却或加热条件下的非平衡动力学过程；如果能够将微观组织状态、非平衡效应及形变的综合影响同热/动力学函数耦合，进而开展面向目标组织、性能的加工条件(热/动力学)的协同性调控，那么，基于整体加工过程的微观组织预测和面向目标组织的调控工艺确定便可以实现。这种“基于热/动力学协同的非平衡相变组织预测”旨在研究热力学驱动力和动力学能垒间函数关系，以及热力学驱动力、动力学能垒同微观组织及力学性能间理论关联。也就是说，材料加工调控组织，进而决定材料随后的变形机理和力学性能；以微观组织调控为纽带，如得到材料加工所涉及相变的热力学和动力学同微观组织及其关键力学性能(变形机理)之间的关联，便可以对调控工艺进行有针对性的设计，从而更大限度、更直接、更有效地提高材料力学性能。

2 热/动力学协同的发展历程

前人取得的相变理论成就可大致分为热力学和动力学两方面[11, 12]。热力学描述体系状态，主要针对自由能、焓值等热力学参量和相应材料性质的变化，旨在研究平衡系统各宏观性质之间的相互关系，揭示变化过程的方向和限度[11, 12]；动力学针对体系状态参量随时间的演化，依赖转变路径而主要探讨能垒、转变速率及体系特征参量(新相晶核数量、尺寸、相分数等)的演化问题[1, 11, 12]。这些理论主要基于经典平衡态热力学、唯象不可逆热力学和统计力学；经典热力学主要用于计算材料相图及相关性质；不可逆热力学主要从非平衡过程能量耗散方面研究非平衡体系的介观、宏观尺度演化；而基于统计力学的理论主要从原子尺度出发，结合团簇动力学，发展相变的热力学/动力学理论。

从热力学和动力学的角度考虑，非平衡相变作为金属材料热加工领域重要的基础性问题，其发展历程可从以下3方面进行阐述。

2.1 如何处理工艺条件与相变路径的关系

在成分给定的前提下，工艺条件决定相变路径是材料加工中的基本常识。图1a为Al-Mg合金喷溅淬火所得薄带截面，表面冷却速率较高处形成均一的过饱和单相固溶体，组织内部冷却速率较小处形成典型共晶组织；由于凝固机制突变，两种组织间存在明锐过渡[13]。图1b为熔体旋转法所得Ni-18B(原子分数，%)合金薄带纵向截面组织[14]，从与辊轮接触表面向自由表面方向，随冷速降低，出现无偏析单相组织向枝晶组织的转变。类似地，Liu等[7]在Fe-0.01C(原子分数，%)合金奥氏体化后冷却过程中发现，随冷速增大，γ/α相变开始温度降低，且相变机制由扩散控制向界面控制转变；当冷速足够大时，只发生界面控制的块体转变(图1c)。

以上实验事实表明，热力学与动力学不是完全独立而是相互联系的，当工艺变化导致热力学条件改变时，相变路径和动力学机制相应发生变化。在原子尺度，一阶相变通过热激活发生，属于稀有事件(rate event)，其理论描述基于过渡态理论[15]，其速率方程如式(1)：

(1)

其决定性因子是热力学驱动力(ΔG)和动力学能垒(Q)。随热力学条件变化，相变路径或机制的变化可通过动力学能垒来体现。该相关性已经在许多一阶相变中得到体现，大多属于“通过具体加工工艺反映驱动力和能垒间关系”，譬如，非平衡凝固中冷速提高导致驱动力增大，凝固动力学控制机制逐渐由溶质扩散转变为热扩散[16]；不同冷速下奥氏体/低温相分解实际展示出热力学驱动力提高(下降)对应动力学能垒下降(提高)的本征规律[10]。可见，热力学体现相变驱动力从而促进相变，动力学虽表现为相变速率但由于受控于能垒而实际体现为阻力；正是由于驱动力和阻力间协调变化，才导致相变路径、相变产物及其形态千变万化。与之对应，有意识地利用或打破驱动力和能垒间规律而指导工艺设计的工作尚不多见。作者课题组据此设计了A356铸造铝合金非平衡凝固与固态相变一体化的处理方法[17]：将大冷速导致非平衡凝固中大驱动力小能垒相变(形成Al(Si)和Si(Al)过饱和固溶体；热扩散控制)同低温固态时效中较大驱动力较大能垒相变(形成Al枝晶基体中的纳米Si颗粒+共晶Si基体中的纳米Al颗粒；溶质扩散控制)结合，形成常规工艺无法获得的多级组织(Al枝晶+共晶Si+Mg2Si析出相+Al枝晶基体中的纳米Si颗粒+共晶Si基体中的纳米Al颗粒，图2)，不改变合金成分和引入外加强化相，且同时提高了合金的强度和塑性(图3)。

2.2 如何处理加工工艺与微观组织的关联

相变产物的复杂组织决定材料最终性能，不同加工工艺下组织演化的理论描述始终是材料热加工领域悬而未决的难题。这方面工作包括3个层次：

(1)一阶相变经典处理方法基于形核/长大的物理图像；从能量变化角度考虑，前者使体系能量升高，需要体系微观起伏克服能垒，在原子尺度发生；后者使体系能量下降而趋于稳定，受原子在界面两侧的跃迁控制，可在原子尺度、介观甚至宏观尺度发生。经典JMA(Johnson-Mehl-Avrami)理论及其衍生[3]是该领域的代表性工作。相变动力学解析模型的理论框架缺乏与微观组织演化的物理关联，所涉及的全转变动力学隶属于平均场理论[18]，其形核和生长速率均为统计平均，可预测转变分数和转变速率随时间或温度的演化规律[7, 19, 20]，但对微观结构及组织形貌演化无能为力。究其原因，形核/生长类理论在描述新相演化时需要追踪界面位置(即界面位置随时间演化)[21]，而工程材料的复杂相变过程中多个界面形貌同时演化，因而该理论难以实现复杂组织演化过程的理论描述。如何将组织参量耦合入热力学势函数，通过考虑随热力学条件变化的形核率和生长速率，建立内涵微观组织参量演化的全转变动力学理论体系，是当务之急。

(2)为避免相变组织演化中的界面追踪问题，Cahn等将序参量及弥散界面概念引入到金属材料相变中，并建立Cahn-Hilliard和Allen-Cahn方程[22, 23]来描述体系保守和非保守序参量的演化，从而提出描述显微组织演化的相场法理论框架。该方法已广泛应用于金属材料涉及的γ/α全转变[24]、相析出[25]、共析转变[26]及马氏体相变[27]。但是，当序参量空间分布复杂时，计算量大大增加[21]，因而，上述适用于二维情形的相变模型不能完全反映实际三维组织特征。此外，相场法首先需要获得相场序参量空间分布，然后统计得到微观组织特征参量，并非直接针对特征参量演化进行描述。

(3)为解决上述问题，作者课题组[28]基于非平衡统计力学认为，发展普适的一阶相变组织演化理论应遵循如下5个步骤：① 考虑拓展团簇和组织特征参量；② 选取代表性微观体系组成的系综描述相变过程；③ 通过非平衡系综原理计算热力学参量；④ 利用最大熵产生原理得到概率密度分布的演化方程；⑤ 将给定时刻微观体系状态的概率密度分布加权平均后得到对应的特征参量。此外，在微观尺度上，形核和长大都是通过原子或分子在新相/母相间界面的吸附与脱附实现，并降低体系能量，因而形核和长大没有明确区别[29]。基于此，作者课题组针对相变组织状态特征参数，采用变分过渡态原理(variational transition state theory, VTST)描述微观热力学、动力学[30]，利用最大熵生成原理(maximal entropy production principle, MEPP)[31, 32]推导体系概率密度的演化方程[28]，可方便地与CALPHAD热力学数据库和原子尺度计算方法结合，同时尽可能减少可调参数的数量。作者课题组还将当前理论框架应用到Al-2Cu(原子分数，%)合金θ′相析出过程和低合金钢组织调控，均取得较好的预测结果[28]。这种基于热/动力学协同的组织预测必然引发出热力学驱动力-动力学能垒-微观组织间关联。

2.3 如何定量理解成分、工艺-组织-性能间关系

成分、工艺-组织-性能作为贯通材料学和材料加工科学的金科玉律，直接导致新工艺和新理论的繁衍不休。虽然说，成分和工艺决定组织，而组织决定性能，真正从此间定量关系出发来实现材料设计，尚未实现。目前大多工作类型可概括为如下3点。

(1)通过成分和/或工艺设计提高性能

以铸造铝合金为例，成分设计通过改变凝固组织而提高合金性能，譬如，在A356铸造铝合金中，加入微量的Ni，V可形成异质核心从而细化晶粒[33]。成分设计也可通过改变最终组织而提高合金性能，譬如，对可明显时效强化的Al-Cu-Mg合金，微量Ag元素的加入可在人工时效过程中抑制S相析出的同时，促进更细小的Z沉淀相大量析出，从而得到很好的强化效果[34]。非平衡凝固旨在利用非平衡效应细化凝固组织、改变溶质元素分布，提高材料力学性能。譬如，提高凝固速度可使A357和A356合金组织显著细化，同时提高Si在Al中固溶度，产生固溶强化效应，提高材料强度[35]。半固态成型技术则通过固/液两相区的温度控制获得均匀形核质点，减少凝固收缩、细化凝固组织，提高铸件力学性能。譬如，Tahamtan等[36]通过半固态成型法制备的A356合金具有微观组织细化、均匀度高、初生α-Al和共晶Si显著球化等特点，具有良好的综合力学性能；而半固态加工与热变形结合，可进一步细化组织、提高组织均匀度，使铸件力学性能进一步提高[37]。目前，铝合金热处理工艺研究主要涉及：① 多级时效；② 同成型方式相配合的热处理制度；③ 同热处理工艺相结合的析出相研究。此类工作不胜枚举，旨在为面向目标性能的析出相设计提供理论及工艺依据。

(2)组织性能唯象关系或物理关系模型

有关组织性能关系的模型工作非常多，大都属于模拟微观组织随应变的变化，然后根据上述组织强度关系，预测应力-应变曲线，即本构模型(constitutive modeling[38])。但真实材料，譬如钢铁、铝合金等，并没有统一的模型预测其应力-应变曲线。当前描述Al合金应力-应变关系的主要模型有：唯象模型和基于位错机制的物理模型[39]。唯象模型中应用最广泛的当属Johnson-Cook(JC)模型[40]。该模型形式简单，参数意义清晰，考虑应变硬化、应变率及温度效应对流变应力的影响，但只能在宏观上对材料性能进行表达，无法在微观或细观等层次对力学性质加以解释。物理模型基于位错机制, 较为著名的是Kocks-Mecking-Estrin (KME)模型[38, 41, 42]。 KME模型最早针对纯Al提出，用于描述局部剪切应变和位错密度的关系；针对Al合金，需考虑析出相对位错存储和动态回复的影响，因此KME模型不断得到拓展[43, 44]，根据物理机制的不同，体系内不同性质的位错如移动位错和林位错[45, 46]、极位错和非极位错[47]、亚结构胞和晶内位错缠结[48]等均得到精细处理与描述。此外，随纳米晶材料发展，晶界效应[49]和晶粒梯度效应[50]也被耦合进位错机制模型。由此可见，目前组织性能关系模型趋向于物理模型发展，模型包含晶粒尺寸、相组分等信息，在变形过程中需要预测位错密度的演化规律。这一态势在QP钢、TWIP钢、TRIP钢、DP钢等钢铁材料中也有所体现[51-54]。这强烈表明，上述组织性能关系模型存在共性，即热/动力学协同有可能影响组织性能关系的具体表现。

(3)考虑关键组织性能的成分和加工工艺设计

近年来，以核心性能为目标，通过组织-性能间物理/经验关系确定材料性能控制单元，定义其在若干个关键节点上(及服役条件下)的组织特征集成参量，进而完成基于热力学、动力学、强韧化机理等物理模型的多尺度建模，建立将目标组织集成变量转换为材料成分与工艺参数的定量评价准则。随后应用合理且高效的优化算法实现高通量备选解集的考察，获得新材料成分与关键工艺的耦合解，并选取若干优选方案进行有限工艺范围内的扩展性实验反馈与验证。基于上述思路，Xu等[55]针对马氏体基体和多种析出相(碳化物、纳米铜颗粒和镍基金属间化合物)，通过遗传算法优化成分(基体Cr含量等)和工艺(奥氏体化、淬火相变以及时效析出)，设计出以板条马氏体为基体并复合多种细小析出相的高强马氏体不锈钢，实现了预期的性能优化。虽然该思路在铝合金中的应用很少见，但同样适用。铝合金第二相(析出相)颗粒的性质、结构、尺寸及分布决定着材料的性能，因而可视为材料的关键组织，通过合理调控时效析出相，可有效改善材料的性能。譬如，Liu等在Al-Cu合金中添加微量Sc元素，能够抑制θ′相粗化[56]，并且能减少纳米晶Al-Cu合金的晶界析出相，提高纳米晶材料稳定性[57]，从而大幅提高材料强韧性。

3 有关热/动力学协同的当前研究成果

目前，有关驱动力/能垒相关性的理论工作很少见报导。结合前人的实验及理论计算，作者课题组分析了非平衡凝固、固态相变及晶粒长大典型过程中驱动力/能垒的变化及其相关性[3, 58-60, 32, 61-64]。这里，选择几个代表性案例从中演绎出热/动力学协同的定量关系，并进一步应用于非平衡相变的微观组织预测。

3.1 纯Fe沿Bain路径的马氏体相变研究

由于Fe的磁性，Fe基合金在结构转变(包括马氏体转变)时的机理并不清楚，即使采用基于密度泛函理论(DFT)的第一原理方法也不能准确解释。究其原因，

DFT计算在0 K进行，没有考虑高温时磁性态的激发。Wang等[61]使用配分函数法(PFA)计算有限温度下磁性构型的波动来研究Fe沿Bain路径的相变热力学和动力学，这是FCC/BCC马氏体转变中最简单的模型。首先，从体积和c/a张成的空间计算基态的能量曲面，分析基态的Bain路径。使用基态物理量作为输入参数，通过准简谐Debye-Grüneisen模型计算每个c/a和体积下的亥姆霍兹自由能，并构建自由能表面，用弦方法搜索最小能量路径(图4a)。在有限温度下，通过MEP(minimum energy path)分析Bain路径的热力学和动力学，观察到由于磁波动引起的自由能差和能垒间的相关性，即转变能垒随驱动力的增大而减小(图4b)。进一步分析此前实验和理论结果，发现该相关性在MT(martensitic transition)中普遍存在，从而控制了工程合金中马氏体组织的形成(图4c)。

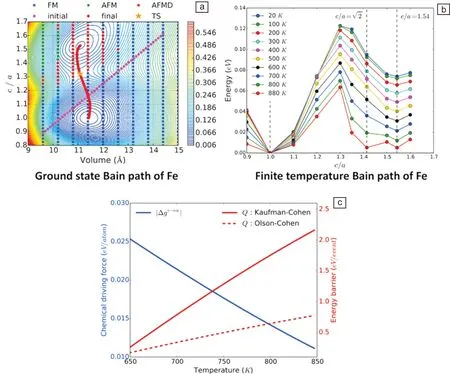
图4 基态纯Fe经Bain路径马氏体相变的能量曲面及最小能量路径(a); 有限温度时纯Fe经Bain路径相变的最小能量路径(b); 纯Fe经Kaufman-Cohen模型及Olson-Cohen模型发生马氏体相变的驱动力与能垒变化(c)[61]Fig.4 MEP for the ground state Bain path: search of the MEP on the energy surface (a); The MEP at finite temperatures along the c/a axis (b); Correlated changes between the chemical driving force and energy barrier for MT in pure Fe from the heterogeneous nucleation models of Kaufman-Cohen and Olson-Cohen (c)[61]

3.2 低合金钢组织调控中的马氏体相变

低合金钢的马氏体相变不单单只受热力学驱动力的控制，动力学能垒也是影响因素之一，综合考虑两者作用，才能对相变动力学过程给出更具物理意义的描述，同时更好地理解该过程中相变热力学与动力学的关系。作者课题组构建了耦合热力学驱动力ΔG和动力学能垒Q的马氏体相变动力学解析式[62]，该式考虑马氏体自催化形核，即马氏体不仅在原奥氏体晶界处形核还在新生马氏体/奥氏体相界面处自催化形核，这两种界面体积密度为SV,γγ，SV,Mγ, 并各自具有不同的形核激活能Qγγ和QMγ，如下式所示：

(2)

在此基础上，引入参数ξ考虑马氏体生长的各向异性碰撞效应，提出了低合金钢板条状马氏体连续冷却过程的全转变动力学理论模型：

(3)

其中mq正比于一个马氏体单元的拓展体积Vex，f是每单位体积内转变分数，上标“ex”表示拓展空间内的转变分数。为了展示模型的特点、验证其有效性，本工作借助Gleeble 3500热模拟机对模型合金Fe-0.2C-1Mn-1Si (质量分数，%)不同奥氏体化条件下的连续冷却马氏体相变进行了实验研究[62]。电子背散射衍射(EBSD)实验分析表明，模型合金在相变中形成了具有多级组织特征的板条马氏体，如图5所示，其中白色实线为初始奥氏体晶粒边界，白色虚线为马氏体多级组织边界。对应的不同奥氏体化条件下的连续冷却马氏体相变动力学曲线见图6。利用耦合热力学驱动力和两种动力学能垒的马氏体全转变动力学模型，采用常数激活能Qγγ和QMγ进行拟合发现：如图7a所示，模型可以很好地描述相变的中高温阶段，但在低温阶段发生偏离，说明恒定激活能只适用于中高温阶段，对于低温阶段数值过大。采用与相变化学驱动力ΔGchem呈负线性相关的Qγγ和QMγ进行拟合发现：

图5 连续冷却(80 K/s)马氏体相变组织的EBSD研究[62]：(a)衍射带对比度图，(b)马氏体多级组织中的晶粒取向Fig.5 EBSD diffraction contrast(a) and orientation image map(b) of the martensite formed in Fe-0.2C-1Mn-1Si alloy with a PAGS of (30±4) μm. The white solid and dash lines in Fig.5b highlight the prior austenite grain boundaries and packet boundaries of matensite, respectively[62]

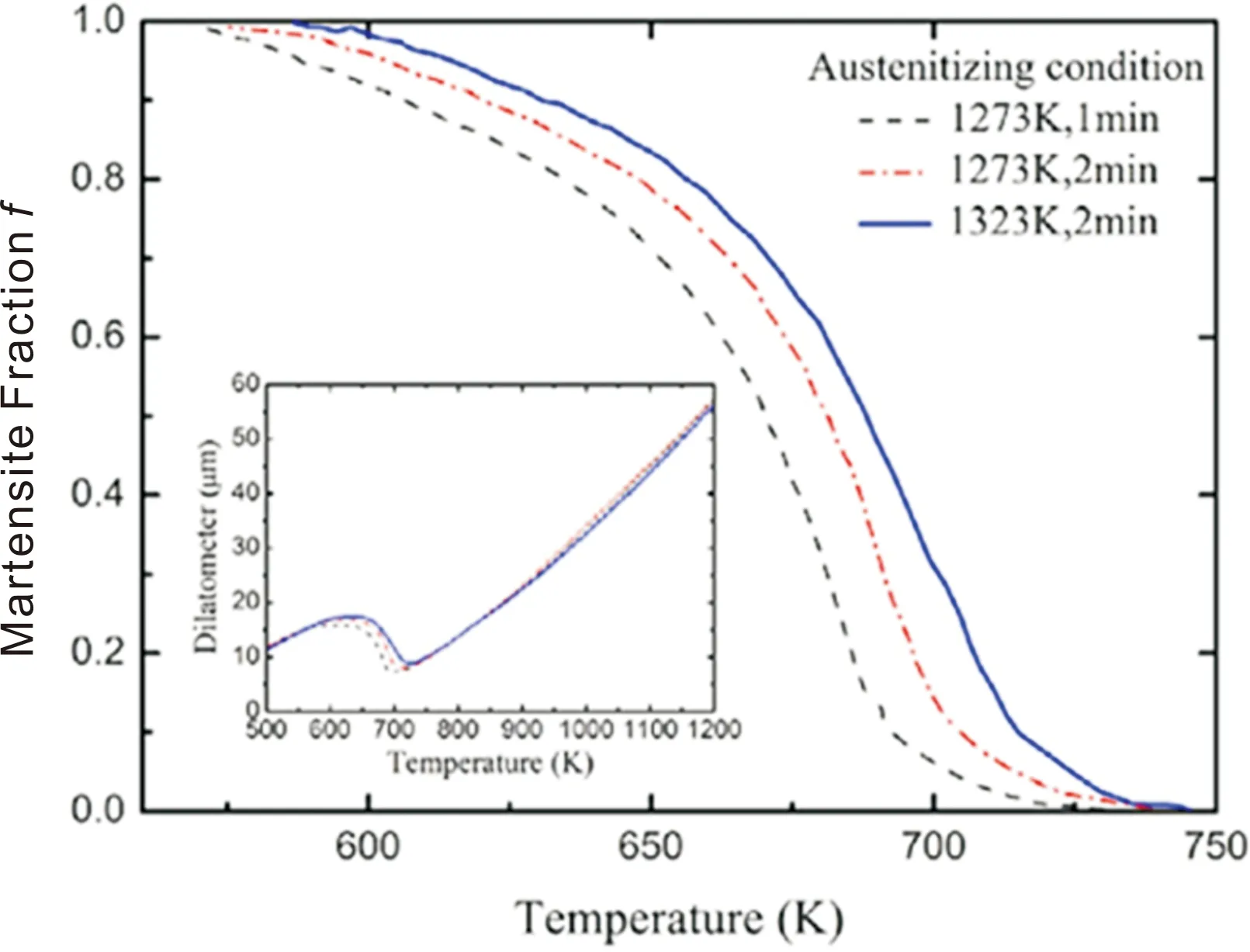
图6 Fe-0.2C-1Mn-1Si合金不同条件奥氏体化后经相同冷却路径的马氏体相变膨胀曲线和相变分数曲线[62]Fig.6 Martensitic transformation expansion curves and phase fraction curves of Fe-0.2C-1Mn-1Si alloy after austenitizing under different conditions with the same cooling path[62]

如图7b所示，模型可以很好地描述整个相变过程，说明马氏体相变的激活能应该是一个随着热力学驱动力变化而变化的量；同时，随着马氏体相变驱动力的增大，其形核动力学能垒减小。这正体现了马氏体相变过程热力学驱动力与动力学能垒间存在着相关性。

3.3 晶界迁移中的相关性规律

晶界迁移决定了晶粒尺寸和形态的演变，因此在多晶材料加工过程中的微观结构演化过程中起关键作用。微观上，晶界迁移是通过热激活小概率事件，调整晶界上的原子构型和降低整个系统的自由能，在晶界附近的原子脱附/吸附来控制的。基于反应速率理论，晶界迁移速度可表示为：

(4)

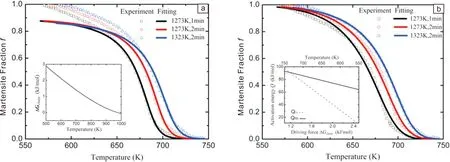
图7 当前理论模型与Fe-0.2C-1Mn-1Si合金实验马氏体相变曲线的对比[62]：(a)采用常数激活能Qγγ和QMγ拟合结果；(b)采用均同化学驱动力ΔGchem呈负线性相关的Qγγ和QMγ拟合结果Fig.7 Comparison between the present model and experimental MT curves[62]. The present experiment were calculated with constant QMγ and Qγγ(a) and non-constant QMγ and Qγγ that varying with ΔGchem in the relationships shown by the inset(b)

其中，ΔG为热力学驱动力(本工作中定义为晶界迁移之前和之后的自由能之间的差异)，Q为晶界迁移激活能，M为晶界迁移率。通常，晶界迁移能垒被认为是与晶界结构相关联的晶界的本征属性，因此与外部条件(例如温度、应力等)无关。虽然在确定各种晶界的移动性方面取得了巨大的成功，但这种研究排除了能垒/驱动力之间可能的相关性。注意到驱动力取决于外部条件，这种相关性如果得到确认，则对晶界迁移的基本规律乃至材料加工过程中的组织演化具有重要意义。作者课题组通过将晶界迁移速率方程与分子动力学模拟相结合来研究驱动力与能垒之间的相关性[63]，其中采用温度热梯度驱动晶界迁移，模拟中构建了29种晶界原子构型，涵盖了所有类型的晶界(即扭转、对称倾斜、非对称倾斜和混合扭转倾斜)。考虑到由五维宏观自由度描述的晶界具有复杂的几何结构，在模拟中全部晶界原子构型采用具有单一结构的平直晶界的双晶模型。为驱动晶界迁移，引入温度梯度，利用晶界自由能随温度增加而降低驱动晶界迁移。如图8所示，以〈100〉Σ5{010}非对称倾侧晶界为例，当晶界从y1位置迁移到y2位置，晶界温度将会从T1升高到T2，相应的晶界自由能从γ(T1)变化到γ(T2)，有研究表明γ(T1)应当大于γ(T2)，从而使得晶界具有向中心位置自发迁移的趋势。作为驱动力来源，本工作对此进行了详细的研究，并获得了晶界自由能随温度变化的具体数值关系。对于稳定温度场中的晶界迁移，迁移驱动力与温度梯度的大小相关，通过改变温度梯度将能够得到不同的晶界迁移驱动力。本工作中，对每种晶界施加10种不同的温度场，获得10个不同晶界迁移动力学过程(图9由于随温度梯度增加，晶界迁移动力学曲线难以区分，对于温度梯度大于5 K/Å的结果中不再展示)。

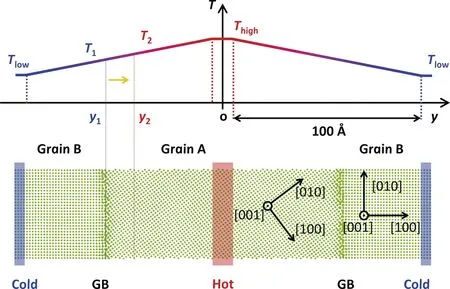
图8 温度梯度驱动晶界迁移示意图[63]Fig.8 Schematic diagram of migrating 〈100〉Σ5{010} asymmetric tilt GB driven by the thermal gradient in the current MD simulations[63]

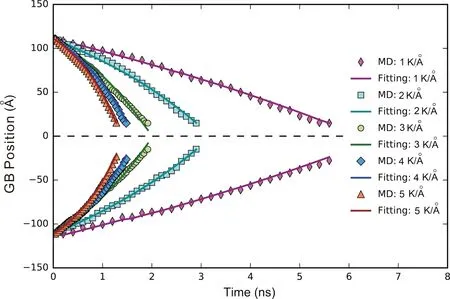
图9 不同温度梯度下，分子动力学模拟Σ5晶界迁移的结果[63]Fig.9 Evolution of the Σ5 twist GB positions under different thermal gradients: MD simulations (symbols) and fittings by the rate equation (lines)[63]

将分子动力学模拟结果和晶界自由能对温度的变化与晶界迁移速率方程相结合，便能够获得晶界迁移的能垒。对比表明，随着热力学驱动力的增加，动力学能垒减小(图10)[63]。这一相关性在不同类型晶界中普遍存在，且相关性具体表现因晶界结构而异。这一相关性的存在，无疑对晶界迁移的基本规律乃至材料加工过程中的组织演化具有重要意义。

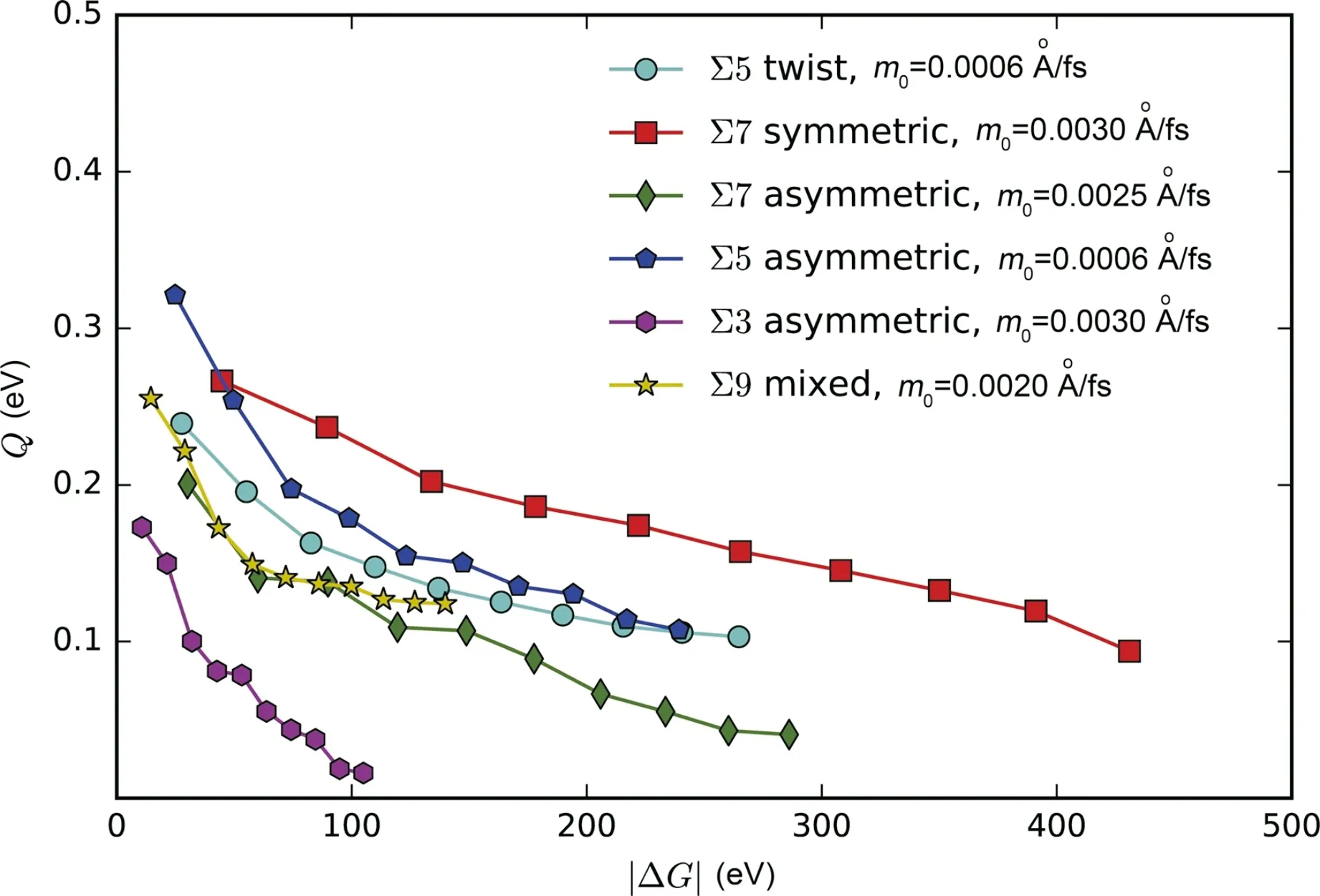
图10 晶界迁移中的热力学驱动力和能垒的相关性[63]Fig.10 Correlation between the energy barrier and the driving force for different types of GBs[63]

3.4 纳米材料中晶粒长大及热稳定性模型

基于Cahn溶质拖拽模型，作者课题组[64]理论推导

了依赖于溶质晶界过剩量的晶界迁移激活能，即：

Q=(1-ΓA)Q0+ΓA(Hseg+Qb)=Q0+ΓA(Hseg+ΔQ)

(5)

公式(5)表明，溶质在晶界的偏析会导致晶界迁移激活能的增大。另一方面，根据Krill，溶质偏析也会导致晶界能的降低：

(6)

结合公式(5)和公式(6)，溶质偏析导致的热/动力学相关性方程可以推导为[64]：

(7)

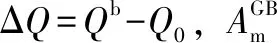
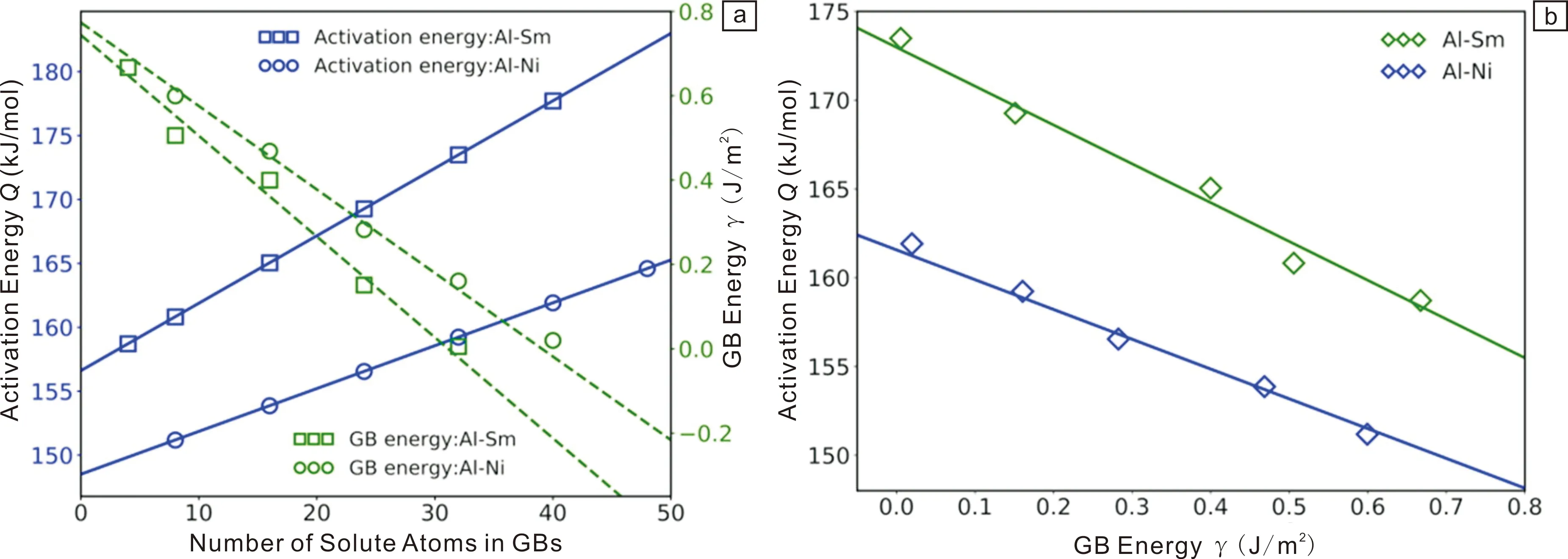
图11 模拟测得晶界能与晶界迁移激活能随着溶质偏析的演化(a)；热动力学相关性模型计算与分子动力学模拟结果(激活能-晶界能)的比较(b)[64]Fig.11 The activation energy as well as the GB energy vs the number of solute atoms in GBs in Al-Ni and Al-Sm (a); The Thero-kinetic correlation model and MD simulations in Al-Sm, the activation energy vs the GB energy in Al-Ni and Al-Sm (b)[64]

因此，溶质偏析将同时导致晶界能的减小和晶界迁移激活能的增大，即同时产生热/动力学稳定性。然而，如果体系温度过高，或者溶质浓度过大，可能析出第二相颗粒或者出现相分离，进而影响体系的热/动力学。如何利用热/动力学相关性，将溶质偏析、第二相析出及相分离效应综合考虑而设计高热稳定性纳米晶材料，已成为该类研究的重要话题。

3.5 基于热/动力学相关性的组织预测

以上分析表明，热力学驱动力和动力学能垒在相变过程中存在关联，而在给定合金和转变条件时，相变的热力学驱动力、动力学能垒和相变组织间也存在关联。针对给定合金，可计算相变过程的有效驱动力和能垒，结合实验分析，得到不同转变条件下热力学驱动力、动力学能垒及相变组织特征间对应关系，即相变的热/动力学相关性；在给定转变条件下，利用该关系可得到转变机制及组织特征，结合相变模型计算得到组织特征参数MPs(microstractural parameters)，即实现终态组织的预测；反之，若已确定目标性能及目标组织，可结合相变的热/动力学相关性及相变模型计算获得目标组织所需的最佳热/动力学条件，并转化为相应的调控工艺参量，实现面向目标组织的调控工艺过程设计及工艺参量优化。

工程合金中微观组织参数(例如尺寸、形状、纵横比和局部结构的空间排列特征)通常由材料加工过程中的相变引起，决定了材料的机械性能，因此具有重要的理论和应用意义。为了正确理解并精确控制相变中的微观组织演变，多年来前人已经提出了各种理论模型(例如解析模型、相场法等来预测微观组织的演化)。但解析模型基于经验性方法，只能描述相竞争的产物类型，不能描述组织演化；相场法侧重于简化的模型体系中耗散模式之间的相互作用，且这类介观演化模型采用唯象的自由能函数，不可避免地忽略了原子尺度物理机理并引入难以确定的模型参数。因此，仍然无法对工程合金加工中的组织演化给出定量结果。

布朗运动是在多个长度/时间尺度上涉及不同互作用的典型过程，在理论上可以通过Langevin方程或等效的Fokker-Planck[65]方程来描述，其中扩散项描述原子尺度上随机且快速变化的相互作用，拖拽项处理粒子的确定性运动。与Langevin方程相比，Fokker-Planck方程使用相空间中的概率密度的非平衡演化来描述粒子的集体运动(collective motion)，避免了跟踪大量原子，是描述结构相变理论的理想方法。从不可逆热力学的角度来看，多个产物的相变过程可以通过非平衡体系的不同耗散路径来表示，每个耗散路径由于特定的转变机制而以不同的速率耗散自由能，因而具有多相竞争的非平衡相变体系演化问题转变为演化路径的选择。最大熵产生原理(maximal entropy production principle)[30, 31]表明非平衡体系演化时在给定的约束下选择特定演化路径，以使熵产生率最大化，因而该原理成为多相竞争体系演化理想的理论工具。

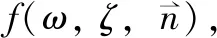
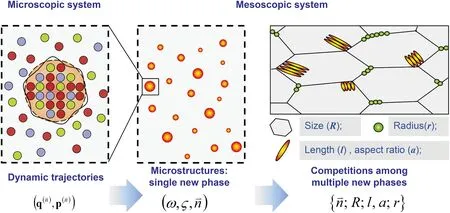
图12 前理论框架中多尺度示意图[28]。左：采用原子位置和动量描述的微观尺度团簇；中：集成变量(包括：体积，界面面积和成分)描述的介观尺度体系；右：典型多相组织竞争时的组织参量Fig.12 Schematic diagram of a multi-scale system with the atomic scale clusters described by positions and momentum of the and the mesoscopic system described by the MPs for RVEs (ω,ζ, and the MPs of typical microstructures R; l, a; r} for the competition among the multiple product phases of different morphologies[28]

(8)

进而采用最大熵产生原理得到介观体系演化的Fokker-Planck方程[28]：

(9)

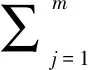
在给定初始分布及转变条件时，通过求解该方程即可解决相变体系从微观到介观的连续演化热/动力学。该模型揭示了组织参量与转变的热/动力学之间的内在联系，应用于Al-Cu合金时效过程的析出问题，在无可调参数的情况下，相对精确地描述了θ″和θ′析出动力学，且得到正确的GP区→θ″→θ′的沉淀序列(图13)[28]；原则上，更复杂的工程合金在各种加工条件下(例如多级温度/变形处理)涉及的相变中，只要选择具体的组织参量(例如尺寸、纵横比等)，并精确地获得每个基本相变阶段的自由能和组织参数相应的速率常数，便可以利用当前模型得到相变体系的演化路径，进而为工程材料加工中微观组织的演化提供一般性的理论框架。

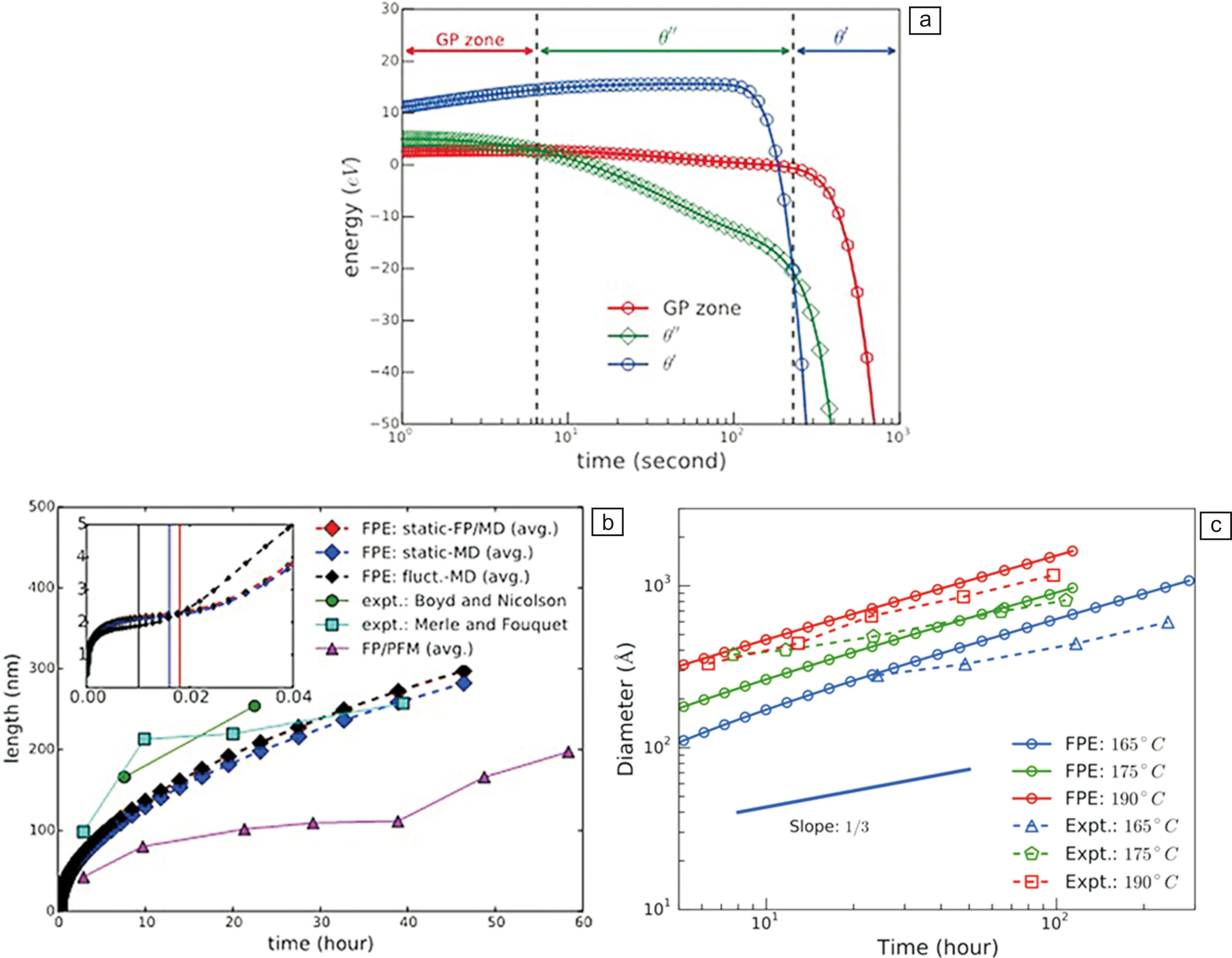
图13 Al-2Cu(原子分数，%)合金相析出过程[28]：(a) GP区、θ″及θ′三相竞争导致的析出次序；(b) θ′尺寸演化与实验结果比较；(c) θ″尺寸演化与实验结果比较Fig.13 The calculated precipitation sequence in Al-2at%Cu alloy at 473 K from the current model[28]. Note that the well-established precipitation sequence of GP zone→θ″→θ′ is predicted (a); The size evolution of θ′ precipitates, the experiments of Merle and Fouquet, as well as the calculations of Vaithyanathan et al. due to combined FP (first-principles) calculations and phase field method (FP/PFM), are shown for comparison(b); The size evolution of θ″ precipitates at various temperatures, the experiments of Merle and Fouquet are shown for comparison(c)

4 结 语

大量的实验及理论结果一致表明[66-71]，在体系自发演化中，随热力学驱动力增大(减小)，体系转变的能垒减小(增大)；反之亦然。由于热/动力学相关性通过驱动力、能垒将相变条件与组织特征联系起来，形成工艺条件-相变理论-组织性能间的逻辑闭环，因而，必将为非平衡相变组织预测和工艺设计带来新理念和创新性发展。

热/动力学协同作为中轴贯通加工工艺、微观组织以及力学性能，而如何描述这种协同，需要求助于耦合成分/工艺及微观组织集成变量的非平衡组织演化多尺度模型，其精髓在于：随相变条件变化，最简单、最直接、最能表达物理真情实感的模型应不必区分形核与长大，不必区分具体相变机理，也不必关注不同的时间和空间尺度，其真正中枢是热力学驱动力、动力学能垒和终态微观组织间关联。究其根本，材料加工工艺的确定应该面向目标组织和性能。将以关键组织性能为目标定量化设计材料成分及加工工艺的思路应用于材料设计中，不仅可提高设计效率、降低成本，并且可推动合金成分及加工工艺设计由经验性模式向定量化模式转变。结合大量文献报道[72-75]，作者课题组归纳得到，相变发生时的能量状态大小对应相变产物即组织的强度高低，而相变发生快慢对应组织塑性大小。这种对应纯属偶然还是有其物理根源？作者课题组理解，热力学驱动力和动力学能垒有相关性(互斥)，驱动力、能垒同微观组织间亦存在关联，而微观组织决定材料性能，所以，相变驱动力/能垒间互斥与材料强度/塑性间互斥很可能存在关联。如果定量证实，设计大驱动力和大能垒的关键相变会导致终态组织同时获取大强度和大塑性，将引发材料加工理论及技术的革命性发展，也就是说，以定量决定材料性能为目的的成分及加工工艺设计。

相变热力学驱动力和动力学能垒间不同的互斥组合体现出加工工艺的变化，决定了微观组织的不同，进而决定关键力学性能的不同，这种不同是否体现于强韧性的不同互斥组合，是否对应于加工硬化中位错组态演化(运动、增殖及位错与微观缺陷交互作用)的热力学和动力学，非常值得深入探究。探究强韧化机制的共性根本，可以构建位错组态演化与材料力学性能间的关联。可见，材料加工涉及相变的热/动力学同加工硬化涉及位错组态演化的热/动力学间的理论关联，至关重要。这里面涉及3个关键问题：大驱动力大能垒组合得到的相变组织的弹性模量如何计算或测量？相变的大驱动力和大能垒同屈服前组织内位错存储以及屈服后加工硬化的关联？如何根据达到抗拉强度时位错组态同屈服开始时位错组态的区别，来得到强度和塑性的演化？解决上述问题，便可以真正实现热/动力学协同定量贯通加工工艺-微观组织-力学性能。