马氏田口施密特度量学习算法研究
郑 锐,刘久富 ,杨 忠,王志胜,刘海阳,丁晓彬
(1.南京航空航天大学 自动化学院,江苏 南京 211100;2.东南大学 电子科学与工程学院,江苏 南京 210096)
0 引 言
睡眠质量问题一直是人们关注自身健康和科学研究的重点之一,有效地区分睡眠质量的高低对于治疗睡眠呼吸暂停,失眠和发作性睡病十分有益。以往,人们对睡眠质量的检测基本是依靠人自身的主观感受,医学专家只有通过病人口述症状和结合其他并发症状才能判断出病人的睡眠情况,这种方法缺乏客观性,过程繁琐,准确性不高。睡眠研究的重要数据人体脑电信(electroencephalogram,EEG)数据量巨大,人工通过实验观察存在较大的复杂性。计算生物学上常应用统计学和计算机算法对复杂海量的生物学信号进行识别和处理,可以有效地提取有用的信息[1]。文中引入了睡眠专家标注过的六状态睡眠分期脑电信号进行分析。
马氏田口方法作为一种模式识别与分类方法,广泛应用于多元系统的自动化异常诊断与分析中,准确性较好[2-3]。通过构建马氏基准空间,可以有效地区分正常样本和异常样本。通过正交表和信噪比来对各个变量进行优化,选取最优的变量从而对所研究的问题进行更好的分类和预测[4]。文中在人工专家睡眠分期标记过的脑电信号数据的基础上,采用施密特正交化马氏田口方法(Mahalanobis-Taguchi-Gram-Schmidt process,MTGS)对人睡眠质量的正常和异常进行检测。与传统的马氏田口方法(Mahalanobis-Taguchi system,MTS)需要计算相关矩阵的逆矩阵不同,该方法通过施密特正交化计算马氏距离,能够有效地处理多重共线性问题,不必通过正交表计算信噪比,降低了算法的运算复杂度。
1 马氏田口施密特正交化法
1.1 马氏田口系统
MTGS比MTS具有更大的优势,为了突出显示这些方法之间的差异,先阐述一下MTS,之后将讨论MTGS及其改进的变体。
在马氏田口系统中计算马氏距离(Mahalanobis-distance,MD)可参见下列公式[5-6]:
(1)
Zij=(Xij-mi)/si
(2)
其中,i(i=1,2,…,k)表示变量数目,k表示变量总数;j(j=1,2,…,n)表示样本数目,n表示样本总数;Zij表示归一化变量Xij的标准化向量,Xij表示第j个样本的第i个变量值;mi表示健康组中的第i个变量的平均值;si表示健康组中第i个变量的标准偏差;C表示健康组的关联矩阵。
在计算马氏距离(MD)之后,使用正交阵列来计算每个实验的信噪比S/N。在正交阵列中,考虑了两个级别的变量,这表明它们的存在或不存在。根据用于构建MD的变量,确定信噪比S/N的类型。对于真实水平异常未知的制造检验,信噪比S/N越大越好[7]。信噪比S/N可以用以下方式计算:
(3)
在式1中,对于所考虑的变量之间存在相关性非常高的情况,相关矩阵变得奇异,相关矩阵C的逆矩阵不正确。这种在变量之间具有强相关性的现象称为多重共线性,根据式1和式2,可能不准确。此外,在某些情况下需要观察到良好的异常值发生方向,MTS无法识别异常的方向,对于异常方向的多重共线性和识别,优选MTGS方法。
1.2 马氏田口正交化方法
MTGS是对MTS的改进,通过Gram-Schmidt正交化处理(Gram-Schmidt orthogonalization process,GSP)可以计算出MTGS方法中的MD。
Gram-Schmidt正交化处理将线性独立向量转换成正交向量。通过式2得到的正态变量(Zij)的标准化向量被视为线性独立向量以计算向量的正交集合。Gram-Schmidt正交化过程的方程组如下[8-9]:
(4)
其中,Zk=(Zk1,Zk2,…,Zkn)是根据等式获得的标准矢量的第k组;Uk=(Uk1,Uk2,…,Ukn)是具有相同线性跨度的相互垂直向量的第k组。
对应第j次观测的马氏距离如下式[10]:
(5)
其中,Ukj是正交矢量Uk的元素;Sk是Uk的标准偏差;k是变量总数。
在MTGS方法中,可以直接计算变量的S/N比。第i个变量的信噪比S/N[11]为:
(6)
然而,根据式6计算S/N,只有当所考虑的变量之间的部分相关性的影响不显著时才有效。另外,通过利用式6在MTGS过程中,结果取决于考虑变量的顺序。因此,通过MTGS方法计算MD并采用正交阵列,并根据式3评估S/N比的方法消除了MTS和MTGS的所有缺点。这里使用改进过的MTGS方法。
1.3 异常检测算法
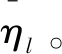
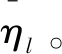
算法:MTGS异常检测算法
输入:Xij,M,N;
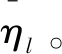
1.获取数据序列Xij。
3.求解归一化向量Zij。
While(1≤i≤M)
While(1≤i≤N)
Zij=(Xij-mi)/si
End While;
End While;
ReturnZij
4.施密特正交化处理,得到Uij。
While(1≤k≤M)
End While;
ReturnU1,U2,…,Uk
5.求解Uk的标准差si,Uij为Uk中的元素。
6.计算信噪比值ηi。
While(1≤j≤N)
While(1≤i≤M)
ηi=-10*log(Si*Si/Uji*Uji)
End While;
End While;
Returnηi
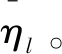
While(1≤j≤N)
x=x+ηi
End While;
2 睡眠建模分析及实验数据处理
多导睡眠图是一种应用于睡眠障碍诊断和治疗的技术,其中脑电信号(EEG)是代表大脑神经元活动的一种电信号,可无创测量,所以EEG信号一直是研究人体不同睡眠周期大脑活动的有力工具[12]。传统的睡眠阶段分类是专家根据Rechtschaffen和Kales(R & K)制定的分类标准。文中使用R & K标准中的六状态睡眠阶段:清醒期(Awa),第1阶段(S1),第2阶段(S2),第3阶段(S3),第4阶段(S4)和快速眼动期(REM)。
2.1 实验数据
使用的实验数据来自Sleep-EDF数据库,它是Physionet数据库的一部分。文中使用了两组实测的睡眠脑电数据记录,测试者的年龄为21~55岁,平均年龄36岁。第一组数据记录了112例睡眠健康志愿者的睡眠数据,把这一组作为研究的睡眠正常组。第二组数据记录了108例有轻度睡眠障碍的受试者的睡眠数据,把这一组作为研究的睡眠异常组。在这项研究中,选择Pz-Oz和Fpz-Cz两个通道的EEG信号来分析和识别睡眠阶段。这些段的原始睡眠阶段用6个类别来标记:S1,S2,S3,S4,REM和Awa,文中研究仅涉及AWA,S1~S4和REM睡眠阶段。对每个通道的每个睡眠阶段分别采样,两个通道的六个周期各采集200组EEG信号值,EEG信号图如图1所示。

图1 EEG信号
2.2 数据处理与分析
采用前述的GSP方法对睡眠数据进行处理。MTGS异常检测算法展示了数据处理的全过程,健康组样本和异常组样本均采用该算法。
利用六个周期的健康组和异常组样本数据,计算出各个通道的均值mi、标准差si。然后根据式2对原始向量进行标准化处理以得到线性独立向量,对线性独立向量做正交化处理。使用式6计算出各样本的S/N信噪比值。分别求取健康组和异常组六个睡眠周期的S/N比率的平均值,绘制健康组与异常组S/N信噪比平均值分布的波形图,如图2所示。
可以看出,从清醒期开始,第一阶段到第四阶段,再到REM阶段,睡眠正常者的各周期信噪比均值均处于睡眠异常者的上方,由此看来,可以明显区分出睡眠正常者和睡眠异常者。
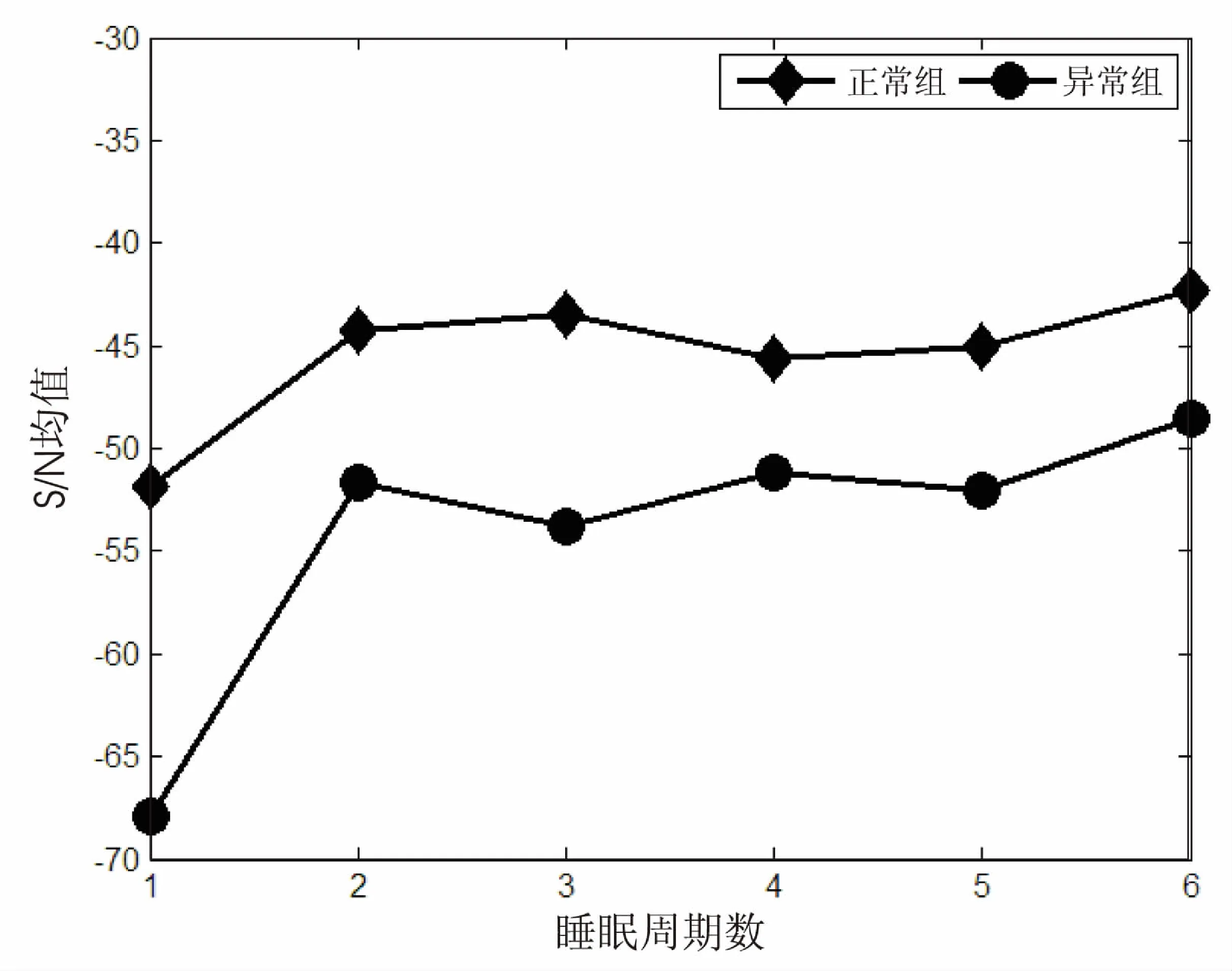
图2 S/N均值波形
图中,睡眠异常者的清醒期的信噪比均值与睡眠正常者相比,差距很大,进入睡眠第一阶段后有一个明显的提升。相较于睡眠正常者,异常者的六个睡眠周期的信噪比均值的波动性较大。此外,两条信噪比均值的曲线都呈上升趋势,其中异常者的上升幅度明显快于正常者。
在清醒期(Awa),睡眠正常者和异常者信噪比均值分别为-51.84和-67.94,二者差值达到了16.1,差距很大。在睡眠周期的第一阶段,睡眠正常者信噪比均值为-44.22,睡眠异常者信噪比均值为-51.62,比健康者降低了7.4,相较于清醒期差值有所减小;第二阶段相较于第一阶段二者的差距有所拉大;第三阶段,睡眠正常者的信噪比均值为-45.64,睡眠异常者的信噪比均值为-51.13,异常者要比正常者低了5.49,信噪比均值的差距缩小,但仍大于第一阶段的差距;第四阶段,睡眠异常者要比正常者低了7.0,相较于上一阶段差距增大;在REM阶段,睡眠正常者与异常者的差值达到6.21,比上一阶段有小幅减少。
3 结束语
阐述了人体睡眠质量的自动检测方法,采用施密特正交化马氏田口方法求取EEG信号的信噪比均值,进而实现对正常者和异常者的有效辨识。采用的EEG信号由人工专家精确划分为六个睡眠周期,分别对这六个睡眠周期使用马氏田口正交化处理方法(MTGS)求取信噪比值。最后对各个周期的信噪比均值波形进行对照发现,从清醒期开始,第一阶段到第四阶段,再到REM阶段,睡眠正常者的各周期信噪比均值均处于睡眠异常者的上方。因此,使用MTGS方法可以有效地区分睡眠正常者和睡眠异常者。将该算法应用于人体睡眠质量判别,为人工智能自动检测睡眠质量取代传统人工判别提供了新的思路。
将马氏田口模型应用于解决人体睡眠质量的检测问题,有一定的可行性,但考虑其实现的前提是要基于人工专家划分完成的六个睡眠分期,使其应用存在局限性。未来可考虑采用马氏田口模型对睡眠脑电信号进行自动睡眠分期,从而提升整体睡眠质量检测算法的应用范围。

